Запятая (музыка)

Очень маленький интервал, возникающий из-за расхождений в настройке

В теории музыки запятая — это очень маленький интервал , разница, возникающая в результате настройки одной ноты двумя разными способами. ^[1] Традиционно существует две наиболее распространённые запятые: синтоническая запятая , «разница между одной большой терцией и четырьмя чистыми квинтами за вычетом двух октав», и пифагорейская запятая , «разница между двенадцатью квинтами и семью октавами». ^[2] Слово запятая, используемое без уточнения, относится к синтонической запятой , ^[3] которую можно определить, например, как разницу между F ♯, настроенной с использованием пифагорейской системы настройки , основанной на ре , и другой F ♯, настроенной с использованием системы настройки четверть-запятая, основанной на ре . Интервалы, разделённые соотношением 81:80, считаются одной и той же нотой, поскольку 12-нотная западная хроматическая гамма не отличает пифагорейские интервалы от 5-предельных интервалов в своей нотации. Другие интервалы считаются запятыми из-за энгармонических эквивалентностей системы настройки. Например, в 53TET , B ♭ и A ♯ оба приближены к одному и тому же интервалу, хотя они отстоят друг от друга на семеричную клеизму .

Этимология

Переводя в этом контексте, «запятая» означает «волосок», как в «off by just a hair» ^{[ требуется цитата ]} . Слово «запятая» пришло через латынь от греческого κόμμα , от более раннего * $κοπ-μα$ : «результат или эффект разрезания».

Описание

В одной и той же системе настройки две энгармонически эквивалентные ноты (например, G ♯ и A ♭ ) могут иметь немного разную частоту, а интервал между ними — комма. Например, в расширенных гаммах, созданных с пятипредельной настройкой, A ♭, настроенная как большая терция ниже C ₅ , и G ♯, настроенная как две большие терции выше C _4, не являются в точности одной и той же нотой, как если бы они были в равномерной темперации . Интервал между этими нотами, диеза , — это легко слышимая комма (ее размер составляет более 40% полутона ) .

Запятые часто определяются как разница в размере между двумя полутонами. ^{[ необходима цитата ]} Каждая система настройки темперации мезонита производит 12-тоновую шкалу, характеризующуюся двумя различными видами полутонов (диатоническими и хроматическими), и, следовательно, запятой уникального размера. То же самое верно и для пифагорейской настройки.

В простом интонировании может быть получено более двух видов полутонов. Таким образом, одна система настройки может характеризоваться несколькими различными коммами. Например, обычно используемая версия пятипредельной настройки производит 12-тоновую шкалу с четырьмя видами полутонов и четырьмя коммами .

Размер запятых обычно выражается и сравнивается в центах — 1 ⁄ 1200 долях октавы по логарифмической шкале .

Запятые в разных контекстах

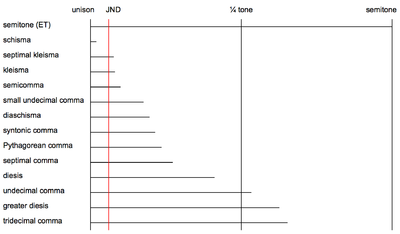
В столбце ниже, озаглавленном «Разница между полутонами », min 2 — малая секунда (диатонический полутон), ^aug 1 — увеличенный унисон (хроматический полутон), а S ₁ , S ₂ , S ₃ , S ₄ — полутоны, как определено здесь . В столбцах, озаглавленных « Интервал 1» и «Интервал 2», все интервалы предположительно настроены только на интонацию . Обратите внимание, что пифагорейская комма ( $κ$ _𝜋 ) и синтоническая комма ( $κ$ _S ) — это основные интервалы, которые можно использовать в качестве мерил для определения некоторых других комм. Например, разница между ними — это маленькая запятая, называемая схизма . Схизма не слышна во многих контекстах, так как ее размер уже, чем наименьшая слышимая разница между тонами (которая составляет около шести центов, также известная как едва заметная разница , или JND).

Имя запятой	Альтернативное название	Определения				Размер
		Разница между полутонами	Разница между запятыми	Разница между		Центы	Соотношение
		Разница между полутонами	Разница между запятыми	Интервал 1	Интервал 2	Центы	Соотношение
раскол	схизма	^авг 1 − мин 2 в ⁠ 1 /12⁠ запятая означала один	1 $κ$ _𝜋 − 1 $κ$ _S	8 чистых квинт + 1 большая терция	5 октав	1.95	${\tfrac {\ 32805\ }{32768}}$
септальная клеизма				3 основные терции	1 октава − 1 септимальная запятая	7.71	${\tfrac {\ 225\ }{224}}$
клеизма				6 малых терций	1 октава + 1 чистая квинта (« тритава »)	8.11	${\tfrac {\ 15625\ }{15552}}$
маленькая недесятичная запятая ^[4]				1 нейтральная секунда	1 минорный тон	17.40	${\tfrac {\ 100\ }{99}}$
диасхизма	диасхизма	мин 2 − ^авг 1 в ⁠ 1 /6⁠ запятая означает один, S₃ − S₂ в настройке 5-го предела	2 $κ$ _S − 1 $κ$ _𝜋	3 октавы	4 чистых квинты + 2 большие терции	19.55	${\tfrac {\ 2048\ }{2025}}$
синтоническая запятая ( $κ$ _S )	Запятая Дидима	S ₂ − S ₁ в 5 предельная настройка		4 чистых квинты	2 октавы + 1 большая терция	21.51	${\tfrac {\ 81\ }{80}}$
синтоническая запятая ( $κ$ _S )	Запятая Дидима	S ₂ − S ₁ в 5 предельная настройка		мажорный тон	минорный тон	21.51	${\tfrac {\ 81\ }{80}}$
53 ТЕТ запятая ( $κ$ ₅₃ )	1 шаг (в 53 ТЕТ )	⁠ 1 /9⁠ мажорный тон (в 53 ТЕТ )	⁠ 1 /8⁠ минорный тон (в 53 ТЕТ )	мажорный тон (в 53 ТЕТ )	минорный тон (в 53 ТЕТ )	22.64	${\bigl (}2{\bigr )}^{\tfrac {\ 1\ }{53}}$
Пифагорейская запятая ( $κ$ _𝜋 )	дитоническая запятая	^авг 1 − мин 2 (в пифагорейском строе )		12 чистых квинт	7 октав	23.46	${\tfrac {\ 531441\ }{524288}}$
семеричная запятая ^[5]	Запятая Архита ( $κ$ _А )			малая септаккорд	септимальная малая септима	27.26	${\tfrac {\ 64\ }{63}}$
диезис	малый диезис уменьшился второй	мин 2 − ^авг 1 в ⁠ 1 /4⁠ запятая означает один, S₃− S₁ в 5 предельная настройка	3 $κ$ _S − 1 $κ$ _𝜋	октава	3 основные терции	41.06	${\tfrac {\ 128\ }{125}}$
недесятичная запятая ^[5]^[6]	Одиннадцатеричная четверть тона			одиннадцатеричный тритон	идеальная четвертая	53.27	${\tfrac {\ 33\ }{32}}$
большая диеза		мин 2 − ^авг 1 в ⁠ 1 /3⁠ запятая означает один, S₄ − S₁ в 5 предельная настройка	4 $κ$ _S − 1 $κ$ _𝜋	4 малые терции	октава	62.57	${\tfrac {\ 648\ }{625}}$
трехзначная запятая	тридецимальный третий тон			тридецимальный тритон	идеальная четвертая	65.34	${\tfrac {\ 27\ }{26}}$

Многие другие запятые были перечислены и названы микротоналистами. ^[7]

Синтоническая комма играет решающую роль в истории музыки. Это величина, на которую некоторые ноты, произведенные в пифагорейской настройке, были сглажены или заострены, чтобы произвести только малые и большие терции. В пифагорейской настройке единственными высококонсонантными интервалами были чистая квинта и ее обращение, чистая кварта . Пифагорейская большая терция (81:64) и малая терция (32:27) были диссонантными , и это мешало музыкантам свободно использовать трезвучия и аккорды , заставляя их писать музыку с относительно простой текстурой . Музыканты в позднем Средневековье осознали, что, слегка смягчив высоту некоторых нот, пифагорейские терции можно сделать консонантными . Например, если вы уменьшите частоту E с помощью синтонической коммы (81:80), C–E (большая терция) и E–G (малая терция) станут просто: C–E сглажено до простого соотношения

{\frac {\ 81\ }{64}}\cdot {\frac {\ 80\ }{81}}={\frac {\ 1\cdot 5\ }{4\cdot 1}}={\frac {\ 5\ }{4}}

и в то же время E–G заостряется до справедливого соотношения

{\frac {32}{\ 27\ }}\cdot {\frac {81}{\ 80\ }}={\frac {2\cdot 3}{\ 1\cdot 5\ }}={\frac {6}{\ 5\ }}

Это привело к созданию новой системы настройки , известной как четвертная комма meantone , которая позволила полностью развить музыку со сложной текстурой , такую как полифоническая музыка или мелодии с инструментальным сопровождением . С тех пор были разработаны другие системы настройки, и синтоническая комма использовалась в качестве опорного значения для темперирования чистых квинт во всем семействе синтонических темпераций , включая meantone .

Альтернативные определения

В четвертной запятой и любой системе настройки темперации с запятой, которая темперирует квинту до размера менее 700 центов, запятая является уменьшенной секундой , которую можно эквивалентно определить как разницу между:

малая секунда и увеличенный унисон (также известный как диатонические и хроматические полутоны ), или
большая секунда и уменьшенная терция , или
малая терция и увеличенная секунда , или
большая терция и уменьшенная кварта , или
чистая кварта и увеличенная терция , или
увеличенная кварта и уменьшенная квинта , или
чистая квинта и уменьшенная секста , или
малая секста и увеличенная квинта , или
большая секста и уменьшенная септаккорда , или
малая септима и увеличенная секста , или
большая септаккорда и уменьшенная октава .

В пифагорейской настройке и любой системе настройки темперации среднего тона, которая темперирует квинту до размера, превышающего 700 центов (например , ⁠ 1 /12⁠ comma meanone), комма является противоположностью уменьшенной секунды, и, следовательно, противоположностью вышеперечисленных различий. Точнее, в этих системах настройки уменьшенная секунда является нисходящим интервалом, тогда как комма является ее восходящей противоположностью. Например, пифагорейская комма (531441:524288, или около 23,5 центов) может быть вычислена как разница между хроматическим и диатоническим полутоном, что является противоположностью пифагорейской уменьшенной секунды (524288:531441, или около −23,5 центов).

В каждой из вышеперечисленных систем настройки все вышеперечисленные различия имеют одинаковый размер. Например, в пифагорейской настройке они все равны противоположности пифагорейской коммы , а в четвертной комме meanone они все равны диесе .

Обозначение

В 2000–2004 годах Марк Сабат и Вольфганг фон Швайниц работали вместе в Берлине над разработкой метода точного указания высоты тона в нотной записи. Этот метод был назван расширенной нотной записью Гельмгольца-Эллиса JI . ^[8] Сабат и Швайниц берут «обычные» бемоли, бекари и диезы как пифагорейский ряд чистых квинт. Таким образом, ряд чистых квинт, начинающийся с F, продолжается CGDAEBF ♯ и так далее. Преимущество для музыкантов заключается в том, что традиционное прочтение основных кварт и квинт остается привычным. Такой подход также пропагандировали Дэниел Джеймс Вольф и Джо Монзо, который называет его аббревиатурой HEWM (Гельмгольц-Эллис-Вольф-Монзо). ^[9] В дизайне Сабата-Швайница синтонические запятые обозначены стрелками, прикрепленными к бемольному, натуральному или диезному знаку, септальные запятые — символом Джузеппе Тартини, а недесятичные четвертьтоны — общепринятыми знаками четвертитона (один крест и бемоль в обратном порядке ). Для более высоких штрихов были разработаны дополнительные знаки. Для облегчения быстрой оценки высоты тона могут быть добавлены центы (отклонения вниз ниже и отклонения вверх выше соответствующей случайности). Используемое соглашение заключается в том, что написанные центы относятся к темперированной высоте тона, подразумеваемой знаком бемоль, натурального или диезного знака и названием ноты. Одним из больших преимуществ любой такой нотации является то, что она позволяет точно записывать натуральный гармонический ряд. Полная легенда и шрифты для нотации (см. примеры) являются открытым исходным кодом и доступны в Plainsound Music Edition. ^{[ необходима полная цитата ]} Таким образом, пифагорейская гамма — это CDEFGABC , в то время как простая гамма — это CDE FGA Б С .

Композитор Бен Джонстон использует «−» в качестве знака альтерации, чтобы указать, что нота понижена синтонической запятой, или «+», чтобы указать, что нота повышена синтонической запятой; ^[10] однако «базовая гамма» Джонстона (простые номиналы ABCDEFG ) настроена на просто интонацию и, таким образом, уже включает в себя синтоническую запятую. Таким образом, пифагорейская гамма — это CD E+ FG A+ B+ C , в то время как простая гамма — это CDEFGAB .

Темперирование запятых

Запятые часто используются при описании музыкальных темпераций , где они описывают различия между музыкальными интервалами, которые устраняются этой системой настройки. Запятую можно рассматривать как расстояние между двумя музыкальными интервалами. Когда заданная запятая темперируется в системе настройки, способность различать эти два интервала в этой настройке устраняется. Например, разница между диатоническим полутоном и хроматическим полутоном называется диезисом. Широко используемая 12-тоновая равномерная темперация темперирует диезис и, таким образом, не различает два разных типа полутонов. С другой стороны, 19-тоновая равномерная темперация не темперирует эту запятую и, таким образом, различает два полутона.

Примеры:

12 ТЕТ смягчает диезу, а также ряд других запятых.
19 TET смягчает септальный диезис и синтоническую запятую , но не смягчает диезис.
22 TET смягчает септальную запятую Архита , но не смягчает септальную диезу или синтоническую запятую.
31 TET смягчает синтоническую запятую, а также запятую, определяемую соотношением ⁠ 99 /98⁠ , но не смягчает диезу, семеричную диезу или семеричную запятую Архита.

В следующей таблице перечислено количество используемых шагов, которые соответствуют различным точным интервалам в различных системах настройки. Нули указывают, что интервал является запятой (т.е. темперирован) в данной конкретной равномерной темперации. ^{[ необходимо пояснение ]} Все соотношения частот в первом столбце связаны со статьей в Википедии.

Интервал (частотное отношение)	5 Т ЭДО	7 Т ЭДО	12 Т ЭДО	19 Т ЭДО	22 Т ЭДО	31 Т ЭДО	34 Т ЭДО	41 Т ЭДО	53 Т ЭДО	72 Т ЭДО
${\tfrac {\ 2\ }{1}}$	5	7	12	19	22	31	34	41	53	72
${\tfrac {\ 15\ }{8}}$	5	6	11	17	20	28	31	37	48	65
${\tfrac {\ 9\ }{5}}$	4	6	10	16	19	26	29	35	45	61
${\tfrac {\ 7\ }{4}}$	4	6	10	15	18	25	28	33	43	58
${\tfrac {\ 5\ }{3}}$	4	5	9	14	16	23	25	30	39	53
${\tfrac {\ 8\ }{5}}$	3	5	8	13	15	21	23	28	36	49
${\tfrac {\ 3\ }{2}}$	3	4	7	11	13	18	20	24	31	42
${\tfrac {\ 10\ }{7}}$	3	3	6	10	11	16	17	21	27	37
${\tfrac {\ 64\ }{45}}$	2	4	6	10	11	16	17	21	27	37
${\tfrac {\ 45\ }{32}}$	3	3	6	9	11	15	17	20	26	35
${\tfrac {\ 7\ }{5}}$	2	4	6	9	11	15	17	20	26	35
${\tfrac {\ 4\ }{3}}$	2	3	5	8	9	13	14	17	22	30
${\tfrac {\ 9\ }{7}}$	2	2	4	7	8	11	12	15	19	26
${\tfrac {\ 5\ }{4}}$	2	2	4	6	7	10	11	13	17	23
${\tfrac {\ 6\ }{5}}$	1	2	3	5	6	8	9	11	14	19
${\tfrac {\ 7\ }{6}}$	1	2	3	4	5	7	8	9	12	16
${\tfrac {\ 8\ }{7}}$	1	1	2	4	4	6	6	8	10	14
${\tfrac {\ 9\ }{8}}$	1	1	2	3	4	5	6	7	9	12
${\tfrac {\ 10\ }{9}}$	1	1	2	3	3	5	5	6	8	11
${\tfrac {\ 27\ }{25}}$	0	1	1	2	3	3	4	5	6	8
${\tfrac {\ 15\ }{14}}$	1	0	1	2	2	3	3	4	5	7
${\tfrac {\ 16\ }{15}}$	0	1	1	2	2	3	3	4	5	7
${\tfrac {\ 21\ }{20}}$	0	1	1	1	2	2	3	3	4	5
${\tfrac {\ 25\ }{24}}$	1	0	1	1	1	2	2	2	3	4
${\tfrac {\ 648\ }{625}}$	−1	1	0	1	2	1	2	3	3	4
${\tfrac {\ 28\ }{27}}$	0	1	1	1	1	2	2	2	3	4
${\tfrac {\ 36\ }{35}}$	0	0	0	1	1	1	1	2	2	3
${\tfrac {\ 128\ }{125}}$	−1	1	0	1	1	1	1	2	2	3
${\tfrac {\ 49\ }{48}}$	0	1	1	0	1	1	2	1	2	2
${\tfrac {\ 50\ }{49}}$	1	−1	0	1	0	1	0	1	1	2
${\tfrac {\ 64\ }{63}}$	0	0	0	1	0	1	0	1	1	2
${\tfrac {\ 531441\ }{524288}}$	1	−1	0	−1	2	−1	2	1	1	0
${\tfrac {\ 81\ }{80}}$	0	0	0	0	1	0	1	1	1	1
${\tfrac {\ 2048\ }{2025}}$	−1	1	0	1	0	1	0	1	1	2
${\tfrac {\ 126\ }{125}}$	−1	1	0	0	1	0	1	1	1	1
${\tfrac {\ 1728\ }{1715}}$	0	−1	−1	1	0	0	−1	1	0	1
${\tfrac {\ 2109375\ }{2097152}}$	3	−2	1	−1	0	0	1	−1	0	−1
${\tfrac {\ 15625\ }{15552}}$	2	−1	1	0	−1	1	0	−1	0	0
${\tfrac {\ 225\ }{224}}$	1	−1	0	0	0	0	0	0	0	0
${\tfrac {\ 32805\ }{32768}}$	1	−1	0	−1	1	−1	1	0	0	−1
${\tfrac {\ 2401\ }{2400}}$	−1	2	1	−1	1	0	2	0	1	0
${\tfrac {\ 4375\ }{4374}}$	−1	0	−1	0	1	−1	0	1	0	0

Комма также может рассматриваться как дробный интервал, который остается после "полного круга" некоторого повторяющегося выбранного интервала; повторяющиеся интервалы имеют одинаковый размер по относительной высоте, и все производимые тоны уменьшаются или повышаются на целые октавы обратно к октаве, окружающей начальную высоту. Пифагорейская комма, например, это разница, полученная, скажем, между A ♭ и G ♯ после круга из двенадцати только квинт. Круг из трех только больших терций, такой как A ♭ CEG ♯ , дает малый диезис ⁠ 128 /125⁠ (41,1 цент ) между G ♯ и A ♭ . Круг из четырех только малых терций, например G ♯ BDFA ♭ , дает интервал ⁠ 648 /625⁠ между A ♭ и G ♯ и т. д. Интересное свойство темпераций состоит в том, что эта разница сохраняется независимо от настройки интервалов, образующих круг. ^[11] В этом смысле запятые и подобные минутные интервалы никогда не могут быть полностью темперированы, независимо от настройки.

Последовательность запятых

Последовательность запятых определяет музыкальную темперацию посредством уникальной последовательности запятых в возрастающих простых пределах . ^[12] Первая запятая в последовательности запятых находится в $q$ -пределе, где $q$ - $n$ -ое нечетное простое число (простое число 2 игнорируется, поскольку оно представляет октаву), а $n$ - число генераторов . Последующие запятые находятся в простых пределах, каждое из которых является следующим простым числом в последовательности выше предыдущего.

Другие интервалы, называемые запятыми

Есть также несколько интервалов, называемых запятыми, которые технически не являются запятыми, потому что они не являются рациональными дробями, как те, что выше, но являются иррациональными приближениями к ним. К ним относятся запятые Холдриана и Меркатора, ^[13] и размер шага от шага к шагу в 53 TET .

Смотрите также

Ссылки

↑ Уолдо Селден Пратт (1922). Словарь музыки и музыкантов Гроува , т. 1, стр. 568. Джон Александр Фуллер Мейтленд , сэр Джордж Гроув , ред. Macmillan.
^ Клайв Грейтед (2001). "Comma", Grove Music Online . doi :10.1093/gmo/9781561592630.article.06186
^ Бенсон, Дэйв (2006). Музыка: Математическое предложение , стр. 171. ISBN 0-521-85387-7 .
^ Халушка, Ян (2003). Математическая теория тоновых систем . CRC Press. стр. $xxvi$ . ISBN 0-8247-4714-3.
^ ab Rasch, Rudolph (2000). "Пару слов о настройках Гарри Парча". В Dunn, David (ред.). Гарри Парч: Антология критических взглядов . стр. 34. ISBN 90-5755-065-2.— Описывает разницу между 11 предельными и 3 предельными интервалами.
^ Раш, Рудольф (1988). «Системы музыкальной интонации Фэри». В Benitez, JM; et al. (ред.). Listening . Vol. 2. p. 40. ISBN 3-7186-4846-6.= Источник для 32:33 как разница между 11:16 и 2:3.
^ "Список запятых, по пределу простых чисел". Xenharmonic wiki .
^ см. статью «Расширенная нотация высоты звука Гельмгольца-Эллиса JI: eine Notationsmetode für dienatürlichen Intervalle» в Mikrotöne und mehr – Auf György Ligetis Hamburger Pfaden , изд. Манфред Станке , фон Бокель Верлаг, Гамбург, 2005 г., ISBN 3-932696-62-X
^ Статья в Tonalsoft Encyclopaedia о нотации «HEWM»
^ Джон Фонвилл . «Расширенная четкая интонация Бена Джонстона – руководство для интерпретаторов», стр. 109, «Перспективы новой музыки » , т. 29, № 2 (лето 1991 г.), стр. 106–137. и Джонстон, Бен и Гилмор, Боб (2006). «Система нотации для расширенной четкой интонации» (2003), «Максимальная ясность» и другие сочинения о музыке , стр. 78. ISBN 978-0-252-03098-7
^ Раш, Рудольф (2002). «Настройка и темперация». В Кристенсене, Т. (ред.). Кембриджская история западной музыкальной теории . Cambridge University Press. стр. 201. ISBN 0-521-62371-5.
^ Смит, GW "Comma sequences". Xenharmony . Получено 26 июля 2012 г. – через lumma.org.
^ Монзо, Джо. «Запятая Меркатора / Запятая Меркатора». tonalsoft.com .

[1] Уолдо Селден Пратт (1922). Словарь музыки и музыкантов Гроува , т. 1, стр. 568. Джон Александр Фуллер Мейтленд , сэр Джордж Гроув , ред. Macmillan.

[2] Клайв Грейтед (2001). "Comma", Grove Music Online . doi :10.1093/gmo/9781561592630.article.06186

[3] Бенсон, Дэйв (2006). Музыка: Математическое предложение , стр. 171. ISBN 0-521-85387-7 .

[4] Халушка, Ян (2003). Математическая теория тоновых систем . CRC Press. стр. $xxvi$ . ISBN 0-8247-4714-3.

[Rasch-5] Rasch, Rudolph (2000). "Пару слов о настройках Гарри Парча". В Dunn, David (ред.). Гарри Парч: Антология критических взглядов . стр. 34. ISBN 90-5755-065-2.— Описывает разницу между 11 предельными и 3 предельными интервалами.

[6] Раш, Рудольф (1988). «Системы музыкальной интонации Фэри». В Benitez, JM; et al. (ред.). Listening . Vol. 2. p. 40. ISBN 3-7186-4846-6.= Источник для 32:33 как разница между 11:16 и 2:3.

[7] "Список запятых, по пределу простых чисел". Xenharmonic wiki .

[8] см. статью «Расширенная нотация высоты звука Гельмгольца-Эллиса JI: eine Notationsmetode für dienatürlichen Intervalle» в Mikrotöne und mehr – Auf György Ligetis Hamburger Pfaden , изд. Манфред Станке , фон Бокель Верлаг, Гамбург, 2005 г., ISBN 3-932696-62-X

[9] Статья в Tonalsoft Encyclopaedia о нотации «HEWM»

[Fonville-10] Джон Фонвилл . «Расширенная четкая интонация Бена Джонстона – руководство для интерпретаторов», стр. 109, «Перспективы новой музыки » , т. 29, № 2 (лето 1991 г.), стр. 106–137. и Джонстон, Бен и Гилмор, Боб (2006). «Система нотации для расширенной четкой интонации» (2003), «Максимальная ясность» и другие сочинения о музыке , стр. 78. ISBN 978-0-252-03098-7

[11] Раш, Рудольф (2002). «Настройка и темперация». В Кристенсене, Т. (ред.). Кембриджская история западной музыкальной теории . Cambridge University Press. стр. 201. ISBN 0-521-62371-5.

[12] Смит, GW "Comma sequences". Xenharmony . Получено 26 июля 2012 г. – через lumma.org.

[13] Монзо, Джо. «Запятая Меркатора / Запятая Меркатора». tonalsoft.com .