Шкала Болена–Пирса


Звукоряд Болена–Пирса ( звукоряд BP ) — это музыкальная настройка и звукоряд , впервые описанные в 1970-х годах, которые предлагают альтернативу октавно -повторяющимся звукам, типичным для западной и других видов музыки [1] , в частности, равномерно темперированному диатоническому звукоряду .
Интервал 3:1 (часто называемый новым названием, тритава ) служит в качестве основного гармонического соотношения, заменяя диатоническую шкалу 2:1 (октаву) на чистую двенадцатую (на октаву выше чистой квинты). Для любой высоты тона, которая является частью шкалы BP, все высоты на одну или более тритав выше или ниже также являются частью системы и считаются эквивалентными.
Шкала BP делит тритаву на 13 ступеней, либо равномерно темперированных (самая популярная форма), либо в справедливо настроенной версии. По сравнению с октавно-повторяющимися шкалами интервалы шкалы BP более созвучны определенным типам акустических спектров . [ необходима цитата ]
Гамму независимо друг от друга описали Хайнц Болен , [2] Кис ван Пруйен [3] и Джон Р. Пирс . Пирс, который вместе с Максом Мэтьюзом и другими опубликовал свое открытие в 1984 году, [4] переименовал гамму Пирса 3579b и ее хроматический вариант в гамму Болена–Пирса, узнав о более ранней публикации Болена. Болен предложил ту же гамму, основываясь на рассмотрении влияния комбинационных тонов на гештальт- впечатление интервалов и аккордов. [5]
Интервалы между классами высоты тона шкалы BP основаны на нечетных целых частотных отношениях, в отличие от интервалов в диатонических гаммах, которые используют как нечетные, так и четные отношения, найденные в гармоническом ряду . В частности, шаги шкалы BP основаны на отношениях целых чисел, множители которых равны 3, 5 и 7. Таким образом, гамма содержит согласные гармонии, основанные на нечетных гармонических обертонах 3:5:7:9 ( ⓘ ). Аккорд, образованный отношением 3:5:7 ( ⓘ ), играет во многом ту же роль, что и аккорд 4:5:6 (мажорное трезвучие ⓘ ) в диатонических гаммах (3:5:7 = 1: 1+2/3 : 2+1/3 и 4:5:6 = 2: 2+1/2 :3 = 1: 1+1/4 : 1+1/2 ).
Аккорды и модуляция
Модель интонационной чувствительности 3:5:7 с похожа на 4:5:6 с (только мажорный аккорд), более похожа, чем у минорного аккорда. [6] Это сходство предполагает, что наши уши также будут воспринимать 3:5:7 как согласный.
Таким образом, аккорд 3:5:7 можно считать мажорным трезвучием гаммы BP. Он аппроксимируется интервалом из 6 равнотемперированных полутонов BP ( ⓘ ) снизу и интервалом из 4 равнотемперированных полутонов сверху (полутоны 0, 6, 10; ⓘ ). Минорное трезвучие — это соответственно 6 полутонов сверху и 4 полутона снизу (0, 4, 10; ⓘ ). 5:7:9 — это первое обращение мажорного трезвучия (0, 4, 7; ⓘ ). [7]
Исследование хроматических трезвучий, образованных из произвольных комбинаций 13 тонов хроматической гаммы среди двенадцати музыкантов и двенадцати неподготовленных слушателей, показало, что полутона 0, 1, 2 являются наиболее диссонирующим аккордом ( ⓘ ), но 0, 11, 13 ( ⓘ ) были сочтены обученными испытуемыми наиболее консонансными (потому что они звучат как мажорное трезвучие с понижением на октаву), а 0, 7, 10 ( ⓘ ) были оценены неподготовленными испытуемыми как наиболее консонансные. [8]
Каждый тон гаммы Pierce 3579b находится в мажорном и минорном трезвучии, за исключением тона II гаммы. Существует тринадцать возможных тональностей. Модуляция возможна путем изменения одной ноты. Перемещение ноты II на один полутон вверх заставляет тонику подняться до того, что было нотой III (полутон 3), которая, следовательно, может считаться доминантой . Можно считать VIII (полутон 10) аналогом субдоминанты . [ 7]
Тембр и тритав

3:1 служит основным гармоническим соотношением, заменяя диатоническую шкалу 2:1 ( октаву ). ( ⓘ ) Этот интервал является чистой двенадцатой в диатонической номенклатуре ( чистая квинта , уменьшенная на октаву), но поскольку эта терминология основана на размерах шагов и функциях, не используемых в шкале BP, его часто называют новым именем, тритава ( ⓘ ), в контексте BP, ссылаясь на его роль как псевдооктавы и используя префикс «три-» (три), чтобы отличить его от октавы. В обычных гаммах, если заданная высота тона является частью системы, то все высоты тона на одну или несколько октав выше или ниже также являются частью системы и, кроме того, считаются эквивалентными . В шкале BP, если присутствует заданная высота тона, то ни одна из высот на одну или несколько октав выше или ниже не присутствует, но все высоты на одну или несколько тритав выше или ниже являются частью системы и считаются эквивалентными.
Использование нечетных целых соотношений в шкале BP подходит для тембров, содержащих только нечетные гармоники. Поскольку спектр кларнета (в регистре шалюмо ) состоит в основном из нечетных гармоник, и инструмент передувается на двенадцатой (или тритаве), а не на октаве, как большинство других духовых инструментов, между ней и шкалой Болена–Пирса существует естественное родство. По предложению композитора Георга Хайду производитель кларнетов Стивен Фокс разработал первые сопрано-кларнеты Болена–Пирса и начал предлагать их для продажи в начале 2006 года. В 2010 году он выпустил первый тенор-кларнет BP (на шесть ступеней ниже сопрано), а в 2011 году — первый эпсилон-кларнет (на четыре ступени выше сопрано). На контракларнете (на одну тритаву ниже сопрано) сейчас (2020) играет Нора Мюллер из Любека, Германия.
Просто настройка
Диатоническую шкалу Болена–Пирса можно построить с помощью следующих точных соотношений (на диаграмме показана шкала «Лямбда» (λ)):
| Примечание | Имя | С | Д | Э | Ф | Г | ЧАС | Дж. | А | Б | С | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Степень | 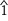 | 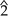 | 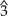 |  | 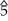 |  | 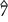 | 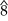 |  | 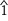 | |||||||||||
| Соотношение | 1:1 | 25:21 | 9:7 | 7:5 | 5:3 | 9:5 | 15:7 | 7:3 | 25:9 | 3:1 | |||||||||||
| Центы | 0 | 301.85 | 435.08 | 582.51 | 884.36 | 1017.60 | 1319.44 | 1466.87 | 1768.72 | 1901.96 | |||||||||||
| Миди | ⓘ | ⓘ | ⓘ | ⓘ | ⓘ | ⓘ | ⓘ | ⓘ | ⓘ | ⓘ | |||||||||||
| Шаг | Имя | Т | с | С | Т | с | Т | С | Т | с | |||||||||||
| Соотношение | 25:21 | 27:25 | 49:45 | 25:21 | 27:25 | 25:21 | 49:45 | 25:21 | 27:25 | ||||||||||||
| Центы | 301.85 | 133.24 | 147.43 | 301.85 | 133.24 | 301.85 | 147.43 | 301.85 | 133.24 | ||||||||||||
Чистая гамма BP может быть построена из четырех перекрывающихся аккордов 3:5:7, например, V, II, VI и IV, хотя для создания похожей гаммы могут быть выбраны и другие аккорды: [9]
(5:3)(7:5)V IX III | III VII I | VI I IV | IV VIII II
Темперамент Болена–Пирса

Болен первоначально выразил шкалу BP как в простой интонации , так и в равномерной темперации . Темперированная форма, которая делит тритаву на тринадцать равных ступеней, стала самой популярной формой. Каждая ступень на 13 √ 3 = 3 1 ⁄ 13 = 1,08818… выше следующей, или на 1200 log 2 (3 1 ⁄ 13 ) = 146,3… центов на ступень. Октава разделена на дробное число ступеней. Двенадцать одинаково темперированных ступеней на октаву используются в 12-тете . Шкалу Болена–Пирса можно описать как 8,202087-тет, потому что полная октава (1200 центов), разделенная на 146,3… центов на ступень, дает 8,202087 ступеней на октаву.
Разделение тритавы на 13 равных шагов темперирует или сводит к унисону оба интервала 245:243 (около 14 центов, иногда называемых минорным диезисом Болена–Пирса ) и 3125:3087 (около 21 цента, иногда называемых мажорным диезисом Болена–Пирса) таким же образом, как разделение октавы на 12 равных шагов сводит к унисону и 81:80 ( синтоническая комма ), и 128:125 ( лимма с 5 пределами ). Линейная темперация с 7 пределами темперирует оба этих интервала; получившаяся темперация Болена–Пирса больше не имеет ничего общего с эквивалентностями тритавы или неоктавными гаммами, за исключением того факта, что она хорошо приспособлена для их использования. Настройка в 41 равный шаг в октаве ( 1200 ⁄ 41 = 29,27 центов на шаг) была бы вполне логичной для этой темперации. В такой настройке темперированная чистая двенадцатая (1902,4 цента, примерно на полцента больше, чем просто двенадцатая) делится на 65 равных шагов, что приводит к кажущемуся парадоксу: взятие каждой пятой ступени этой октавной шкалы дает превосходное приближение к неоктавной равномерно темперированной шкале BP. Более того, интервал из пяти таких шагов генерирует (основанные на октаве) МОС (моменты симметрии) с 8, 9 или 17 нотами, а 8-нотная гамма (включающая ступени 0, 5, 10, 15, 20, 25, 30 и 35 41-нотной шкалы) может считаться эквивалентной октавой версией шкалы Болена–Пирса.
Диаграммы интервалов и масштабов
Ниже приведены тринадцать нот гаммы (центы округлены до ближайшего целого числа):
Справедливо настроенный
| Интервал (центы) | 133 | 169 | 133 | 148 | 154 | 147 | 134 | 147 | 154 | 148 | 133 | 169 | 133 | |||||||||||||||
| Название заметки | С | Д ♭ | Д | Э | Ф | Г ♭ | Г | ЧАС | Дж ♭ | Дж. | А | Б ♭ | Б | С | ||||||||||||||
| Номинал (центы) | 0 | 133 | 302 | 435 | 583 | 737 | 884 | 1018 | 1165 | 1319 | 1467 | 1600 | 1769 | 1902 | ||||||||||||||
Уравновешенный
| Интервал (центы) | 146 | 146 | 146 | 146 | 146 | 146 | 146 | 146 | 146 | 146 | 146 | 146 | 146 | |||||||||||||||
| Название заметки | С | С ♯ /Д ♭ | Д | Э | Ф | Ф ♯ /Г ♭ | Г | ЧАС | Н ♯ /Дж ♭ | Дж. | А | А ♯ /Б ♭ | Б | С | ||||||||||||||
| Номинал (центы) | 0 | 146 | 293 | 439 | 585 | 732 | 878 | 1024 | 1170 | 1317 | 1463 | 1609 | 1756 | 1902 | ||||||||||||||
| Шаги | Имя | интервал эквалайзера | Центы в эквалайзере | Только интонационный интервал | Традиционное название | Центы только в интонации | Разница |
|---|---|---|---|---|---|---|---|
| 0 | С | 3 0 ⁄ 13 = 1,00 | 0.00 | 1:1 = 1,00 | Унисон | 0.00 | 0.00 |
| 1 | До♯/Ре♭ | 3 1 ⁄ 13 = 1,09 | 146.30 | 27:25 = 1,08 | Великая Лимма | 133,24 | 13.06 |
| 2 | Д | 3 2 ⁄ 13 = 1,18 | 292,61 | 25:21 = 1,19 | Квази-темперированная малая терция | 301,85 | −9,24 |
| 3 | Э | 3 3 ⁄ 13 = 1,29 | 438,91 | 9:7 = 1,29 | Септимальная большая терция | 435,08 | 3,83 |
| 4 | Ф | 3 4 ⁄ 13 = 1,40 | 585,22 | 7:5 = 1,40 | Малый септимальный тритон | 582,51 | 2,71 |
| 5 | Фа♯/Соль♭ | 3 5 ⁄ 13 = 1,53 | 731,52 | 75:49 = 1,53 | БП пятый | 736,93 | −5,41 |
| 6 | Г | 3 6 ⁄ 13 = 1,66 | 877,83 | 5:3 = 1,67 | Только большая секста | 884,36 | −6,53 |
| 7 | ЧАС | 3 7 ⁄ 13 = 1,81 | 1024.13 | 9:5 = 1,80 | Больше только малая септаккорда | 1017.60 | 6,53 |
| 8 | H♯/J♭ | 3 8 ⁄ 13 = 1,97 | 1170.44 | 49:25 = 1,96 | ВР восьмой | 1165.02 | 5,42 |
| 9 | Дж. | 3 9 ⁄ 13 = 2,14 | 1316.74 | 15:7 = 2,14 | Септимальная минорная нона | 1319.44 | −2,70 |
| 10 | А | 3 10 ⁄ 13 = 2,33 | 1463.05 | 7:3 = 2,33 | Септимальная минимальная десятая | 1466.87 | −3,82 |
| 11 | А♯/Б♭ | 3 11 ⁄ 13 = 2,53 | 1609.35 | 63:25 = 2,52 | Квази-темперированная большая декада | 1600.11 | 9,24 |
| 12 | Б | 3 12 ⁄ 13 = 2,76 | 1755.66 | 25:9 = 2,78 | Классический увеличенный одиннадцатый | 1768.72 | −13.06 |
| 13 | С | 3 13 ⁄ 13 = 3,00 | 1901.96 | 3:1 = 3,00 | Только двенадцатый, "тритаве" | 1901.96 | 0.00 |
Музыка и композиция

Как звучит музыка, использующая шкалу Болена–Пирса, с эстетической точки зрения ? Дэйв Бенсон предполагает, что полезно использовать только звуки с нечетными гармониками, включая кларнеты или синтезированные тоны, но утверждает, что поскольку «некоторые интервалы звучат немного как интервалы в [более привычной] двенадцатитоновой шкале , но сильно расстроены », среднестатистический слушатель будет постоянно чувствовать, «что что-то не так», из-за социальной обусловленности . [10]
Мэтьюз и Пирс пришли к выводу, что ясные и запоминающиеся мелодии могут быть составлены в шкале BP, что «контрапункт звучит хорошо», и что «аккордовые пассажи звучат как гармония», предположительно, имея в виду прогрессию , «но без какого-либо большого напряжения или чувства разрешения». [11] В их исследовании суждений о консонансе 1989 года оба интервала из пяти аккордов, оцененных обученными музыкантами как наиболее консонантные, приблизительно являются диатоническими интервалами, что предполагает, что их обучение повлияло на их выбор и что аналогичный опыт работы со шкалой BP также повлияет на их выбор. [8]
Композиции, использующие шкалу Болена–Пирса, включают «Purity», первую часть Clang-Tint Кертиса Роудса . [12] Другие компьютерные композиторы, использующие шкалу BP, включают Джона Эпплтона , Ричарда Буланже ( Solemn Song for Evening (1990)), Георга Хайду , ppP Хуана Рейеса (1999-2000), [13] «A Wild and Reckless Place» Эми Радунской (1990), [14] Чарльза Карпентера ( Frog à la Pêche (1994) и Splat ), [15] [16] и Элейн Уокер ( Stick Men (1991), Love Song и Greater Good (2011)). [17]
Дэвид Либерман, доцент кафедры архитектуры в Университете Торонто , руководил разработкой «Stredici», струнного инструмента, настроенного на строй Болена–Пирса. Пятиметровый инструмент использовался на концертах в Бостоне в 2012 году. [18]
Симпозиум
Первый симпозиум Болена–Пирса состоялся в Бостоне 7–9 марта 2010 года, организованный композитором Георгом Хайду ( Hochschule für Musik und Theater Hamburg ) и Boston Microtonal Society . Соорганизаторами выступили Boston Goethe Institute , Berklee College of Music , Northeastern University и New England Conservatory of Music. Участники симпозиума, среди которых были Хайнц Болен, Макс Мэтьюз, Кларенс Барлоу , Кёртис Роудс , Дэвид Вессель, Психея Луи, Ричард Буланже, Георг Хайду, Пол Эрлих , Рон Сворд, Джулия Вернц, Ларри Полански , Манфред Штанке, Стивен Фокс, Элейн Уокер, Тодд Харроп, Гейл Янг, Йоханнес Кретц, Артуро Гролимунд, Кевин Фостер, представили 20 докладов по истории и свойствам шкалы Болена–Пирса, исполнили более 40 композиций в новой системе и представили несколько новых музыкальных инструментов. Среди исполнителей были немецкие музыканты Нора-Луиза Мюллер и Акош Хоффман на кларнетах Болена–Пирса и Артуро Гролимунд на пан-флейте Болена–Пирса, а также канадский ансамбль tranSpectra и американская ксенгармоническая группа ZIA под руководством Элейн Уокер.
Другие необычные настройки или гаммы
Другие неоктавные настройки, исследованные Боленом [19] , включают двенадцать шагов в тритаве, названной Энрике Морено [20] A12 и основанной на аккорде 4:7:10 ⓘ , семь шагов в октаве ( 7-тет ) или аналогичные 11 шагов в тритаве и восемь шагов в октаве, основанной на 5:7:9 ⓘ и из которых будет использоваться только правильная версия. Кроме того, пентаву можно разделить на восемь шагов, что приближает аккорды формы 5:9:13:17:21:25. [21] Шкала Болена в 833 цента основана на последовательности Фибоначчи , хотя она была создана из комбинационных тонов , и содержит сложную сеть гармонических отношений из-за включения совпадающих гармоник сложенных интервалов в 833 цента. Например, «шаг 10 оказывается идентичным октаве (1200 центов) к базовому тону, в то же время демонстрируя Золотое сечение к шагу 3» [22] .
Альтернативные гаммы могут быть определены путем указания размера равномерно темперированных ступеней, например, альфа-гамма Венди Карлос в 78 центов и бета-гамма в 63,8 центов , а также 88-центовая гамма Гэри Моррисона (13,64 шага на октаву или 14 на 1232-центовую растянутую октаву). [23] Это дает альфа-гамму в 15,39 шага на октаву и бета-гамму в 18,75 шага на октаву. [24]
Расширения
39-тоновое равное деление тритавы
Пауль Эрлих предложил разделить каждый шаг Болена-Пирса на терции, так что тритава делится на 39 равных шагов вместо 13 равных шагов. Гамма, которую можно рассматривать как три равномерно разнесенных шкалы Болена-Пирса, дает дополнительные нечетные гармоники. 13-ступенчатая гамма попадает в нечетные гармоники 3:1; 5:3, 7:3; 7:5, 9:5; 9:7 и 15:7; в то время как 39-ступенчатая гамма включает в себя все эти и многие другие (11:5, 13:5; 11:7, 13:7; 11:9, 13:9; 13:11, 15:11, 21:11, 25:11, 27:11; 15:13, 21:13, 25:13, 27:13, 33:13 и 35:13), при этом в ней по-прежнему отсутствуют почти все четные гармоники (включая 2:1; 3:2, 5:2; 4:3, 8:3; 6:5, 8:5; 9:8, 11:8, 13:8 и 15:8). Размер этой шкалы составляет около 25 равных ступеней в соотношении, немного большем, чем октава, поэтому каждая из 39 равных ступеней немного меньше половины одной из 12 равных ступеней стандартной шкалы. [25]
| Количество равномерно темперированных ступеней | Равномерно темперированный интервал | Размер равномерно темперированного интервала (центы) | Справедливо-интонированный интервал | Размер справедливо интонированного интервала (центы) | Ошибка (центов) |
|---|---|---|---|---|---|
| 91 | 12.9802 | 4437.90 | 13/1 | 4440.53 | -2.63 |
| 85 | 10.9617 | 4145.29 | 11/1 | 4151.32 | -6.03 |
| 69 | 6.9845 | 3365.00 | 7/1 | 3368.83 | -3.83 |
| 57 | 4.9812 | 2779.78 | 5/1 | 2786.31 | -6.53 |
| 49 | 3.9761 | 2389.64 | 4/1 | 2400.00 | -10.36 |
| 39 | 3.0000 | 1901.96 | 3/1 | 1901.96 | 0.00 |
| 38 | 2.9167 | 1853.19 | 225/77 | 1856.39 | -3.21 |
| 35/12 | 1853.18 | 0.00 | |||
| 32/11 | 1848.68 | 4.50 | |||
| 189/65 | 1847.85 | 5.34 | |||
| 37 | 2.8357 | 1804.42 | 99/35 | 1800.09 | 4.33 |
| 36 | 2.7569 | 1755.65 | 36/13 | 1763.38 | -7.73 |
| 135/49 | 1754.53 | 1.12 | |||
| 11/7 | 1751.32 | 4.33 | |||
| 35 | 2.6803 | 1706.88 | 35/13 | 1714.61 | -7.73 |
| 34 | 2.6059 | 1658.11 | 13/5 | 1654.21 | 3.90 |
| 33 | 2.5335 | 1609.35 | 63/25 | 1600.11 | 9.24 |
| 33/13 | 1612.75 | -3.40 | |||
| 32 | 2.4631 | 1560.58 | 27/11 | 1554.55 | 6.03 |
| 31 | 2.3947 | 1511.81 | 12/5 | 1515.64 | -3.83 |
| 117/49 | 1506.79 | 5.02 | |||
| 30 | 2.3282 | 1463.04 | 7/3 | 1466.87 | -3.83 |
| 29 | 2.2635 | 1414.27 | 25/11 | 1421.31 | -7.04 |
| 147/65 | 1412.77 | 1.51 | |||
| 28 | 2.2006 | 1365.51 | 11/5 | 1365.00 | 0,50 |
| 27 | 2.1395 | 1316.74 | 15/7 | 1319.44 | -2.70 |
| 26 | 2.0801 | 1267.97 | 27/13 | 1265.34 | 2.63 |
| 25 | 2.0223 | 1219.20 | 99/49 | 1217.58 | 1.63 |
| 24 | 1.9661 | 1170.43 | 49/25 | 1165.02 | 5.41 |
| 23 | 1.9115 | 1121.67 | 21/11 | 1119.46 | 2.20 |
| 22 | 1.8584 | 1072.90 | 13/7 | 1071.70 | 1.20 |
| 21 | 1.8068 | 1024.13 | 9/5 | 1017.60 | 6.53 |
| 20 | 1.7566 | 975.36 | 135/77 | 972.03 | 3.33 |
| 7/4 | 968.83 | 6.54 | |||
| 19 | 1.7078 | 926.59 | 12/7 | 933.13 | -6.54 |
| 77/45 | 929.92 | -3.33 | |||
| 18 | 1.6604 | 877.83 | 5/3 | 884.36 | -6.53 |
| 17 | 1.6143 | 829.06 | 21/13 | 830.25 | -1.20 |
| 16 | 1.5694 | 780.29 | 11/7 | 782.49 | -2.20 |
| 15 | 1.5258 | 731.52 | 75/49 | 736.93 | -5.41 |
| 14 | 1.4835 | 682.75 | 49/33 | 684.38 | -1.63 |
| 13 | 1.4422 | 633,99 | 13/9 | 636.62 | -2.63 |
| 12 | 1.4022 | 585.22 | 7/5 | 582.51 | 2.70 |
| 11 | 1.3632 | 536.45 | 15/11 | 536.95 | -0,50 |
| 10 | 1.3254 | 487.68 | 65/49 | 489.19 | -1.51 |
| 33/25 | 480,65 | 7.04 | |||
| 9 | 1.2886 | 438.91 | 9/7 | 435.08 | 3.83 |
| 8 | 1.2528 | 390.14 | 49/39 | 395.17 | -5.02 |
| 5/4 | 386.31 | 3.83 | |||
| 7 | 1.2180 | 341.38 | 11/9 | 347.41 | -6.03 |
| 6 | 1.1841 | 292.61 | 13/11 | 289.21 | 3.40 |
| 25/21 | 301.85 | -9.24 | |||
| 5 | 1.1512 | 243,84 | 15/13 | 247.74 | -3.90 |
| 4 | 1.1193 | 195.07 | 39/35 | 187.34 | 7.73 |
| 3 | 1.0882 | 146.30 | 12/11 | 150,64 | -4.33 |
| 49/45 | 147.43 | -1.12 | |||
| 13/12 | 138,57 | 7.73 | |||
| 2 | 1.0580 | 97.54 | 35/33 | 101.87 | -4.33 |
| 1 | 1.0286 | 48.77 | 65/63 | 54.11 | -5.34 |
| 33/32 | 53.27 | -4.50 | |||
| 36/35 | 48.77 | 0.00 | |||
| 77/75 | 45.56 | 3.21 | |||
| 0 | 1.0000 | 0.00 | 1/1 | 0.00 | 0.00 |
65-тоновое равное деление тритавы
Разделение каждой ступени шкалы Болена–Пирса на квинты (так что тритава делится на 65 ступеней) приводит к очень точной октаве (41 ступень) и чистой квинте (24 ступени), а также к приближениям для других точных интервалов. Шкала практически идентична 41-тоновому равному делению октавы, за исключением того, что каждая ступень немного меньше (менее сотой доли цента на ступень).
| Количество равномерно темперированных ступеней | Равномерно темперированный интервал | Размер равномерно темперированного интервала (центы) | Справедливо-интонированный интервал | Размер справедливо интонированного интервала (центы) | Ошибка (центов) |
|---|---|---|---|---|---|
| 65 | 3.0000 | 1901.96 | 3/1 | 1901.9550 | 0.00 |
| 64 | 2.9497 | 1872.69 | 144/49 | 1866.2582 | 6.44 |
| 63 | 2.9003 | 1843.43 | 32/11 | 1848.6821 | -5.25 |
| 62 | 2.8517 | 1814.17 | 20/7 | 1817.4878 | -3.32 |
| 61 | 2.8039 | 1784.91 | 14/5 | 1782.5122 | 2.40 |
| 60 | 2.7569 | 1755.65 | 135/49 | 1754.5269 | 1.12 |
| 11/4 | 1751.3179 | 4.33 | |||
| 59 | 2.7107 | 1726.39 | 27/10 | 1719.5513 | 6.84 |
| 58 | 2.6653 | 1697.13 | 8/3 | 1698.0450 | -0,92 |
| 57 | 2.6206 | 1667.87 | 21/8 | 1670.7809 | -2.91 |
| 56 | 2.5767 | 1638.61 | 18/7 | 1635.0841 | 3.52 |
| 55 | 2.5335 | 1609.35 | 81/32 | 1607.8200 | 1.53 |
| 54 | 2.4910 | 1580.09 | 5/2 | 1586.3137 | -6.23 |
| 53 | 2.4493 | 1550.82 | 27/11 | 1554.5471 | -3.72 |
| 52 | 2.4082 | 1521.56 | 12/5 | 1515.6413 | 5.92 |
| 51 | 2.3679 | 1492.30 | 64/27 | 1494.1350 | -1.83 |
| 50 | 2.3282 | 1463.04 | 7/3 | 1466.8709 | -3.83 |
| 49 | 2.2892 | 1433,78 | 16/7 | 1431.1741 | 2.61 |
| 48 | 2.2508 | 1404.52 | 9/4 | 1403.9100 | 0,61 |
| 47 | 2.2131 | 1375.26 | 20/9 | 1382.4037 | -7.14 |
| 46 | 2.1760 | 1346.00 | 24/11 | 1350.6371 | -4,64 |
| 45 | 2.1395 | 1316.74 | 15/7 | 1319.4428 | -2.70 |
| 44 | 2.1037 | 1287.48 | 21/10 | 1284.4672 | 3.01 |
| 43 | 2.0684 | 1258.22 | 33/16 | 1253.2729 | 4.94 |
| 42 | 2.0337 | 1228.96 | 55/27 | 1231.7667 | -2.81 |
| 41 | 1.9996 | 1199.69 | 2/1 | 1200.0000 | -0,31 |
| 40 | 1.9661 | 1170.43 | 49/25 | 1165.0244 | 5.41 |
| 39 | 1.9332 | 1141.17 | 27/14 | 1137.0391 | 4.13 |
| 38 | 1.9008 | 1111.91 | 40/21 | 1115.5328 | -3.62 |
| 37 | 1.8689 | 1082.65 | 15/8 | 1088.2687 | -5.62 |
| 36 | 1.8376 | 1053.39 | 11/6 | 1049.3629 | 4.03 |
| 35 | 1.8068 | 1024.13 | 9/5 | 1017.5963 | 6.53 |
| 34 | 1.7765 | 994.87 | 16/9 | 996.0900 | -1.22 |
| 33 | 1.7468 | 965.61 | 7/4 | 968.8259 | -3.22 |
| 32 | 1.7175 | 936.35 | 12/7 | 933.1291 | 3.22 |
| 31 | 1.6887 | 907.09 | 27/16 | 905.8650 | 1.22 |
| 30 | 1.6604 | 877.83 | 5/3 | 884.3587 | -6.53 |
| 29 | 1.6326 | 848.56 | 18/11 | 852.5921 | -4.03 |
| 28 | 1.6052 | 819.30 | 8/5 | 813.6863 | 5.62 |
| 27 | 1.5783 | 790.04 | 63/40 | 786.4222 | 3.62 |
| 26 | 1.5518 | 760,78 | 14/9 | 764.9159 | -4.13 |
| 25 | 1.5258 | 731.52 | 32/21 | 729.2191 | 2.30 |
| 24 | 1.5003 | 702.26 | 3/2 | 701.9550 | 0,31 |
| 23 | 1.4751 | 673.00 | 81/55 | 670.1883 | 2.81 |
| 72/49 | 666.2582 | 6.74 | |||
| 22 | 1.4504 | 643.74 | 16/11 | 648.6821 | -4,94 |
| 21 | 1.4261 | 614.48 | 10/7 | 617.4878 | -3.01 |
| 20 | 1.4022 | 585.22 | 7/5 | 582.5122 | 2.70 |
| 19 | 1.3787 | 555,96 | 11/8 | 551.3179 | 4.64 |
| 18 | 1.3556 | 526.70 | 27/20 | 519.5513 | 7.14 |
| 17 | 1.3329 | 497.43 | 4/3 | 498.0450 | -0,61 |
| 16 | 1.3105 | 468.17 | 21/16 | 470.7809 | -2.61 |
| 15 | 1.2886 | 438.91 | 9/7 | 435.0841 | 3.83 |
| 14 | 1.2670 | 409.65 | 80/63 | 413.5778 | -3.93 |
| 81/64 | 407.8200 | 1.83 | |||
| 13 | 1.2457 | 380.39 | 5/4 | 386.3137 | -5.92 |
| 12 | 1.2249 | 351.13 | 11/9 | 347.4079 | 3.72 |
| 11 | 1.2043 | 321,87 | 6/5 | 315.6413 | 6.23 |
| 10 | 1.1841 | 292.61 | 32/27 | 294.1350 | -1.53 |
| 9 | 1.1643 | 263,35 | 7/6 | 266.8709 | -3.52 |
| 8 | 1.1448 | 234.09 | 8/7 | 231.1741 | 2.91 |
| 7 | 1.1256 | 204.83 | 9/8 | 203.9100 | 0,92 |
| 6 | 1.1067 | 175,57 | 10/9 | 182.4037 | -6.84 |
| 5 | 1.0882 | 146.30 | 12/11 | 150.6371 | -4.33 |
| 49/45 | 147.4281 | -1.12 | |||
| 4 | 1.0699 | 117.04 | 15/14 | 119.4428 | -2.40 |
| 16/15 | 111.7313 | 5.31 | |||
| 3 | 1.0520 | 87.78 | 21/20 | 84.4672 | 3.32 |
| 2 | 1.0344 | 58.52 | 28/27 | 62.9609 | -4.44 |
| 33/32 | 53.2729 | 5.25 | |||
| 1 | 1.0170 | 29.26 | 49/48 | 35.6968 | -6.44 |
| 50/49 | 34.9756 | -5.71 | |||
| 55/54 | 31.7667 | -2.51 | |||
| 56/55 | 31.1943 | -1,93 | |||
| 64/63 | 27.2641 | 2.00 | |||
| 0 | 1.0000 | 0.00 | 1/1 | 0.0000 | 0.00 |
Смотрите также
- Двойная трость
- Прямоугольная волна
- Другие неоктавные повторяющиеся гаммы:
Ссылки
- ^ ab Pierce, John R. (2001). "Консонанс и гаммы". В Cook, Perry R (ред.). Музыка, познание и компьютеризированный звук: введение в психоакустику . MIT Press. стр. 183. ISBN 978-0-262-53190-0.
- ^ Болен, Хайнц (1978). «13 Тонстуфенов в Дуодезиме». Акустика (на немецком языке). 39 (2). Штутгарт: С. Хирзель Верлаг : 76–86 . Проверено 27 ноября 2012 г.
- ^ Пройен, Кес ван (1978). «Теория равнотемперированных весов». Интерфейс . 7 : 45–56 . дои : 10.1080/09298217808570248 . Проверено 27 ноября 2012 г.
- ^ Mathews, MV; Roberts, LA; Pierce, JR (1984). "Четыре новых гаммы на основе аккордов с непоследовательным целым отношением". J. Acoust. Soc. Am. 75, S10(A) (S1): S10. Bibcode :1984ASAJ...75...10M. doi : 10.1121/1.2021272 .
- ^ Мэтьюз, Макс В.; Пирс, Джон Р. (1989). "Шкала Болена–Пирса". В Мэтьюз, Макс В.; Пирс, Джон Р. (ред.). Текущие направления в исследованиях компьютерной музыки . MIT Press. стр. 167. ISBN 9780262631396.
- ↑ Мэтьюз и Пирс (1989), стр. 165–166.
- ^ ab Mathews & Pierce (1989), стр. 169
- ^ ab Mathews & Pierce (1989), стр. 171
- ^ Мэтьюз; Пирс (1989). стр. 170.
- ^ Бенсон, Дэйв. «Музыкальные гаммы и чертова дюжина». Музыка и математика . 28/06: 16.
- ^ Мэтьюз; Пирс (1989). стр. 172.
- ↑ Thrall, Michael Voyne (лето 1997 г.). «Synthèse 96: 26-й Международный Фестиваль Электроакустической Музыки». Computer Music Journal . 21 (2): 90–92 [91]. doi :10.2307/3681110. JSTOR 3681110.
- ^ "Джон Пирс (1910-2002)". Computer Music Journal . 26, № 4 (Языки и среды для компьютерной музыки): 6–7 . Зима 2002.
- ^ Дискография микротональных компакт-дисков, Huygens-Fokker Foundation , получено 13 декабря 2016 г..
- ^ d'Escrivan, Julio (2007). Коллинз, Ник (ред.). Cambridge Companion to Electronic Music . Cambridge Companions to Music . стр. 229. ISBN 9780521868617.
- ^ Бенсон, Дэйв (2006). Музыка: Математическое предложение . стр. 237. ISBN 9780521853873.
- ^ "Концерты". Bohlen-Pierce-Conference.org . Получено 27 ноября 2012 г. .
- ^ "Дэвид Либерман принимает участие в выставке Electric Fields and Mini-Maker Faire | Daniels". www.daniels.utoronto.ca . Получено 04.01.2023 .
- ^ Болен (1978). сноска 26, стр. 84.
- ^ "Другие необычные весы". Сайт Болена–Пирса . Получено 27 ноября 2012 г.Цитаты: Moreno, Enrique Ignacio (декабрь 1995 г.). «Вложение пространств равной высоты и вопрос расширенных цветностей: экспериментальный подход». Диссертация . Стэнфордский университет: 12–22 .
- ^ «Другие необычные весы», The Bohlen–Pierce Site . Получено 27 ноября 2012 г. Цитируется: Bohlen (1978). стр. 76–86.
- ^ Болен, Хайнц. «Шкала 833 цента». Сайт Болена-Пирса . Проверено 27 ноября 2012 г.
- ^ Sethares, William (2004). Настройка, тембр, спектр, масштаб . стр. 60. ISBN 1-85233-797-4.
- ^ Карлос, Венди (2000) [1986]. «Примечания». Красавица и чудовище (CD). Венди Карлос. ESD. 81552.
- ^ "BP Scale Structures". Сайт Болена–Пирса . Получено 27 ноября 2012 г.
Внешние ссылки
- Исследование «Шкала Болена–Пирса», ZiaSpace.com .
- «Кларнеты Стивена Фокса», кларнеты и другие инструменты Болена-Пирса, SFoxClarinets.com .
- «Сайт Болена–Пирса: веб-сайт альтернативной гармонической шкалы», Huygens-Fokker.org .
- «Кес ван Пройен: 13 тонов в 3-й гармонике» , Kees.cc.
- Песня в тональности Болена Пирса: «17tppp4 Walker Love Song», Xenharmonic.Wikispaces.com .
- «Симпозиум Болена-Пирса», Bohlen-Pierce-Conference.org .
- «Симпозиум по шкале Болена–Пирса, Бостон 2010» [плейлист], YouTube.com .