Конверт (волны)
Плавная кривая, описывающая крайние значения колеблющегося сигнала

В физике и технике огибающая колеблющегося сигнала представляет собой плавную кривую , описывающую его экстремумы. [1] Таким образом, огибающая обобщает концепцию постоянной амплитуды в мгновенную амплитуду . На рисунке показана модулированная синусоида, изменяющаяся между верхней и нижней огибающей . Функция огибающей может быть функцией времени, пространства, угла или любой другой переменной.

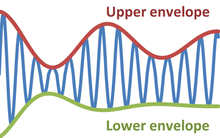
Огибающая модулированной синусоидальной волны.

В бьющихся волнах

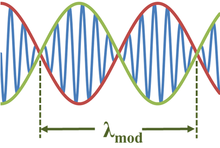
Модулированная волна, полученная в результате сложения двух синусоидальных волн одинаковой амплитуды и почти одинаковой длины волны и частоты.

Распространенной ситуацией, приводящей к появлению огибающей функции как в пространстве x, так и во времени t, является суперпозиция двух волн почти одинаковой длины волны и частоты: [2]

Ф ( х ,   т ) = грех ⁡ [ 2 π ( х λ − Δ λ − ( ф + Δ ф ) т ) ] + грех ⁡ [ 2 π ( х λ + Δ λ − ( ф − Δ ф ) т ) ] ≈ 2 потому что ⁡ [ 2 π ( х λ м о г − Δ ф   т ) ]   грех ⁡ [ 2 π ( х λ − ф   т ) ] {\displaystyle {\begin{aligned}F(x,\ t)&=\sin \left[2\pi \left({\frac {x}{\lambda -\Delta \lambda }}-(f+\Delta f)t\right)\right]+\sin \left[2\pi \left({\frac {x}{\lambda +\Delta \lambda }}-(f-\Delta f)t\right)\right]\\[6pt]&\approx 2\cos \left[2\pi \left({\frac {x}{\lambda _{\rm {mod}}}}-\Delta f\ t\right)\right]\ \sin \left[2\pi \left({\frac {x}{\lambda }}-f\ t\right)\right]\end{выровнено}}}

который использует тригонометрическую формулу для сложения двух синусоид и приближение Δ λ  ≪  λ :

1 λ ± Δ λ = 1 λ   1 1 ± Δ λ / λ ≈ 1 λ ∓ Δ λ λ 2 . {\displaystyle {\frac {1}{\lambda \pm \Delta \lambda }}={\frac {1}{\lambda }}\ {\frac {1}{1\pm \Delta \lambda /\lambda }}\approx {\frac {1}{\lambda }}\mp {\frac {\Delta \lambda }{\lambda ^{2}}}.}

Здесь длина волны модуляции λ mod определяется по формуле: [2] [3]

λ м о г = λ 2 Δ λ   . {\displaystyle \lambda _{\rm {mod}}={\frac {\lambda ^{2}}{\Delta \lambda }}\ .}

Длина волны модуляции вдвое больше самой огибающей, поскольку каждая половина длины волны модулирующей косинусоидальной волны управляет как положительными, так и отрицательными значениями модулированной синусоидальной волны. Аналогично частота биений равна частоте огибающей, вдвое больше модулирующей волны, или 2Δ f . [4]

Если эта волна является звуковой волной, ухо слышит частоту, связанную с f , а амплитуда этого звука меняется в зависимости от частоты биений. [4]

Фазовая и групповая скорость

Красный квадрат движется с фазовой скоростью , а зеленые круги распространяются с групповой скоростью .

Аргумент синусоид выше, за исключением множителя 2π , равен:

ξ С = ( х λ − ф   т )   , {\displaystyle \xi _{C}=\left({\frac {x}{\lambda }}-f\ t\right)\ ,}
ξ E = ( x λ m o d − Δ f   t )   , {\displaystyle \xi _{E}=\left({\frac {x}{\lambda _{\rm {mod}}}}-\Delta f\ t\right)\ ,}

с индексами C и E, относящимися к несущей и огибающей . Одна и та же амплитуда F волны получается из одних и тех же значений ξ C и ξ E , каждое из которых может само по себе вернуться к одному и тому же значению при различных, но правильно связанных вариантах выбора x и t . Эта инвариантность означает, что можно проследить эти формы волн в пространстве, чтобы найти скорость положения фиксированной амплитуды по мере его распространения во времени; для того, чтобы аргумент несущей волны оставался тем же, условие таково:

( x λ − f   t ) = ( x + Δ x λ − f ( t + Δ t ) )   , {\displaystyle \left({\frac {x}{\lambda }}-f\ t\right)=\left({\frac {x+\Delta x}{\lambda }}-f(t+\Delta t)\right)\ ,}

что показывает, что для поддержания постоянной амплитуды расстояние Δ x связано с интервалом времени Δ t так называемой фазовой скоростью v p

v p = Δ x Δ t = λ f   . {\displaystyle v_{\rm {p}}={\frac {\Delta x}{\Delta t}}=\lambda f\ .}

С другой стороны, те же соображения показывают, что огибающая распространяется с так называемой групповой скоростью v g : [5]

v g = Δ x Δ t = λ m o d Δ f = λ 2 Δ f Δ λ   . {\displaystyle v_{\rm {g}}={\frac {\Delta x}{\Delta t}}=\lambda _{\rm {mod}}\Delta f=\lambda ^{2}{\frac {\Delta f}{\Delta \lambda }}\ .}

Более общее выражение для групповой скорости получается путем введения волнового вектора k :

k = 2 π λ   . {\displaystyle k={\frac {2\pi }{\lambda }}\ .}

Заметим, что для малых изменений Δ λ величина соответствующего малого изменения волнового вектора, скажем, Δ k , равна:

Δ k = | d k d λ | Δ λ = 2 π Δ λ λ 2   , {\displaystyle \Delta k=\left|{\frac {dk}{d\lambda }}\right|\Delta \lambda =2\pi {\frac {\Delta \lambda }{\lambda ^{2}}}\ ,}

поэтому групповую скорость можно переписать как:

v g = 2 π Δ f Δ k = Δ ω Δ k   , {\displaystyle v_{\rm {g}}={\frac {2\pi \Delta f}{\Delta k}}={\frac {\Delta \omega }{\Delta k}}\ ,}

где ω — частота в радианах/с: ω = 2 π f . Во всех средах частота и волновой вектор связаны дисперсионным соотношением , ω = ω ( k ), а групповая скорость может быть записана:

v g = d ω ( k ) d k   . {\displaystyle v_{\rm {g}}={\frac {d\omega (k)}{dk}}\ .}
Дисперсионное соотношение ω=ω( k ) для некоторых волн, соответствующих колебаниям решетки в GaAs. [6]

В такой среде, как классический вакуум, дисперсионное соотношение для электромагнитных волн имеет вид:

ω = c 0 k {\displaystyle \omega =c_{0}k}

где c 0 — скорость света в классическом вакууме. Для этого случая фазовая и групповая скорости равны c 0 .

В так называемых дисперсионных средах дисперсионное соотношение может быть сложной функцией волнового вектора, а фазовая и групповая скорости не совпадают. Например, для нескольких типов волн, демонстрируемых атомными колебаниями ( фононами ) в GaAs , дисперсионные соотношения показаны на рисунке для различных направлений волнового вектора k . В общем случае фазовая и групповая скорости могут иметь разные направления. [7]

В приближении функции

Вероятности электронов в двух нижних квантовых состояниях квантовой ямы GaAs размером 160Å в гетероструктуре GaAs- GaAlAs , рассчитанные с помощью огибающих функций. [8]

В физике конденсированного состояния собственная функция энергии для подвижного носителя заряда в кристалле может быть выражена в виде волны Блоха :

ψ n k ( r ) = e i k ⋅ r u n k ( r )   , {\displaystyle \psi _{n\mathbf {k} }(\mathbf {r} )=e^{i\mathbf {k} \cdot \mathbf {r} }u_{n\mathbf {k} }(\mathbf {r} )\ ,}

где n - индекс зоны (например, зоны проводимости или валентной зоны), r - пространственное местоположение, а k - волновой вектор . Экспонента - это синусоидально изменяющаяся функция, соответствующая медленно меняющейся огибающей, модулирующей быстро меняющуюся часть волновой функции u n , k описывает поведение волновой функции вблизи ядер атомов решетки. Огибающая ограничена значениями k в диапазоне, ограниченном зоной Бриллюэна кристалла, и это ограничивает то, насколько быстро она может меняться в зависимости от местоположения r .

При определении поведения носителей с использованием квантовой механики обычно используется приближение огибающей, в котором уравнение Шредингера упрощается , чтобы относиться только к поведению огибающей, а граничные условия применяются непосредственно к огибающей функции, а не к полной волновой функции. [9] Например, волновая функция носителя, захваченного вблизи примеси, управляется огибающей функцией F , которая управляет суперпозицией функций Блоха:

ψ ( r ) = ∑ k F ( k ) e i k ⋅ r u k ( r )   , {\displaystyle \psi (\mathbf {r} )=\sum _{\mathbf {k} }F(\mathbf {k} )e^{i\mathbf {k\cdot r} }u_{\mathbf {k} }(\mathbf {r} )\ ,}

где компоненты Фурье огибающей F ( k ) находятся из приближенного уравнения Шредингера. [10] В некоторых приложениях периодическая часть uk заменяется ее значением вблизи края зоны, скажем k = k 0 , и тогда: [9]

ψ ( r ) ≈ ( ∑ k F ( k ) e i k ⋅ r ) u k = k 0 ( r ) = F ( r ) u k = k 0 ( r )   . {\displaystyle \psi (\mathbf {r} )\approx \left(\sum _{\mathbf {k} }F(\mathbf {k} )e^{i\mathbf {k\cdot r} }\right)u_{\mathbf {k} =\mathbf {k} _{0}}(\mathbf {r} )=F(\mathbf {r} )u_{\mathbf {k} =\mathbf {k} _{0}}(\mathbf {r} )\ .}

В дифракционных картинах

Дифракционная картина двойной щели имеет огибающую одной щели.

Дифракционные картины от нескольких щелей имеют огибающие, определяемые дифракционной картиной от одной щели. Для одной щели картина определяется как: [11]

I 1 = I 0 sin 2 ⁡ ( π d sin ⁡ α λ ) / ( π d sin ⁡ α λ ) 2   , {\displaystyle I_{1}=I_{0}\sin ^{2}\left({\frac {\pi d\sin \alpha }{\lambda }}\right)/\left({\frac {\pi d\sin \alpha }{\lambda }}\right)^{2}\ ,}

где α — угол дифракции, d — ширина щели, а λ — длина волны. Для нескольких щелей картина [11]

I q = I 1 sin 2 ⁡ ( q π g sin ⁡ α λ ) / sin 2 ⁡ ( π g sin ⁡ α λ )   , {\displaystyle I_{q}=I_{1}\sin ^{2}\left({\frac {q\pi g\sin \alpha }{\lambda }}\right)/\sin ^{2}\left({\frac {\pi g\sin \alpha }{\lambda }}\right)\ ,}

где q — число щелей, а g — постоянная решетки. Первый фактор, результат одной щели I 1 , модулирует более быстро меняющийся второй фактор, который зависит от числа щелей и их расстояния.

Оценка

Детектор огибающей — это схема , которая пытается извлечь огибающую из аналогового сигнала .

При цифровой обработке сигналов огибающую можно оценить с помощью преобразования Гильберта или движущейся среднеквадратичной амплитуды . [12]

Смотрите также

Ссылки

  1. ^ C. Richard Johnson, Jr; William A. Sethares; Andrew G. Klein (2011). "Рисунок C.1: Огибающая функции плавно очерчивает свои экстремумы". Software Receiver Design: Build Your Own Digital Communication System in Five Easy Steps . Cambridge University Press. стр. 417. ISBN 978-0521189446.
  2. ^ ab Blair Kinsman (2002). Ветровые волны: их генерация и распространение на поверхности океана (переиздание Prentice-Hall 1965 ed.). Courier Dover Publications . стр. 186. ISBN 0486495116.
  3. ^ Марк В. Денни (1993). Воздух и вода: биология и физика среды жизни . Princeton University Press . стр. 289. ISBN 0691025185.
  4. ^ ab Пол Аллен Типлер; Джин Моска (2008). Физика для ученых и инженеров, том 1 (6-е изд.). Macmillan. стр. 538. ISBN 978-1429201247.
  5. ^ Питер В. Милонни ; Джозеф Х. Эберли (2010). "§8.3 Групповая скорость". Laser Physics (2-е изд.). John Wiley & Sons . стр. 336. ISBN 978-0470387719.
  6. ^ Питер Ю. Ю; Мануэль Кардона (2010). "Рис. 3.2: Фононные дисперсионные кривые в GaAs вдоль высокосимметричных осей". Основы полупроводников: физика и свойства материалов (4-е изд.). Springer. стр. 111. ISBN 978-3642007095.
  7. ^ V. Cerveny; Vlastislav Červený (2005). "§2.2.9 Связь между векторами фазовой и групповой скорости". Seismic Ray Theory . Cambridge University Press . стр. 35. ISBN 0521018226.
  8. ^ G Bastard; JA Brum; R Ferreira (1991). "Рисунок 10 в электронных состояниях в полупроводниковых гетероструктурах". В Henry Ehrenreich; David Turnbull (ред.). Физика твердого тела: полупроводниковые гетероструктуры и наноструктуры . Academic Press. стр. 259. ISBN 0126077444.
  9. ^ ab Christian Schüller (2006). "§2.4.1 Аппроксимация огибающей функции (EFA)". Неупругое рассеяние света полупроводниковыми наноструктурами: основы и последние достижения . Springer. стр. 22. ISBN 3540365257.
  10. ^ Например, см. Marco Fanciulli (2009). "§1.1 Приближение огибающей функции". Электронный спиновый резонанс и связанные с ним явления в низкоразмерных структурах . Springer. стр. 224 и далее . ISBN 978-3540793649.
  11. ^ ab Kordt Griepenkerl (2002). "Распределение интенсивности для дифракции на щели и картина интенсивности для дифракции на решетке". В John W Harris; Walter Benenson; Horst Stöcker; Holger Lutz (ред.). Справочник по физике . Springer. стр. 306 и далее . ISBN 0387952691.
  12. ^ "Извлечение огибающей - MATLAB и Simulink". MathWorks . 2021-09-02 . Получено 2021-11-16 .

В данной статье использованы материалы статьи Citizendium «Функция конверта», которая распространяется по лицензии Creative Commons Attribution-ShareAlike 3.0 Unported License , но не по лицензии GFDL .

Retrieved from "https://en.wikipedia.org/w/index.php?title=Envelope_(waves)&oldid=1234740353"