Монотонная функция

В математике монотонная функция ( или монотонная функция ) — это функция между упорядоченными множествами , которая сохраняет или меняет заданный порядок . ^{[1] [2] [3]} Это понятие впервые возникло в исчислении , а затем было обобщено до более абстрактной области теории порядка .

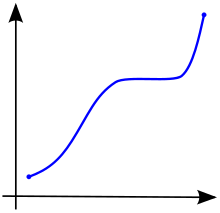
В исчислении функция, определенная на подмножестве действительных чисел с действительными значениями, называется монотонной, если она либо полностью не убывает, либо полностью не возрастает. ^[2] То есть, согласно рис. 1, функция, которая монотонно возрастает, не обязательно должна возрастать, она просто не должна убывать.${\displaystyle f}$

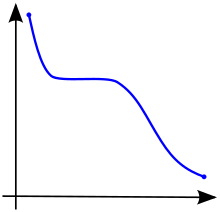
Функция называется монотонно возрастающей (также возрастающей или неубывающей ) ^[3] , если для всех и таких, что , поэтому сохраняет порядок (см. Рисунок 1). Аналогично, функция называется монотонно убывающей (также убывающей или неубывающей ) ^[3], если всякий раз , то , поэтому она меняет порядок на противоположный (см. Рисунок 2).${\displaystyle x}$${\displaystyle у}$${\displaystyle x\leq y}$${\displaystyle f\!\left(x\right)\leq f\!\left(y\right)}$${\displaystyle f}$${\displaystyle x\leq y}$${\displaystyle f\!\left(x\right)\geq f\!\left(y\right)}$

Если порядок в определении монотонности заменить на строгий порядок , то получим более сильное требование. Функция с этим свойством называется строго возрастающей (также возрастающей ). ^{[3] [4]} Опять же, инвертируя символ порядка, можно найти соответствующее понятие, называемое строго убывающей (также убывающей ). ^{[3] [4]} Функция с любым из свойств называется строго монотонной . Строго монотонные функции являются взаимно однозначными (потому что для не равно , либо или и поэтому, по монотонности, либо или , таким образом .)${\displaystyle \leq}$${\стиль_отображения <}$${\displaystyle x}$${\displaystyle у}$${\displaystyle x<y}$${\displaystyle х>у}$${\displaystyle f\!\left(x\right)<f\!\left(y\right)}$${\displaystyle f\!\left(x\right)>f\!\left(y\right)}$${\displaystyle f\!\left(x\right)\neq f\!\left(y\right)}$

Чтобы избежать двусмысленности, для обозначения нестрогой монотонности часто используют термины «слабо монотонный» , «слабо возрастающий» и «слабо убывающий» .

Термины «неубывающий» и «невозрастающий» не следует путать с (гораздо более слабыми) отрицательными определениями «не убывающий» и «не возрастающий». Например, немонотонная функция, показанная на рисунке 3, сначала падает, затем растет, затем снова падает. Следовательно, она не убывает и не возрастает, но она не является ни неубывающей, ни невозрастающей.

Говорят, что функция абсолютно монотонна на интервале, если производные всех порядков неотрицательны или все неположительны во всех точках интервала .${\displaystyle f}$${\displaystyle \left(a,b\right)}$${\displaystyle f}$

Все строго монотонные функции обратимы, поскольку они гарантированно имеют взаимно-однозначное отображение своего диапазона определения в свою область определения.

Однако функции, которые являются лишь слабо монотонными, необратимы, поскольку они постоянны на некотором интервале (и, следовательно, не являются взаимно однозначными).

Функция может быть строго монотонной в ограниченном диапазоне значений и, таким образом, иметь обратную функцию в этом диапазоне, даже если она не является строго монотонной везде. Например, если строго возрастает в диапазоне , то она имеет обратную функцию в диапазоне .${\displaystyle y=g(x)}$${\displaystyle [а,б]}$${\displaystyle x=h(y)}$${\displaystyle [г(а),г(б)]}$

Термин «монотонный» иногда используется вместо «строго монотонный» , поэтому источник может утверждать, что все монотонные функции обратимы, хотя на самом деле подразумевается, что все строго монотонные функции обратимы. ^{[ требуется ссылка ]}

Термин монотонное преобразование (или монотонное преобразование ) также может вызывать путаницу, поскольку он относится к преобразованию строго возрастающей функцией. Это имеет место в экономике в отношении порядковых свойств функции полезности , сохраняющихся при монотонном преобразовании (см. также монотонные предпочтения ). ^[5] В этом контексте термин «монотонное преобразование» относится к положительному монотонному преобразованию и призван отличать его от «отрицательного монотонного преобразования», которое меняет порядок чисел на противоположный. ^[6]

Для монотонной функции справедливы следующие свойства :${\displaystyle f\двоеточие \mathbb {R} \to \mathbb {R} }$

• ${\displaystyle f}$имеет пределы справа и слева в каждой точке своей области определения ;
• ${\displaystyle f}$имеет предел на положительной или отрицательной бесконечности ( ) либо действительного числа, , либо .${\displaystyle \pm \infty }$${\displaystyle \infty}$${\displaystyle -\infty}$
• ${\displaystyle f}$может иметь только скачки разрывов ;
• ${\displaystyle f}$может иметь только счетное число разрывов в своей области определения. Однако разрывы не обязательно состоят из изолированных точек и могут быть даже плотными в интервале ( a , b ). Например, для любой суммируемой последовательности положительных чисел и любого перечисления рациональных чисел монотонно возрастающая функция непрерывна точно для каждого иррационального числа (ср. рисунок). Это кумулятивная функция распределения дискретной меры по рациональным числам, где — вес .$(а_{я})$${\displaystyle (q_{i})}$$${\displaystyle f(x)=\sum _{q_{i}\leq x}a_{i}}$$${\displaystyle a_{i}}$${\displaystyle q_{i}}$
• Если дифференцируема в точках и , то существует невырожденный интервал I такой, что и возрастает на I. Как частичное обратное утверждение, если f дифференцируема и возрастает на интервале I , то ее производная положительна в каждой точке I .${\displaystyle f}$${\displaystyle x^{*}\in {\mathbb {R}}}$${\displaystyle f'(x^{*})>0}$ ${\displaystyle x^{*}\in I}$${\displaystyle f}$

Эти свойства являются причиной того, что монотонные функции полезны в технической работе в анализе . Другие важные свойства этих функций включают:

• если — монотонная функция, определенная на интервале , то дифференцируема почти всюду на ; т. е. множество чисел из , такое что не дифференцируемо в , имеет меру Лебега нулевую . Кроме того, этот результат нельзя улучшить до счетного: см. функцию Кантора .${\displaystyle f}$ ${\displaystyle I}$${\displaystyle f}$ ${\displaystyle I}$${\displaystyle x}$${\displaystyle I}$${\displaystyle f}$${\displaystyle x}$
• если это множество счетно, то оно абсолютно непрерывно${\displaystyle f}$
• если — монотонная функция, определенная на интервале , то она интегрируема по Риману .${\displaystyle f}$${\displaystyle \left[a,b\right]}$${\displaystyle f}$

Важное применение монотонных функций — в теории вероятностей . Если — случайная величина , то ее кумулятивная функция распределения — монотонно возрастающая функция.${\displaystyle X}$ ${\displaystyle F_{X}\!\left(x\right)={\text{Prob}}\!\left(X\leq x\right)}$

Функция является унимодальной , если она монотонно возрастает до некоторой точки ( моды ), а затем монотонно убывает.

Когда — строго монотонная функция, то инъективна на своей области определения, а если — область значений , то существует обратная функция на для . Напротив, каждая постоянная функция является монотонной, но не инъективной ^{[7] и, следовательно} , не может иметь обратную.${\displaystyle f}$${\displaystyle f}$${\displaystyle T}$${\displaystyle f}$${\displaystyle T}$${\displaystyle f}$

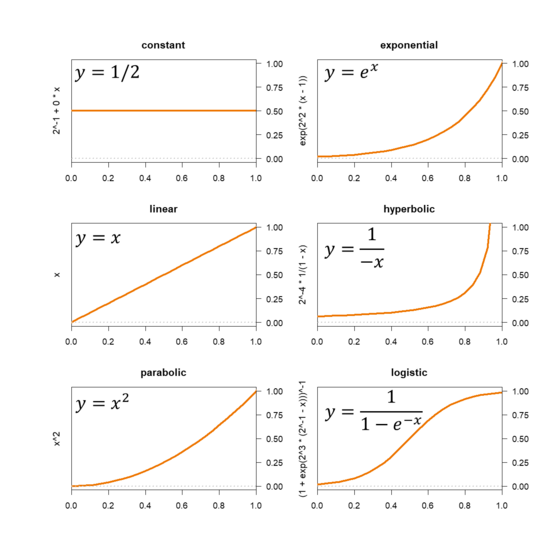
На графике показаны шесть монотонных функций. Их простейшие формы показаны в области графика, а выражения, используемые для их создания, показаны на оси Y.

Говорят, что отображение монотонно , если каждый из его слоев связен ; то есть для каждого элемента множество (возможно пустое) является связным подпространством${\displaystyle f:X\to Y}$${\displaystyle y\in Y,}$${\displaystyle f^{-1}(y)}$${\displaystyle X.}$

В функциональном анализе на топологическом векторном пространстве оператор (возможно, нелинейный) называется монотонным, если${\displaystyle X}$${\displaystyle T:X\rightarrow X^{*}}$

$${\displaystyle (Tu-Tv,u-v)\geq 0\quad \forall u,v\in X.}$$Теорема Качуровского показывает, что выпуклые функции на банаховых пространствах имеют своими производными монотонные операторы.

Подмножество называется монотонным множеством, если для каждой пары и в ,${\displaystyle G}$${\displaystyle X\times X^{*}}$${\displaystyle [u_{1},w_{1}]}$${\displaystyle [u_{2},w_{2}]}$${\displaystyle G}$

$${\displaystyle (w_{1}-w_{2},u_{1}-u_{2})\geq 0.}$$${\displaystyle G}$называется максимально монотонным, если он является максимальным среди всех монотонных множеств в смысле включения множеств. График монотонного оператора является монотонным множеством. Монотонный оператор называется максимально монотонным, если его график является максимальным монотонным множеством .${\displaystyle G(T)}$

Теория порядка имеет дело с произвольными частично упорядоченными множествами и предупорядоченными множествами как обобщением действительных чисел. Приведенное выше определение монотонности применимо и в этих случаях. Однако термины «возрастающий» и «убывающий» избегаются, поскольку их обычное графическое представление не применимо к порядкам, которые не являются тотальными . Кроме того, строгие отношения и малопригодны во многих не тотальных порядках, и поэтому для них не вводится дополнительная терминология.${\displaystyle <}$${\displaystyle >}$

Пусть обозначает отношение частичного порядка любого частично упорядоченного множества, монотонную функцию, также называемую изотонной , или${\displaystyle \leq }$порядок-сохраняющий , удовлетворяет свойство

$${\displaystyle x\leq y\implies f(x)\leq f(y)}$$

для всех x и y в его области определения. Композиция двух монотонных отображений также монотонна.

Двойственное понятие часто называют антитонным , антимонотонным или обращающим порядок . Следовательно, антитонная функция f удовлетворяет свойству

$${\displaystyle x\leq y\implies f(y)\leq f(x),}$$

для всех x и y в его области определения.

Постоянная функция является как монотонной, так и антитонной; и наоборот, если f является как монотонной, так и антитонной, и если область определения f представляет собой решетку , то f должна быть постоянной.

Монотонные функции являются центральными в теории порядка. Они появляются в большинстве статей по этой теме, и примеры из специальных приложений можно найти в этих местах. Некоторые примечательные специальные монотонные функции являются вложениями порядка (функции, для которых тогда и только тогда , когда и изоморфизмы порядка ( сюръективные вложения порядка).${\displaystyle x\leq y}$ ${\displaystyle f(x)\leq f(y))}$

В контексте алгоритмов поиска монотонность (также называемая согласованностью) — это условие, применяемое к эвристическим функциям . Эвристика является монотонной, если для каждого узла n и каждого преемника n' из n, сгенерированного любым действием a , предполагаемая стоимость достижения цели из n не превышает стоимости шага для достижения n' плюс предполагаемая стоимость достижения цели из n' ,${\displaystyle h(n)}$

$${\displaystyle h(n)\leq c\left(n,a,n'\right)+h\left(n'\right).}$$

Это форма неравенства треугольника с n , n' и целью G _{n ,} наиболее близкой к n . Поскольку каждая монотонная эвристика также допустима , монотонность является более строгим требованием, чем допустимость. Некоторые эвристические алгоритмы, такие как A*, могут быть доказаны оптимальными при условии, что используемая ими эвристика является монотонной. ^[8]

В булевой алгебре монотонная функция — это такая, что для всех a _i и b _i в {0,1} , если a ₁ ≤ b ₁ , a ₂ ≤ b ₂ , ..., an ≤ b _n (т. е. декартово произведение {0, 1} ⁿ _{упорядочено} покоординатно ) , то f( a ₁ , ..., an ₎ ≤ f( b ₁ , ..., b _n ) . Другими словами, булева функция монотонна, если для каждой комбинации входов переключение одного из входов с false на true может вызвать только переключение выхода с false на true, а не с true на false. Графически это означает, что n -арная булева функция монотонна, когда ее представление в виде n -мерного куба, помеченного значениями true, не имеет восходящего ребра от true к false . (Эта помеченная диаграмма Хассе является двойственной помеченной диаграмме Венна функции , которая является более распространенным представлением для n ≤ 3. )

Монотонные булевы функции — это именно те, которые можно определить выражением, объединяющим входные данные (которые могут появляться более одного раза) с использованием только операторов and и or (в частности, not запрещено). Например, «не менее двух из a , b , c удерживаются» — это монотонная функция a , b , c , поскольку ее можно записать, например, как (( a и b ) или ( a и c ) или ( b и c )).

Число таких функций от n переменных известно как число Дедекинда от n .

Решение SAT , как правило, NP-сложной задачи, может быть достигнуто эффективно, когда все задействованные функции и предикаты являются монотонными и булевыми. ^[9]

• Монотонная кубическая интерполяция
• Псевдомонотонный оператор
• Коэффициент ранговой корреляции Спирмена — мера монотонности в наборе данных
• Полная монотонность
• Циклическая монотонность
• Операторная монотонная функция
• Функция монотонного набора
• Абсолютно и полностью монотонные функции и последовательности

• Бартл, Роберт Г. (1976). Элементы реального анализа (второе изд.).
• Гретцер, Джордж (1971). Теория решеток: первые концепции и распределительные решетки . WH Freeman. ISBN 0-7167-0442-0.
• Пембертон, Малкольм; Рау, Николас (2001). Математика для экономистов: вводный учебник . Manchester University Press. ISBN 0-7190-3341-1.
• Ренарди, Майкл и Роджерс, Роберт К. (2004). Введение в уравнения с частными производными . Тексты по прикладной математике 13 (Второе изд.). Нью-Йорк: Springer-Verlag. С. 356. ISBN 0-387-00444-0.
• Рис, Фридьес и Бела Секефальви-Надь (1990). Функциональный анализ . Публикации Курьера Дувра. ISBN 978-0-486-66289-3.
• Рассел, Стюарт Дж.; Норвиг, Питер (2010). Искусственный интеллект: современный подход (3-е изд.). Upper Saddle River, Нью-Джерси: Prentice Hall. ISBN 978-0-13-604259-4.
• Саймон, Карл П.; Блюм, Лоуренс (апрель 1994 г.). Математика для экономистов (первое издание). Нортон. ISBN 978-0-393-95733-4.(Определение 9.31)

• «Монотонная функция», Энциклопедия математики , EMS Press , 2001 [1994]
• Сходимость монотонной последовательности Аник Дебнат и Томаса Роксло (Школа Харкера), Демонстрационный проект Вольфрама .
• Вайсштейн, Эрик В. "Монотонная функция". MathWorld .