Список евклидовых однородных мозаик

В этой таблице показаны 11 выпуклых однородных мозаик (правильных и полуправильных) евклидовой плоскости и их двойственные мозаики.

На плоскости есть три правильных и восемь полуправильных мозаик . Полуправильные мозаики образуют новые мозаики из своих двойственных мозаик, каждая из которых сделана из одного типа неправильной грани.

Джон Конвей назвал эти однородные двойственные мозаики каталонскими мозаиками , параллельными каталонским телесным многогранникам.

Однородные плитки перечислены по конфигурации вершин , последовательности граней, которые существуют на каждой вершине. Например, 4.8.8 означает один квадрат и два восьмиугольника на вершине.

Эти 11 однородных мозаик имеют 32 различных однородных окраски . Однородная окраска позволяет по-разному раскрашивать многоугольники с одинаковыми сторонами в вершине, сохраняя при этом однородность вершин и трансформационную конгруэнтность между вершинами. (Примечание: некоторые из изображений мозаик, показанных ниже, не являются однородными по цвету.)

В дополнение к 11 выпуклым однородным мозаикам, также известны 14 невыпуклых мозаик , использующих звездчатые многоугольники и конфигурации вершин с обратной ориентацией. Еще 28 однородных мозаик известны с использованием апейрогонов . Если также допускаются зигзаги, то известны еще 23 однородных мозаики и еще 10 известных семейств в зависимости от параметра: в 8 случаях параметр непрерывен, а в 2 других — дискретен. Известно, что набор не является полным.

В книге 1987 года « Мозаики и узоры » Бранко Грюнбаум называет вершинно-однородные мозаики архимедовыми , параллельными архимедовым телам . Их двойственные мозаики называются мозаиками Лавеса в честь кристаллографа Фрица Лавеса . ^{[1] [2]} Их также называют мозаиками Шубникова–Лавеса в честь Алексея Шубникова . ^[3] Джон Конвей назвал однородные двойственные мозаики каталонскими мозаиками , параллельными каталоновым телам .

У мозаик Лавеса вершины находятся в центрах правильных многоугольников, а ребра соединяют центры правильных многоугольников, имеющих общее ребро. Плитки мозаик Лавеса называются планигонами . Сюда входят 3 правильные плитки (треугольник, квадрат и шестиугольник) и 8 неправильных. ^[4] Каждая вершина имеет ребра, равномерно расположенные вокруг нее. Трехмерные аналоги планигонов называются стереоэдрами .

Эти двойные плитки перечислены по их конфигурации граней , количеству граней в каждой вершине грани. Например, V4.8.8 означает равнобедренные треугольные плитки с одним углом с четырьмя треугольниками и двумя углами, содержащими восемь треугольников. Ориентации планигонов вершин (до D ₁₂ ) соответствуют диаграммам вершин в следующих разделах.

Одиннадцать планигонов

Треугольники				Четырехугольники			Пентагоны			Шестиугольник
В6 3	В4.8 2	В4.6.12	В3.12 2	В4 4	В(3,6) 2	В3.4.6.4	В3 2 .4.3.4	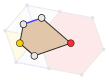В3 4 .6	В3 3 .4 2	В3 6

Все отражательные формы могут быть созданы с помощью построений Витхоффа , представленных символами Витхоффа или диаграммами Коксетера-Дынкина , каждая из которых работает над одним из трех треугольников Шварца (4,4,2), (6,3,2) или (3,3,3), с симметрией, представленной группами Коксетера : [4,4], [6,3] или [3 ^[3] ]. Альтернативные формы, такие как курносая, также могут быть представлены специальными разметками в каждой системе. Только одна однородная мозаика не может быть построена с помощью процесса Витхоффа, но может быть создана путем удлинения треугольной мозаики. Также существует ортогональная зеркальная конструкция [∞,2,∞], рассматриваемая как два набора параллельных зеркал, образующих прямоугольную фундаментальную область. Если область квадратная, эта симметрия может быть удвоена диагональным зеркалом в семейство [4,4].

Семьи:

• (4,4,2), , [4,4] – Симметрия правильной квадратной мозаики${\displaystyle {\tilde {BC}}_{2}}$
  • ${\displaystyle {\tilde {I}}_{1}^{2}}$, [∞,2,∞]
• (6,3,2), , [6,3] – Симметрия правильной шестиугольной мозаики и треугольной мозаики .${\displaystyle {\тильда {G}}_{2}}$
  • (3,3,3), , [3 ^[3] ]${\displaystyle {\тильда {A}}_{2}}$

Однородные мозаики (Платоновы и Архимедовы)	Вершинная фигура и символ(ы) Витхоффа Группа симметрии Диаграмма (ы) Коксетера	Двойственно -однородные мозаики (называемые мозаиками Лавеса или Каталонскими мозаиками)
Квадратная мозаика (кадриль)	4.4.4.4 (или 4 4 ) 4 | 2 4 п4м , [4,4], (*442)	самодвойной (кадриль)
Усеченная квадратная мозаика (усеченная кадриль)	4.8.8 2 | 4 4 4 4 2 | п4м , [4,4], (*442) или	Квадратная мозаика Тетракис (kisquadrille)
Плосконосая квадратная мозаика (плосконосая кадриль)	3.3.4.3.4 | 4 4 2 p4g , [4 + ,4], (4*2) или	Пятиугольная мозаика Каира (4-кратная пентилья)

Платоновы и архимедовы мозаики	Вершинная фигура и символ(ы) Витхоффа Группа симметрии Диаграмма (ы) Коксетера	Двойные мозаики Лавеса
Шестиугольная мозаика (гекстилле)	6.6.6 (или 6 3 ) 3 | 6 2 2 6 | 3 3 3 3 | п6м , [6,3], (*632)	Треугольная мозаика (дельтиль)
Тригексагональная мозаика (гексадельтиль)	(3.6) 2 2 | 6 3 3 3 | 3 п6м , [6,3], (*632) =	Ромбическая мозаика (ромб)
Усеченная шестиугольная мозаика (усеченный гексагон)	3.12.12 2 3 | 6 п6м , [6,3], (*632)	Треугольная мозаика Triakis (kisdeltille)
Треугольная мозаика (дельтиль)	3.3.3.3.3.3 (или 3 6 ) 6 | 3 2 3 | 3 3 | 3 3 3 п6м , [6,3], (*632) =	Шестиугольная мозаика (гекстилле)
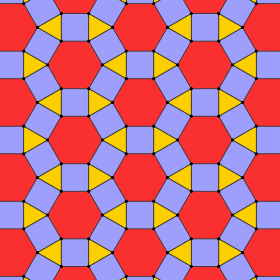Ромботригексагональная мозаика (rhombihexadeltille)	3.4.6.4 3 | 6 2 п6м , [6,3], (*632)	Дельтовидная тригексагональная мозаика (тетрил)
Усеченная тригексагональная мозаика (усеченный гексадельтиль)	4.6.12 2 6 3 | p6m , [6,3], (*632)	Кисромбилльная мозаика (кисромбилле)
Плосконосая тригексагональная мозаика (плосконосый гексагон)	3.3.3.3.6 | 6 3 2 p6 , [6,3] + , (632)	Пятиугольная мозаика «Флорет» (6-кратная пентилья)

Платоновы и архимедовы мозаики	Вершинная фигура и символ(ы) Витхоффа с двойной гранью Группа симметрии Диаграмма Коксетера	Двойные мозаики Лавеса
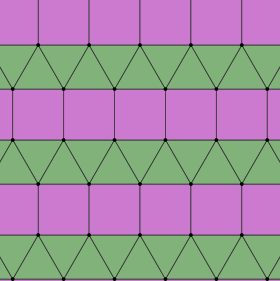Удлиненная треугольная мозаика (равноплоскостная квадратная мозаика)	3.3.3.4.4 2 | 2 (2 2) см , [∞,2 + ,∞], (2*22)	Призматическая пентагональная мозаика (изо(4-)пентил)

Всего существует 32 варианта однородной раскраски 11 однородных мозаик:

1. Треугольная мозаика – 9 однородных раскрасок, 4 витхоффовых, 5 невитхоффовых
   •          
2. Квадратная мозаика – 9 раскрасок: 7 витхоффовых, 2 невитхоффовых
   •          
3. Шестиугольная мозаика – 3 раскраски, все витхоффовы
   •    
4. Тригексагональная мозаика – 2 раскраски, обе витхоффовы
   •   
5. Мозаика из плосконосых квадратов – 2 раскраски, обе чередующиеся витхоффовские
   •   
6. Усеченная квадратная мозаика – 2 раскраски, обе витхоффовские
   •   
7. Усеченная шестиугольная мозаика – 1 раскраска, витхоффовская
   •  
8. Ромботригексагональная мозаика – 1 раскраска, витхоффовская
   •  
9. Усеченная тригексагональная мозаика – 1 раскраска, витхоффовская
   •  
10. Плосконосая шестиугольная мозаика – 1 раскраска, чередующаяся по Витхоффу
    •  
11. Удлиненная треугольная мозаика – 1 раскраска, невитхоффова
    •  

• Выпуклые однородные соты – 28 однородных 3-мерных мозаик, параллельная конструкция выпуклых однородных мозаик евклидовой плоскости.
• Евклидовы мозаики выпуклыми правильными многоугольниками
• Список тесселяций
• Порог просачивания
• Однородные мозаики на гиперболической плоскости

• Conway, John H .; Burgiel, Heidi; Goodman-Strauss, Chaim (18 апреля 2008 г.). "Глава 19, Archimedean tilings , table 19.1". Симметрии вещей. AK Peters / CRC Press . ISBN 978-1-56881-220-5. Архивировано из оригинала 19 сентября 2010 года.
• Коксетер, Х. С. М .; Лонге-Хиггинс, М. С .; Миллер, Дж. С. П. (1954). «Однородные многогранники». Phil. Trans. 246 A: 401– 450.
• Уильямс, Роберт (1979). Геометрическая основа естественной структуры: первоисточник дизайна . Dover Publications, Inc. ISBN 0-486-23729-X.(Раздел 2–3 Упаковки кругов, плоские мозаики и сети , стр. 34–40).
• Асаро, Лора; Хайд, Джон; Дженсен, Мелани; Манн, Кейси; Шредер, Тайлер. «Однородная раскраска рёбер c архимедовых мозаик» (PDF) . Вашингтонский университет .(Кейси Манн из Вашингтонского университета)
• Грюнбаум, Бранко ; Шепард, Джеффри (ноябрь 1977 г.). «Замощения правильными многоугольниками» (PDF) .
• Сеймур, Дейл; Бриттон, Джилл (1989). Введение в тесселяции. Dale Seymour Publications. стр. 50–57, 71-74. ISBN 978-0866514613.

• Вайсштейн, Эрик В. «Равномерная тесселяция». MathWorld .
• Равномерные замощения на плоскости Евклида
• Мозаики плоскости
• Мир тесселяций Дэвида Бейли
• k-однородные мозаики
• n-однородные мозаики