Усеченная тригексагональная мозаика

Усеченная тригексагональная мозаика
Тип	Полуправильная мозаика
Конфигурация вершины	4.6.12
Символ Шлефли	тр{6,3} или${\displaystyle t{\begin{Bmatrix}6\\3\end{Bmatrix}}}$
Символ Витхоффа	2 6 3 |
Диаграмма Коксетера
Симметрия	п6м , [6,3], (*632)
Симметрия вращения	р6 , [6,3] + , (632)
Акроним Bowers	Другой
Двойной	Мозаика Kisrhombille
Характеристики	Вершинно-транзитивный

В геометрии усеченная тригексагональная мозаика — одна из восьми полуправильных мозаик евклидовой плоскости. На каждой вершине находится один квадрат , один шестиугольник и один двенадцатиугольник . Символ Шлефли — tr {3,6}.

Существует только одна однородная раскраска усеченной тригексагональной мозаики, грани которой окрашены сторонами многоугольников. 2-однородная раскраска имеет два цвета шестиугольников. 3-однородные раскраски могут иметь 3 цвета двенадцатиугольников или 3 цвета квадратов.

	1-униформа	2-единообразный	3-единообразный
Раскрашивание
Симметрия	п6м, [6,3], (*632)	p3m1, [3 [3] ], (*333)

Усеченная тригексагональная мозаика имеет три связанных 2-однородных мозаики , одна из которых является 2-однородной раскраской полуправильной ромботригексагональной мозаики . Первая рассекает шестиугольники на 6 треугольников. Две другие рассекают додекагоны на центральный шестиугольник и окружающие треугольники и квадрат в двух различных ориентациях. ^{[2] [3]}

Полурегулярный	Вскрытия	Полурегулярный	2-единообразный		3-единообразный
Двойной	Вставки

Усеченная тригексагональная мозаика может быть использована как упаковка кругов , размещая круги одинакового диаметра в центре каждой точки. Каждый круг находится в контакте с 3 другими кругами в упаковке ( целующееся число ). ^[4]

Мозаика Kisrhombille
Тип	Двойная полуправильная мозаика
Лица	треугольник 30-60-90
Диаграмма Коксетера
Группа симметрии	п6м, [6,3], (*632)
Группа вращения	р6, [6,3] + , (632)
Двойной многогранник	усеченная тригексагональная мозаика
Конфигурация лица	В4.6.12
Характеристики	фейс-транзитивный

Мозаика кисромбилла или 3-6 кисромбилла — это мозаика евклидовой плоскости. Она построена из конгруэнтных треугольников 30-60-90 с 4, 6 и 12 треугольниками, встречающимися в каждой вершине.

Разделение граней этих мозаик создает мозаику кисромбилла. (Сравните дисдиакис гекса- , додека- и триаконтаэдр , три каталонских тела , похожих на эту мозаику.)

• 
  3-6 дельтовидные
• 
  ромб
• 
  шестиугольный

Конвей называет его кисромбиллом ^[1] из-за его операции биссектрисы вершины kis , примененной к ромбической мозаике . Более конкретно, ее можно назвать 3-6 кисромбиллом , чтобы отличать ее от других подобных гиперболических мозаик, таких как 3-7 кисромбилл .

Его можно рассматривать как равностороннюю шестиугольную мозаику , в которой каждый шестиугольник разделен на 12 треугольников из центральной точки. (В качестве альтернативы его можно рассматривать как треугольную мозаику, разделенную пополам на 6 треугольников, или как бесконечное расположение линий в шести параллельных семействах.)

Он обозначен как V4.6.12, поскольку каждая грань прямоугольного треугольника имеет три типа вершин: одну с 4 треугольниками, одну с 6 треугольниками и одну с 12 треугольниками.

Треугольники мозаики кисромбилла представляют собой фундаментальные домены симметрии группы обоев p6m, [6,3] (*632 орбифолдная нотация ) . Существует ряд малых подгрупп индексов, построенных из [6,3] путем зеркального удаления и чередования. [1 ⁺ ,6,3] создает симметрию *333, показанную красными зеркальными линиями. [6,3 ⁺ ] создает симметрию 3*3. [6,3] ⁺ является вращательной подгруппой. Подгруппа коммутатора - [1 ⁺ ,6,3 ⁺ ], которая является симметрией 333. Более крупная подгруппа индекса 6, построенная как [6,3*], также становится (*333), показанной синими зеркальными линиями, и которая имеет свою собственную вращательную симметрию 333, индекс 12.

Малые индексные подгруппы [6,3] (*632)
Индекс	1	2		3	6
Диаграмма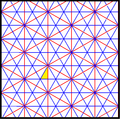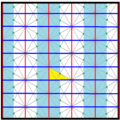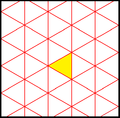
Международный ( орб. ) Коксетер	п6м (*632) [6,3] ==	p3m1 ( *333 ) [1 + ,6,3] ==	п31м (3*3) [6,3 + ] =	смм (2*22)	пмм ( *2222 )	p3m1 ( *333 ) [6,3*] ==
Прямые подгруппы
Индекс	2	4		6	12
Диаграмма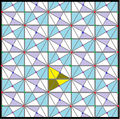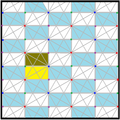
Международный (орб.) Коксетер	стр6 (632) [6,3] + ==	р3 (333) [1 + ,6,3 + ] ==		стр2 (2222)	стр2 (2222)	р3 (333) [1 + ,6,3*] ==

Существует восемь однородных мозаик , которые могут быть основаны на правильной шестиугольной мозаике (или двойной треугольной мозаике ). Рисуя плитки, окрашенные в красный цвет на исходных гранях, в желтый цвет на исходных вершинах и в синий цвет вдоль исходных ребер, получаем 8 форм, 7 из которых топологически различны. ( Усеченная треугольная мозаика топологически идентична шестиугольной мозаике.)

Однородные шестиугольные/треугольные мозаики в т е
Симметрия : [6,3], (*632)							[6,3] + (632)	[6,3 + ] (3*3)
{6,3}	т{6,3}	г{6,3}	т{3,6}	{3,6}	рр{6,3}	тр{6,3}	ср{6,3}	с{3,6}
6 3	3.12 2	(3,6) 2	6.6.6	3 6	3.4.6.4	4.6.12	3.3.3.3.6	3.3.3.3.3.3
Равномерные дуалы
В6 3	В3.12 2	В(3,6) 2	В6 3	В3 6	В3.4.6.4	В.4.6.12	В3 4 .6	В3 6

Эту мозаику можно считать членом последовательности однородных узоров с вершинной фигурой (4.6.2p) и диаграммой Коксетера-Дынкина . При p < 6 членами последовательности являются всеусеченные многогранники ( зоноэдры ), показанные ниже как сферические мозаики. При p > 6 они являются мозаиками гиперболической плоскости, начиная с усеченной тригептагональной мозаики .

* n 32 мутация симметрии усеченных мозаик: 4.6.2 n в т е
Сим. * н 32 [ н ,3]	Сферический				Евклид.	Компактный гиперб.		Парако.	Некомпактный гиперболический
	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]	*∞32 [∞,3]	[12i,3]	[9и,3]	[6i,3]	[3и,3]
Цифры
Конфигурация.	4.6.4	4.6.6	4.6.8	4.6.10	4.6.12	4.6.14	4.6.16	4.6.∞	4.6.24i	4.6.18i	4.6.12i	4.6.6i
Двойные
Конфигурация.	В4.6.4	В4.6.6	В4.6.8	В4.6.10	В4.6.12	В4.6.14	В4.6.16	В4.6.∞	V4.6.24i	V4.6.18i	V4.6.12i	V4.6.6i

На Викискладе есть медиафайлы по теме « Однородная мозаика 4-6-12 (усеченная тригексагональная мозаика)» .

• Мозаики правильных многоугольников
• Список однородных мозаик

• Уильямс, Роберт (1979). Геометрическая основа естественной структуры: путеводитель по дизайну . Dover Publications, Inc. стр. 41. ISBN 0-486-23729-X.
• Джон Х. Конвей, Хайди Берджил, Хаим Гудман-Штраус, Симметрии вещей 2008, ISBN 978-1-56881-220-5 [1] 
• Кейт Кричлоу, «Порядок в пространстве: справочник по дизайну» , 1970, стр. 69-61, Pattern G, Dual, стр. 77-76, pattern 4
• Дейл Сеймур и Джилл Бриттон , Введение в тесселяцию , 1989, ISBN 978-0866514613 , стр. 50–56 

• Вайсштейн, Эрик В. «Равномерная тесселяция». MathWorld .
• Вайсштейн, Эрик В. «Полурегулярная мозаика». MathWorld .
• Клитцинг, Ричард. «Двумерные евклидовы мозаики x3x6x - othat - O9».