Стереоэдр

В геометрии и кристаллографии стереоэдр — это выпуклый многогранник , который заполняет пространство изоэдрально , что означает, что симметрии мозаики переводят любую копию стереоэдра в любую другую копию.

Двумерные аналоги стереоэдров называются планигонами . Многогранники более высокой размерности также могут быть стереоэдрами, хотя их было бы точнее называть стереотопами .

Подмножество стереоэдров называется плезиоэдрами и определяется как ячейки Вороного симметричного множества Делоне .

Параллелоэдры — это плезиоэдры, заполняющие пространство только путем трансляции. Ребра здесь окрашены как параллельные векторы.

Параллелоэдры

куб	шестиугольная призма	ромбический додекаэдр	удлиненный додекаэдр	усеченный октаэдр

Катоптрическая мозаика содержит ячейки стереоэдров. Двугранные углы являются целыми делителями 180° и окрашены в соответствии с их порядком. Первые три являются фундаментальными областями симметрии , , и , представленными диаграммами Коксетера-Дынкина :${\displaystyle {\тильда {C}}_{3}}$${\displaystyle {\тильда {B}}_{3}}$${\displaystyle {\тильда {A}}_{3}}$,и. является полусимметрией , а является четвертной симметрией.${\displaystyle {\тильда {B}}_{3}}$${\displaystyle {\тильда {C}}_{3}}$${\displaystyle {\тильда {A}}_{3}}$

Любые заполняющие пространство стереоэдры с элементами симметрии могут быть разрезаны на меньшие идентичные ячейки, которые также являются стереоэдрами. Модификаторы имени ниже, половина, четверть и восьмая представляют такие разбиения.

Катоптрические клетки

Лица	4				5			6				8	12
Тип	Тетраэдры				Квадратная пирамида			Треугольная бипирамида		Куб		Октаэдр	Ромбический додекаэдр
Изображения	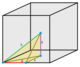1/48 (1)	1/24 (2)	1/12 (4)	1/12 (4)	1/24 (2)	1/6 (8)	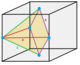1/6 (8)	1/12 (4)	1/4 (12)	1 (48)	1/2 (24)	1/3 (16)	2 (96)
Симметрия (порядок)	С 1 1	С 1в 2	Д 2д 4	С 1в 2	С 1в 2	С 4v 8	С 2в 4	С 2в 4	С 3в 6	О ч 48	Д 3д 12	Д 4ч 16	О ч 48
Соты	Восьмая пирамидка	Треугольная пирамидка	Сплюснутый тетраэдр	Половина пирамиды	Квадратная четверть пирамидилла	Пирамидиллия	Полусплюснутый октаэдр	Четверть сплющенный октаэдр	четверть кубилья	Кубиль	сплющенный кубиль	сплющенный октаэдр	Додекаэдр

Другие выпуклые многогранники, которые являются стереоэдрами, но не параллелоэдрами или плезиоэдрами, включают гиробифастигиум .

Другие

Лица	8		10	12
Симметрия (порядок)	Д 2д (8)			Д 4ч (16)
Изображения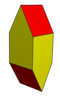
Клетка	Гиробифастигиум	Удлиненный гиробифастигиум	Десятка бубен	Удлиненная квадратная бипирамида

• Иванов, А.Б. (2001) [1994], "Стереоэдр", Энциклопедия математики , Издательство EMS
• Б. Н. Делоне , Н. Н. Сандакова, Теория стереоэдров, Труды Матем. ин-та МАТЕМАТИЧЕСКОГО ИНСТИТУТА ...
• Голдберг, Майкл Три бесконечных семейства тетраэдрических заполнителей пространства Журнал комбинаторной теории A, 16, стр. 348–354, 1974.
• Голдберг, Майкл Пятигранники, заполняющие пространство , Журнал комбинаторной теории, Серия A Том 13, Выпуск 3, Ноябрь 1972, Страницы 437-443 [1] PDF
• Голдберг, Майкл Пентаэдры, заполняющие пространство II , Журнал комбинаторной теории 17 (1974), 375–378. PDF
• Голдберг, Майкл О гексаэдрах, заполняющих пространство Geom. Dedicata, июнь 1977 г., том 6, выпуск 1, стр. 99–108 [2] PDF
• Голдберг, Майкл О заполняющих пространство семигранниках Geometriae Dedicata, июнь 1978 г., том 7, выпуск 2, стр. 175–184 [3] PDF
• Голдберг, Майкл Выпуклые многогранные заполнители пространства с более чем двенадцатью гранями. Geom. Dedicata 8, 491-500, 1979.
• Голдберг, Майкл О заполняющих пространство октаэдрах , Geometriae Dedicata, январь 1981 г., том 10, выпуск 1, стр. 323–335 [4] PDF
• Голдберг, Майкл О заполняющих пространство декаэдрах . Структурная топология, 1982, номер. Тип 10-II PDF
• Голдберг, Майкл О заполняющих пространство эннеаэдрах Geometriae Dedicata, июнь 1982 г., том 12, выпуск 3, стр. 297–306 [5] PDF