6-кубовый

6-мерный гиперкуб

6-кубовый гексагональный
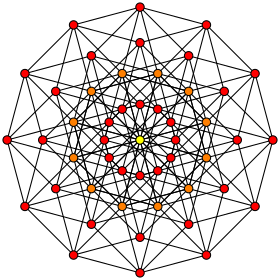Ортогональная проекция внутри многоугольника Петри. Оранжевые вершины удвоены, а центральная желтая вершина имеет 4 вершины.
Тип	Правильный 6-мерный многогранник
Семья	гиперкуб
Символ Шлефли	{4,3 ⁴ }
Диаграмма Коксетера
5-гранный	12 {4,3,3,3}
4-х гранный	60 {4,3,3}
Клетки	160 {4,3}
Лица	240 {4}
Края	192
Вершины	64
Вершинная фигура	5-симплекс
Петри полигон	двенадцатиугольник
Группа Коксетера	Б ₆ , [3 ⁴ ,4]
Двойной	6-ортоплекс
Характеристики	выпуклый , многогранник Ганнера

В геометрии 6 -куб — это шестимерный гиперкуб с 64 вершинами , 192 ребрами , 240 квадратными гранями , 160 кубическими ячейками , 60 4-гранями тессеракта и 12 5-гранями 5- куба .

Он имеет символ Шлефли {4,3 ⁴ }, состоящий из 3 5-кубов вокруг каждой 4-грани. Его можно назвать гексерактом , портманто тессеракта ( 4 -куба ) с гексом для шести (измерений) по -гречески . Его также можно назвать правильным додека-6-топом или додекапетоном , будучи 6-мерным многогранником, построенным из 12 правильных граней .

Связанные многогранники

Он является частью бесконечного семейства многогранников, называемых гиперкубами . Двойственный 6-кубу может быть назван 6-ортоплексом и является частью бесконечного семейства кросс-многогранников . Он состоит из различных 5-кубов , расположенных под перпендикулярными углами к оси u, образуя координаты (x,y,z,w,v,u). ^[1]^[2]

Применение операции чередования , удаляющей чередующиеся вершины 6-куба, создает еще один однородный многогранник , называемый 6-демикубом (часть бесконечного семейства, называемого полугиперкубами ), который имеет 12 5-демикубических и 32 5-симплексных граней.

Как конфигурация

Эта матрица конфигурации представляет 6-куб. Строки и столбцы соответствуют вершинам, ребрам, граням, ячейкам, 4-граням и 5-граням. Диагональные числа говорят, сколько элементов каждого элемента встречается во всем 6-кубе. Недиагональные числа говорят, сколько элементов столбца встречается в элементе строки или рядом с ним. ^[3]^[4]

${\begin{bmatrix}{\begin{matrix}64&6&15&20&15&6\\2&192&5&10&10&5\\4&4&240&4&6&4\\8&12&6&160&3&3\\16&32&24&8&60&2\\32&80&80&40&10&12\end{matrix}}\end{bmatrix}}$

Декартовы координаты

Декартовы координаты вершин 6-гранного куба с центром в начале координат и длиной ребра 2 равны

(±1,±1,±1,±1,±1,±1)

в то время как внутренняя часть состоит из всех точек (x ₀ , x ₁ , x ₂ , x ₃ , x ₄ , x ₅ ) с −1 < x _i < 1.

Строительство

Существует три группы Коксетера, связанные с 6-кубом, одна регулярная , с группой Коксетера C ₆ или [4,3,3,3,3] , и группа Коксетера с половинной симметрией (D ₆ ) или [3 ^3,1,1 ]. Конструкция самой низкой симметрии основана на гиперпрямоугольниках или пропризмах , декартовых произведениях гиперкубов меньшей размерности.

Имя	Шлефли	Симметрия	Заказ
Обычный 6-кубовый	{4,3,3,3,3}	[4,3,3,3,3]	46080
Квазирегулярный 6-куб		[3,3,3,3 ^1,1 ]	23040
гиперпрямоугольник	{4,3,3,3}×{}	[4,3,3,3,2]	7680
	{4,3,3}×{4}	[4,3,3,2,4]	3072
	{4,3} ²	[4,3,2,4,3]	2304
	{4,3,3}×{} ²	[4,3,3,2,2]	1536
	{4,3}×{4}×{}	[4,3,2,4,2]	768
	{4} ³	[4,2,4,2,4]	512
	{4,3}×{} ³	[4,3,2,2,2]	384
	{4} ² ×{} ²	[4,2,4,2,2]	256
	{4}×{} ⁴	[4,2,2,2,2]	128
	{} ⁶	[2,2,2,2,2]	64

Прогнозы

ортографические проекции
самолет Коксетера	Б ₆	Б ₅	Б ₄
График
Диэдральная симметрия	[12]	[10]	[8]
самолет Коксетера	Другой	Б ₃	Б ₂
График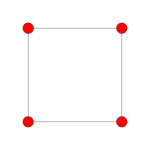
Диэдральная симметрия	[2]	[6]	[4]
самолет Коксетера		А ₅	А ₃
График
Диэдральная симметрия		[6]	[4]

3D-проекции
6-кубовое 6D простое вращение через 2Pi с 6D перспективной проекцией в 3D.	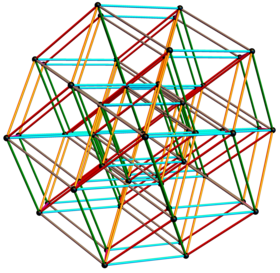Структура квазикристалла из 6 кубов, ортографически спроецированная в 3D с использованием золотого сечения .
Трехмерная перспективная проекция шестиугольника, совершающего тройное вращение вокруг ортогональных плоскостей X-W1, Y-W2 и Z-W3 .

Связанные многогранники

64 вершины 6-куба также представляют собой правильный косой 4-многогранник {4,3,4 | 4}. Его сеть можно рассматривать как матрицу 4×4×4 из 64 кубов, периодическое подмножество кубических сот , {4,3,4}, в 3-мерном пространстве. Он имеет 192 ребра и 192 квадратных грани. Противоположные грани складываются вместе в 4-цикл. Каждое направление сгиба добавляет 1 измерение, поднимая его до 6-пространства.

6-куб является 6-м в ряду гиперкубов :

Ортографические проекции полигонов Петри

Сегмент линии	Квадрат	Куб	4-кубовый	5-кубовый	6-кубовый	7-кубовый	8-кубовый	9-кубовый	10-кубовый

Этот многогранник является одним из 63 однородных 6-мерных многогранников, образованных из плоскости Коксетера _B6 , включая правильный 6-мерный куб или 6-ортоплекс .

Многогранники B6
β ₆	т ₁ β ₆	т ₂ β ₆	т ₂ γ ₆	т ₁ γ ₆	γ6	т _0,1 β ₆	т _0,2 β ₆
т _1,2 β ₆	т _0,3 β ₆	т _1,3 β ₆	т _2,3 γ ₆	т _0,4 β ₆	т _1,4 γ ₆	т _1,3 γ ₆	т _1,2 γ ₆
т _0,5 γ ₆	т _0,4 γ ₆	т _0,3 γ ₆	т _0,2 γ ₆	т _0,1 γ ₆	т _0,1,2 β ₆	т _0,1,3 β ₆	т _0,2,3 β ₆
т _1,2,3 β ₆	т _0,1,4 β ₆	т _0,2,4 β ₆	т _1,2,4 β ₆	т _0,3,4 β ₆	т _1,2,4 γ ₆	т _1,2,3 γ ₆	т _0,1,5 β ₆
т _0,2,5 β ₆	т _0,3,4 γ ₆	т _0,2,5 γ ₆	т _0,2,4 γ ₆	т _0,2,3 γ ₆	т _0,1,5 γ ₆	т _0,1,4 γ ₆	т _0,1,3 γ ₆
т _0,1,2 γ ₆	т _0,1,2,3 β ₆	т _0,1,2,4 β ₆	т _0,1,3,4 β ₆	т _0,2,3,4 β ₆	т _1,2,3,4 γ ₆	т _0,1,2,5 β ₆	т _0,1,3,5 β ₆
т _0,2,3,5 γ ₆	т _0,2,3,4 γ ₆	т _0,1,4,5 γ ₆	т _0,1,3,5 γ ₆	т _0,1,3,4 γ ₆	т _0,1,2,5 γ ₆	т _0,1,2,4 γ ₆	т _0,1,2,3 γ ₆
т _0,1,2,3,4 β ₆	т _0,1,2,3,5 β ₆	т _0,1,2,4,5 β ₆	т _0,1,2,4,5 γ ₆	т _0,1,2,3,5 γ ₆	т _0,1,2,3,4 γ ₆	т _0,1,2,3,4,5 γ ₆

Ссылки

^ "(PDF) Новая шестимерная гиперхаотическая система".
^ «Улучшенная операция проекции для цилиндрического алгебраического разложения трехмерного пространства — ScienceDirect».
^ Коксетер, Правильные многогранники, раздел 1.8 Конфигурации
^ Коксетер, Комплексные правильные многогранники, стр.117

Коксетер, HSM Regular Polytopes , (3-е издание, 1973), издание Dover, ISBN 0-486-61480-8 стр. 296, Таблица I (iii): Regular Polytopes, три regular polytopes в n-мерностях (n>=5)
Клитцинг, Ричард. «6D однородные многогранники (полипеты) o3o3o3o3o4x - ax».

Внешние ссылки

Вайсштейн, Эрик В. «Гиперкуб». MathWorld .
Ольшевский, Джордж. "Измерение многогранника". Глоссарий для гиперпространства . Архивировано из оригинала 4 февраля 2007 г.
Многомерный глоссарий: гиперкуб Гарретт Джонс

в т е Фундаментальные выпуклые правильные и однородные многогранники в размерностях 2–10
Семья	А _н	Б _н	Я ₂ (п) / Д _н	Е ₆ / Е ₇ / Е ₈ / Ф ₄ / Соль ₂	Н _н
Правильный многоугольник	Треугольник	Квадрат	п-гон	Шестиугольник	Пентагон
Однородный многогранник	Тетраэдр	Октаэдр • Куб	Демикуб		Додекаэдр • Икосаэдр
Равномерный полихорон	Пентахорон	16-ячеечный • Тессеракт	Демитессеракт	24-ячеечный	120-ячеечный • 600-ячеечный
Однородный 5-многогранник	5-симплекс	5-ортоплекс • 5-куб	5-демикуб
Однородный 6-многогранник	6-симплекс	6-ортоплекс • 6-куб	6-демикуб	1 ₂₂ • 2 ₂₁
Однородный 7-многогранник	7-симплекс	7-ортоплекс • 7-куб	7-демикуб	1 ₃₂ • 2 ₃₁ • 3 ₂₁
Однородный 8-многогранник	8-симплекс	8-ортоплекс • 8-куб	8-демикуб	1 ₄₂ • 2 ₄₁ • 4 ₂₁
Однородный 9-многогранник	9-симплекс	9-ортоплекс • 9-куб	9-демикуб
Однородный 10-многогранник	10-симплекс	10-ортоплекс • 10-куб	10-демикуб
Однородный n - многогранник	н - симплекс	n - ортоплекс • n - куб	н - демикуб	1 _к2 • 2 _к1 • к ₂₁	n - пятиугольный многогранник
Темы: Семейства многогранников • Правильный многогранник • Список правильных многогранников и соединений

[1] "(PDF) Новая шестимерная гиперхаотическая система".

[2] «Улучшенная операция проекции для цилиндрического алгебраического разложения трехмерного пространства — ScienceDirect».

[3] Коксетер, Правильные многогранники, раздел 1.8 Конфигурации

[4] Коксетер, Комплексные правильные многогранники, стр.117