Гиперпрямоугольник

Гиперпрямоугольник Ортотоп
Прямоугольный кубоид — это 3-ортотоп
Тип	Призма
Лица	2 н
Края	п × 2 п −1
Вершины	2 н
Символ Шлефли	{}×{}×···×{} = {} n [1]
Диаграмма Коксетера	···
Группа симметрии	[2 n −1 ] , порядок 2 n
Двойной многогранник	Прямоугольный n-фузилон
Характеристики	выпуклый , зоноэдр , изогональный

В геометрии гиперпрямоугольник (также называемый ящиком , гипербоксом , -ячейкой или ортотопом ^[2] ) является обобщением прямоугольника ( плоской фигуры ) и прямоугольного кубоида ( объемной фигуры ) на более высокие измерения . Необходимым и достаточным условием является то, что он конгруэнтен декартову произведению конечных интервалов . [ ^3] Это означает, что -мерное прямоугольное тело имеет каждое из своих ребер, равных одному из замкнутых интервалов, используемых в определении. Каждая -ячейка компактна . ^{[4] [5]}${\displaystyle k}$${\displaystyle k}$${\displaystyle k}$

Если все ребра имеют одинаковую длину, то это гиперкуб . Гиперпрямоугольник является частным случаем параллелоэдра .

Для каждого целого числа от до пусть и будут действительными числами такими, что . Множество всех точек, координаты которых удовлетворяют неравенствам, является -клеткой . ^[6]${\displaystyle i}$${\displaystyle 1}$${\displaystyle k}$${\displaystyle a_{i}}$${\displaystyle b_{i}}$${\displaystyle a_{i}<b_{i}}$${\displaystyle x=(x_{1},\dots ,x_{k})}$${\displaystyle \mathbb {R} ^{k}}$${\displaystyle a_{i}\leq x_{i}\leq b_{i}}$${\displaystyle k}$

Ячейка размерности особенно проста. Например, ячейка 1 — это просто интервал с . Ячейка 2 — это прямоугольник, образованный декартовым произведением двух замкнутых интервалов, а ячейка 3 — это прямоугольное тело. ${\displaystyle k}$${\displaystyle k\leq 3}$${\displaystyle [a,b]}$${\displaystyle a<b}$

Стороны и ребра 3 -ячейки не обязательно должны быть равны по (евклидовой) длине; хотя единичный куб (имеющий границы одинаковой евклидовой длины) является 3-ячейкой, множество всех 3-ячеек с ребрами одинаковой длины является строгим подмножеством множества всех 3-ячеек.${\displaystyle k}$

Четырехмерный ортотоп, скорее всего, является гиперкубоидом. ^[7]

Частным случаем n -мерного ортотопа, где все ребра имеют одинаковую длину, является n - куб или гиперкуб. ^[2]

По аналогии, термин «гиперпрямоугольник» может относиться к декартовым произведениям ортогональных интервалов других видов, таких как диапазоны ключей в теории баз данных или диапазоны целых чисел , а не действительных чисел . ^[8]

н -фузил
Пример: 3-фузил
Тип	Призма
Лица	2 н
Вершины	2 н
Символ Шлефли	{}+{}+···+{} = н {} [1]
Диаграмма Коксетера	...
Группа симметрии	[2 n −1 ] , порядок 2 n
Двойной многогранник	н- ортотоп
Характеристики	выпуклый , изотопный

Двойственный многогранник n -ортотопа по - разному назывался прямоугольным n -ортоплексом , ромбическим n -фузилем или n -ромбом . Он построен 2 n точками , расположенными в центре прямоугольных граней ортотопа.

Символ Шлефли n- фузиля можно представить в виде суммы n ортогональных отрезков: { } + { } + ... + { } или n { }.

1-фузея — это отрезок прямой . 2-фузея — это ромб . Его плоские поперечные выборки во всех парах осей — ромбы .

н	Пример изображения
1	Отрезок линии { }
2	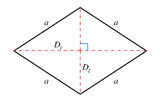Ромб { } + { } = 2{ }
3	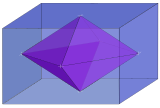Ромбический 3-ортоплекс внутри 3-ортотопа { } + { } + { } = 3{ }

• Минимальный ограничивающий прямоугольник
• Кубоид
• куб Гильберта

• Коксетер, Гарольд Скотт Макдональд (1973). Правильные многогранники (3-е изд.). Нью-Йорк: Довер. С. 122–123. ISBN 0-486-61480-8.

• Вайсштейн, Эрик В. «Ортотоп». MathWorld .
• Форан, Джеймс (1991-01-07). Основы реального анализа. CRC Press. ISBN 9780824784539. Получено 23 мая 2014 г.
• Рудин, Уолтер (1976). Принципы математического анализа . McGraw-Hill.