Геостационарная орбита
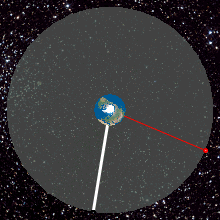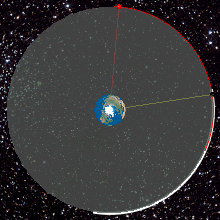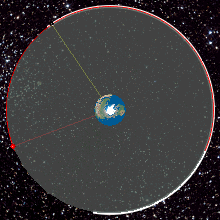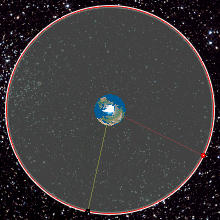

Геостационарная орбита , также называемая геосинхронной экваториальной орбитой [a] ( GEO ), представляет собой круговую геосинхронную орбиту высотой 35 786 км (22 236 миль) над экватором Земли , радиусом 42 164 км (26 199 миль) от центра Земли и следующей направлению вращения Земли .
Объект на такой орбите имеет орбитальный период, равный периоду вращения Земли, одному звездному дню , и поэтому для наземных наблюдателей он кажется неподвижным, в фиксированном положении на небе. Концепция геостационарной орбиты была популяризирована писателем-фантастом Артуром Кларком в 1940-х годах как способ революционизировать телекоммуникации, и первый спутник , размещенный на такой орбите, был запущен в 1963 году.
Спутники связи часто размещаются на геостационарной орбите, так что наземным спутниковым антеннам не нужно вращаться, чтобы отслеживать их, но они могут быть постоянно направлены на положение в небе, где находятся спутники. Метеорологические спутники также размещаются на этой орбите для мониторинга в реальном времени и сбора данных, а навигационные спутники — для предоставления известной точки калибровки и повышения точности GPS.
Геостационарные спутники запускаются через временную орбиту , а затем размещаются в «слоте» над определенной точкой на поверхности Земли. Спутнику требуется периодическое удержание на месте для сохранения своего положения. Современные выведенные из эксплуатации геостационарные спутники размещаются на более высокой орбите захоронения, чтобы избежать столкновений.
История

В 1929 году Герман Поточник описал как геосинхронные орбиты в целом, так и частный случай геостационарной орбиты Земли в частности как полезные орбиты для космических станций . [1] Первое упоминание геостационарной орбиты в популярной литературе было в октябре 1942 года в первой истории «Венера равносторонняя» Джорджа О. Смита , [2] но Смит не вдавался в подробности. Британский писатель-фантаст Артур К. Кларк популяризировал и расширил эту концепцию в статье 1945 года под названием «Внеземные ретрансляторы — могут ли ракетные станции обеспечить всемирное радиопокрытие?» , опубликованной в журнале Wireless World . Кларк признал эту связь во введении к «Полной Венере равносторонней» . [3] [4] Орбита, которую Кларк впервые описал как полезную для вещательных и ретрансляционных спутников связи, [4] иногда называется орбитой Кларка. [5] Аналогично, совокупность искусственных спутников на этой орбите известна как пояс Кларка. [6]
В технической терминологии орбита называется либо геостационарной, либо геосинхронной экваториальной орбитой, причем эти термины используются в некоторой степени взаимозаменяемо. [7]
Первый геостационарный спутник был разработан Гарольдом Розеном , когда он работал в Hughes Aircraft в 1959 году. Вдохновленный Спутником 1 , он хотел использовать геостационарный спутник для глобализации коммуникаций. Телекоммуникации между США и Европой тогда были возможны между всего 136 людьми одновременно и зависели от высокочастотных радиостанций и подводного кабеля . [8]
В то время считалось, что для размещения спутника на геостационарной орбите потребуется слишком много ракетной мощности, и он не просуществует достаточно долго, чтобы оправдать расходы, [9] поэтому первые усилия были направлены на созвездия спутников на низкой или средней околоземной орбите. [10] Первыми из них были пассивные спутники-шары Echo в 1960 году, за которыми последовал Telstar 1 в 1962 году. [11] Хотя эти проекты имели трудности с силой сигнала и отслеживанием, проблемы, которые можно было решить с помощью геостационарных орбит, концепция считалась непрактичной, поэтому Хьюз часто отказывал в финансировании и поддержке. [10] [8]
К 1961 году Розен и его команда создали цилиндрический прототип диаметром 76 сантиметров (30 дюймов), высотой 38 сантиметров (15 дюймов), весом 11,3 килограмма (25 фунтов), легкий и достаточно маленький, чтобы быть выведенным на орбиту. Он был стабилизирован вращением с помощью дипольной антенны, создающей луч в форме блина. [12] В августе 1961 года они были заключены контракт на начало строительства настоящего спутника. [8] Они потеряли Syncom 1 из-за отказа электроники, но Syncom 2 был успешно выведен на геосинхронную орбиту в 1963 году. Хотя его наклонная орбита все еще требовала перемещения антенн, он мог ретранслировать телевизионные передачи и позволил президенту США Джону Ф. Кеннеди в Вашингтоне, округ Колумбия, позвонить премьер-министру Нигерии Абубакару Тафаве Балеве на борту USNS Kingsport, пришвартованного в Лагосе 23 августа 1963 года. [10] [13]
Первым спутником, выведенным на геостационарную орбиту, был Syncom 3 , запущенный ракетой Delta D в 1964 году. [14] Благодаря увеличенной пропускной способности этот спутник смог транслировать прямую трансляцию летних Олимпийских игр из Японии в Америку. Геостационарные орбиты широко используются с тех пор, в частности, для спутникового телевидения. [10]
Сегодня существуют сотни геостационарных спутников, обеспечивающих дистанционное зондирование и связь. [8] [15]
Хотя большинство населенных пунктов на планете теперь имеют наземные средства связи ( микроволновые , оптоволоконные ), телефонный доступ охватывает 96% населения, а доступ в Интернет — 90%, [16] некоторые сельские и отдаленные районы в развитых странах по-прежнему зависят от спутниковой связи. [17] [18]
Использует
Большинство коммерческих спутников связи , вещательных спутников и спутников SBAS работают на геостационарных орбитах. [19] [20] [21]
Коммуникации
Геостационарные спутники связи полезны, поскольку они видны с большой площади поверхности Земли, простираясь на 81° по широте и 77° по долготе. [22] Они кажутся неподвижными в небе, что устраняет необходимость в наземных станциях иметь подвижные антенны. Это означает, что наземные наблюдатели могут устанавливать небольшие, дешевые и стационарные антенны, которые всегда направлены на нужный спутник. [23] : 537 Однако задержка становится значительной, поскольку для прохождения сигнала от наземного передатчика на экваторе до спутника и обратно требуется около 240 мс. [23] : 538 Эта задержка создает проблемы для чувствительных к задержке приложений, таких как голосовая связь, [24] поэтому геостационарные спутники связи в основном используются для однонаправленных развлечений и приложений, где альтернативы с низкой задержкой недоступны. [25]
Геостационарные спутники находятся прямо над головой на экваторе и кажутся ниже в небе для наблюдателя, находящегося ближе к полюсам. По мере увеличения широты наблюдателя связь становится более сложной из-за таких факторов, как атмосферная рефракция , тепловое излучение Земли , препятствия прямой видимости и отражения сигнала от земли или близлежащих сооружений. На широтах выше примерно 81° геостационарные спутники находятся ниже горизонта и вообще не видны. [22] Из-за этого некоторые российские спутники связи использовали эллиптические орбиты «Молния» и «Тундра» , которые имеют отличную видимость на высоких широтах. [26]
Метеорология
Всемирная сеть действующих геостационарных метеорологических спутников используется для предоставления видимых и инфракрасных изображений поверхности Земли и атмосферы для наблюдения за погодой, океанографии и атмосферного слежения. По состоянию на 2019 год в эксплуатации или в режиме ожидания находилось 19 спутников. [27] Эти спутниковые системы включают в себя:
- серия GOES США , управляемая NOAA [28]
- Серия Meteosat , запущенная Европейским космическим агентством и управляемая Европейской организацией метеорологических спутников, EUMETSAT [29]
- многоцелевые спутники COMS-1 и [30] GK-2A Республики Корея . [31]
- Российские спутники «Электро-Л»
- японский сериал Химавари [32]
- Китайская серия Фэнъюнь [33]
- Серия INSAT Индии [34]
Эти спутники обычно делают снимки в визуальном и инфракрасном спектре с пространственным разрешением от 0,5 до 4 квадратных километров. [35] Охват обычно составляет 70°, [35] а в некоторых случаях и меньше. [36]
Геостационарные спутниковые снимки использовались для отслеживания вулканического пепла , [37] измерения температуры верхней границы облаков и водяного пара, океанографии , [38] измерения температуры земли и растительного покрова, [39] [40] облегчения прогнозирования пути циклона , [34] и предоставления данных об облачности в реальном времени и других данных отслеживания. [41] Некоторая информация была включена в модели метеорологического прогнозирования , но из-за их широкого поля зрения, постоянного мониторинга и более низкого разрешения геостационарные метеорологические спутниковые снимки в основном используются для краткосрочного и реального прогнозирования. [42] [40]
Навигация

Геостационарные спутники могут использоваться для дополнения систем GNSS путем ретрансляции часов , эфемерид и поправок на ионосферные ошибки (рассчитанных с наземных станций известного местоположения) и предоставления дополнительного опорного сигнала. [43] Это повышает точность определения местоположения примерно с 5 м до 1 м или меньше. [44]
К прошлым и настоящим навигационным системам, использующим геостационарные спутники, относятся:
- Система широкополосного дополнения (WAAS), эксплуатируемая Федеральным управлением гражданской авиации США (FAA);
- Европейская геостационарная навигационная служба ( EGNOS ), управляемая ESSP (от имени GSA ЕС ) ;
- Многофункциональная спутниковая система дополнения (MSAS), эксплуатируемая Министерством земли, инфраструктуры и транспорта Японии ; Бюро гражданской авиации Японии (JCAB);
- Система GPS Aided Geo Augmented Navigation (GAGAN), эксплуатируемая Индией . [45] [46]
- Коммерческая навигационная система StarFire , эксплуатируемая компаниями John Deere и C-Nav Positioning Solutions ( Oceaneering );
- Коммерческая система Starfix DGPS и система OmniSTAR , эксплуатируемая Fugro . [47]
Выполнение
Запуск
Геостационарные спутники запускаются на восток на прямую орбиту, которая соответствует скорости вращения экватора. Наименьшее наклонение, на которое может быть запущен спутник, равно широте места запуска, поэтому запуск спутника из положения, близкого к экватору, ограничивает величину изменения наклона, которое потребуется позже. [48] Кроме того, запуск из положения, близкого к экватору, позволяет скорости вращения Земли придать спутнику ускорение. Место запуска должно иметь воду или пустыни на востоке, чтобы любые неудачные ракеты не упали на населенную территорию. [49]
Большинство ракет-носителей выводят геостационарные спутники непосредственно на геостационарную переходную орбиту (GTO), эллиптическую орбиту с апогеем на высоте GEO и низким перигеем . Затем бортовая двигательная установка спутника используется для подъема перигея, кругового движения и достижения GEO. [48] [50]
Распределение орбит
Спутники на геостационарной орбите должны все занимать одно кольцо над экватором . Требование разнести эти спутники, чтобы избежать вредных радиочастотных помех во время работы, означает, что доступно ограниченное количество орбитальных слотов, и, таким образом, только ограниченное количество спутников может работать на геостационарной орбите. Это привело к конфликту между разными странами, желающими получить доступ к одним и тем же орбитальным слотам (страны, находящиеся на одной долготе, но на разных широтах ) и радиочастотам . Эти споры решаются с помощью механизма распределения Международного союза электросвязи в соответствии с Регламентом радиосвязи . [51] [52] В Боготской декларации 1976 года восемь стран, расположенных на экваторе Земли, заявили о суверенитете над геостационарными орбитами над своей территорией, но эти претензии не получили международного признания. [53]
Предложение штата
Статит — гипотетический спутник, который использует давление солнечного излучения на солнечный парус для изменения своей орбиты.
Он будет удерживать свое местоположение над темной стороной Земли на широте около 30 градусов. Статит неподвижен относительно системы Земли и Солнца, а не относительно поверхности Земли, и может ослабить перегрузку в геостационарном кольце. [54] [55]
Отставные спутники
Геостационарным спутникам требуется некоторое удержание на станции , чтобы сохранять свое положение, и как только у них заканчивается топливо для двигателей, их обычно снимают с эксплуатации. Транспондеры и другие бортовые системы часто переживают топливо для двигателей, и, позволяя спутнику естественным образом перейти на наклонную геосинхронную орбиту, некоторые спутники могут оставаться в эксплуатации, [56] или же быть поднятыми на орбиту захоронения . Этот процесс становится все более регулируемым, и спутники должны иметь 90%-ную вероятность перемещения более чем на 200 км выше геостационарного пояса в конце срока службы. [57]
Космический мусор

Космический мусор на геостационарных орбитах обычно имеет более низкую скорость столкновения, чем на низкой околоземной орбите (НОО), поскольку все спутники ГСО вращаются в одной плоскости, на одной высоте и с одинаковой скоростью; однако наличие спутников на эксцентрических орбитах допускает столкновения на скорости до 4 км/с. Хотя столкновение сравнительно маловероятно, спутники ГСО имеют ограниченную возможность избегать любого мусора. [58]
На геосинхронной высоте объекты диаметром менее 10 см не видны с Земли, что затрудняет оценку их распространенности. [59]
Несмотря на усилия по снижению риска, столкновения космических аппаратов происходили. Телекоммуникационный спутник Европейского космического агентства Olympus-1 был поражен метеоритом 11 августа 1993 года и в конечном итоге перешел на орбиту захоронения , [60] а в 2006 году российский спутник связи Express-AM11 был поражен неизвестным объектом и вышел из строя, [61] хотя у его инженеров было достаточно времени контакта со спутником, чтобы отправить его на орбиту захоронения. В 2017 году и AMC-9 , и Telkom-1 развалились по неизвестной причине. [62] [59] [63]
Характеристики
Типичная геостационарная орбита имеет следующие свойства:
- Наклон: 0°
- Период: 1436 минут (одни звездные сутки ) [23] : 121
- Эксцентриситет: 0
- Аргумент перигея: не определен
- Большая полуось : 42 164 км
Наклон
Нулевой наклон гарантирует, что орбита все время остается над экватором, делая ее неподвижной по отношению к широте с точки зрения наземного наблюдателя (и в геоцентрической системе отсчета, фиксированной вокруг Земли). [23] : 122
Период
Орбитальный период равен ровно одному сидерическому дню. Это означает, что спутник будет возвращаться в ту же точку над поверхностью Земли каждые (сидерические) сутки, независимо от других орбитальных свойств. Для геостационарной орбиты в частности, это гарантирует, что она будет удерживать ту же долготу с течением времени. [23] : 121 Этот орбитальный период, T , напрямую связан с большой полуосью орбиты через формулу:
где:
- а — длина большой полуоси орбиты
- μ — стандартный гравитационный параметр центрального тела [23] : 137
Эксцентриситет
Эксцентриситет равен нулю, что создает круговую орбиту . Это гарантирует, что спутник не будет приближаться или удаляться от Земли, что заставило бы его двигаться вперед и назад по небу. [ 23] : 122
Стабильность
Геостационарная орбита может быть достигнута только на высоте, очень близкой к 35 786 километрам (22 236 миль) и прямо над экватором. Это соответствует орбитальной скорости 3,07 километра в секунду (1,91 мили в секунду) и орбитальному периоду 1436 минут, один звездный день . Это гарантирует, что спутник будет соответствовать периоду вращения Земли и будет иметь стационарный след на земле. Все геостационарные спутники должны быть расположены на этом кольце.
Сочетание лунной гравитации, солнечной гравитации и сплющивания Земли на полюсах вызывает прецессионное движение плоскости орбиты любого геостационарного объекта с орбитальным периодом около 53 лет и начальным градиентом наклона около 0,85° в год, достигая максимального наклона 15° через 26,5 лет. [64] [23] : 156 Для исправления этого возмущения необходимы регулярные маневры по поддержанию орбитальной станции , составляющие дельта-v около 50 м/с в год. [65]
Вторым эффектом, который следует учитывать, является продольный дрейф, вызванный асимметрией Земли – экватор слегка эллиптичен ( экваториальный эксцентриситет ). [23] : 156 Существуют две устойчивые точки равновесия, иногда называемые «гравитационными колодцами» [66] (на 75,3° в. д. и 108° з. д.) и две соответствующие неустойчивые точки (на 165,3° в. д. и 14,7° з. д.). Любой геостационарный объект, помещенный между точками равновесия, будет (без какого-либо воздействия) медленно ускоряться в направлении устойчивого положения равновесия, вызывая периодическое изменение долготы. [64] Исправление этого эффекта требует маневров удержания станции с максимальной дельта-v около 2 м/с в год, в зависимости от желаемой долготы. [65]
Солнечный ветер и радиационное давление также оказывают небольшое воздействие на спутники: со временем они медленно отдаляются от своих предписанных орбит. [67]
При отсутствии миссий обслуживания с Земли или возобновляемого метода движения, потребление топлива двигателя для поддержания станции накладывает ограничение на срок службы спутника. Двигатели Холла , которые в настоящее время используются, имеют потенциал для продления срока службы спутника, обеспечивая высокоэффективную электрическую тягу . [65]
Вывод
Для круговых орбит вокруг тела центростремительная сила, необходимая для поддержания орбиты ( F c ), равна гравитационной силе, действующей на спутник ( F g ): [68]
Из закона всемирного тяготения Исаака Ньютона ,
- ,
где F g — гравитационная сила, действующая между двумя объектами, ME — масса Земли,5,9736 × 10 24 кг , м с - масса спутника, r - расстояние между центрами их масс , а G - гравитационная постоянная ,(6,674 28 ± 0,000 67 ) × 10 −11 м 3 кг −1 с −2 . [68]
Величина ускорения a тела, движущегося по окружности, определяется по формуле:
где v — величина скорости ( т.е. скорость) спутника. Из второго закона движения Ньютона центростремительная сила F c определяется по формуле:
- . [68]
Так как Fc = Fg ,
- ,
так что
Заменив v на уравнение скорости объекта, движущегося по окружности, получим:
где T — орбитальный период (т.е. одни звездные сутки), и он равен86 164 .090 54 с . [69] Это дает уравнение для r : [70]
Произведение GM E известно с гораздо большей точностью, чем любой из факторов по отдельности; оно известно как геоцентрическая гравитационная постоянная μ =398 600 .4418 ± 0.0008 км 3 с −2 . Следовательно
Полученный радиус орбиты составляет 42 164 километра (26 199 миль). Вычитая экваториальный радиус Земли , 6 378 километров (3 963 мили), получаем высоту 35 786 километров (22 236 миль). [71]
Орбитальная скорость рассчитывается путем умножения угловой скорости на радиус орбиты:
На других планетах
Тем же методом можно определить высоту орбиты для любой подобной пары тел, включая ареостационарную орбиту объекта относительно Марса , если предположить, что он сферический (что не совсем так). [72] Гравитационная постоянная GM ( μ ) для Марса имеет значение42 830 км 3 с −2 , его экваториальный радиус составляет3 389 , 50 км , а известный период вращения ( T ) планеты равен1,025 956 76 земных дней (88 642 .66 с ). Используя эти значения, высота орбиты Марса равна17 039 км . [73]
Смотрите также
- Список орбит
- Список спутников на геосинхронной орбите
- Орбитальное стационарное удержание
- Космический лифт , который в конечном итоге достигает геостационарной орбиты и выходит за ее пределы
Пояснительные записки
- ^ Геостационарная орбита и геосинхронная (экваториальная) орбита в источниках используются как взаимозаменяемые.
- ^ Орбитальные периоды и скорости рассчитываются с использованием соотношений 4π 2 R 3 = T 2 GM и V 2 R = GM , где R — радиус орбиты в метрах; T — орбитальный период в секундах; V — орбитальная скорость в м/с; G — гравитационная постоянная ≈6,673 × 10−11 Нм 2 /кг 2 ; M , масса Земли ≈5,98 × 10 24 кг .
- ^ Орбита Луны не идеально круговая и находится примерно в 8,6 раза дальше от Земли, чем геостационарное кольцо, когда Луна находится в перигее (363 104 км ÷ 42 164 км), и в 9,6 раза дальше, когда Луна находится в апогее (405 696 км ÷ 42 164 км).
Ссылки
- ^ Нордунг, Герман (1929). Das Issue der Befahrung des Weltraums: Der Raketen-Motor (PDF) . Берлин: Ричард Карл Шмидт и компания, стр. 98–100 .
- ^ "(Сообщение Корвуса отправлено) в небольшое, приземистое здание на окраине Норт-Лэндинга. Его швырнули в небо. ... Оно ... прибыло на ретрансляционную станцию усталым и изношенным, ... когда оно достигло космической станции всего в пятистах милях над городом Норт-Лэндинг". Смит, Джордж О. (1976). Полная Венера Равносторонняя. Нью-Йорк: Ballantine Books . стр. 3– 4. ISBN 978-0-345-28953-7.
- ^ "Поэтому вполне возможно, что эти истории повлияли на меня подсознательно, когда ... я разрабатывал принципы синхронных спутников связи ...", МакАлир, Нил (1992). Артур К. Кларк. Contemporary Books. стр. 54. ISBN 978-0-809-24324-2.
- ^ ab Артур К. Кларк (октябрь 1945 г.). «Внеземные ретрансляторы: могут ли ракетные станции обеспечить всемирное радиопокрытие?» (PDF) . Институт космического образования Артура К. Кларка. Архивировано (PDF) из оригинала 9 октября 2022 г. . Получено 1 января 2021 г. .
- ^ Филлипс Дэвис (ред.). «Основы космического полета. Раздел 1. Часть 5. Геостационарные орбиты». NASA . Архивировано из оригинала 12 декабря 2012 г. Получено 25 августа 2019 г.
- ↑ Миллс, Майк (3 августа 1997 г.). «Войны орбит: Артур Кларк и глобальный спутник связи». The Washington Post Magazine . стр. 12–13 . Получено 25 августа 2019 г.
- ^ Kidder, SQ (2015). «Спутники и спутниковое дистанционное зондирование: Орбиты». В North, Gerald; Pyla, John; Zhang, Fuqing (ред.). Encyclopedia of Atmospheric Sciences (2-е изд.). Elsiver. стр. 95–106 . doi :10.1016/B978-0-12-382225-3.00362-5. ISBN 9780123822253.
- ^ abcd МакКлинток, Джек (9 ноября 2003 г.). «Связь: Гарольд Розен – провидец геостационарных спутников». Журнал Discover . Получено 25 августа 2019 г.
- ↑ Перкинс, Роберт (31 января 2017 г.). Гарольд Розен, 1926–2017. Калтех . Получено 25 августа 2019 г.
- ^ abcd Вартабедян, Ральф (26 июля 2013 г.). «Как спутник под названием Syncom изменил мир». Los Angeles Times . Получено 25 августа 2019 г.
- ^ Дэниел Р. Гловер (1997). "Глава 6: Экспериментальные спутники связи НАСА, 1958-1995". В Andrew J Butrica (ред.). Beyond The Ionosphere: Fifty Years of Satellite Communication . NASA. Bibcode :1997bify.book.....B.
- ^ Дэвид Р. Уильямс (ред.). «Синком 2». НАСА . Проверено 29 сентября 2019 г.
- ^ "World's First Geosynchronous Satellite Launched". History Channel . Foxtel. 19 июня 2016 г. Архивировано из оригинала 7 декабря 2019 г. Получено 25 августа 2019 г.
- ^ Дэвид Р. Уильямс (ред.). «Синком 3». НАСА . Проверено 29 сентября 2019 г.
- ^ Хауэлл, Элизабет (24 апреля 2015 г.). «Что такое геосинхронная орбита?». Space.com . Получено 25 августа 2019 г.
- ^ "МСЭ выпускает глобальные и региональные оценки ИКТ за 2018 год". Международный союз электросвязи . 7 декабря 2018 г. Получено 25 августа 2019 г.
- ^ Томпсон, Джефф (24 апреля 2019 г.). «Австралии обещали сверхбыстрый широкополосный доступ с NBN. Вот что мы получили». ABC . Получено 25 августа 2019 г.
- ^ Тибкен, Шара (22 октября 2018 г.). «В сельской местности забудьте о широкополосном доступе. У вас может вообще не быть интернета. 5G уже не за горами, но некоторые районы Америки все еще не могут получить базовый доступ в интернет». CNET . Получено 25 августа 2019 г.
- ^ "Орбиты". ESA . 4 октября 2018 г. . Получено 1 октября 2019 г. .
- ^ ab "Развертывание демонстрации системы SBAS в Южной Африке". GMV . 6 августа 2016 г. Получено 1 октября 2019 г.
- ^ Ричард Томпсон. «Спутники, геостационарные орбиты и солнечные затмения». BOM . Получено 1 октября 2019 г.
- ^ ab Soler, Tomás; Eisemann, David W. (август 1994 г.). "Определение углов обзора геостационарных спутников связи" (PDF) . Journal of Surveying Engineering . 120 (3): 123. doi :10.1061/(ASCE)0733-9453(1994)120:3(115). ISSN 0733-9453. Архивировано (PDF) из оригинала 9 октября 2022 г. . Получено 16 апреля 2019 г. .
- ^ abcdefghi Wertz, James Richard; Larson, Wiley J. (1999). Larson, Wiley J.; Wertz, James R. (ред.). Анализ и проектирование космических миссий . Microcosm Press и Kluwer Academic Publishers. Bibcode : 1999smad.book.....W. ISBN 1-881883-10-8.
- ^ Кон, Дэниел (6 марта 2016 г.). «Сеть Teledesic: использование спутников на низкой околоземной орбите для предоставления широкополосного беспроводного доступа в Интернет в реальном времени по всему миру». Teledesic Corporation, США.
- ^ Freeman, Roger L. (22 июля 2002 г.). "Спутниковая связь". Справочное руководство по телекоммуникационной технике . Американское онкологическое общество. doi :10.1002/0471208051.fre018. ISBN 0471208051.
- ↑ Исторический комитет Американского астронавтического общества (23 августа 2010 г.). Джонсон, Стивен Б. (ред.). Исследование космоса и человечество: историческая энциклопедия. Том 1. Greenwood Publishing Group. стр. 416. ISBN 978-1-85109-514-8. Получено 17 апреля 2019 г. .
- ^ "Satellite Status". Всемирная метеорологическая организация . Получено 6 июля 2019 г.
- ^ "Наши спутники". Национальная служба спутниковых данных и информации об окружающей среде NOAA (NESDIS) .
- ^ "Meteosat". EUMETSAT.int . Архивировано из оригинала 14 января 2020 г. . Получено 1 июля 2019 г. .
- ^ "Satellite Launches for the Middle East and South Korea" (PDF) . Arianespace. Архивировано из оригинала (PDF) 4 июля 2010 г. . Получено 26 июня 2010 г. .
- ↑ Heinrich, Ralph (9 сентября 2014 г.). «Airbus Defence and Space поддерживает южнокорейскую программу метеорологических спутников». Airbus . Архивировано из оригинала 26 декабря 2019 г. Получено 2 июля 2019 г.
- ^ Грэм, Уильям (6 октября 2014 г.). «Япония запускает метеорологический спутник Химавари-8 с помощью ракеты H-IIA» . NASASpaceFlight.com.
- ^ "Китай планирует запустить еще девять метеорологических спутников Fengyun к 2025 году". GBTimes . 15 ноября 2018 г. Архивировано из оригинала 2 июля 2019 г. Получено 2 июля 2019 г.
- ^ ab "RAPID: Gateway to Indian Weather Satellite Data". Indian Space Research Organisation. 2 июля 2019 г. Архивировано из оригинала 25 декабря 2019 г. Получено 2 июля 2019 г.
- ^ ab "О спутниках окружающей среды". BOM . Получено 6 июля 2019 г. .
- ^ «Покрытие геостационарного спутника Земли». Планетарное общество.
- ^ "Спутники NOAA, ученые отслеживают возможное извержение вулкана Сент-Хеленс". SpaceRef . 6 октября 2004 г. Архивировано из оригинала 10 сентября 2012 г. Получено 1 июля 2019 г.
- ^ "GOCI". NASA. Архивировано из оригинала 24 июня 2021 г. Получено 25 августа 2019 г.
- ^ Миура, Томоаки; Нагай, Шин; Такеучи, Мика; Ичии, Кадзухито; Ёсиока, Хироки (30 октября 2019 г.). «Улучшенная характеристика сезонной динамики растительности и поверхности суши в Центральной Японии с помощью гипервременных данных Химавари-8». Научные отчеты . 9 (1): 15692. Бибкод : 2019НатСР...915692М. дои : 10.1038/s41598-019-52076-x. ISSN 2045-2322. ПМЦ 6821777 . ПМИД 31666582.
- ^ ab Hanson, Derek; Peronto, James; Hilderbrand, Douglas (12 ноября 2015 г.). «NOAA's Eyes in the Sky – After Five Decades of Weather Forecasting with Environmental Satellites, What Do Future Satellites Promise for Meteorologists and Society?» (Глаза NOAA в небе – что обещают метеорологам и обществу будущие спутники после пяти десятилетий прогнозирования погоды с помощью экологических спутников?). Всемирная метеорологическая организация . Архивировано из оригинала 18 декабря 2023 г. . Получено 2 июля 2019 г.
- ^ "GOES-R: сегодняшний спутник для завтрашнего прогнозного набора данных". Наука на сфере . NOAA . 14 ноября 2016 г.
- ^ Толлефсон, Джефф (2 марта 2018 г.). «Последние данные с американского метеорологического спутника освещают проблемы прогнозирования». Nature . 555 (7695): 154. Bibcode :2018Natur.555..154T. doi : 10.1038/d41586-018-02630-w . PMID 29517031.
- ^ «Спутниковая навигация – WAAS – Как это работает». FAA . 12 июня 2019 г.
- ^ "Проект испытательного стенда спутниковой системы дополнения". Geoscience Australia. Архивировано из оригинала 7 июля 2019 г.
- ^ "Система GAGAN сертифицирована для операций RNP0.1" (пресс-релиз). Индийская организация космических исследований . 3 января 2014 г. Архивировано из оригинала 3 января 2014 г.
- ^ Радхакришнан, С. Анил (11 января 2014 г.). «Система GAGAN готова к работе». The Hindu .
- ^ Отт, Л. Э. Матток, К. (ред.). Десять лет опыта работы с коммерческой спутниковой навигационной системой . Международное сотрудничество в области спутниковой связи, Труды семинара AIAA/ESA. ESTEC, Нордвейк, Нидерланды. стр. 101. Bibcode : 1995ESASP.372..101O.
- ^ ab Farber, Nicholas; Aresini, Andrea; Wauthier, Pascal; Francken, Philippe (сентябрь 2007 г.). Общий подход к восстановлению миссии на геостационарной переходной орбите. 20-й Международный симпозиум по динамике космического полета. стр. 2.
- ^ "Запуск спутников". Eumetsat . Архивировано из оригинала 21 декабря 2019 г. Получено 22 июля 2019 г.
- ^ Джейсон Дэвис (17 января 2014 г.). «Как вывести спутник на геостационарную орбиту». Планетарное общество . Получено 2 октября 2019 г.
- ^ Анри, Ивон. "Механизм регистрации процедур распределения орбиты/спектра в соответствии с Регламентом радиосвязи". Департамент космических служб. Архивировано из оригинала 27 марта 2009 г.
- ^ "Space Services Division". ITU . Получено 26 июля 2019 г. .
- ^ Одунтан, Гбенга. «Бесконечный спор: правовые теории о пространственной демаркационной плоскости границы между воздушным пространством и космическим пространством». Hertfordshire Law Journal . 1 (2): 75. S2CID 10047170.
- ^ Патент США 5183225, Форвард, Роберт, «СТАТИТ: КОСМИЧЕСКИЙ АППАРАТ, ИСПОЛЬЗУЮЩИЙ ДАВЛЕНИЕ В ВИДЕ И СПОСОБ ИСПОЛЬЗОВАНИЯ», опубликован 2 февраля 1993 г.
- ^ "Наука: Полярный "спутник" может произвести революцию в области связи". New Scientist . № 1759. 9 марта 1991 г. Получено 2 октября 2019 г.
- ^ "Работа на наклонной орбите". SatSig.net .
- ^ EUMETSAT (3 апреля 2017 г.). «Где умирают старые спутники». phys.org .
- ^ Маррик Стивенс (12 декабря 2017 г.). «Угроза космического мусора для геостационарных спутников была существенно недооценена». Physics World .
- ^ ab Caleb Henry (30 августа 2017 г.). «Видео ExoAnalytic показывает, как спутник Telkom-1 извергает обломки». SpaceNews.com .
- ↑ Пресс-релиз ESA «Провал Olympus» , 26 августа 1993 г. Архивировано 11 сентября 2007 г. на Wayback Machine.
- ↑ «Уведомление пользователей спутника «Экспресс-АМ11» в связи с аварией космического аппарата» ФГУП «Космическая связь» , 19 апреля 2006 г.
- ^ Данстан, Джеймс Э. (30 января 2018 г.). «Заботимся ли мы об орбитальном мусоре вообще?». SpaceNews.com .
- ^ «Аномалия спутника AMC 9, связанная с энергетическим событием и внезапным изменением орбиты – Spaceflight101». spaceflight101.com . 20 июня 2017 г.
- ^ ab Anderson, Paul; et al. (2015). Operational Considerations of GEO Debris Synchronization Dynamics (PDF) . 66-й Международный астронавтический конгресс . Иерусалим, Израиль. IAC-15,A6,7,3,x27478. Архивировано (PDF) из оригинала 9 октября 2022 г.
- ^ abc Дандек, М.; Довейл, Ф.; Арсис, Н.; Зурбах, С. (2012). Плазменный двигатель для геостационарных спутников для телекоммуникационных и межпланетных миссий . Серия конференций IOP: Материаловедение и инженерия. doi : 10.1088/1757-899X/29/1/012010 .
- ^ Джефферсон Баркер (март 2006 г.). Справочный текст по военному космосу США (PDF) . Институт национальной безопасности космоса. стр. 56.
- ^ Келли, Патрик; Эрвин, Ричард С.; Бевилаква, Риккардо; Мазал, Леонель (2016). Приложения давления солнечного излучения на геостационарных спутниках (PDF) . Труды конференции AAS GP & C 2016 года. Американское астронавтическое общество . Архивировано (PDF) из оригинала 9 октября 2022 г.
- ^ abc Попл, Стивен (2001). Продвинутая физика через диаграммы. Oxford University Press. стр. 72. ISBN 0-19-914199-1.
- ↑ Под редакцией П. Кеннета Зайдельмана, «Пояснительное приложение к астрономическому альманаху», University Science Books, 1992, стр. 700.
- ^ Mohindroo, KK (1997). Основные принципы физики. Том 1. Нью-Дели: Pitambar Publishing Company. С. 6–8.19. ISBN 81-209-0199-1.
- ^ Элерт, Гленн (2019). «Орбитальная механика I». The Physics Hypertextbook . Получено 30 сентября 2019 г.
- ^ Lakdawalla, Emily (2013). "Stationkeeping in Mars orbit". Планетарное общество . Получено 30 сентября 2019 г.
- ^ "Solar System Dynamics". NASA. 2017. Получено 30 сентября 2019 .
![]() В этой статье использованы материалы из общедоступного Федерального стандарта 1037C. Администрация общих служб . Архивировано из оригинала 22 января 2022 г. (в поддержку MIL-STD-188 ).
В этой статье использованы материалы из общедоступного Федерального стандарта 1037C. Администрация общих служб . Архивировано из оригинала 22 января 2022 г. (в поддержку MIL-STD-188 ).
Внешние ссылки
- Как вывести спутник на геостационарную орбиту
- Орбитальная механика (ракетно-космическая техника)
- Список спутников на геостационарной орбите
- Калькулятор моментального снимка пояса Кларка
- 3D-слежение за спутниками в реальном времени
- Обзор геостационарной спутниковой орбиты
- Ежедневная анимация Земли, сделанная геостационарным спутником «Электро Л». Фотографии. Спутник делает 48 снимков планеты каждый день.
- Орбитальная механика для студентов-инженеров








![{\displaystyle r={\sqrt[{3}]{\frac {GM_{\text{E}}T^{2}}{4\pi ^{2}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f82a14e92ba3a8e9c78590fd4acbb436884d19a3)
![{\displaystyle r={\sqrt[{3}]{\frac {\mu T^{2}}{4\pi ^{2}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/43ba4d2a4b1f1550a6c499c350f76d0911ae4384)
