Призма (геометрия)

Набор однородных $n-$ угольных призм
Набор однородных n- угольных призм
	Пример: однородная шестиугольная призма ( n = 6 )
Тип	однородный в смысле полуправильного многогранника
Лица	2 n -сторонних правильных многоугольника ; n квадратов
Края	3 н
Вершины	2 н
Эйлеров символ.	2
Конфигурация вершины	4.4.н
Символ Шлефли	{ n }×{ } ; т{2, n }
нотация Конвея	П н
Диаграмма Коксетера
Группа симметрии	D n h , [ n ,2], (* n 22), порядок 4 n
Группа вращения	D n , [ n ,2] + , ( n 22), порядок 2 n
Двойной многогранник	выпуклая двойственно- однородная n -угольная бипирамида
Характеристики	выпуклый, правильные многоугольные грани, изогональный , смещенные основания, стороны ⊥ оснований
Сеть
	Пример: развертка однородной девятиугольной призмы ( n = 9 )

Тело с 2 параллельными n-угольными основаниями, соединенными n параллелограммами

В геометрии призма — это многогранник , состоящий из $n-$ стороннего многоугольного основания , второго основания, которое является перенесенной копией (жестко перемещенной без вращения) первого, и $n$ других граней , обязательно все параллелограммы , соединяющие соответствующие стороны двух оснований. Все поперечные сечения, параллельные основаниям, являются переносами оснований. Призмы называются по их основаниям, например, призма с пятиугольным основанием называется пятиугольной призмой. Призмы являются подклассом призматоидов . ^[2]

Как и многие основные геометрические термины, слово призма (от греч. πρίσμα (prisma) «что-то распиленное») впервые было использовано в «Началах» Евклида . Евклид определил этот термин в Книге XI как «объемную фигуру, заключенную в две противоположные, равные и параллельные плоскости, в то время как остальные плоскости являются параллелограммами». Однако это определение подверглось критике за то, что оно было недостаточно конкретным в отношении природы оснований (причина некоторой путаницы среди поколений более поздних авторов геометрии). ^[3]^[4]

Наклонный против правого

Наклонная призма — это призма, в которой соединяющиеся ребра и грани не перпендикулярны граням основания.

Пример: параллелепипед — это наклонная призма, основанием которой является параллелограмм , или, что эквивалентно, многогранник с шестью гранями-параллелограммами.

Прямая призма — это призма , в которой соединяющиеся ребра и грани перпендикулярны базовым граням. ^[5] Это применимо тогда и только тогда, когда все соединяющиеся грани являются прямоугольными .

Двойственной прямой n - $призме$ является прямая $n$ - бипирамида .

Прямая призма (с прямоугольными сторонами) с правильными $n$ -угольными основаниями имеет символ Шлефли ${ }\times{n}.$ Она приближается к цилиндру , когда $n$ стремится к бесконечности . ^[6]

Особые случаи

Прямая прямоугольная призма (с прямоугольным основанием) также называется кубоидом или неформально прямоугольным ящиком . Прямая прямоугольная призма имеет символ Шлефли ${ }\times{ }\times{ }.$
Прямая квадратная призма (с квадратным основанием) также называется квадратным кубоидом или неформально квадратным ящиком .

Примечание: в некоторых текстах термин «прямоугольная призма» или «квадратная призма» может применяться как к прямой призме с прямоугольным основанием, так и к прямой призме с квадратным основанием.

Типы

Правильная призма

Правильная призма — это призма с правильными основаниями.

Равномерная призма

Однородная призма или полуправильная призма — это прямая призма с правильными основаниями и всеми ребрами одинаковой длины.

Таким образом, все боковые грани однородной призмы — квадраты .

Таким образом, все грани однородной призмы являются правильными многоугольниками. Кроме того, такие призмы являются изогональными ; таким образом, они являются однородными многогранниками . Они образуют одну из двух бесконечных серий полуправильных многогранников , другая серия образована антипризмами .

Однородная $n$ -угольная призма имеет символ Шлефли $t{2, n}.$

Семейство однородных n- угольных призм в т е
Имя призмы	Дигональная призма	(Треугольная) Треугольная призма	(Тетрагональная) Квадратная призма	Пятиугольная призма	Шестиугольная призма	Семиугольная призма	Восьмиугольная призма	Девятиугольная призма	Десятиугольная призма	Одиннадцатиугольная призма	Двенадцатиугольная призма	...	Апейрогональная призма
Изображение многогранника												...
Сферическое мозаичное изображение												Изображение мозаики плоскости
Конфигурация вершины.	2.4.4	3.4.4	4.4.4	5.4.4	6.4.4	7.4.4	8.4.4	9.4.4	10.4.4	11.4.4	12.4.4	...	∞.4.4
Диаграмма Коксетера												...

Характеристики

Объем

Объем призмы равен произведению площади основания на высоту, т.е. расстояние между двумя гранями основания (в случае неправильной призмы следует отметить, что это означает перпендикулярное расстояние).

Таким образом, объем составляет:

V=Bh,

где $B$ — площадь основания, а $h$ — высота.

Объем призмы, основанием которой является $n$ -сторонний правильный многоугольник с длиной стороны $s$ , равен: $V={\frac {n}{4}}hs^{2}\cot {\frac {\pi }{n}}.$

Площадь поверхности

Площадь поверхности прямой призмы равна:

2B+Ph,

где $B$ — площадь основания, $h$ — высота, а $P$ — периметр основания .

Площадь поверхности прямой призмы, основание которой представляет собой правильный $n$ - угольник с длиной стороны $s$ и высотой $h$ , равна:

A={\frac {n}{2}}s^{2}\cot {\frac {\pi }{n}}+nsh.

Симметрия

Группа симметрии прямой $n$ -гранной призмы с правильным основанием — $D n h$ порядка $4 n$ , за исключением случая куба, который имеет большую группу симметрии $O h$ порядка 48, которая имеет три версии $D 4h$ в качестве подгрупп . Группа вращения — $D n$ порядка $2 n$ , за исключением случая куба, который имеет большую группу симметрии $O$ порядка 24, которая имеет три версии $D 4$ в качестве подгрупп.

Группа симметрии $D n h$ содержит инверсию тогда и только тогда, когда $n$ четно.

Осоэдры и диэдры также обладают диэдральной симметрией, а $n$ -угольная призма может быть построена посредством геометрического усечения n $-$ угольного осоэдра, а также посредством кантелляции или расширения n $-$ угольного диэдра.

Диаграммы Шлегеля

П3	П4	П5	П6	П7	П8

Подобные многогранники

Усеченная призма

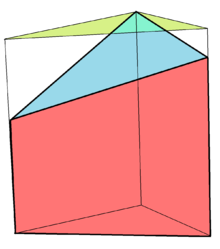
Пример усеченной треугольной призмы. Ее верхняя грань усечена под косым углом, но это не косая призма.

Усеченная призма образуется , когда призма разрезана плоскостью, которая не параллельна ее основаниям. Основания усеченной призмы не равны , а ее стороны не являются параллелограммами. ^[7]

Витая призма

Скрученная призма — это невыпуклый многогранник, построенный из однородной $n$ -призмы, каждая боковая грань которой разделена пополам по диагонали квадрата, путем скручивания вершины, обычно на ⁠ $π$ /н⁠ радианы ( ⁠180/н⁠ градусов) в том же направлении, в результате чего стороны становятся вогнутыми. ^[8]^[9]

Скрученную призму нельзя разбить на тетраэдры без добавления новых вершин. Простейшая скрученная призма имеет треугольные основания и называется многогранником Шёнхардта .

N $-$ угольная скрученная призма топологически идентична $n$ -угольной однородной антипризме , но имеет половину группы симметрии : $D n, [n,2] +$ , порядок $2 n$ . Ее можно рассматривать как невыпуклую антипризму с удаленными тетраэдрами между парами треугольников.

3-угольный	4-угольный		12-угольный
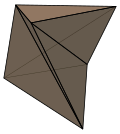многогранник Шёнхардта	Скрученная квадратная призма	Квадратная антипризма	Скрученная двенадцатиугольная антипризма

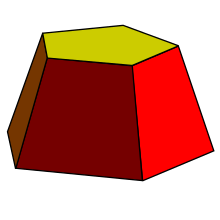
Усеченный конус

Усеченный конус — это конструкция, похожая на призму, с трапециевидными боковыми гранями и верхними и нижними многоугольниками разного размера.

Звездная призма

Звездчатая призма — это невыпуклый многогранник, образованный двумя одинаковыми гранями звездчатого многоугольника сверху и снизу, параллельными и смещенными на расстояние, и соединенными прямоугольными гранями. Однородная звездчатая призма будет иметь символ Шлефли ${p / q} \times { }$ с $p$ прямоугольниками и 2 ${p / q}$ гранями. Она топологически идентична $p$ -угольной призме.

Примеры
${ }\times{ } 180 \times{ }$	$т а {3}\times{ }$		${5/2}\times{ }$	${7/2}\times{ }$	${7/3}\times{ }$	${8/3}\times{ }$
$Д 2ч$ , заказ 8	$Д 3ч$ , заказ 12		$Д 5ч$ , заказ 20	$Д 7ч$ , заказ 28		$Д 8ч$ , заказ 32

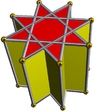Скрещенная призма

Скрещенная призма — это невыпуклый многогранник, построенный из призмы, в которой вершины одного основания перевернуты относительно центра этого основания (или повернуты на 180°). Это преобразует боковые прямоугольные грани в скрещенные прямоугольники . Для правильного многоугольного основания внешний вид представляет собой $n-$ угольные песочные часы . Все косые ребра проходят через один центр тела. Примечание: ни одна вершина не находится в этом центре тела. Скрещенная призма топологически идентична $n$ -угольной призме.

Примеры
${ }\times{ } 180 \times{ } 180$	$т а {3}\times{ } 180$		${3}\times{ } 180$	${4}\times{ } 180$	${5}\times{ } 180$	${5/2}\times{ } 180$	${6}\times{ } 180$
$Д 2ч$ , заказ 8	$D 3d$ , порядок 12			$Д 4ч$ , заказ 16	$Д 5д$ , заказ 20		$Д 6д$ , заказ 24

Тороидальная призма

Тороидальная призма — это невыпуклый многогранник, подобный скрещенной призме , но без нижних и верхних граней оснований и с простыми прямоугольными боковыми гранями, замыкающими многогранник. Это можно сделать только для четносторонних базовых многоугольников. Это топологические торы с эйлеровой характеристикой , равной нулю. Топологическая многогранная сетка может быть вырезана из двух рядов квадратной мозаики (с конфигурацией вершин $4.4.4.4$ ): полосы из $n$ квадратов, каждый из которых прикреплен к скрещенному прямоугольнику . $n$ -угольная тороидальная призма имеет $2 n$ вершин, $2 n$ граней: $n$ квадратов и $n$ скрещенных прямоугольников, и $4 n$ ребер. Она топологически самодвойственна .

Примеры
$Д 4ч$ , заказ 16	$Д 6ч$ , заказ 24
$В = 8$ , $Э = 16$ , $Ф = 8$	$В = 12$ , $Э = 24$ , $Ф = 12$

Призматический многогранник

Призматический многогранник — это обобщение призмы на более высокую размерность. $n-$ мерный призматический многогранник строится из двух ( $n$ $- 1 )-мерных многогранников, переведенных$ в следующее измерение.

Элементы призматического $n$ -ногогранника удваиваются из элементов ( $n - 1$ )-ногогранника, а затем создаются новые элементы из следующего нижнего элемента.

Возьмем $n$ -многогранник с $F i$ $i$ -элементами граней ( $i = 0, ..., n$ ). Его ( $n + 1$ )-многогранная призма будет иметь $2 F i + F i -1$ $i$ -элементов граней. (При $F -1 = 0$ , $F n = 1$ .)

По размеру:

Возьмем многоугольник с $n$ вершинами, $n$ ребрами. Его призма имеет $2 n$ вершин, $3 n$ ребр и $2 + n$ граней.
Возьмем многогранник с вершинами $V$ , ребрами $E$ и гранями $F.$ Его призма имеет $2 вершины V$ , $2 ребра E + V$ , $2 грани F + E$ и $2 + F$ ячеек.
Возьмем полихор с вершинами $V$ , ребрами $E$ , гранями $F$ и ячейками $C.$ Его призма имеет $2 вершины V$ , $2 ребра E + V$ , $2 грани F + E$ , $2 ячейки C + F$ и $2 + C$ гиперячейки.

Однородный призматический многогранник

Правильный $n$ -многогранник, представленный символом Шлефли ${p, q,..., t},$ может образовывать однородный призматический ( $n + 1$ )-многогранник, представленный декартовым произведением двух символов Шлефли : ${p, q,..., t}\times{ }.$

По размеру:

0-политопическая призма — это отрезок прямой , представленный пустым символом Шлефли ${ }.$
1-политопическая призма — это прямоугольник , образованный 2 сдвинутыми отрезками. Он представлен как произведение символов Шлефли ${ }\times{ }.$ Если это квадрат , симметрия может быть уменьшена: ${ }\times{ } = {4}.$
Пример:, Квадрат, ${ }\times{ },$ два параллельных отрезка прямой, соединенных двумя сторонами отрезка прямой .
Многоугольная призма — это трехмерная призма, образованная двумя сдвинутыми многоугольниками, соединенными прямоугольниками. Правильный многоугольник { $p} может$ построить равномерную $n$ -угольную призму, представленную произведением ${p}\times{ }.$ Если $p = 4$ , с симметрией квадратных сторон она становится кубом : ${4}\times{ } = {4,3}.$
Пример:, Пятиугольная призма , ${5}\times{ },$ два параллельных пятиугольника, соединенных 5 прямоугольными сторонами .
Многогранная призма — это 4-мерная призма, образованная из двух транслируемых многогранников , соединенных 3-мерными призматическими ячейками. Правильный многогранник ${p, q}$ может построить равномерную полихорическую призму, представленную произведением ${p, q}\times{ }.$ Если многогранник и стороны являются кубами, он становится тессерактом : { $4,3}\times{ } = {4,3,3}.$
Пример:, Додекаэдрическая призма , ${5,3}\times{ },$ два параллельных додекаэдра, соединенных 12 гранями пятиугольной призмы .
...

Призматические многогранники более высокого порядка также существуют как декартовы произведения любых двух или более многогранников. Размерность многогранника-произведения равна сумме размерностей его элементов. Первые примеры таких многогранников существуют в 4-мерном пространстве; они называются дуопризмами как произведение двух многоугольников в 4-мерном пространстве.

Правильные дуопризмы представлены как ${p}\times{q}$ с $pq$ вершинами, $2 pq$ ребрами, $pq$ квадратными гранями, $p$ $q$ -угольными гранями, $q$ $p$ -угольными гранями и ограничены $p$ $q$ -угольными призмами и $q$ $p$ -угольными призмами.

Например, ${4}\times{4},$ дуопризма 4-4 , является формой тессеракта с более низкой симметрией , как и ${4,3}\times{ },$ кубическая призма . ${4}\times{4}\times{ }$ (призма дуопризма 4-4), ${4,3}\times{4}$ (дуопризма куба-4) и ${4,3,3}\times{ }$ (тессерактическая призма) являются формами 5-куба с более низкой симметрией .

Смотрите также

Ссылки

^ Джонсон, Н. В. (2018). "Глава 11: Конечные группы симметрии". Геометрии и преобразования . Cambridge University Press. ISBN 978-1-107-10340-5.См. 11.3 Пирамиды, призмы и антипризмы, рисунок 11.3б.
^ Грюнбаум, Бранко (1997). «Изогональные призматоиды». Дискретная и вычислительная геометрия . 18 : 13–52 . doi : 10.1007/PL00009307 .
^ Малтон, Томас (1774). Королевская дорога в геометрию: или простое и знакомое введение в математику. автор, и продано. стр. 360.
^ Эллиот, Джеймс (1845). Ключ к полному трактату по практической геометрии и измерениям: содержащий полные демонстрации правил. Лонгман, Браун, Грин и Лонгманс. стр. 3.
^ Керн, Уильям Ф.; Блэнд, Джеймс Р. (1938). Solid Messuration с доказательствами . стр. 28.
^ Геретшлагер, Роберт (2020). Вовлечение молодых студентов в математику через соревнования: мировые перспективы и практики. Том 1. World Scientific . стр. 39. ISBN 978-981-120-582-8.
↑ Керн и Бланд (1938), стр. 81.
^ Горини, Кэтрин А. (2003). Факты в деле: Справочник по геометрии. стр. 172. ISBN 0-8160-4875-4.
^ «Фотографии скрученных призм».

Энтони Пью (1976). Многогранники: визуальный подход . Калифорния: Издательство Калифорнийского университета в Беркли. ISBN 0-520-03056-7.Глава 2: Архимедовы многогранники, призмы и антипризмы

Внешние ссылки

Вайсштейн, Эрик В. «Призма». MathWorld .
Бумажные модели призм и антипризм Бесплатные развертки призм и антипризм
Бумажные модели призм и антипризм с использованием сетей, созданных Stella

[1] Джонсон, Н. В. (2018). "Глава 11: Конечные группы симметрии". Геометрии и преобразования . Cambridge University Press. ISBN 978-1-107-10340-5.См. 11.3 Пирамиды, призмы и антипризмы, рисунок 11.3б.

[prismatoid-2] Грюнбаум, Бранко (1997). «Изогональные призматоиды». Дискретная и вычислительная геометрия . 18 : 13–52 . doi : 10.1007/PL00009307 .

[malton-1774-3] Малтон, Томас (1774). Королевская дорога в геометрию: или простое и знакомое введение в математику. автор, и продано. стр. 360.

[elliot-1845-4] Эллиот, Джеймс (1845). Ключ к полному трактату по практической геометрии и измерениям: содержащий полные демонстрации правил. Лонгман, Браун, Грин и Лонгманс. стр. 3.

[mensuration-5] Керн, Уильям Ф.; Блэнд, Джеймс Р. (1938). Solid Messuration с доказательствами . стр. 28.

[cylinder-6] Геретшлагер, Роберт (2020). Вовлечение молодых студентов в математику через соревнования: мировые перспективы и практики. Том 1. World Scientific . стр. 39. ISBN 978-981-120-582-8.

[FOOTNOTEKernBland193881-7] Керн и Бланд (1938), стр. 81.

[gorini-2003-8] Горини, Кэтрин А. (2003). Факты в деле: Справочник по геометрии. стр. 172. ISBN 0-8160-4875-4.

[9] «Фотографии скрученных призм».