Скин-эффект


В электромагнетизме скин-эффект — это тенденция переменного электрического тока (AC) распределяться внутри проводника таким образом, что плотность тока наибольшая вблизи поверхности проводника и уменьшается экспоненциально с увеличением глубины проводника. Он вызван встречными вихревыми токами, вызванными изменяющимся магнитным полем, возникающим в результате переменного тока. Электрический ток течет в основном по скин-слою проводника, между внешней поверхностью и уровнем, называемым глубиной скин-слоя .
Глубина скин-слоя зависит от частоты переменного тока; с увеличением частоты ток становится более сконцентрированным вблизи поверхности, что приводит к уменьшению глубины скин-слоя. Скин-эффект уменьшает эффективное сечение проводника и, таким образом, увеличивает его эффективное сопротивление . При 60 Гц в меди глубина скин-слоя составляет около 8,5 мм. На высоких частотах глубина скин-слоя становится намного меньше.
Повышенное сопротивление переменному току, вызванное скин-эффектом, можно смягчить, используя специализированный многожильный провод, называемый литцендрат . Поскольку внутренняя часть большого проводника проводит лишь небольшую часть тока, для экономии веса и стоимости можно использовать трубчатые проводники.
Скин-эффект имеет практические последствия при анализе и проектировании радиочастотных и микроволновых цепей, линий передачи (или волноводов) и антенн . Он также важен на частотах сети (50–60 Гц) в системах передачи и распределения электроэнергии переменного тока . Это одна из причин предпочтения постоянного тока высокого напряжения для передачи электроэнергии на большие расстояния.
Эффект был впервые описан в статье Горация Лэмба в 1883 году для случая сферических проводников [1] и был обобщен на проводники любой формы Оливером Хевисайдом в 1885 году.
Причина

Проводники, обычно в виде проводов, могут использоваться для передачи электрической энергии или сигналов с помощью переменного тока, протекающего через этот проводник. Носители заряда, составляющие этот ток, обычно электроны , приводятся в действие электрическим полем из-за источника электрической энергии. Ток в проводнике создает магнитное поле внутри и вокруг проводника. Когда интенсивность тока в проводнике изменяется, магнитное поле также изменяется. Изменение магнитного поля, в свою очередь, создает электрическое поле, которое противодействует изменению интенсивности тока. Это противодействующее электрическое поле называется противоэлектродвижущей силой (обратная ЭДС). Противоэлектродвижущая сила сильнее всего / наиболее сконцентрирована в центре проводника, пропуская ток только вблизи внешней оболочки проводника, как показано на схеме справа. [2] [3]
Независимо от движущей силы, плотность тока оказывается наибольшей на поверхности проводника, с уменьшением величины глубже в проводнике. Это снижение плотности тока известно как скин-эффект , а глубина скин-слоя является мерой глубины, на которой плотность тока падает до 1/e от ее значения вблизи поверхности. Более 98% тока будет протекать в слое, в 4 раза превышающем глубину скин-слоя от поверхности. Это поведение отличается от поведения постоянного тока , который обычно равномерно распределяется по поперечному сечению провода.
Переменный ток может также быть индуцирован в проводнике из-за переменного магнитного поля в соответствии с законом индукции . Электромагнитная волна, падающая на проводник, поэтому обычно производит такой ток; это объясняет затухание электромагнитных волн в металлах. Хотя термин скин-эффект чаще всего ассоциируется с приложениями, включающими передачу электрических токов, глубина скин-слоя также описывает экспоненциальное затухание электрических и магнитных полей, а также плотность индуцированных токов внутри объемного материала, когда плоская волна падает на него при нормальном падении .
Формула
Плотность переменного тока J в проводнике уменьшается экспоненциально от своего значения на поверхности J S в соответствии с глубиной d от поверхности следующим образом: [4] : 362 где называется глубиной скин-слоя , которая определяется как глубина под поверхностью проводника, на которой плотность тока падает до 1/ e (около 0,37) от J S . Мнимая часть экспоненты указывает на то, что фаза плотности тока задерживается на 1 радиан для каждой глубины проникновения скин-слоя. Одна полная длина волны в проводнике требует 2 π глубины скин-слоя, в этой точке плотность тока ослабевает до e −2 π (1,87×10 −3 , или −54,6 дБ) от ее поверхностного значения. Длина волны в проводнике намного короче длины волны в вакууме , или, что эквивалентно, фазовая скорость в проводнике намного медленнее скорости света в вакууме. Например, радиоволна частотой 1 МГц имеет длину волны в вакууме λ o около 300 м, тогда как в меди длина волны уменьшается всего до около 0,5 мм с фазовой скоростью всего около 500 м/с. Вследствие закона Снеллиуса и этой очень маленькой фазовой скорости в проводнике любая волна, входящая в проводник, даже при скользящем падении, преломляется в основном в направлении, перпендикулярном поверхности проводника.
Общая формула для определения глубины скин-слоя при отсутствии диэлектрических или магнитных потерь выглядит следующим образом: [5] [6]
где
- удельное сопротивление проводника
- Угловая частота тока , где - частота.
- проницаемость проводника,
- относительная магнитная проницаемость проводника
- проницаемость свободного пространства
- диэлектрическая проницаемость проводника,
- относительная диэлектрическая проницаемость проводника
- диэлектрическая проницаемость свободного пространства .
На частотах намного ниже величина внутри большого радикала близка к единице, и формулу чаще всего задают в виде:
Эта формула верна на частотах, далеких от сильных атомных или молекулярных резонансов (где будет большая мнимая часть), и на частотах, которые намного ниже как плазменной частоты материала (зависящей от плотности свободных электронов в материале), так и обратной величины среднего времени между столкновениями с участием электронов проводимости. В хороших проводниках, таких как металлы, все эти условия обеспечиваются по крайней мере до микроволновых частот, что подтверждает справедливость этой формулы. [примечание 1] Например, в случае меди это будет верно для частот намного ниже10 18 Гц .
Однако в очень плохих проводниках при достаточно высоких частотах множитель под большим радикалом увеличивается. При частотах, значительно превышающих можно показать, что глубина скин-слоя, вместо того чтобы продолжать уменьшаться, приближается к асимптотическому значению:
Это отклонение от обычной формулы применимо только к материалам с довольно низкой проводимостью и на частотах, где длина волны вакуума не намного больше самой глубины скин-слоя. Например, объемный кремний (нелегированный) является плохим проводником и имеет глубину скин-слоя около 40 метров на частоте 100 кГц ( λ = 3 км). Однако по мере увеличения частоты до мегагерцового диапазона его глубина скин-слоя никогда не опускается ниже асимптотического значения 11 метров. Вывод заключается в том, что в плохих сплошных проводниках, таких как нелегированный кремний, скин-эффект не нужно учитывать в большинстве практических ситуаций: любой ток равномерно распределен по всему поперечному сечению материала, независимо от его частоты.
Круглая проволока
Когда глубина скин-слоя не мала по отношению к радиусу провода, плотность тока может быть описана в терминах функций Бесселя . Плотность тока внутри круглого провода вдали от влияния других полей, как функция расстояния от оси, определяется по формуле: [7] : 38
где
- расстояние от оси провода
- радиус провода
- Вектор плотности тока на расстоянии r от оси провода
- вектор плотности тока на поверхности провода
- общий вектор тока
- Функция Бесселя первого рода, порядок 0
- Функция Бесселя первого рода, порядка 1
- волновое число в проводнике
- также называется глубиной скин-слоя.
- удельное сопротивление проводника
- относительная магнитная проницаемость проводника
Поскольку является комплексным, функции Бесселя также являются комплексными. Амплитуда и фаза плотности тока изменяются с глубиной.
Вывод
Объединение уравнения электромагнитной волны и закона Ома дает Решение этого уравнения для конечного тока в центре проводника, где - функция Бесселя первого рода и - постоянный фазор. Чтобы удовлетворить граничному условию для плотности тока на поверхности проводника, должно быть Таким образом,
Сопротивление
Сопротивление
Наиболее важным эффектом скин-эффекта на импеданс одного провода является увеличение сопротивления провода и последующие потери . Эффективное сопротивление из-за тока, ограниченного вблизи поверхности большого проводника (намного толще, чем δ ), можно решить, как если бы ток протекал равномерно через слой толщиной δ на основе удельного сопротивления постоянного тока этого материала. Эффективная площадь поперечного сечения приблизительно равна δ, умноженному на окружность проводника. Таким образом, длинный цилиндрический проводник, такой как провод, имеющий диаметр D, большой по сравнению с δ , имеет сопротивление, приблизительно равное сопротивлению полой трубки с толщиной стенки δ, по которой проходит постоянный ток. Сопротивление переменного тока провода длиной ℓ и удельным сопротивлением равно:
Окончательное приближение выше предполагает .
Удобная формула (приписываемая Ф. Э. Терману ) для диаметра D W провода круглого сечения, сопротивление которого увеличится на 10 % при частоте f, выглядит следующим образом: [8]
Эта формула для увеличения сопротивления переменного тока точна только для изолированного провода. Для близлежащих проводов, например, в кабеле или катушке, сопротивление переменного тока также зависит от эффекта близости , который может вызвать дополнительное увеличение сопротивления переменного тока. Внутреннее сопротивление на единицу длины сегмента круглого провода определяется по формуле: [7] : 40
Это сопротивление представляет собой комплексную величину, соответствующую сопротивлению (действительному) последовательно с реактивным сопротивлением (мнимым), обусловленным внутренней самоиндукцией провода , на единицу длины.
Индуктивность
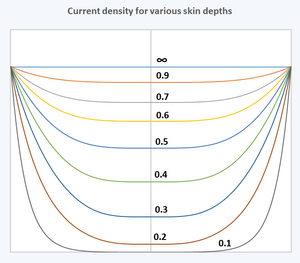
Часть индуктивности провода может быть отнесена к магнитному полю внутри самого провода, которое называется внутренней индуктивностью ; это учитывает индуктивное сопротивление (мнимая часть импеданса), заданное приведенной выше формулой. В большинстве случаев это небольшая часть индуктивности провода, которая включает в себя эффект индукции от магнитных полей снаружи провода, создаваемых током в проводе. В отличие от этой внешней индуктивности, внутренняя индуктивность уменьшается за счет скин-эффекта, то есть на частотах, где глубина скин-слоя больше не велика по сравнению с размером проводника. [9] Эта небольшая составляющая индуктивности приближается к значению (50 нГн/м для немагнитного провода) на низких частотах, независимо от радиуса провода. Ее уменьшение с ростом частоты, когда отношение глубины скин-слоя к радиусу провода падает ниже примерно 1, отображено на прилагаемом графике и объясняет уменьшение индуктивности телефонного кабеля с ростом частоты в таблице ниже.


Обратитесь к схеме ниже, показывающей внутренний и внешний проводники коаксиального кабеля. Поскольку скин-эффект заставляет ток на высоких частотах течь в основном по поверхности проводника, можно увидеть, что это уменьшит магнитное поле внутри провода, то есть ниже глубины, на которой течет основная часть тока. Можно показать, что это окажет незначительное влияние на самоиндукцию самого провода; см. Skilling [10] или Hayt [11] для математической обработки этого явления.
Индуктивность, рассматриваемая в этом контексте, относится к голому проводнику, а не к индуктивности катушки, используемой в качестве элемента цепи. Индуктивность катушки определяется взаимной индуктивностью между витками катушки, которая увеличивает ее индуктивность в соответствии с квадратом числа витков. Однако, когда задействован только один провод, то в дополнение к внешней индуктивности, включающей магнитные поля вне провода (из-за полного тока в проводе), как показано в белой области рисунка ниже, существует также гораздо меньшая составляющая внутренней индуктивности из-за части магнитного поля внутри самого провода, зеленая область на рисунке B. Эта небольшая составляющая индуктивности уменьшается, когда ток концентрируется по направлению к скин-слою проводника, то есть когда глубина скин-слоя не намного больше радиуса провода, как это будет иметь место на более высоких частотах.
Для одного провода это уменьшение становится все менее значимым по мере того, как провод становится длиннее по сравнению с его диаметром, и обычно им пренебрегают. Однако наличие второго проводника в случае линии передачи уменьшает величину внешнего магнитного поля (и общей самоиндукции) независимо от длины провода, так что уменьшение индуктивности из-за скин-эффекта все еще может быть важным. Например, в случае телефонной витой пары, ниже, индуктивность проводников существенно уменьшается на более высоких частотах, где скин-эффект становится важным. С другой стороны, когда внешняя составляющая индуктивности увеличивается из-за геометрии катушки (из-за взаимной индуктивности между витками), значимость внутренней составляющей индуктивности еще больше уменьшается и игнорируется.
Коаксиальный кабель
Пусть размеры a , b и c будут внутренним радиусом проводника, внутренним радиусом экрана (внешнего проводника) и внешним радиусом экрана соответственно, как показано на поперечном сечении рисунка A ниже.

Для заданного тока общая энергия, запасенная в магнитных полях, должна быть такой же, как расчетная электрическая энергия, приписываемая току, протекающему через индуктивность коаксиального кабеля; эта энергия пропорциональна измеренной индуктивности кабеля.
Магнитное поле внутри коаксиального кабеля можно разделить на три области, каждая из которых, следовательно, будет вносить вклад в электрическую индуктивность, наблюдаемую на участке кабеля. [12]
- Индуктивность связана с магнитным полем в области радиусом , области внутри центрального проводника.
- Индуктивность связана с магнитным полем в области между двумя проводниками (содержащими диэлектрик, возможно, воздух).
- Индуктивность связана с магнитным полем в области , области внутри экранированного проводника.
Чистая электрическая индуктивность обусловлена всеми тремя вкладами:
не изменяется под действием скин-эффекта и определяется часто цитируемой формулой для индуктивности L на единицу длины D коаксиального кабеля:
На низких частотах все три индуктивности присутствуют полностью, так что .
На высоких частотах магнитный поток имеется только в диэлектрической области, поэтому .
Большинство обсуждений коаксиальных линий передачи предполагают, что они будут использоваться для радиочастот, поэтому уравнения приведены только для последнего случая.
По мере увеличения скин-эффекта токи концентрируются вблизи внешней части внутреннего проводника ( r = a ) и внутренней части экрана ( r = b ). Поскольку по существу нет тока глубже во внутреннем проводнике, нет магнитного поля под поверхностью внутреннего проводника. Поскольку ток во внутреннем проводнике уравновешивается противоположным током, текущим внутри внешнего проводника, нет остаточного магнитного поля в самом внешнем проводнике, где . Вносит вклад только в электрическую индуктивность на этих более высоких частотах.
Несмотря на то, что геометрия отличается, витая пара, используемая в телефонных линиях, подвержена аналогичному воздействию: на более высоких частотах индуктивность уменьшается более чем на 20%, как видно из следующей таблицы.
Телефонный кабель
Репрезентативные данные параметров телефонного кабеля PIC 24 калибра при 21 °C (70 °F).
Частота
(Гц)R
(Ом/км)L
(мГн/км)G
(мкСм/км)С
(нФ/км)1 Гц 172.24 0,6129 0.000 51.57 1 кГц 172.28 0,6125 0,072 51.57 10 кГц 172.70 0,6099 0,531 51.57 100 кГц 191.63 0,5807 3.327 51.57 1 МГц 463,59 0,5062 29.111 51.57 2 МГц 643.14 0,4862 53.205 51.57 5 МГц 999.41 0,4675 118.074 51.57
Более подробные таблицы и таблицы для других датчиков, температур и типов доступны в Reeve. [13] Чен [14] приводит те же данные в параметризованной форме, которую, как он утверждает, можно использовать до 50 МГц.
Чен [14] приводит уравнение такого вида для телефонной витой пары:
Влияние материала на глубину скин-слоя
В хорошем проводнике глубина скин-слоя пропорциональна квадратному корню из удельного сопротивления. Это означает, что лучшие проводники имеют меньшую глубину скин-слоя. Общее сопротивление лучшего проводника остается ниже даже при меньшей глубине скин-слоя. Однако лучший проводник будет показывать более высокое соотношение между своим сопротивлением переменному и постоянному току по сравнению с проводником с большим удельным сопротивлением. Например, при 60 Гц медный проводник 2000 MCM (1000 квадратных миллиметров) имеет на 23% больше сопротивления, чем при постоянном токе. Проводник того же размера из алюминия имеет только на 10% больше сопротивления при переменном токе 60 Гц, чем при постоянном токе. [15]
Глубина скин-слоя также изменяется как обратный квадратный корень проницаемости проводника . В случае железа его проводимость составляет около 1/7 от проводимости меди. Однако, будучи ферромагнитным , его проницаемость примерно в 10 000 раз больше. Это уменьшает глубину скин-слоя для железа примерно до 1/38 от проводимости меди, около 220 микрометров при 60 Гц. Железный провод непрактичен для линий электропередач переменного тока (за исключением добавления механической прочности, выступая в качестве сердечника для неферромагнитного проводника, такого как алюминий). Скин-эффект также уменьшает эффективную толщину пластин в силовых трансформаторах, увеличивая их потери.
Железные прутки хорошо подходят для сварки постоянным током (DC) , но их трудно использовать на частотах, намного превышающих 60 Гц. На нескольких килогерцах железный сварочный пруток будет раскаляться докрасна, поскольку ток будет проходить через значительно возросшее сопротивление переменного тока, вызванное скин-эффектом, при этом для самой дуги останется относительно мало энергии . Для высокочастотной сварки используются только немагнитные прутки.
При частоте 1 мегагерц глубина скин-эффекта во влажной почве составляет около 5,0 м, в морской воде — около 0,25 м. [16]
Смягчение
Тип кабеля, называемый литцендрахт (от немецкого Litzendraht , плетеный провод), используется для смягчения скин-эффекта для частот от нескольких килогерц до примерно одного мегагерца. Он состоит из нескольких изолированных проволочных жил, сплетенных вместе в тщательно разработанном узоре, так что общее магнитное поле действует одинаково на все провода и заставляет общий ток распределяться равномерно между ними. Поскольку скин-эффект оказывает небольшое влияние на каждую из тонких жил, пучок не испытывает такого же увеличения сопротивления переменного тока, как сплошной проводник той же площади поперечного сечения из-за скин-эффекта. [17]
Литцендрат часто используется в обмотках высокочастотных трансформаторов для повышения их эффективности за счет смягчения как скин-эффекта, так и эффекта близости. Большие силовые трансформаторы наматываются многожильными проводниками, конструкция которых подобна конструкции литцендратного провода, но с большим поперечным сечением, соответствующим большей глубине скин-слоя на частотах сети. [18] Проводящие нити, состоящие из углеродных нанотрубок [19], были продемонстрированы в качестве проводников для антенн от средних волн до микроволновых частот. В отличие от стандартных проводников антенн, нанотрубки намного меньше глубины скин-слоя, что позволяет полностью использовать поперечное сечение нити, что приводит к чрезвычайно легкой антенне.
В высоковольтных сильноточных воздушных линиях электропередачи часто используется алюминиевый кабель со стальным армирующим сердечником ; более высокое сопротивление стального сердечника не имеет значения, поскольку он расположен намного ниже глубины скин-слоя, где по существу не протекает переменный ток.
В приложениях, где протекают высокие токи (до тысяч ампер), сплошные проводники обычно заменяются трубками, устраняя внутреннюю часть проводника, где протекает небольшой ток. Это почти не влияет на сопротивление переменного тока, но значительно снижает вес проводника. Высокая прочность, но малый вес трубок существенно увеличивает пропускную способность. Трубчатые проводники типичны для распределительных устройств электропитания, где расстояние между опорными изоляторами может составлять несколько метров. Длинные пролеты обычно демонстрируют физическое провисание, но это не влияет на электрические характеристики. Чтобы избежать потерь, проводимость материала трубки должна быть высокой.
В ситуациях с высоким током, когда проводники (круглая или плоская шина ) могут иметь толщину от 5 до 50 мм, скин-эффект также возникает на крутых изгибах, где металл сжимается внутри изгиба и растягивается снаружи изгиба. Более короткий путь на внутренней поверхности приводит к меньшему сопротивлению, что приводит к тому, что большая часть тока концентрируется вблизи внутренней поверхности изгиба. Это вызывает повышение температуры в этой области по сравнению с прямой (неизогнутой) областью того же проводника. Похожий скин-эффект возникает в углах прямоугольных проводников (при рассмотрении в поперечном сечении), где магнитное поле больше концентрируется в углах, чем в сторонах. Это приводит к превосходной производительности (т. е. более высокому току при меньшем повышении температуры) от широких тонких проводников (например, ленточных проводников), в которых эффекты от углов эффективно устранены.
Из этого следует, что трансформатор с круглым сердечником будет более эффективен, чем трансформатор эквивалентных номиналов с квадратным или прямоугольным сердечником из того же материала.
Сплошные или трубчатые проводники могут быть посеребрены , чтобы воспользоваться более высокой проводимостью серебра. Эта техника особенно используется на частотах от ОВЧ до СВЧ , где малая глубина скин-слоя требует только очень тонкого слоя серебра, что делает улучшение проводимости очень экономически эффективным. Серебряное покрытие аналогичным образом используется на поверхности волноводов, используемых для передачи микроволн. Это уменьшает затухание распространяющейся волны из-за резистивных потерь, влияющих на сопутствующие вихревые токи; скин-эффект ограничивает такие вихревые токи очень тонким поверхностным слоем структуры волновода. Сам по себе скин-эффект фактически не борется в этих случаях, но распределение токов вблизи поверхности проводника делает использование драгоценных металлов (имеющих более низкое удельное сопротивление) практичным. Хотя оно имеет более низкую проводимость, чем медь и серебро, золотое покрытие также используется, потому что в отличие от меди и серебра оно не подвергается коррозии. Тонкий окисленный слой меди или серебра будет иметь низкую проводимость и, следовательно, приведет к большим потерям мощности, поскольку большая часть тока все равно будет протекать через этот слой.
Недавно было показано, что метод наслаивания немагнитных и ферромагнитных материалов с толщиной в нанометровом масштабе смягчает повышенное сопротивление из-за скин-эффекта для очень высокочастотных приложений. [20] Рабочая теория заключается в том, что поведение ферромагнитных материалов на высоких частотах приводит к полям и/или токам, которые противостоят тем, которые генерируются относительно немагнитными материалами, но для проверки точных механизмов требуется больше работы. [ необходима цитата ] Как показали эксперименты, это может значительно повысить эффективность проводников, работающих на частотах десятков ГГц и выше. Это имеет серьезные последствия для связи 5G . [20]
Примеры
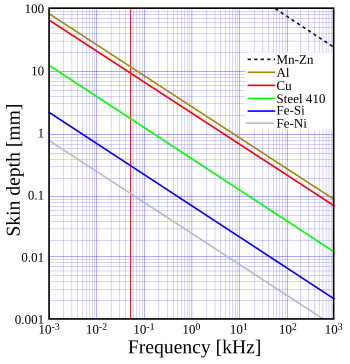
- Mn-Zn – магнитомягкий феррит
- Al – металлический алюминий
- Cu – металлическая медь
- сталь 410 – магнитная нержавеющая сталь
- Fe-Si – электротехническая сталь с ориентированной зернистостью
- Fe-Ni – пермалсой с высокой проницаемостью (80%Ni-20%Fe)
Мы можем вывести практическую формулу для определения глубины скин-слоя следующим образом:
где
- глубина скин-слоя в метрах
- затухание в
- проницаемость свободного пространства
- проницаемость среды
- проводимость среды (для меди, 58,5 × 10 6 См/м )
- частота тока в Гц
Золото является хорошим проводником с удельным сопротивлением2,44 × 10−8 Ом·м и по существу немагнитен: 1, поэтому его глубина скин-слоя на частоте 50 Гц определяется выражением
Свинец, напротив, является относительно плохим проводником (среди металлов) с удельным сопротивлением2,2 × 10 −7 Ω·м , что примерно в 9 раз больше, чем у золота. Его глубина скин-слоя при 50 Гц также составляет около 33 мм, или в разы больше, чем у золота.
Сильномагнитные материалы имеют уменьшенную глубину скин-слоя из-за их большой проницаемости , как было указано выше для случая железа, несмотря на его худшую проводимость. Практические последствия наблюдаются у пользователей индукционных плит , где некоторые типы посуды из нержавеющей стали непригодны для использования, поскольку они не являются ферромагнитными.
На очень высоких частотах глубина скин-слоя для хороших проводников становится крошечной. Например, глубина скин-слоя некоторых распространенных металлов на частоте 10 ГГц (микроволновая область) составляет менее микрометра :
Глубина скин-слоя на микроволновых частотах Дирижер Глубина скин-слоя
( мкм )Алюминий 0,820 Медь 0,652 Золото 0,753 Серебро 0,634
Таким образом, на микроволновых частотах большая часть тока протекает в чрезвычайно тонкой области вблизи поверхности. Поэтому омические потери волноводов на микроволновых частотах зависят только от поверхностного покрытия материала. Слой серебра толщиной 3 мкм , напыленный на кусок стекла, является, таким образом, отличным проводником на таких частотах.
В меди глубина скин-слоя уменьшается пропорционально квадратному корню частоты:
Глубина скин-слоя в меди Частота Глубина скин-слоя
(мкм)50 Гц 9220 60 Гц 8420 10 кГц 652 100 кГц 206 1 МГц 65.2 10 МГц 20.6 100 МГц 6.52 1 ГГц 2.06
В своей книге «Инженерная электромагнетика » Хейт указывает, что на электростанции шина для переменного тока частотой 60 Гц с радиусом больше одной трети дюйма (8 мм) является пустой тратой меди [21] , а на практике шины для сильного переменного тока редко имеют толщину более половины дюйма (12 мм), за исключением случаев, когда это обусловлено механическими причинами.
Электромагнитные волны
В электромагнитных волнах глубина скин-слоя — это глубина, на которой амплитуда электрического и магнитного полей уменьшилась на . [22] Интенсивность волны пропорциональна квадрату амплитуды, и, таким образом, глубина, на которой интенсивность уменьшилась на В волноводах потери из-за индуцированных токов происходят в основном в пределах одной глубины скин-слоя поверхности. Таким образом, покрытие поверхности волновода материалом с малой глубиной скин-слоя снижает потери. [23]
Аномальный скин-эффект
Для высоких частот и низких температур обычные формулы для глубины скин-слоя перестают работать. Этот эффект впервые заметил Хайнц Лондон в 1940 году, который правильно предположил, что он обусловлен средней длиной свободного пробега электронов, достигающих диапазона классической глубины скин-слоя. [24] Теория Маттиса-Бардина была разработана для этого конкретного случая для металлов и сверхпроводников .
Смотрите также
- Эффект близости (электромагнетизм)
- Вихревой ток
- Провод литцендрат
- Трансформатор
- Индукционная варка
- Индукционный нагрев
- Магнитное число Рейнольдса
- Правило инкрементной индуктивности Уиллера , метод оценки сопротивления скин-эффекта
Примечания
- ^ Обратите внимание, что приведенное выше уравнение для плотности тока внутри проводника как функции глубины применимо к случаям, когда обычное приближение для глубины скин-слоя выполняется. В крайних случаях, когда это не так, экспоненциальное уменьшение относительно глубины скин-слоя все еще применимо к величине индуцированных токов, однако мнимая часть показателя в этом уравнении, а следовательно, и фазовая скорость внутри материала, изменяются относительно этого уравнения.
Ссылки
- ↑ Лэмб, Гораций (1883-01-01). "XIII. Об электрических движениях в сферическом проводнике". Philosophical Transactions of the Royal Society of London . 174 : 519–549. doi :10.1098/rstl.1883.0013. S2CID 111283238.
- ^ Финк, Дональд Г.; Бити, Х. Уэйн (2000). Стандартный справочник для инженеров-электриков (14-е изд.). McGraw-Hill. стр. 2–50. ISBN 978-0-07-022005-8.
Эти ЭДС больше в центре, чем на окружности, поэтому разность потенциалов стремится установить токи, которые противодействуют току в центре и способствуют ему на окружности.
- ^ Джонсон, Ховард; Грэм, Мартин (2003). Высокоскоростное распространение сигнала. Расширенная черная магия (3-е изд.). Prentice Hall. С. 58–78. ISBN 978-0-13-084408-8Чтобы
понять скин-эффект, нужно сначала понять, как действуют вихревые токи...
- ^ Хейт, Уильям Х. (1989), Инженерная электромагнетика (5-е изд.), McGraw-Hill, ISBN 978-0070274068
- ^ Вандер Ворст, Розен и Коцука (2006)
- ^ Приведенная формула алгебраически эквивалентна формуле, найденной на странице 130 Джордана (1968, стр. 130)
- ^ ab Weeks, Walter L. (1981), Передача и распределение электроэнергии , Harper & Row, ISBN 978-0060469825
- ^ Терман 1943, стр. ??
- ^ Хайт (1981, стр. 303)
- ↑ Скиллинг (1951, стр. 157–159)
- ^ Хайт (1981, стр. 434–439)
- ^ Хайт (1981, стр. 434)
- ^ Рив (1995, стр. 558) harvtxt error: no target: CITEREFReeve1995 (help)
- ^ ab Chen (2004, стр. 26)
- ^ Финк, Дональд Г.; Битти, Х. Уэйн, ред. (1978), Стандартный справочник для инженеров-электриков (11-е изд.), McGraw Hill, стр. Таблица 18–21
- ^ Попович и Попович 1999, стр. 385
- ^ Син Нан и Салливан 2005
- ^ Центральный совет по производству электроэнергии (1982). Современная практика электростанций . Pergamon Press.
- ^ "Вращение углеродных нанотрубок порождает новые беспроводные приложения". Sciencedaily.com. 2009-03-09 . Получено 2011-11-08 .
- ^ ab Rahimi, A.; Yoon, Y.-K. (2016-03-16). «Исследование Cu/Ni нано-сверхрешеточных проводников для снижения потерь RF». IEEE Microwave and Wireless Components Letters . 26 (4): 258–260. doi :10.1109/LMWC.2016.2537780. ISSN 1531-1309. S2CID 30187468. Получено 22.12.2020 – через ResearchGate.
- ^ Хайт (1981, стр. 401)
- ^ Джексон (1999, стр. 353)
- ^ Фейнман (1964, стр. 32-11)
- ^ RG Chambers, Аномальный скин-эффект , Труды Лондонского королевского общества. Серия A, Математические и физические науки, т. 215, № 1123 (22 декабря 1952 г.), стр. 481–497 (17 страниц) https://www.jstor.org/stable/99095
- Чен, Уолтер Ю. (2004), Основы домашних сетей , Prentice Hall, ISBN 978-0-13-016511-4
- Фейнман, Ричард П.; Лейтон, Роберт Б.; Сэндс, Мэтью (1964). Лекции Фейнмана по физике, том 2. Эддисон-Уэсли. ISBN 0-201-02117-X.
- Хейт, Уильям (1981), Инженерная электромагнетика (4-е изд.), McGraw-Hill, ISBN 978-0-07-027395-5
- Джексон, Джон Дэвид (1999), Классическая электродинамика (3-е изд.), Wiley, ISBN 978-0471309321
- Джордан, Эдвард Конрад (1968), Электромагнитные волны и излучающие системы , Prentice Hall, ISBN 978-0-13-249995-8
- Нахин, Пол Дж. Оливер Хевисайд: Мудрец в одиночестве . Нью-Йорк: IEEE Press, 1988. ISBN 0-87942-238-6 .
- Попович, Зоя; Попович, Бранко (1999), Глава 20, Скин-эффект, Введение в электромагнетизм , Prentice-Hall, ISBN 978-0-201-32678-9
- Скиллинг, Хью Х. (1951), Линии электропередачи , McGraw-Hill
- Терман, Ф. Э. (1943), Справочник радиоинженера , Нью-Йорк: McGraw-Hill
- Вандер Ворст, Андре; Розен, Арье; Коцука, Ёдзи (2006), Взаимодействие радиочастот/микроволн с биологическими тканями , John Wiley and Sons, Inc., ISBN 978-0-471-73277-8
- Xi Nan; Sullivan, CR (2005). "Эквивалентная комплексная модель проницаемости для обмоток из литцендратной проволоки". Fourtieth IAS Annual Meeting. Conference Record of the 2005 Industry Applications Conference, 2005. Vol. 3. pp. 2229–2235. doi :10.1109/IAS.2005.1518758. ISBN 978-0-7803-9208-3. ISSN 0197-2618. S2CID 114947614.







































































