Комплексный анализ
Эта статья включает список общих ссылок , но в ней отсутствуют соответствующие встроенные цитаты . ( Март 2021 ) |
| Mathematical analysis → Complex analysis |
| Complex analysis |
|---|
 |
| Complex numbers |
| Complex functions |
|
| Basic theory |
| Geometric function theory |
| People |
Комплексный анализ , традиционно известный как теория функций комплексной переменной , является разделом математического анализа , который исследует функции комплексных чисел . Он полезен во многих разделах математики, включая алгебраическую геометрию , теорию чисел , аналитическую комбинаторику и прикладную математику , а также в физике , включая разделы гидродинамики , термодинамики , квантовой механики и теории твисторов . В более широком смысле, использование комплексного анализа также имеет приложения в таких областях техники, как ядерная , аэрокосмическая , машиностроительная и электротехническая . [1]
Поскольку дифференцируемая функция комплексной переменной равна суммарной функции, заданной ее рядом Тейлора (то есть она является аналитической ), комплексный анализ в частности занимается аналитическими функциями комплексной переменной, то есть голоморфными функциями . Понятие может быть распространено на функции нескольких комплексных переменных .
История

Комплексный анализ является одним из классических разделов математики, корни которого уходят в XVIII век и немного раньше. Среди важных математиков, связанных с комплексными числами, были Эйлер , Гаусс , Риман , Коши , Гёста Миттаг-Леффлер , Вейерштрасс и многие другие в XX веке. Комплексный анализ, в частности теория конформных отображений , имеет множество физических приложений и также используется в аналитической теории чисел . В наше время он стал очень популярен благодаря новому импульсу от комплексной динамики и изображений фракталов, полученных путем итерации голоморфных функций . Другое важное применение комплексного анализа — теория струн , которая исследует конформные инварианты в квантовой теории поля .
Комплексные функции

Комплексная функция — это функция от комплексных чисел до комплексных чисел. Другими словами, это функция, которая имеет (не обязательно собственное) подмножество комплексных чисел в качестве области определения и комплексные числа в качестве кодомены . Обычно предполагается, что комплексные функции имеют область определения, которая содержит непустое открытое подмножество комплексной плоскости .
Для любой комплексной функции значения из области определения и их образы в диапазоне можно разделить на действительную и мнимую части:
где все имеют реальные значения.
Другими словами, сложную функцию можно разложить на
- и
т.е. на две действительные функции ( , ) двух действительных переменных ( , ).
Аналогично, любая комплекснозначная функция f на произвольном множестве X ( изоморфна ему и, следовательно, в этом смысле, ему) может рассматриваться как упорядоченная пара двух вещественнозначных функций : (Re f , Im f ) или, альтернативно, как векторнозначная функция из X в
Некоторые свойства комплекснозначных функций (такие как непрерывность ) являются не более чем соответствующими свойствами векторных функций двух действительных переменных. Другие концепции комплексного анализа, такие как дифференцируемость , являются прямыми обобщениями аналогичных концепций для действительных функций, но могут иметь совершенно разные свойства. В частности, каждая дифференцируемая комплексная функция является аналитической (см. следующий раздел), а две дифференцируемые функции, равные в окрестности точки, равны на пересечении своих областей определения (если области определения связаны ). Последнее свойство является основой принципа аналитического продолжения , который позволяет расширить каждую действительную аналитическую функцию единственным способом для получения комплексной аналитической функции, областью определения которой является вся комплексная плоскость с конечным числом удаленных дуг кривой . Многие основные и специальные комплексные функции определяются таким образом, включая комплексную показательную функцию , комплексные логарифмические функции и тригонометрические функции .
Голоморфные функции
Комплексные функции, дифференцируемые в каждой точке открытого подмножества комплексной плоскости, называются голоморфными на . В контексте комплексного анализа производная от при определяется как [2]
На первый взгляд, это определение формально аналогично определению производной действительной функции. Однако комплексные производные и дифференцируемые функции ведут себя существенно по-разному по сравнению со своими действительными аналогами. В частности, для того, чтобы этот предел существовал, значение разностного отношения должно приближаться к одному и тому же комплексному числу, независимо от того, каким образом мы приближаемся в комплексной плоскости. Следовательно, комплексная дифференцируемость имеет гораздо более сильные последствия, чем вещественная дифференцируемость. Например, голоморфные функции бесконечно дифференцируемы , тогда как существование n- й производной не обязательно подразумевает существование ( n + 1)-й производной для действительных функций. Более того, все голоморфные функции удовлетворяют более сильному условию аналитичности , что означает, что функция в каждой точке своей области определения локально задана сходящимся степенным рядом. По сути, это означает, что функции, голоморфные на , могут быть сколь угодно хорошо аппроксимированы полиномами в некоторой окрестности каждой точки в . Это резко контрастирует с дифференцируемыми действительными функциями; существуют бесконечно дифференцируемые действительные функции, которые нигде не являются аналитическими; см . Неаналитическая гладкая функция § Гладкая функция, которая нигде не является действительно аналитической .
Большинство элементарных функций, включая показательную функцию , тригонометрические функции и все полиномиальные функции , соответствующим образом расширенные на комплексные аргументы как функции , голоморфны на всей комплексной плоскости, что делает их целыми функциями , в то время как рациональные функции , где p и q являются полиномами, голоморфны на областях, которые исключают точки, где q равно нулю. Такие функции, которые голоморфны всюду, за исключением набора изолированных точек , известны как мероморфные функции . С другой стороны, функции , и не являются голоморфными нигде на комплексной плоскости, как можно показать из их неспособности удовлетворять условиям Коши–Римана (см. ниже).
Важным свойством голоморфных функций является соотношение между частными производными их действительных и мнимых компонент, известное как условия Коши–Римана . Если , определяемое соотношением , где , голоморфно в области , то для всех ,
В терминах действительной и мнимой частей функции, u и v , это эквивалентно паре уравнений и , где нижние индексы указывают на частное дифференцирование. Однако условия Коши–Римана не характеризуют голоморфные функции без дополнительных условий непрерывности (см. теорему Лумана–Мэнхоффа ).
Голоморфные функции демонстрируют некоторые замечательные особенности. Например, теорема Пикара утверждает, что область значений целой функции может принимать только три возможных формы: , , или для некоторых . Другими словами, если два различных комплексных числа и не находятся в области значений целой функции , то является постоянной функцией. Более того, голоморфная функция на связном открытом множестве определяется ее ограничением на любое непустое открытое подмножество.
Конформная карта

В математике конформное отображение — это функция , которая локально сохраняет углы , но не обязательно длины.
Более формально, пусть и будут открытыми подмножествами . Функция называется конформной (или сохраняющей углы) в точке , если она сохраняет углы между направленными кривыми через , а также сохраняет ориентацию. Конформные отображения сохраняют как углы, так и формы бесконечно малых фигур, но не обязательно их размер или кривизну .
Конформное свойство может быть описано в терминах матрицы производной Якобиана преобразования координат . Преобразование является конформным, когда Якобиан в каждой точке является положительным скаляром, умноженным на матрицу вращения ( ортогональным с детерминантом 1). Некоторые авторы определяют конформность, включая отображения, меняющие ориентацию, якобианы которых могут быть записаны как любой скаляр, умноженный на любую ортогональную матрицу. [3]
Для отображений в двух измерениях (сохраняющие ориентацию) конформные отображения являются в точности локально обратимыми комплексными аналитическими функциями. В трех и более измерениях теорема Лиувилля резко ограничивает конформные отображения несколькими типами.
Понятие конформности естественным образом обобщается на отображения между римановыми или полуримановыми многообразиями .Основные результаты
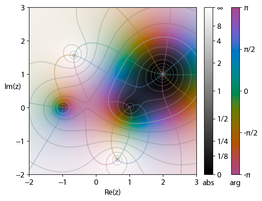
Оттенок представляет аргумент , яркость — величину.
Одним из центральных инструментов комплексного анализа является линейный интеграл . Линейный интеграл по замкнутому пути функции, которая голоморфна всюду внутри области, ограниченной замкнутым путем, всегда равен нулю, как утверждает интегральная теорема Коши . Значения такой голоморфной функции внутри круга можно вычислить с помощью интеграла по траектории на границе круга (как показано в интегральной формуле Коши ). Интегралы по траектории в комплексной плоскости часто используются для определения сложных действительных интегралов, и здесь применима, среди прочего, теория вычетов (см. методы контурного интегрирования ). «Полюс» (или изолированная сингулярность ) функции — это точка, в которой значение функции становится неограниченным или «взрывается». Если функция имеет такой полюс, то можно вычислить вычет функции там, который можно использовать для вычисления интегралов по траектории, включающих функцию; это содержание мощной теоремы о вычетах . Замечательное поведение голоморфных функций вблизи существенных сингулярностей описывается теоремой Пикара . Функции, имеющие только полюса, но не имеющие существенных особенностей, называются мероморфными . Ряды Лорана являются комплекснозначным эквивалентом рядов Тейлора , но могут использоваться для изучения поведения функций вблизи особенностей посредством бесконечных сумм более хорошо известных функций, таких как полиномы.
Ограниченная функция , голоморфная во всей комплексной плоскости, должна быть постоянной; это теорема Лиувилля . Ее можно использовать для предоставления естественного и короткого доказательства фундаментальной теоремы алгебры , которая утверждает, что поле комплексных чисел алгебраически замкнуто .
Если функция голоморфна во всей связной области, то ее значения полностью определяются ее значениями в любой меньшей подобласти. Говорят, что функция в большей области аналитически продолжена из ее значений в меньшей области. Это позволяет расширить определение функций, таких как дзета-функция Римана , которые изначально определяются в терминах бесконечных сумм, которые сходятся только в ограниченных областях, почти на всю комплексную плоскость. Иногда, как в случае натурального логарифма , невозможно аналитически продолжить голоморфную функцию в неодносвязную область в комплексной плоскости, но ее можно расширить до голоморфной функции на тесно связанной поверхности, известной как поверхность Римана .
Все это относится к комплексному анализу в одной переменной. Существует также очень богатая теория комплексного анализа в более чем одном комплексном измерении , в которой аналитические свойства, такие как разложение в степенной ряд, переносятся, тогда как большинство геометрических свойств голоморфных функций в одном комплексном измерении (таких как конформность ) не переносятся. Теорема об отображении Римана о конформном соотношении определенных областей в комплексной плоскости, которая может быть самым важным результатом в одномерной теории, резко терпит неудачу в более высоких измерениях.
Основное применение некоторых комплексных пространств — в квантовой механике в качестве волновых функций .
Смотрите также
- Сложная геометрия
- Гиперкомплексный анализ
- Векторные исчисления
- Список тем комплексного анализа
- Теорема монодромии
- Реальный анализ
- Теорема Римана–Роха
- Теорема Рунге
Ссылки
- ^ "Промышленные приложения комплексного анализа". Newton Gateway to Mathematics . 30 октября 2019 г. Получено 20 ноября 2023 г.
- ^ Рудин, Уолтер (1987). Действительный и комплексный анализ (PDF) . McGraw-Hill Education. стр. 197. ISBN 978-0-07-054234-1.
- ^ Блэр, Дэвид (2000-08-17). Теория инверсии и конформное отображение . Студенческая математическая библиотека. Том 9. Провиденс, Род-Айленд: Американское математическое общество. doi :10.1090/stml/009. ISBN 978-0-8218-2636-2. S2CID 118752074.
Источники
- Абловиц, М. Дж. и А. С. Фокас , Комплексные переменные: введение и применение (Кембридж, 2003).
- Альфорс, Л. , Комплексный анализ (McGraw-Hill, 1953).
- Картан, Х. , Элементарная теория аналитических функций комплексов переменных или плюсов. (Герман, 1961). Английский перевод, Элементарная теория аналитических функций одной или нескольких комплексных переменных. (Аддисон-Уэсли, 1963).
- Carathéodory, C. , Funktionentheorie. (Birkhäuser, 1950). Английский перевод, Теория функций комплексной переменной (Chelsea, 1954). [2 тома.]
- Кэрриер, Г. Ф. , М. Крук и К. Э. Пирсон, Функции комплексной переменной: теория и метод. (McGraw-Hill, 1966).
- Конвей, Дж. Б. , Функции одной комплексной переменной. (Springer, 1973).
- Фишер, С., Комплексные переменные. (Уодсворт и Брукс/Коул, 1990).
- Форсайт, А. , Теория функций комплексного переменного (Кембридж, 1893).
- Фрайтаг, Э. и Р. Бусам, Funktionentheorie . (Спрингер, 1995). Английский перевод, Комплексный анализ . (Спрингер, 2005).
- Гурса, Э. , Курс математического анализа, том 2. (Готье-Виллар, 1905). Английский перевод, Курс математического анализа, вып. 2, часть 1: Функции комплексной переменной. (Гинн, 1916).
- Хенрици, П. , Прикладной и вычислительный комплексный анализ (Wiley). [Три тома: 1974, 1977, 1986.]
- Крейциг, Э. , Высшая инженерная математика. (Wiley, 1962).
- Лаврентьев М. и Б. Шабат, Методы рассмотрения функций комплексного переменного. ( Методы теории функций комплексного переменного ). (1951, на русском языке).
- Маркушевич, А.И. Теория функций комплексного переменного , (Prentice-Hall, 1965). [Три тома.]
- Марсден и Хоффман, Базовый комплексный анализ. (Фримен, 1973).
- Нидхэм, Т. , Визуальный комплексный анализ. (Оксфорд, 1997). http://usf.usfca.edu/vca/
- Реммерт, Р. , Теория комплексных функций . (Springer, 1990).
- Рудин, В. , Действительный и комплексный анализ. (McGraw-Hill, 1966).
- Шоу, У.Т., Комплексный анализ с помощью Mathematica (Кембридж, 2006).
- Стайн, Э. и Р. Шакарчи, Комплексный анализ. (Принстон, 2003).
- Свешников А.Г. , Тихонов А.Н. Теория функций комплексной переменной. (Наука, 1967). Английский перевод, Теория функций комплексного переменного (МИР, 1978).
- Титчмарш, Э. К. , Теория функций. (Оксфорд, 1932).
- Вегерт Э. Визуальные сложные функции . (Биркхойзер, 2012).
- Уиттекер, Э. Т. и Г. Н. Уотсон , Курс современного анализа . (Кембридж, 1902). 3-е изд. (1920)
Внешние ссылки
- Страница комплексного анализа MathWorld от Wolfram Research










































