Конденсатор
.jpg/440px-Capacitors_(7189597135).jpg) | |
| Тип | Электронный компонент |
|---|---|
| Принцип работы | Емкость |
| Изобретенный | Эвальд Георг фон Клейст (1745 г.) Питер ван Мюсшенбрук (1746 г.) |
| Электронный символ | |
 | |
В электротехнике конденсатор — это устройство, которое хранит электрическую энергию , накапливая электрические заряды на двух близко расположенных поверхностях, которые изолированы друг от друга. Первоначально конденсатор был известен как конденсатор , [ 1 ] этот термин все еще встречается в нескольких составных названиях, таких как конденсаторный микрофон . Это пассивный электронный компонент с двумя клеммами .
Полезность конденсатора зависит от его емкости . Хотя между любыми двумя электрическими проводниками, расположенными поблизости в цепи , существует некоторая емкость, конденсатор — это компонент, специально разработанный для добавления емкости к некоторой части цепи.
Физическая форма и конструкция практических конденсаторов сильно различаются, и широко используются многие типы конденсаторов . Большинство конденсаторов содержат по крайней мере два электрических проводника , часто в виде металлических пластин или поверхностей, разделенных диэлектрической средой. Проводником может быть фольга, тонкая пленка, спеченный шарик металла или электролит . Непроводящий диэлектрик увеличивает зарядную емкость конденсатора. Материалы, обычно используемые в качестве диэлектриков, включают стекло , керамику , пластиковую пленку , бумагу , слюду , воздух и оксидные слои . Когда разность электрических потенциалов ( напряжение ) прикладывается к клеммам конденсатора, например, когда конденсатор подключен к батарее, через диэлектрик возникает электрическое поле , в результате чего на одной пластине собирается чистый положительный заряд , а на другой — чистый отрицательный заряд. Фактически через идеальный диэлектрик ток не течет . Однако через цепь источника идет поток заряда. Если это состояние сохраняется достаточно долго, ток через цепь источника прекращается. Если к выводам конденсатора приложено изменяющееся во времени напряжение, источник испытывает постоянный ток из-за циклов зарядки и разрядки конденсатора.
Конденсаторы широко используются в качестве частей электрических цепей во многих обычных электрических устройствах. В отличие от резистора , идеальный конденсатор не рассеивает энергию, хотя реальные конденсаторы рассеивают небольшое количество (см. Неидеальное поведение).
Самые ранние формы конденсаторов были созданы в 1740-х годах, когда европейские экспериментаторы обнаружили, что электрический заряд может храниться в стеклянных банках, заполненных водой, которые стали известны как лейденские банки . Сегодня конденсаторы широко используются в электронных схемах для блокировки постоянного тока , позволяя проходить переменному току . В аналоговых фильтровых сетях они сглаживают выход источников питания . В резонансных контурах они настраивают радиоприемники на определенные частоты . В системах передачи электроэнергии они стабилизируют напряжение и поток мощности. [2] Свойство накопления энергии в конденсаторах использовалось в качестве динамической памяти в ранних цифровых компьютерах, [3] и до сих пор используется в современных DRAM .
История
Естественные конденсаторы существуют с доисторических времен. Наиболее распространенным примером естественной емкости являются статические заряды, накопленные между облаками в небе и поверхностью Земли, где воздух между ними служит диэлектриком. Это приводит к разрядам молний , когда превышается пробивное напряжение воздуха. [4]

В октябре 1745 года Эвальд Георг фон Клейст из Померании , Германия, обнаружил, что заряд можно хранить, подключив высоковольтный электростатический генератор проводом к объему воды в стеклянной банке, которую он держал в руке. [5] Рука фон Клейста и вода действовали как проводники, а банка как диэлектрик (хотя детали механизма в то время были неправильно идентифицированы). Фон Клейст обнаружил, что прикосновение к проводу приводило к мощной искре, гораздо более болезненной, чем та, что получалась от электростатической машины. В следующем году голландский физик Питер ван Мушенбрук изобрел похожий конденсатор, который был назван Лейденской банкой , в честь Лейденского университета , где он работал. [6] Он также был впечатлен силой полученного им удара, написав: «Я бы не выдержал второго удара даже за королевство Франции». [7]
Дэниел Грэлат был первым, кто объединил несколько банок параллельно, чтобы увеличить емкость хранения заряда. [8] Бенджамин Франклин исследовал лейденскую банку и пришел к выводу, что заряд хранится на стекле, а не в воде, как предполагали другие. Он также принял термин «батарея», [9] [10] (обозначающий увеличение мощности с рядом подобных единиц, как в батарее пушек ), впоследствии примененный к кластерам электрохимических ячеек . [11] В 1747 году лейденские банки были изготовлены путем покрытия внутренней и внешней части банок металлической фольгой, оставляя пространство у горлышка, чтобы предотвратить возникновение дуги между фольгой. [12] Самой ранней единицей емкости была банка , эквивалентная примерно 1,11 нанофарад . [13]
Лейденские банки или более мощные устройства, использующие плоские стеклянные пластины, чередующиеся с фольгированными проводниками, использовались исключительно вплоть до 1900 года, когда изобретение беспроводной связи ( радио ) создало спрос на стандартные конденсаторы, а устойчивый переход к более высоким частотам потребовал конденсаторов с меньшей индуктивностью . Стали использоваться более компактные методы строительства, такие как гибкий диэлектрический лист (например, промасленная бумага), зажатый между листами металлической фольги, свернутый или сложенный в небольшой пакет.

Ранние конденсаторы были известны как конденсаторы , термин, который иногда используется и сегодня, особенно в мощных приложениях, таких как автомобильные системы. Термин condensatore был использован Алессандро Вольтой в 1780 году для обозначения устройства, похожего на его электрофорус , который он разработал для измерения электричества, и переведен в 1782 году как конденсатор , [14] где название относилось к способности устройства хранить более высокую плотность электрического заряда, чем это было возможно с изолированным проводником. [15] [1] Термин стал устаревшим из-за неоднозначного значения парового конденсатора , и с 1926 года в Великобритании рекомендуемым термином стал конденсатор , [16] в то время как в Соединенных Штатах это изменение произошло значительно позже.
С самого начала изучения электричества непроводящие материалы, такие как стекло , фарфор , бумага и слюда, использовались в качестве изоляторов . Спустя десятилетия эти материалы также хорошо подходили для использования в качестве диэлектрика для первых конденсаторов. Бумажные конденсаторы, изготовленные путем прокладывания полоски пропитанной бумаги между полосками металла и сворачивания результата в цилиндр, широко использовались в конце 19 века; их производство началось в 1876 году, [17] и они использовались с начала 20 века в качестве развязывающих конденсаторов в телефонии .
Фарфор использовался в первых керамических конденсаторах . В первые годы существования беспроводного передающего аппарата Маркони фарфоровые конденсаторы использовались для высоковольтных и высокочастотных приложений в передатчиках . На стороне приемника меньшие слюдяные конденсаторы использовались для резонансных цепей . Слюдяные конденсаторы были изобретены в 1909 году Уильямом Дубилье. До Второй мировой войны слюда была наиболее распространенным диэлектриком для конденсаторов в Соединенных Штатах. [17]
Чарльз Поллак (настоящее имя Кароль Поллак ), изобретатель первых электролитических конденсаторов , обнаружил, что оксидный слой на алюминиевом аноде оставался стабильным в нейтральном или щелочном электролите , даже при отключении питания. В 1896 году он получил патент США № 672,913 на «Электрический жидкостный конденсатор с алюминиевыми электродами». Твердоэлектролитные танталовые конденсаторы были изобретены Bell Laboratories в начале 1950-х годов как миниатюрный и более надежный низковольтный опорный конденсатор для дополнения их недавно изобретенного транзистора .
С развитием пластиковых материалов органическими химиками во время Второй мировой войны , конденсаторная промышленность начала заменять бумагу более тонкими полимерными пленками. Одна из самых ранних разработок в области пленочных конденсаторов была описана в британском патенте 587,953 в 1944 году. [17]
Электрические двухслойные конденсаторы (теперь суперконденсаторы ) были изобретены в 1957 году, когда Х. Беккер разработал «Низковольтный электролитический конденсатор с пористыми углеродными электродами». [17] [18] [19] Он считал, что энергия хранится в виде заряда в углеродных порах, используемых в его конденсаторе, как и в порах протравленной фольги электролитических конденсаторов. Поскольку механизм двойного слоя в то время ему не был известен, он написал в патенте: «Неизвестно точно, что происходит в компоненте, если он используется для хранения энергии, но это приводит к чрезвычайно высокой емкости».
Конденсатор МОП позже был широко принят в качестве накопительного конденсатора в микросхемах памяти и в качестве основного строительного блока прибора с зарядовой связью (ПЗС) в технологии датчиков изображения . [20] В 1966 году доктор Роберт Деннард изобрел современную архитектуру DRAM, объединив один МОП-транзистор на конденсатор. [21] [22]
Теория работы
Обзор


Конденсатор состоит из двух проводников , разделенных непроводящей областью. [23] Непроводящая область может быть либо вакуумом , либо электроизоляционным материалом, известным как диэлектрик . Примерами диэлектрических сред являются стекло, воздух, бумага, пластик, керамика и даже обедненная полупроводником область , химически идентичная проводникам. По закону Кулона заряд на одном проводнике будет оказывать силу на носители заряда внутри другого проводника, притягивая заряд противоположной полярности и отталкивая заряды одинаковой полярности, таким образом, на поверхности другого проводника будет индуцироваться заряд противоположной полярности. Таким образом, проводники удерживают равные и противоположные заряды на своих обращенных друг к другу поверхностях, [24] и диэлектрик создает электрическое поле.
Идеальный конденсатор характеризуется постоянной емкостью C , в фарадах в системе единиц СИ , определяемой как отношение положительного или отрицательного заряда Q на каждом проводнике к напряжению V между ними: [23] Емкость в один фарад (Ф) означает, что один кулон заряда на каждом проводнике вызывает напряжение в один вольт на устройстве. [25] Поскольку проводники (или пластины) расположены близко друг к другу, противоположные заряды на проводниках притягиваются друг к другу из-за их электрических полей, что позволяет конденсатору хранить больше заряда для данного напряжения, чем когда проводники разделены, что дает большую емкость.
В практических устройствах накопление заряда иногда воздействует на конденсатор механически, вызывая изменение его емкости. В этом случае емкость определяется в терминах инкрементных изменений:
Гидравлическая аналогия

В гидравлической аналогии напряжение аналогично давлению воды, а электрический ток через провод аналогичен потоку воды через трубу. Конденсатор подобен эластичной диафрагме внутри трубы. Хотя вода не может пройти через диафрагму, она движется, когда диафрагма растягивается или не растягивается.
- Емкость аналогична упругости диафрагмы . Точно так же, как отношение разности зарядов к напряжению будет больше для большего значения емкости ( ), отношение вытеснения воды к давлению будет больше для диафрагмы, которая легче изгибается.
- В цепи переменного тока конденсатор ведет себя как диафрагма в трубе, позволяя заряду перемещаться по обе стороны диэлектрика, в то время как электроны фактически не проходят через него. Для цепей постоянного тока конденсатор аналогичен гидравлическому аккумулятору , сохраняя энергию до тех пор, пока давление не будет сброшено. Аналогично, они могут использоваться для сглаживания потока электричества в выпрямленных цепях постоянного тока таким же образом, как аккумулятор гасит скачки напряжения от гидравлического насоса.
- Заряженные конденсаторы и растянутые диафрагмы хранят потенциальную энергию . Чем больше заряжен конденсатор, тем выше напряжение на пластинах ( ). Аналогично, чем больше вытесненный объем воды, тем больше упругая потенциальная энергия.
- Электрический ток влияет на разницу зарядов на конденсаторе так же, как поток воды влияет на разницу объемов на диафрагме.
- Подобно тому, как конденсаторы испытывают пробой диэлектрика под воздействием высокого напряжения, диафрагмы лопаются под действием экстремального давления.
- Так же, как конденсаторы блокируют постоянный ток, пропуская переменный ток, диафрагмы не вытесняют воду, если не происходит изменения давления.
Эквивалентность цепи при кратковременном и длительном пределе
В цепи конденсатор может вести себя по-разному в разные моменты времени. Однако обычно легко думать о кратковременном пределе и долговременном пределе:
- В долговременном пределе, после того как ток заряда/разряда насытит конденсатор, ток не будет поступать (или выходить) ни из одной из сторон конденсатора; поэтому долговременная эквивалентность конденсатора представляет собой разомкнутую цепь.
- В кратковременном пределе, если конденсатор начинает работать с определенного напряжения V, то, поскольку падение напряжения на конденсаторе в этот момент известно, мы можем заменить его идеальным источником напряжения с напряжением V. В частности, если V=0 (конденсатор не заряжен), кратковременным эквивалентом конденсатора является короткое замыкание.
Плоский конденсатор


Простейшая модель конденсатора состоит из двух тонких параллельных проводящих пластин, каждая из которых имеет площадь, разделенную равномерным зазором толщиной, заполненным диэлектриком с проницаемостью . Предполагается, что зазор намного меньше размеров пластин. Эта модель хорошо применима ко многим практическим конденсаторам, которые состоят из металлических листов, разделенных тонким слоем изолирующего диэлектрика, поскольку производители стараются поддерживать диэлектрик очень равномерным по толщине, чтобы избежать тонких пятен, которые могут привести к выходу конденсатора из строя.
Поскольку расстояние между пластинами равномерно по всей площади пластины, электрическое поле между пластинами постоянно и направлено перпендикулярно поверхности пластины, за исключением области вблизи краев пластин, где поле уменьшается, поскольку линии электрического поля «выступают» из сторон конденсатора. Эта область «крайнего поля» имеет примерно такую же ширину, что и расстояние между пластинами, , и, предполагая, что она мала по сравнению с размерами пластины, она достаточно мала, чтобы ее можно было проигнорировать. Поэтому, если заряд поместить на одну пластину и на другую пластину (ситуация для неравномерно заряженных пластин обсуждается ниже), заряд на каждой пластине будет равномерно распределен в поверхностном слое заряда с постоянной плотностью заряда кулонов на квадратный метр на внутренней поверхности каждой пластины. Из закона Гаусса величина электрического поля между пластинами равна . Напряжение (разность) между пластинами определяется как линейный интеграл электрического поля по линии (в направлении z) от одной пластины к другой. Емкость определяется как . Подставляя выше в это уравнение
Таким образом, в конденсаторе наибольшая емкость достигается при использовании диэлектрического материала с высокой диэлектрической проницаемостью , большой площади пластин и малом расстоянии между пластинами.
Поскольку площадь пластин увеличивается пропорционально квадрату линейных размеров, а расстояние между ними увеличивается линейно, емкость масштабируется пропорционально линейным размерам конденсатора ( ), или как кубический корень из объема.
Плоский конденсатор может хранить только конечное количество энергии, прежде чем произойдет пробой диэлектрика . Диэлектрический материал конденсатора имеет диэлектрическую прочность U d , которая устанавливает напряжение пробоя конденсатора на уровне V = V bd = U d d . Максимальная энергия, которую может хранить конденсатор, таким образом, равна
Максимальная энергия является функцией диэлектрического объема, диэлектрической проницаемости и диэлектрической прочности . Изменение площади пластин и расстояния между пластинами при сохранении того же объема не приводит к изменению максимального количества энергии, которое может хранить конденсатор, пока расстояние между пластинами остается намного меньше, чем длина и ширина пластин. Кроме того, эти уравнения предполагают, что электрическое поле полностью сосредоточено в диэлектрике между пластинами. В действительности существуют краевые поля вне диэлектрика, например, между сторонами пластин конденсатора, которые увеличивают эффективную емкость конденсатора. Это иногда называют паразитной емкостью . Для некоторых простых геометрий конденсатора этот дополнительный член емкости можно рассчитать аналитически. [26] Он становится пренебрежимо малым, когда отношения ширины пластины к разделению и длины к разделению велики.
Для неравномерно заряженных пластин:
- Если одна пластина заряжена, а другая заряжена , и если обе пластины отделены от других материалов в окружающей среде, то внутренняя поверхность первой пластины будет иметь , а внутренняя поверхность второй пластины будет иметь заряд. [ необходима цитата ] Таким образом, напряжение между пластинами равно . Обратите внимание, что внешняя поверхность обеих пластин будет иметь , но эти заряды не влияют на напряжение между пластинами.
- Если одна пластина заряжена , а другая заряжена , и если вторая пластина соединена с землей, то внутренняя поверхность первой пластины будет иметь , а внутренняя поверхность второй пластины будет иметь . Таким образом, напряжение между пластинами равно . Обратите внимание, что внешняя поверхность обеих пластин будет иметь нулевой заряд.
Конденсатор с чередованием

Для количества пластин в конденсаторе общая емкость будет равна, где — емкость одной пластины, а — количество чередующихся пластин.
Как показано на рисунке справа, чередующиеся пластины можно рассматривать как параллельные пластины, соединенные друг с другом. Каждая пара соседних пластин действует как отдельный конденсатор; число пар всегда на единицу меньше числа пластин, отсюда и множитель.
Энергия, запасенная в конденсаторе
Чтобы увеличить заряд и напряжение на конденсаторе, работа должна быть выполнена внешним источником энергии для перемещения заряда с отрицательной на положительную пластину против противодействующей силы электрического поля. [27] [28] Если напряжение на конденсаторе равно , работа, необходимая для перемещения небольшого приращения заряда с отрицательной на положительную пластину, равна . Энергия хранится в увеличенном электрическом поле между пластинами. Полная энергия, хранящаяся в конденсаторе (выраженная в джоулях ), равна полной работе, выполненной для создания электрического поля из незаряженного состояния. [29] [28] [27] где — заряд, хранящийся в конденсаторе, — напряжение на конденсаторе, — емкость. Эта потенциальная энергия будет оставаться в конденсаторе до тех пор, пока заряд не будет удален. Если заряду позволить переместиться обратно с положительной на отрицательную пластину, например, путем подключения цепи с сопротивлением между пластинами, заряд, движущийся под действием электрического поля, будет выполнять работу во внешней цепи.
Если зазор между пластинами конденсатора постоянен, как в модели параллельных пластин выше, электрическое поле между пластинами будет однородным (пренебрегая краевыми полями) и будет иметь постоянное значение . В этом случае запасенная энергия может быть рассчитана из напряженности электрического поля. Последняя формула выше равна плотности энергии на единицу объема в электрическом поле, умноженной на объем поля между пластинами, что подтверждает, что энергия в конденсаторе запасается в его электрическом поле.
Зависимость тока от напряжения

Ток I ( t ) через любой компонент в электрической цепи определяется как скорость потока заряда Q ( t ), проходящего через него. Фактические заряды – электроны – не могут проходить через диэлектрик идеального конденсатора . [примечание 1] Вместо этого один электрон накапливается на отрицательной пластине для каждого, который покидает положительную пластину, что приводит к истощению электронов и последующему положительному заряду на одном электроде, который равен и противоположен накопленному отрицательному заряду на другом. Таким образом, заряд на электродах равен интегралу тока , а также пропорционален напряжению, как обсуждалось выше. Как и в случае с любой первообразной , добавляется константа интегрирования для представления начального напряжения V ( t0 ). Это интегральная форма уравнения конденсатора: [ 30 ]
Взяв производную от этого и умножив на C, получаем производную форму: [31] для C, не зависящую от времени, напряжения и электрического заряда.
Двойником конденсатора является индуктор , который хранит энергию в магнитном поле , а не в электрическом. Его зависимость тока от напряжения получается путем замены тока и напряжения в уравнениях конденсатора и замены C на индуктивность L.
Цепи постоянного тока

Последовательная цепь, содержащая только резистор , конденсатор, переключатель и постоянный источник постоянного тока с напряжением V 0 , известна как цепь зарядки . [32] Если конденсатор изначально не заряжен, а переключатель открыт, а переключатель закрыт при t = 0 , то из закона напряжения Кирхгофа следует , что
Взяв производную и умножив на C , получаем дифференциальное уравнение первого порядка :
При t = 0 напряжение на конденсаторе равно нулю, а напряжение на резисторе равно V 0 . Тогда начальный ток равен I (0) = V 0 / R . При таком предположении решение дифференциального уравнения дает где τ 0 = RC — постоянная времени системы. Когда конденсатор достигает равновесия с напряжением источника, напряжение на резисторе и ток через всю цепь экспоненциально убывают . В случае разряжающегося конденсатора начальное напряжение конденсатора ( V Ci ) заменяет V 0 . Уравнения становятся
Цепи переменного тока
Импеданс , векторная сумма реактивного сопротивления и сопротивления , описывает разность фаз и отношение амплитуд между синусоидально изменяющимся напряжением и синусоидально изменяющимся током на заданной частоте. Анализ Фурье позволяет построить любой сигнал из спектра частот, откуда можно найти реакцию схемы на различные частоты. Реактивное сопротивление и импеданс конденсатора равны соответственно , где j — мнимая единица , а ω — угловая частота синусоидального сигнала. Фаза − j указывает на то, что переменное напряжение V = ZI отстает от переменного тока на 90°: положительная фаза тока соответствует увеличению напряжения по мере зарядки конденсатора; нулевой ток соответствует мгновенному постоянному напряжению и т. д.
Импеданс уменьшается с увеличением емкости и частоты. [33] Это означает, что более высокочастотный сигнал или больший конденсатор приводят к более низкой амплитуде напряжения на амплитуду тока – «короткое замыкание» переменного тока или связь по переменному току . И наоборот, для очень низких частот реактивное сопротивление велико, так что конденсатор является почти разомкнутой цепью в анализе переменного тока – эти частоты были «отфильтрованы».
Конденсаторы отличаются от резисторов и катушек индуктивности тем, что их полное сопротивление обратно пропорционально определяющей характеристике, то есть емкости .
Конденсатор, подключенный к источнику переменного напряжения, имеет ток смещения, протекающий через него. В случае, если источником напряжения является V 0 cos(ωt), ток смещения можно выразить как:
При sin( ωt ) = −1 конденсатор имеет максимальный (или пиковый) ток, при котором I 0 = ωCV 0 . Отношение пикового напряжения к пиковому току обусловлено емкостным сопротивлением (обозначаемым X C ).
X C стремится к нулю, когда ω стремится к бесконечности. Если X C стремится к 0, конденсатор напоминает короткий провод, который сильно пропускает ток на высоких частотах. X C стремится к бесконечности, когда ω стремится к нулю. Если X C стремится к бесконечности, конденсатор напоминает разомкнутую цепь, которая плохо пропускает низкие частоты.
Ток конденсатора можно выразить в виде косинуса для лучшего сравнения с напряжением источника:
В этой ситуации ток сдвинут по фазе относительно напряжения на +π/2 радиан или +90 градусов, т.е. ток опережает напряжение на 90°.
Анализ цепи Лапласа (s-область)
При использовании преобразования Лапласа в анализе цепей импеданс идеального конденсатора без начального заряда представляется в s -области следующим образом: где
- C — емкость, а
- s — комплексная частота.
Анализ схемы
- Для конденсаторов параллельно


- Конденсаторы в параллельной конфигурации имеют одинаковое приложенное напряжение. Их емкости складываются. Заряд распределяется между ними по размеру. Используя схематическую диаграмму для визуализации параллельных пластин, становится очевидным, что каждый конденсатор вносит вклад в общую площадь поверхности.
- Для конденсаторов последовательно

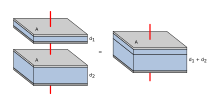
- При последовательном соединении принципиальная схема показывает, что расстояние разделения, а не площадь пластины, суммируется. Каждый конденсатор хранит мгновенное накопление заряда, равное накоплению заряда любого другого конденсатора в серии. Общая разность напряжений от конца до конца распределяется на каждый конденсатор в соответствии с обратной величиной его емкости. Вся серия действует как конденсатор, меньший, чем любой из ее компонентов.
- Конденсаторы объединяются последовательно для достижения более высокого рабочего напряжения, например, для сглаживания высоковольтного источника питания. Номинальные напряжения, которые основаны на разделении пластин, складываются, если емкость и токи утечки для каждого конденсатора идентичны. В таком применении, в некоторых случаях, последовательные цепочки соединяются параллельно, образуя матрицу. Цель состоит в том, чтобы максимизировать накопление энергии в сети без перегрузки какого-либо конденсатора. Для накопления высокой энергии с конденсаторами последовательно необходимо применять некоторые меры безопасности, чтобы гарантировать, что один конденсатор выйдет из строя и ток утечки не будет подавать слишком большое напряжение на другие последовательные конденсаторы.
- Последовательное соединение иногда используется также для адаптации поляризованных электролитических конденсаторов к использованию в биполярном переменном токе.
- Распределение напряжения в параллельно-последовательных сетях.
- Чтобы смоделировать распределение напряжений от одного заряженного конденсатора, подключенного параллельно к цепочке последовательных конденсаторов :
- Примечание: это верно только в том случае, если все значения емкости равны.
- Мощность, передаваемая в этом соглашении, составляет:
Неидеальное поведение
На практике конденсаторы отклоняются от идеального уравнения конденсатора в нескольких аспектах. Некоторые из них, такие как ток утечки и паразитные эффекты, являются линейными или могут быть проанализированы как почти линейные и могут быть учтены путем добавления виртуальных компонентов для формирования эквивалентной схемы. Затем могут быть применены обычные методы анализа сети . [34] В других случаях, таких как с напряжением пробоя, эффект нелинейный и обычный (нормальный, например, линейный) анализ сети не может быть использован, эффект должен рассматриваться отдельно. Еще одна группа артефактов может существовать, включая температурную зависимость, которая может быть линейной, но делает недействительным предположение в анализе о том, что емкость является постоянной величиной. Наконец, комбинированные паразитные эффекты, такие как внутренняя индуктивность, сопротивление или диэлектрические потери, могут демонстрировать неоднородное поведение при различных частотах работы.
Напряжение пробоя
Выше определенной напряженности электрического поля, известной как диэлектрическая прочность E ds , диэлектрик в конденсаторе становится проводящим. Напряжение, при котором это происходит, называется напряжением пробоя устройства и определяется произведением диэлектрической прочности и расстояния между проводниками, [35]
Максимальная энергия, которая может безопасно храниться в конденсаторе, ограничена напряжением пробоя. Превышение этого напряжения может привести к короткому замыканию между пластинами, что часто может привести к необратимому повреждению диэлектрика, пластин или и того, и другого. Из-за масштабирования емкости и напряжения пробоя с толщиной диэлектрика все конденсаторы, изготовленные с определенным диэлектриком, имеют приблизительно одинаковую максимальную плотность энергии , в той степени, в которой диэлектрик доминирует над их объемом. [36]
Для воздушных диэлектрических конденсаторов напряженность поля пробоя составляет порядка 2–5 МВ/м (или кВ/мм); для слюды пробой составляет 100–300 МВ/м; для масла — 15–25 МВ/м; она может быть намного меньше, если для диэлектрика используются другие материалы. [37] Диэлектрик используется в очень тонких слоях, поэтому абсолютное напряжение пробоя конденсаторов ограничено. Типичные номинальные значения для конденсаторов, используемых в общих электронных приложениях, варьируются от нескольких вольт до 1 кВ. По мере увеличения напряжения диэлектрик должен быть толще, что делает высоковольтные конденсаторы более крупными по емкости, чем те, которые рассчитаны на более низкие напряжения.
Напряжение пробоя критически зависит от таких факторов, как геометрия проводящих частей конденсатора; острые края или точки увеличивают напряженность электрического поля в этой точке и могут привести к локальному пробою. Как только это начинает происходить, пробой быстро проходит через диэлектрик, пока не достигнет противоположной пластины, оставляя углерод позади и вызывая короткое замыкание (или относительно низкоомную) цепь. Результаты могут быть взрывоопасными, так как короткое замыкание в конденсаторе потребляет ток из окружающей схемы и рассеивает энергию. [38] Однако в конденсаторах с определенными диэлектриками [39] [40] и тонкими металлическими электродами короткие замыкания не образуются после пробоя. Это происходит потому, что металл плавится или испаряется в области пробоя, изолируя его от остальной части конденсатора. [41] [42]
Обычный путь пробоя заключается в том, что напряженность поля становится достаточно большой, чтобы вытянуть электроны в диэлектрике из их атомов, тем самым вызывая проводимость. Возможны и другие сценарии, такие как примеси в диэлектрике, и, если диэлектрик имеет кристаллическую природу, дефекты в кристаллической структуре могут привести к лавинному пробою, как это наблюдается в полупроводниковых приборах. Напряжение пробоя также зависит от давления, влажности и температуры. [43]
Эквивалентная схема
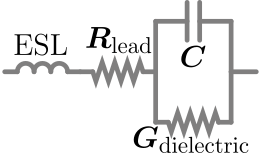
Идеальный конденсатор только хранит и высвобождает электрическую энергию, без рассеивания. На практике конденсаторы имеют недостатки в материалах конденсатора, которые приводят к следующим паразитным компонентам: [44]
- , эквивалентная последовательная индуктивность , обусловленная выводами. Обычно она имеет значение только на относительно высоких частотах.
- Два сопротивления, которые добавляют действительную составляющую к общему импедансу, что приводит к потере мощности:
- , небольшое последовательное сопротивление в выводах . Становится более актуальным по мере увеличения частоты.
- , малая проводимость (или, наоборот, большое сопротивление) параллельно емкости, чтобы учесть несовершенство диэлектрического материала. Это вызывает небольшой ток утечки через диэлектрик (см. § Утечка) [45] , который медленно разряжает конденсатор с течением времени. Эта проводимость доминирует над общим сопротивлением на очень низких частотах. Ее значение сильно варьируется в зависимости от материала и качества конденсатора. [ необходима цитата ]
Упрощенная модель серии RLC


С ростом частоты емкостное сопротивление (отрицательное реактивное сопротивление) уменьшается, поэтому проводимость диэлектрика становится менее важной, а последовательные компоненты становятся более значимыми. Таким образом, упрощенная модель серии RLC, действительная для большого диапазона частот, просто рассматривает конденсатор как находящийся последовательно с эквивалентной последовательной индуктивностью и зависящим от частоты эквивалентным последовательным сопротивлением , которое мало меняется с частотой. В отличие от предыдущей модели, эта модель недействительна на постоянном токе и очень низких частотах, где это актуально.
Индуктивное сопротивление увеличивается с частотой. Поскольку его знак положительный, оно противодействует емкости.
На собственной частоте RLC-цепи индуктивность полностью нейтрализует емкость, поэтому общее реактивное сопротивление равно нулю. Поскольку общее сопротивление при является просто действительным значением , средняя рассеиваемая мощность достигает своего максимума В среднеквадратичное значение 2/СОЭ , где V RMS — среднеквадратичное (RMS) напряжение на конденсаторе.
На еще более высоких частотах индуктивное сопротивление доминирует, поэтому конденсатор ведет себя нежелательным образом как индуктор. Высокочастотная инженерия подразумевает учет индуктивности всех соединений и компонентов.
Q-фактор
Для упрощенной модели конденсатора как идеального конденсатора, соединенного последовательно с эквивалентным последовательным сопротивлением , добротность конденсатора (или Q ) представляет собой отношение величины его емкостного сопротивления к его сопротивлению на заданной частоте :
Фактор добротности является мерой его эффективности: чем выше фактор добротности конденсатора, тем ближе он приближается к поведению идеального конденсатора. Коэффициент рассеяния является его обратной величиной.
Пульсирующий ток
Пульсирующий ток — это переменный компонент источника питания (часто импульсного источника питания ), частота которого может быть постоянной или переменной. Пульсирующий ток вызывает выделение тепла внутри конденсатора из-за диэлектрических потерь, вызванных изменяющейся напряженностью поля вместе с током, протекающим через слаборезистивные линии питания или электролит в конденсаторе. Эквивалентное последовательное сопротивление (ESR) — это величина внутреннего последовательного сопротивления, которое можно добавить к идеальному конденсатору для моделирования этого.
Некоторые типы конденсаторов , в первую очередь танталовые и алюминиевые электролитические конденсаторы , а также некоторые пленочные конденсаторы имеют определенное номинальное значение максимального пульсирующего тока.
- Танталовые электролитические конденсаторы с твердым электролитом из диоксида марганца ограничены пульсирующим током и, как правило, имеют самые высокие показатели ESR в семействе конденсаторов. Превышение их пределов пульсации может привести к коротким замыканиям и сгоранию деталей.
- Алюминиевые электролитические конденсаторы, наиболее распространенный тип электролитических конденсаторов, страдают от сокращения срока службы при более высоких токах пульсации. Если ток пульсации превышает номинальное значение конденсатора, это может привести к взрывному отказу.
- Керамические конденсаторы, как правило, не имеют ограничений по току пульсации [ требуется ссылка ] и имеют одни из самых низких значений ESR.
- Пленочные конденсаторы имеют очень низкие показатели ESR, но превышение номинального пульсирующего тока может привести к деградации и отказам.
Нестабильность емкости
Емкость некоторых конденсаторов уменьшается по мере старения компонента. В керамических конденсаторах это вызвано деградацией диэлектрика. Тип диэлектрика, окружающая рабочая температура и температура хранения являются наиболее значимыми факторами старения, в то время как рабочее напряжение обычно оказывает меньшее влияние, т. е. обычная конструкция конденсатора заключается в минимизации коэффициента напряжения. Процесс старения можно обратить вспять, нагрев компонент выше точки Кюри . Старение происходит быстрее всего в начале срока службы компонента, и со временем устройство стабилизируется. [46] Электролитические конденсаторы стареют по мере испарения электролита [ сломанный якорь ] . В отличие от керамических конденсаторов, это происходит ближе к концу срока службы компонента.
Температурная зависимость емкости обычно выражается в частях на миллион (ppm) на °C. Обычно ее можно рассматривать как широко распространенную линейную функцию, но она может быть заметно нелинейной при экстремальных температурах. Температурный коэффициент может быть положительным или отрицательным, в зависимости в основном от диэлектрического материала. Некоторые, обозначенные как C0G/NP0, но называемые NPO , имеют несколько отрицательный коэффициент при одной температуре, положительный при другой и нулевой между ними. Такие компоненты могут быть указаны для цепей, критических по температуре. [47]
Конденсаторы, особенно керамические конденсаторы, и старые конструкции, такие как бумажные конденсаторы, могут поглощать звуковые волны, что приводит к микрофонному эффекту. Вибрация перемещает пластины, заставляя емкость изменяться, в свою очередь, вызывая переменный ток. Некоторые диэлектрики также генерируют пьезоэлектричество . Результирующие помехи особенно проблематичны в аудиоприложениях, потенциально вызывая обратную связь или непреднамеренную запись. При обратном микрофонном эффекте изменяющееся электрическое поле между пластинами конденсатора оказывает физическую силу, перемещая их как динамик. Это может генерировать слышимый звук, но истощает энергию и нагружает диэлектрик и электролит, если таковые имеются.
Реверс тока и напряжения
Реверсирование тока происходит, когда ток меняет направление. Реверсирование напряжения — это изменение полярности в цепи. Реверсирование обычно описывается как процент максимального номинального напряжения, который меняет полярность. В цепях постоянного тока это обычно меньше 100%, часто в диапазоне от 0 до 90%, тогда как в цепях переменного тока происходит 100% реверсирование.
В цепях постоянного тока и импульсных цепях на изменение полярности тока и напряжения влияет затухание системы . Изменение полярности напряжения встречается в цепях RLC, которые недостаточно затухают . Ток и напряжение меняют направление, образуя гармонический осциллятор между индуктивностью и емкостью. Ток и напряжение имеют тенденцию колебаться и могут менять направление несколько раз, причем каждый пик будет ниже предыдущего, пока система не достигнет равновесия. Это часто называют звоном . Для сравнения, критически затухающие или чрезмерно затухающие системы обычно не испытывают изменения полярности напряжения. Изменение полярности также встречается в цепях переменного тока, где пиковый ток одинаков в каждом направлении.
Для максимального срока службы конденсаторы обычно должны быть способны выдерживать максимальное количество реверсий, которые может испытать система. Цепь переменного тока испытывает 100% реверсию напряжения, в то время как недостаточно демпфированные цепи постоянного тока испытывают менее 100%. Реверсия создает избыточные электрические поля в диэлектрике, вызывает избыточный нагрев как диэлектрика, так и проводников и может значительно сократить ожидаемый срок службы конденсатора. Номиналы реверсии часто влияют на конструктивные соображения для конденсатора, от выбора диэлектрических материалов и номинальных напряжений до типов используемых внутренних соединений. [48]
Диэлектрическое поглощение
Конденсаторы, изготовленные из любого типа диэлектрического материала, демонстрируют некоторый уровень « диэлектрической абсорбции » или «пропитывания». При разрядке конденсатора и его отключении через короткое время может возникнуть напряжение из-за гистерезиса в диэлектрике. Этот эффект нежелателен в таких приложениях, как прецизионные схемы выборки и хранения или схемы синхронизации. Уровень абсорбции зависит от многих факторов, от конструктивных соображений до времени зарядки, поскольку абсорбция является процессом, зависящим от времени. Однако основным фактором является тип диэлектрического материала. Такие конденсаторы, как танталовая электролитическая или полисульфоновая пленка, демонстрируют относительно высокое поглощение, в то время как полистирол или тефлон допускают очень небольшие уровни поглощения. [49] В некоторых конденсаторах, где существуют опасные напряжения и энергии, например, в импульсных лампах , телевизорах , микроволновых печах и дефибрилляторах , диэлектрическая абсорбция может перезарядить конденсатор до опасных напряжений после того, как он был закорочен или разряжен. Любой конденсатор, содержащий более 10 джоулей энергии, обычно считается опасным, в то время как 50 джоулей и выше потенциально смертельны. Конденсатор может восстановить от 0,01 до 20% своего первоначального заряда в течение нескольких минут, позволяя, казалось бы, безопасному конденсатору стать на удивление опасным. [50] [51] [52] [53] [54]
Утечка
Ни один материал не является идеальным изолятором, поэтому все диэлектрики допускают утечку небольшого уровня тока, который можно измерить с помощью мегомметра . [55] Утечка эквивалентна резистору, включенному параллельно с конденсатором. Постоянное воздействие таких факторов, как тепло, механическое напряжение или влажность, может привести к ухудшению диэлектрика, что приведет к чрезмерной утечке, проблеме, часто наблюдаемой в старых схемах с электронными лампами, особенно там, где использовались промасленные бумажные и фольговые конденсаторы. Во многих схемах с электронными лампами межкаскадные соединительные конденсаторы используются для проведения переменного сигнала от пластины одной лампы к сетке цепи следующего каскада. Утечка конденсатора может привести к повышению напряжения в сетке цепи от его нормальной настройки смещения, вызывая чрезмерный ток или искажение сигнала в нижестоящей лампе. В усилителях мощности это может привести к тому, что пластины начнут светиться красным, а токоограничивающие резисторы перегреются или даже выйдут из строя. Аналогичные соображения применимы к твердотельным (транзисторным) усилителям, изготовленным из компонентов, но благодаря меньшему выделению тепла и использованию современных полиэфирных диэлектрических барьеров эта некогда распространенная проблема стала относительно редкой.
Электролитический отказ из-за неиспользования
Алюминиевые электролитические конденсаторы кондиционируются при изготовлении путем приложения напряжения, достаточного для инициирования надлежащего внутреннего химического состояния. Это состояние поддерживается регулярным использованием оборудования. Если система, использующая электролитические конденсаторы, не используется в течение длительного периода времени, она может потерять свое кондиционирование . Иногда они выходят из строя из-за короткого замыкания при следующем использовании.
Продолжительность жизни
Все конденсаторы имеют разный срок службы в зависимости от их конструкции, условий эксплуатации и условий окружающей среды. Твердотельные керамические конденсаторы, как правило, имеют очень долгий срок службы при нормальном использовании, который мало зависит от таких факторов, как вибрация или температура окружающей среды, но такие факторы, как влажность, механическое напряжение и усталость , играют основную роль в их выходе из строя. Режимы выхода из строя могут различаться. Некоторые конденсаторы могут испытывать постепенную потерю емкости, повышенную утечку или увеличение эквивалентного последовательного сопротивления (ESR), в то время как другие могут выходить из строя внезапно или даже катастрофически . Например, металлопленочные конденсаторы более подвержены повреждениям от напряжения и влажности, но будут самовосстанавливаться, когда произойдет пробой диэлектрика. Образование тлеющего разряда в точке отказа предотвращает дугообразование, испаряя металлическую пленку в этом месте, нейтрализуя любое короткое замыкание с минимальной потерей емкости. Когда в пленке накапливается достаточное количество отверстий, в металлопленочном конденсаторе происходит полный отказ, как правило, происходящий внезапно без предупреждения.
Электролитические конденсаторы, как правило, имеют самый короткий срок службы. Электролитические конденсаторы очень мало подвержены вибрациям или влажности, но такие факторы, как температура окружающей среды и рабочая температура, играют большую роль в их выходе из строя, который постепенно происходит как увеличение ESR (до 300%) и до 20% уменьшения емкости. Конденсаторы содержат электролиты, которые в конечном итоге диффундируют через уплотнения и испаряются. Повышение температуры также увеличивает внутреннее давление и увеличивает скорость реакции химических веществ. Таким образом, срок службы электролитического конденсатора, как правило, определяется модификацией уравнения Аррениуса , которое используется для определения скоростей химических реакций:
Производители часто используют это уравнение для расчета ожидаемого срока службы в часах для электролитических конденсаторов при использовании при их расчетной рабочей температуре, на которую влияют как температура окружающей среды, ESR, так и пульсирующий ток. Однако эти идеальные условия могут не существовать при каждом использовании. Правило большого пальца для прогнозирования срока службы при различных условиях использования определяется:
Это означает, что срок службы конденсатора уменьшается вдвое при повышении температуры на каждые 10 градусов Цельсия, [56] где:
- номинальный срок службы в номинальных условиях, например 2000 часов
- номинальная максимальная/минимальная рабочая температура
- средняя рабочая температура
- ожидаемая продолжительность жизни при данных условиях
Типы конденсаторов
Практические конденсаторы доступны в продаже во многих различных формах. Тип внутреннего диэлектрика, структура пластин и корпус устройства сильно влияют на характеристики конденсатора и его применение.
Доступные значения варьируются от очень низких (диапазон пикофарад; хотя в принципе возможны и произвольно низкие значения, ограничивающим фактором является паразитная емкость в любой цепи) до суперконденсаторов емкостью около 5 кФ .
Электролитические конденсаторы емкостью более 1 микрофарада обычно используются из-за их небольшого размера и низкой стоимости по сравнению с другими типами, если только их относительно низкая стабильность, срок службы и поляризованная природа не делают их непригодными. Суперконденсаторы очень большой емкости используют пористый электродный материал на основе углерода.
Диэлектрические материалы

Большинство конденсаторов имеют диэлектрическую прокладку, которая увеличивает их емкость по сравнению с воздухом или вакуумом. Чтобы максимизировать заряд, который может удерживать конденсатор, диэлектрический материал должен иметь как можно большую диэлектрическую проницаемость , а также как можно большее напряжение пробоя . Диэлектрик также должен иметь как можно меньшие потери с частотой.
Однако доступны конденсаторы с низким значением, имеющие высокий вакуум между пластинами, что позволяет работать при чрезвычайно высоком напряжении и низких потерях. Переменные конденсаторы с пластинами, открытыми для атмосферы, обычно использовались в схемах настройки радиоприемников. Более поздние конструкции используют полимерный фольгированный диэлектрик между подвижными и неподвижными пластинами, без значительного воздушного пространства между пластинами.
Доступно несколько твердых диэлектриков, включая бумагу , пластик , стекло , слюду и керамику . [17]
Бумага широко использовалась в старых конденсаторах и обеспечивает относительно высокие характеристики напряжения. Однако бумага впитывает влагу и была в значительной степени заменена конденсаторами из пластиковой пленки .
Большинство пластиковых пленок, используемых в настоящее время, обеспечивают лучшую стабильность и старение, чем такие старые диэлектрики, как промасленная бумага, что делает их полезными в схемах таймеров, хотя они могут быть ограничены относительно низкими рабочими температурами и частотами из-за ограничений используемой пластиковой пленки. Большие пластиковые пленочные конденсаторы широко используются в схемах подавления, схемах запуска двигателей и схемах коррекции коэффициента мощности .
Керамические конденсаторы, как правило, небольшие, дешевые и полезные для высокочастотных приложений, хотя их емкость сильно меняется в зависимости от напряжения и температуры, и они плохо стареют. Они также могут страдать от пьезоэлектрического эффекта. Керамические конденсаторы в целом классифицируются как диэлектрики класса 1 , которые имеют предсказуемое изменение емкости в зависимости от температуры, или диэлектрики класса 2 , которые могут работать при более высоком напряжении. Современная многослойная керамика обычно довольно мала, но некоторые типы имеют изначально широкие допуски значений, проблемы микрофонного эффекта и обычно физически хрупкие.
Стеклянные и слюдяные конденсаторы чрезвычайно надежны, стабильны и устойчивы к высоким температурам и напряжениям, но слишком дороги для большинства массовых применений.
Электролитические конденсаторы и суперконденсаторы используются для хранения малых и больших объемов энергии соответственно, керамические конденсаторы часто используются в резонаторах , а паразитная емкость возникает в цепях, где простая структура проводник-изолятор-проводник формируется непреднамеренно конфигурацией схемы.


Электролитические конденсаторы используют алюминиевую или танталовую пластину с оксидным диэлектрическим слоем. Второй электрод представляет собой жидкий электролит , соединенный с цепью другой фольгированной пластиной. Электролитические конденсаторы обладают очень высокой емкостью, но страдают от плохих допусков, высокой нестабильности, постепенной потери емкости, особенно при воздействии тепла, и высокого тока утечки. Некачественные конденсаторы могут давать утечку электролита, что вредно для печатных плат. Проводимость электролита падает при низких температурах, что увеличивает эквивалентное последовательное сопротивление. Несмотря на широкое использование для кондиционирования электропитания, плохие высокочастотные характеристики делают их непригодными для многих приложений. Электролитические конденсаторы страдают от самодеградации, если не используются в течение определенного периода (около года), и при подаче полной мощности могут закоротить, что приводит к необратимому повреждению конденсатора и, как правило, к перегоранию предохранителя или выходу из строя выпрямительных диодов. Например, в старом оборудовании это может вызвать искрение в выпрямительных трубках. Их можно восстановить перед использованием, постепенно подавая рабочее напряжение, что часто выполняется на старинном ламповом оборудовании в течение тридцати минут с использованием переменного трансформатора для подачи переменного тока. Использование этой техники может быть менее удовлетворительным для некоторого твердотельного оборудования, которое может быть повреждено при работе ниже своего нормального диапазона мощности, требуя, чтобы источник питания был сначала изолирован от потребляющих цепей. Такие средства могут быть неприменимы к современным высокочастотным источникам питания, поскольку они выдают полное выходное напряжение даже при сниженном входном напряжении. [ необходима цитата ]
Танталовые конденсаторы обладают лучшими частотными и температурными характеристиками, чем алюминиевые, но имеют более высокую диэлектрическую абсорбцию и утечку. [57]
Полимерные конденсаторы (OS-CON, OC-CON, KO, AO) используют в качестве электролита твердый проводящий полимер (или полимеризованный органический полупроводник) и обеспечивают более длительный срок службы и более низкое эквивалентное последовательное сопротивление при более высокой стоимости, чем стандартные электролитические конденсаторы.
Проходной конденсатор — это компонент, который, хотя и не выполняет свою основную функцию, имеет емкость и используется для проведения сигналов через проводящий слой.
Для специальных применений доступно несколько других типов конденсаторов. Суперконденсаторы хранят большое количество энергии. Суперконденсаторы, изготовленные из углеродного аэрогеля , углеродных нанотрубок или высокопористых электродных материалов, обладают чрезвычайно высокой емкостью (до 5 кФ по состоянию на 2010 год [update]) и могут использоваться в некоторых приложениях вместо перезаряжаемых батарей . Конденсаторы переменного тока специально разработаны для работы в цепях переменного тока с линейным (сетевым) напряжением. Они обычно используются в цепях электродвигателей и часто рассчитаны на большие токи, поэтому они, как правило, имеют большие физические размеры. Обычно они прочно упакованы, часто в металлических корпусах, которые можно легко заземлить. Они также разработаны с напряжением пробоя постоянного тока, по крайней мере, в пять раз превышающим максимальное напряжение переменного тока.
Конденсаторы, зависящие от напряжения
Диэлектрическая проницаемость для ряда очень полезных диэлектриков изменяется в зависимости от приложенного электрического поля, например, сегнетоэлектрических материалов, поэтому емкость для этих устройств более сложная. Например, при зарядке такого конденсатора дифференциальное увеличение напряжения с зарядом регулируется: где зависимость емкости от напряжения, C ( V ) , предполагает, что емкость является функцией напряженности электрического поля, которая в устройстве с большой площадью параллельных пластин задается выражением ε = V / d . Это поле поляризует диэлектрик, поляризация которого в случае сегнетоэлектрика является нелинейной S -образной функцией электрического поля, которая в случае устройства с большой площадью параллельных пластин преобразуется в емкость, которая является нелинейной функцией напряжения. [58] [59]
В соответствии с зависимостью емкости от напряжения для заряда конденсатора до напряжения V найдено интегральное соотношение: которое согласуется с Q = CV только тогда, когда C не зависит от напряжения V.
Подобным же образом, энергия, запасенная в конденсаторе, теперь определяется выражением
Интегрирование: где используется смена порядка интегрирования .
Нелинейная емкость зонда микроскопа, сканирующего вдоль поверхности сегнетоэлектрика, используется для изучения доменной структуры сегнетоэлектрических материалов. [60]
Другой пример емкости, зависящей от напряжения, встречается в полупроводниковых приборах , таких как полупроводниковые диоды , где зависимость от напряжения возникает не из-за изменения диэлектрической проницаемости, а из-за зависимости от напряжения расстояния между зарядами на двух сторонах конденсатора. [61] Этот эффект намеренно используется в диодных приборах, известных как варикапы .
Частотно-зависимые конденсаторы
Если конденсатор управляется изменяющимся во времени напряжением, которое меняется достаточно быстро, на некоторой частоте поляризация диэлектрика не может следовать за напряжением. В качестве примера происхождения этого механизма внутренние микроскопические диполи, вносящие вклад в диэлектрическую проницаемость, не могут двигаться мгновенно, и поэтому с увеличением частоты приложенного переменного напряжения дипольный отклик ограничивается, а диэлектрическая проницаемость уменьшается. Изменение диэлектрической проницаемости с частотой называется диэлектрической дисперсией и регулируется процессами диэлектрической релаксации , такими как релаксация Дебая . В переходных условиях поле смещения можно выразить как (см. электрическая восприимчивость ):
указывая на задержку в ответе временной зависимостью ε r , вычисленной в принципе из базового микроскопического анализа, например, поведения диполя в диэлектрике. См., например, линейную функцию отклика . [62] [63] Интеграл распространяется на всю прошлую историю вплоть до настоящего времени. Преобразование Фурье во времени затем приводит к:
где ε r ( ω ) теперь является комплексной функцией , с мнимой частью, связанной с поглощением энергии поля средой. См. диэлектрическая проницаемость . Емкость, будучи пропорциональной диэлектрической постоянной, также демонстрирует это частотное поведение. Преобразование Фурье закона Гаусса с этой формой для поля смещения:
где j — мнимая единица , V ( ω ) — составляющая напряжения на угловой частоте ω , G ( ω ) — действительная часть тока, называемая проводимостью , а C ( ω ) определяет мнимую часть тока и является емкостью . Z ( ω ) — комплексное сопротивление.
Когда плоский конденсатор заполнен диэлектриком, измерение диэлектрических свойств среды основано на соотношении: где один штрих обозначает действительную часть, а двойной штрих — мнимую часть, Z ( ω ) — комплексное сопротивление с диэлектриком, C cmplx ( ω ) — так называемая комплексная емкость с диэлектриком, а C 0 — емкость без диэлектрика. [64] [65] (Измерение «без диэлектрика» в принципе означает измерение в свободном пространстве , что является недостижимой целью, поскольку даже квантовый вакуум , как предсказывают, демонстрирует неидеальное поведение, такое как дихроизм . Для практических целей, когда учитываются погрешности измерений, часто измерение в земном вакууме или просто расчет C 0 достаточно точны. [66] )
Используя этот метод измерения, диэлектрическая проницаемость может проявлять резонанс на определенных частотах, соответствующих характерным частотам отклика (энергиям возбуждения) вкладчиков диэлектрической проницаемости. Эти резонансы являются основой для ряда экспериментальных методов обнаружения дефектов. Метод проводимости измеряет поглощение как функцию частоты. [67] В качестве альтернативы, временной отклик емкости может быть использован напрямую, как в переходной спектроскопии глубокого уровня . [68]
Другой пример частотно-зависимой емкости возникает в случае с МОП-конденсаторами , где медленная генерация неосновных носителей означает, что на высоких частотах емкость измеряет только реакцию основных носителей, тогда как на низких частотах реагируют оба типа носителей. [61] [69]
На оптических частотах в полупроводниках диэлектрическая проницаемость демонстрирует структуру, связанную с зонной структурой твердого тела. Сложные методы измерения модуляционной спектроскопии, основанные на модуляции кристаллической структуры давлением или другими напряжениями и наблюдении связанных с этим изменений в поглощении или отражении света, продвинули наши знания об этих материалах. [70]
Стили

Расположение пластин и диэлектрика имеет множество вариаций в разных стилях в зависимости от желаемых номиналов конденсатора. Для небольших значений емкости (микрофарады и меньше) керамические диски используют металлические покрытия с проволочными выводами, прикрепленными к покрытию. Большие значения могут быть получены с помощью нескольких стопок пластин и дисков. Конденсаторы больших значений обычно используют металлическую фольгу или слой металлической пленки, нанесенный на поверхность диэлектрической пленки для изготовления пластин, и диэлектрическую пленку из пропитанной бумаги или пластика — они сворачиваются для экономии места. Чтобы уменьшить последовательное сопротивление и индуктивность для длинных пластин, пластины и диэлектрик располагаются в шахматном порядке так, чтобы соединение выполнялось на общем крае скрученных пластин, а не на концах полосок фольги или металлизированной пленки, которые составляют пластины.
Сборка заключена в оболочку, чтобы предотвратить попадание влаги в диэлектрик — в раннем радиооборудовании использовалась картонная трубка, запечатанная воском. Современные бумажные или пленочные диэлектрические конденсаторы окунаются в твердый термопластик. Большие конденсаторы для использования при высоком напряжении могут иметь рулонную форму, сжатую для размещения в прямоугольном металлическом корпусе, с болтовыми клеммами и втулками для соединений. Диэлектрик в больших конденсаторах часто пропитывается жидкостью для улучшения его свойств.

Конденсаторы могут иметь соединительные выводы, расположенные во многих конфигурациях, например, аксиально или радиально. «Аксиальный» означает, что выводы находятся на общей оси, обычно оси цилиндрического корпуса конденсатора – выводы выходят из противоположных концов. Радиальные выводы редко выровнены по радиусам окружности корпуса, поэтому этот термин является условным. Выводы (до изгиба) обычно находятся в плоскостях, параллельных плоскому корпусу конденсатора, и выходят в том же направлении; они часто параллельны при изготовлении.
Небольшие, дешевые дисковые керамические конденсаторы существуют с 1930-х годов и по-прежнему широко используются. После 1980-х годов широкое распространение получили корпуса для поверхностного монтажа конденсаторов. Эти корпуса чрезвычайно малы и не имеют соединительных выводов, что позволяет припаивать их непосредственно к поверхности печатных плат . Компоненты для поверхностного монтажа позволяют избежать нежелательных высокочастотных эффектов, обусловленных выводами, и упрощают автоматизированную сборку, хотя ручная обработка затруднена из-за их небольшого размера.
Механически управляемые переменные конденсаторы позволяют регулировать расстояние между пластинами, например, вращая или сдвигая набор подвижных пластин в соответствии с набором неподвижных пластин. Недорогие переменные конденсаторы сжимают вместе чередующиеся слои алюминия и пластика с помощью винта . Электрическое управление емкостью достигается с помощью варакторов (или варикапов), которые представляют собой полупроводниковые диоды с обратным смещением , ширина обедненной области которых изменяется в зависимости от приложенного напряжения. Они используются в контурах фазовой автоподстройки частоты , среди других применений.
Маркировка конденсаторов
Коды маркировки для более крупных деталей
Большинство конденсаторов имеют обозначения, напечатанные на их корпусах, которые указывают на их электрические характеристики. Большие конденсаторы, такие как электролитические типы, обычно отображают емкость как значение с явной единицей измерения, например, 220 мкФ .
По типографским причинам некоторые производители печатают на конденсаторах MF для обозначения микрофарад (мкФ). [71]
Трех-/четырехзначный код маркировки для небольших конденсаторов
Для меньших конденсаторов, таких как керамические, часто используется сокращенное обозначение, состоящее из трех цифр и необязательной буквы, где цифры ( XYZ ) обозначают емкость в пикофарадах (пФ), рассчитанную как XY × 10 Z , а буква указывает на допуск. Обычные допуски составляют ±5%, ±10% и ±20%, обозначаются как J, K и M соответственно.
Конденсатор также может быть маркирован с указанием его рабочего напряжения, температуры и других соответствующих характеристик.
Пример: Конденсатор, маркированный или обозначенный как 473K 330V, имеет емкость47 × 10 3 пФ = 47 нФ (±10%) при максимальном рабочем напряжении 330 В. Рабочее напряжение конденсатора — это номинально самое высокое напряжение, которое может быть приложено к нему без чрезмерного риска пробоя диэлектрического слоя.
Двухбуквенный код маркировки для малогабаритных конденсаторов
Для емкостей, следующих за сериями предпочтительных значений E3 , E6 , E12 или E24 , прежние стандарты ANSI/EIA-198-D:1991, ANSI/EIA-198-1-E:1998 и ANSI/EIA-198-1-F:2002, а также поправка IEC 60062:2016/AMD1:2019 к IEC 60062 определяют специальный двухсимвольный код маркировки для конденсаторов для очень маленьких деталей, которые не оставляют места для печати на них вышеупомянутого трех-/четырехсимвольного кода. Код состоит из заглавной буквы, обозначающей две значащие цифры значения, за которой следует цифра, обозначающая множитель. Стандарт EIA также определяет ряд строчных букв для указания ряда значений, отсутствующих в E24. [72]
| Код | Ряд | Цифра | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Письмо [№ 1] | Е24 | 9 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| А | 1.0 | 0,10 пФ | 1,0 пФ | 10 пФ | 100 пФ | 1,0 нФ | 10 нФ | 100 нФ | 1,0 мкФ | 10 мкФ | 100 мкФ |
| Б | 1.1 | 0,11 пФ | 1,1 пФ | 11 пФ | 110 пФ | 1,1 нФ | 11 нФ | 110 нФ | 1,1 мкФ | 11 мкФ | 110 мкФ |
| С | 1.2 | 0,12 пФ | 1,2 пФ | 12 пФ | 120 пФ | 1,2 нФ | 12 нФ | 120 нФ | 1,2 мкФ | 12 мкФ | 120 мкФ |
| Д | 1.3 | 0,13 пФ | 1,3 пФ | 13 пФ | 130 пФ | 1,3 нФ | 13 нФ | 130 нФ | 1,3 мкФ | 13 мкФ | 130 мкФ |
| Э | 1.5 | 0,15 пФ | 1,5 пФ | 15 пФ | 150 пФ | 1,5 нФ | 15 нФ | 150 нФ | 1,5 мкФ | 15 мкФ | 150 мкФ |
| Ф | 1.6 | 0,16 пФ | 1,6 пФ | 16 пФ | 160 пФ | 1,6 нФ | 16 нФ | 160 нФ | 1,6 мкФ | 16 мкФ | 160 мкФ |
| Г | 1.8 | 0,18 пФ | 1,8 пФ | 18 пФ | 180 пФ | 1,8 нФ | 18 нФ | 180 нФ | 1,8 мкФ | 18 мкФ | 180 мкФ |
| ЧАС | 2.0 | 0,20 пФ | 2,0 пФ | 20 пФ | 200 пФ | 2,0 нФ | 20 нФ | 200 нФ | 2,0 мкФ | 20 мкФ | 200 мкФ |
| Дж. | 2.2 | 0,22 пФ | 2,2 пФ | 22 пФ | 220 пФ | 2,2 нФ | 22 нФ | 220 нФ | 2,2 мкФ | 22 мкФ | 220 мкФ |
| К | 2.4 | 0,24 пФ | 2,4 пФ | 24 пФ | 240 пФ | 2,4 нФ | 24 нФ | 240 нФ | 2,4 мкФ | 24 мкФ | 240 мкФ |
| Л | 2.7 | 0,27 пФ | 2,7 пФ | 27 пФ | 270 пФ | 2,7 нФ | 27 нФ | 270 нФ | 2,7 мкФ | 27 мкФ | 270 мкФ |
| М | 3.0 | 0,30 пФ | 3,0 пФ | 30 пФ | 300 пФ | 3,0 нФ | 30 нФ | 300 нФ | 3,0 мкФ | 30 мкФ | 300 мкФ |
| Н | 3.3 | 0,33 пФ | 3,3 пФ | 33 пФ | 330 пФ | 3,3 нФ | 33 нФ | 330 нФ | 3,3 мкФ | 33 мкФ | 330 мкФ |
| П | 3.6 | 0,36 пФ | 3,6 пФ | 36 пФ | 360 пФ | 3,6 нФ | 36 нФ | 360 нФ | 3,6 мкФ | 36 мкФ | 360 мкФ |
| В | 3.9 | 0,39 пФ | 3,9 пФ | 39 пФ | 390 пФ | 3,9 нФ | 39 нФ | 390 нФ | 3,9 мкФ | 39 мкФ | 390 мкФ |
| Р | 4.3 | 0,43 пФ | 4,3 пФ | 43 пФ | 430 пФ | 4,3 нФ | 43 нФ | 430 нФ | 4,3 мкФ | 43 мкФ | 430 мкФ |
| С | 4.7 | 0,47 пФ | 4,7 пФ | 47 пФ | 470 пФ | 4,7 нФ | 47 нФ | 470 нФ | 4,7 мкФ | 47 мкФ | 470 мкФ |
| Т | 5.1 | 0,51 пФ | 5,1 пФ | 51 пФ | 510 пФ | 5,1 нФ | 51 нФ | 510 нФ | 5.1 мкФ | 51 мкФ | 510 мкФ |
| У | 5.6 | 0,56 пФ | 5,6 пФ | 56 пФ | 560 пФ | 5,6 нФ | 56 нФ | 560 нФ | 5,6 мкФ | 56 мкФ | 560 мкФ |
| В | 6.2 | 0,62 пФ | 6,2 пФ | 62 пФ | 620 пФ | 6,2 нФ | 62 нФ | 620 нФ | 6,2 мкФ | 62 мкФ | 620 мкФ |
| Вт | 6.8 | 0,68 пФ | 6,8 пФ | 68 пФ | 680 пФ | 6,8 нФ | 68 нФ | 680 нФ | 6,8 мкФ | 68 мкФ | 680 мкФ |
| Х | 7.5 | 0,75 пФ | 7,5 пФ | 75 пФ | 750 пФ | 7,5 нФ | 75 нФ | 750 нФ | 7,5 мкФ | 75 мкФ | 750 мкФ |
| И | 8.2 | 0,82 пФ | 8,2 пФ | 82 пФ | 820 пФ | 8,2 нФ | 82 нФ | 820 нФ | 8,2 мкФ | 82 мкФ | 820 мкФ |
| З | 9.1 | 0,91 пФ | 9,1 пФ | 91 пФ | 910 пФ | 9,1 нФ | 91 нФ | 910 нФ | 9,1 мкФ | 91 мкФ | 910 мкФ |
| Код | Ряд | Цифра | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Письмо | ОВОС | 9 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| а | 2.5 | 0,25 пФ | 2,5 пФ | 25 пФ | 250 пФ | 2,5 нФ | 25 нФ | 250 нФ | 2,5 мкФ | 25 мкФ | 250 мкФ |
| б? [73] | 3.0? [73] | 0,30 пФ | 3,0 пФ | 30 пФ | 300 пФ | 3,0 нФ | 30 нФ | 300 нФ | 3,0 мкФ | 30 мкФ | 300 мкФ |
| б? [72] /с? [73] | 3.5 | 0,35 пФ | 3,5 пФ | 35 пФ | 350 пФ | 3,5 нФ | 35 нФ | 350 нФ | 3,5 мкФ | 35 мкФ | 350 мкФ |
| г | 4.0 | 0,40 пФ | 4,0 пФ | 40 пФ | 400 пФ | 4,0 нФ | 40 нФ | 400 нФ | 4,0 мкФ | 40 мкФ | 400 мкФ |
| е | 4.5 | 0,45 пФ | 4,5 пФ | 45 пФ | 450 пФ | 4,5 нФ | 45 нФ | 450 нФ | 4,5 мкФ | 45 мкФ | 450 мкФ |
| ф | 5.0 | 0,50 пФ | 5,0 пФ | 50 пФ | 500 пФ | 5,0 нФ | 50 нФ | 500 нФ | 5,0 мкФ | 50 мкФ | 500 мкФ |
| м | 6.0 | 0,60 пФ | 6,0 пФ | 60 пФ | 600 пФ | 6,0 нФ | 60 нФ | 600 нФ | 6,0 мкФ | 60 мкФ | 600 мкФ |
| н | 7.0 | 0,70 пФ | 7,0 пФ | 70 пФ | 700 пФ | 7,0 нФ | 70 нФ | 700 нФ | 7,0 мкФ | 70 мкФ | 700 мкФ |
| т | 8.0 | 0,80 пФ | 8,0 пФ | 80 пФ | 800 пФ | 8,0 нФ | 80 нФ | 800 нФ | 8,0 мкФ | 80 мкФ | 800 мкФ |
| г | 9.0 | 0,90 пФ | 9,0 пФ | 90 пФ | 900 пФ | 9,0 нФ | 90 нФ | 900 нФ | 9,0 мкФ | 90 мкФ | 900 мкФ |
РКМ-код
Код RKM, соответствующий IEC 60062 и BS 1852, представляет собой обозначение для указания значения конденсатора на схеме цепи. Он избегает использования десятичного разделителя и заменяет десятичный разделитель префиксным символом SI для конкретного значения (и буквой F для веса 1). Код также используется для маркировки деталей. Например: 4n7 для 4,7 нФ или 2F2 для 2,2 Ф.
Исторический
В текстах до 1960-х годов и на некоторых корпусах конденсаторов до недавнего времени [17] устаревшие единицы измерения емкости использовались в электронных книгах, [74] журналах и каталогах электроники. [75] Старые единицы «мфд» и «мф» означали микрофарад (мкФ); а старые единицы «ммфд», «ммф», «мкф», «мкф», «пфд» означали пикофарад (пФ); но они редко используются в настоящее время. [76] Кроме того, «микромикрофарад» или «микро-микрофарад» — это устаревшие единицы, которые встречаются в некоторых старых текстах и эквивалентны пикофараду (пФ). [74]
Сводка устаревших единиц измерения емкости: (вариации верхнего/нижнего регистра не показаны)
- мкФ (микрофарад) = мф, мфд
- пФ (пикофарад) = ммф, ммфд, пфд, мкмкФ
Приложения

Хранение энергии
Конденсатор может хранить электрическую энергию, когда он отключен от своей зарядной цепи, поэтому его можно использовать как временную батарею или как другие типы перезаряжаемых систем хранения энергии . [77] Конденсаторы обычно используются в электронных устройствах для поддержания электропитания во время замены батарей. (Это предотвращает потерю информации в энергозависимой памяти.)
Конденсатор может способствовать преобразованию кинетической энергии заряженных частиц в электрическую энергию и хранить ее. [78]
Существуют компромиссы между конденсаторами и батареями как устройствами хранения. Без внешних резисторов или индукторов конденсаторы обычно могут высвобождать свою накопленную энергию за очень короткое время по сравнению с батареями. Наоборот, батареи могут удерживать гораздо больший заряд на свой размер. Обычные конденсаторы обеспечивают менее 360 джоулей на килограмм удельной энергии , тогда как обычная щелочная батарея имеет плотность 590 кДж/кг. Существует промежуточное решение: суперконденсаторы , которые могут принимать и отдавать заряд гораздо быстрее, чем батареи, и выдерживать гораздо больше циклов зарядки и разрядки, чем перезаряжаемые батареи. Однако они в 10 раз больше обычных батарей для данного заряда. С другой стороны, было показано, что количество заряда, хранящегося в диэлектрическом слое тонкопленочного конденсатора, может быть равно или даже превышать количество заряда, хранящегося на его пластинах. [79]
В автомобильных аудиосистемах большие конденсаторы хранят энергию для усилителя , чтобы использовать ее по требованию. Также, для импульсной лампы конденсатор используется для удержания высокого напряжения .
Цифровая память
В 1930-х годах Джон Атанасов применил принцип накопления энергии в конденсаторах для создания динамической цифровой памяти для первых двоичных компьютеров, которые использовали электронные лампы для логики. [80]
Импульсная энергия и оружие
Импульсная мощность используется во многих приложениях для увеличения интенсивности мощности (ватт) объема энергии (джоулей) путем высвобождения этого объема в течение очень короткого времени. Импульсы в диапазоне наносекунд и мощности в гигаватты достижимы. Короткие импульсы часто требуют специально сконструированных, низкоиндуктивных, высоковольтных конденсаторов, которые часто используются большими группами ( конденсаторные батареи ) для подачи огромных импульсов тока для многих приложений импульсной мощности. К ним относятся электромагнитное формирование , генераторы Маркса , импульсные лазеры (особенно TEA-лазеры ), сети формирования импульсов , радары , исследования термоядерного синтеза и ускорители частиц . [81]
Большие конденсаторные батареи (резервуары) используются в качестве источников энергии для взрывающихся мостовых детонаторов или ударных детонаторов в ядерном оружии и другом специализированном оружии. Ведутся экспериментальные работы по использованию батарей конденсаторов в качестве источников энергии для электромагнитной брони и электромагнитных рельсовых и койлганов .
Кондиционирование мощности

Накопительные конденсаторы используются в источниках питания , где они сглаживают выходной сигнал однополупериодного или однополупериодного выпрямителя . Они также могут использоваться в схемах подкачки заряда в качестве элемента накопления энергии при генерации более высоких напряжений, чем входное напряжение.
Конденсаторы подключаются параллельно к силовым цепям большинства электронных устройств и более крупных систем (например, заводов) для шунтирования и сокрытия колебаний тока от первичного источника питания, чтобы обеспечить «чистое» питание для сигнальных или управляющих цепей. Например, аудиооборудование использует несколько конденсаторов таким образом, чтобы шунтировать гул линии питания до того, как он попадет в сигнальную цепь. Конденсаторы действуют как локальный резерв для источника питания постоянного тока и обходят переменные токи от источника питания. Это используется в автомобильных аудиоприложениях, когда конденсатор жесткости компенсирует индуктивность и сопротивление выводов свинцово-кислотного автомобильного аккумулятора .
Коррекция коэффициента мощности

В распределении электроэнергии конденсаторы используются для коррекции коэффициента мощности . Такие конденсаторы часто поставляются в виде трех конденсаторов, соединенных как трехфазная нагрузка . Обычно значения этих конденсаторов указываются не в фарадах, а как реактивная мощность в вольт-амперах реактивных (вар). Цель состоит в том, чтобы противодействовать индуктивной нагрузке от таких устройств, как электродвигатели и линии электропередачи , чтобы нагрузка казалась в основном резистивной. Отдельные нагрузки двигателей или ламп могут иметь конденсаторы для коррекции коэффициента мощности, или более крупные наборы конденсаторов (обычно с автоматическими коммутационными устройствами) могут быть установлены в центре нагрузки внутри здания или на большой подстанции коммунальной сети .
Подавление и сопряжение
Сигнальная связь

Поскольку конденсаторы пропускают переменный ток, но блокируют сигналы постоянного тока (при зарядке до приложенного постоянного напряжения), их часто используют для разделения переменного и постоянного тока в сигнале. Этот метод известен как связь по переменному току или «емкостная связь». Здесь используется большое значение емкости, значение которой не нужно точно контролировать, но реактивное сопротивление которой мало на частоте сигнала.
Разъединение
Развязывающий конденсатор — это конденсатор, используемый для защиты одной части цепи от воздействия другой, например, для подавления шума или переходных процессов. Шум, вызванный другими элементами цепи, шунтируется через конденсатор, что снижает его воздействие на остальную часть цепи. Чаще всего он используется между источником питания и землей. Альтернативное название — обходной конденсатор , поскольку он используется для обхода источника питания или другого компонента цепи с высоким импедансом.
Разделительные конденсаторы не всегда должны быть дискретными компонентами. Конденсаторы, используемые в этих приложениях, могут быть встроены в печатную плату между различными слоями. Их часто называют встроенными конденсаторами. [82] Слои в плате, способствующие емкостным свойствам, также выполняют функции силовых и заземляющих плоскостей и имеют диэлектрик между собой, что позволяет им работать как параллельный плоский конденсатор.
Фильтры верхних и нижних частот
Подавление шума, скачки и демпферы
Когда индуктивная цепь размыкается, ток через индуктивность быстро исчезает, создавая большое напряжение в разомкнутой цепи переключателя или реле. Если индуктивность достаточно велика, энергия может генерировать искру, вызывая окисление, ухудшение или иногда сварку точек контакта или разрушение твердотельного переключателя. Демпфирующий конденсатор на вновь открытой цепи создает путь для этого импульса, чтобы обойти точки контакта, тем самым сохраняя их срок службы; они обычно встречаются в системах зажигания с контактным прерывателем , например. Аналогично, в схемах меньшего масштаба искра может быть недостаточной, чтобы повредить переключатель, но все равно может излучать нежелательные радиочастотные помехи (RFI), которые поглощает фильтрующий конденсатор . Демпфирующие конденсаторы обычно используются с резистором низкого номинала последовательно, чтобы рассеивать энергию и минимизировать RFI. Такие комбинации резистор-конденсатор доступны в одном корпусе.
Конденсаторы также используются параллельно с прерывательными блоками высоковольтного выключателя для равномерного распределения напряжения между этими блоками. Их называют «градуировочными конденсаторами».
На принципиальных схемах конденсатор, используемый в основном для хранения постоянного тока, часто изображается вертикально, при этом нижняя, более отрицательная пластина изображается в виде дуги. Прямая пластина указывает на положительный вывод устройства, если оно поляризовано (см. электролитический конденсатор ).
Пускатели двигателей
В однофазных двигателях с короткозамкнутым ротором первичная обмотка внутри корпуса двигателя не способна запустить вращательное движение ротора, но способна его поддерживать. Для запуска двигателя вторичная «пусковая» обмотка имеет последовательный неполяризованный пусковой конденсатор для введения свинца в синусоидальный ток. Когда вторичная (пусковая) обмотка расположена под углом по отношению к первичной (рабочей) обмотке, создается вращающееся электрическое поле. Сила вращающегося поля не постоянна, но достаточна для запуска вращения ротора. Когда ротор приближается к рабочей скорости, центробежный выключатель (или чувствительное к току реле последовательно с основной обмоткой) отключает конденсатор. Пусковой конденсатор обычно устанавливается сбоку корпуса двигателя. Их называют двигателями с конденсаторным пуском, которые имеют относительно высокий пусковой момент. Обычно они могут иметь до четырех раз больший пусковой момент, чем двигатель с расщепленной фазой, и используются в таких приложениях, как компрессоры, мойки высокого давления и любые небольшие устройства, требующие высокого пускового момента.
Асинхронные двигатели с конденсаторным управлением имеют постоянно подключенный фазосдвигающий конденсатор последовательно со второй обмоткой. Двигатель во многом похож на двухфазный асинхронный двигатель.
Пусковые конденсаторы двигателей обычно представляют собой неполяризованные электролитические конденсаторы, тогда как рабочие конденсаторы представляют собой обычные бумажные или пленочные диэлектрики.
Обработка сигнала
Энергия, хранящаяся в конденсаторе, может использоваться для представления информации , либо в двоичной форме, как в DRAM , либо в аналоговой форме, как в аналоговых выборочных фильтрах и ПЗС . Конденсаторы могут использоваться в аналоговых схемах в качестве компонентов интеграторов или более сложных фильтров, а также в стабилизирующих контурах отрицательной обратной связи . Схемы обработки сигналов также используют конденсаторы для интеграции токового сигнала.
Настроенные схемы
Конденсаторы и индукторы применяются вместе в настроенных схемах для выбора информации в определенных частотных диапазонах. Например, радиоприемники используют переменные конденсаторы для настройки частоты станции. Динамики используют пассивные аналоговые кроссоверы , а аналоговые эквалайзеры используют конденсаторы для выбора различных звуковых диапазонов.
Резонансная частота f настроенного контура является функцией последовательно соединенных индуктивности ( L ) и емкости ( C ) и определяется по формуле: где L измеряется в генри , а C — в фарадах.
Ощущение
Большинство конденсаторов разработаны для поддержания фиксированной физической структуры. Однако различные факторы могут изменить структуру конденсатора, и результирующее изменение емкости может быть использовано для обнаружения этих факторов.
- Изменение диэлектрика
- Эффекты изменения характеристик диэлектрика могут быть использованы для целей зондирования. Конденсаторы с открытым и пористым диэлектриком могут быть использованы для измерения влажности воздуха. Конденсаторы используются для точного измерения уровня топлива в самолетах ; по мере того, как топливо покрывает большую часть пары пластин, емкость цепи увеличивается. Сжатие диэлектрика может изменить конденсатор при давлении в несколько десятков бар достаточно, чтобы его можно было использовать в качестве датчика давления. [83] Выбранный, но в остальном стандартный полимерный диэлектрический конденсатор, будучи погруженным в совместимый газ или жидкость, может работать полезно как очень дешевый датчик давления до многих сотен бар.
- Изменение расстояния между пластинами
- Конденсаторы с гибкой пластиной могут использоваться для измерения деформации или давления. Промышленные датчики давления, используемые для управления процессами, используют мембраны, чувствительные к давлению, которые образуют конденсаторную пластину колебательного контура. Конденсаторы используются в качестве датчика в конденсаторных микрофонах , где одна пластина перемещается давлением воздуха относительно фиксированного положения другой пластины. Некоторые акселерометры используют MEMS- конденсаторы, вытравленные на чипе, для измерения величины и направления вектора ускорения. Они используются для обнаружения изменений ускорения, в датчиках наклона или для обнаружения свободного падения, в качестве датчиков, запускающих срабатывание подушек безопасности , и во многих других приложениях. Некоторые датчики отпечатков пальцев используют конденсаторы. Кроме того, пользователь может регулировать высоту тона музыкального инструмента терменвокс , перемещая руку, поскольку это изменяет эффективную емкость между рукой пользователя и антенной.
- Изменение эффективной площади пластин
- Емкостные сенсорные переключатели теперь [ когда? ] используются во многих потребительских электронных товарах.
Осцилляторы

Конденсатор может обладать пружинными свойствами в цепи генератора. В примере на изображении конденсатор влияет на напряжение смещения на базе npn-транзистора. Значения сопротивления резисторов делителя напряжения и значение емкости конденсатора вместе управляют частотой колебаний.
Производство света
Светоизлучающий конденсатор изготавливается из диэлектрика, который использует фосфоресценцию для получения света. Если одна из проводящих пластин сделана из прозрачного материала, свет виден. Светоизлучающие конденсаторы используются в конструкции электролюминесцентных панелей для таких применений, как подсветка ноутбуков. В этом случае вся панель представляет собой конденсатор, используемый для целей генерации света.
Опасности и безопасность
Опасности, создаваемые конденсатором, обычно определяются, прежде всего, количеством хранимой энергии, что является причиной таких вещей, как электрические ожоги или фибрилляция сердца . Такие факторы, как напряжение и материал корпуса, имеют второстепенное значение, они больше связаны с тем, насколько легко может быть инициирован удар, а не с тем, насколько большой ущерб может быть нанесен. [54] При определенных условиях, включая проводимость поверхностей, существующие медицинские состояния, влажность воздуха или пути, по которым он проходит через тело (то есть: удары, проходящие через ядро тела и, особенно, через сердце, более опасны, чем те, которые ограничены конечностями), сообщалось, что удары силой всего в один джоуль вызывают смерть, хотя в большинстве случаев они могут даже не оставлять ожогов. Удары силой более десяти джоулей, как правило, повреждают кожу и обычно считаются опасными. Любой конденсатор, который может хранить 50 джоулей или более, следует считать потенциально смертельным. [84] [54]
Конденсаторы могут сохранять заряд в течение длительного времени после отключения питания от цепи; этот заряд может вызвать опасные или даже потенциально смертельные удары током или повредить подключенное оборудование. Например, даже такое, казалось бы, безобидное устройство, как вспышка одноразовой камеры , имеет конденсатор фотовспышки , который может содержать более 15 джоулей энергии и быть заряженным до более чем 300 вольт. Это легко может вызвать удар током. Процедуры обслуживания электронных устройств обычно включают инструкции по разрядке больших или высоковольтных конденсаторов, например, с помощью палочки Бринкли . Большие конденсаторы, такие как те, которые используются в микроволновых печах , блоках HVAC и медицинских дефибрилляторах, также могут иметь встроенные разрядные резисторы для рассеивания накопленной энергии до безопасного уровня в течение нескольких секунд после отключения питания. Высоковольтные конденсаторы хранятся с закороченными клеммами , в качестве защиты от потенциально опасных напряжений из-за диэлектрической абсорбции или от переходных напряжений, которые конденсатор может получить от статических зарядов или проходящих погодных явлений. [54]
Некоторые старые большие масляные бумажные или пленочные конденсаторы содержат полихлорированные бифенилы (ПХБ). Известно, что отходы ПХБ могут просачиваться в грунтовые воды под свалками . Конденсаторы, содержащие ПХБ, были маркированы как содержащие «Аскарель» и несколько других торговых наименований. Бумажные конденсаторы, заполненные ПХБ, встречаются в очень старых (до 1975 года) балластах люминесцентных ламп и других устройствах.
Конденсаторы могут катастрофически выйти из строя, если подвергнуть их напряжению или току, превышающему их номинал, или в случае поляризованных конденсаторов, примененных в обратной полярности. Неисправности могут привести к образованию дуги, которая нагревает и испаряет диэлектрическую жидкость, вызывая накопление сжатого газа, что может привести к вздутию, разрыву или взрыву. Более крупные конденсаторы могут иметь вентиляционные отверстия или аналогичный механизм, позволяющий сбрасывать такое давление в случае отказа. Конденсаторы, используемые в радиочастотных или длительно сильных токах, могут перегреваться, особенно в центре рулонов конденсаторов. Конденсаторы, используемые в высокоэнергетических конденсаторных батареях, могут сильно взорваться, когда короткое замыкание в одном конденсаторе вызывает внезапный сброс энергии, накопленной в остальной части батареи, в неисправный блок. Высоковольтные вакуумные конденсаторы могут генерировать мягкое рентгеновское излучение даже во время нормальной работы. Надлежащая локализация, плавление и профилактическое обслуживание могут помочь свести эти опасности к минимуму.
Высоковольтные конденсаторы могут выиграть от предварительной зарядки для ограничения пусковых токов при включении питания цепей постоянного тока высокого напряжения (HVDC). Это продлевает срок службы компонента и может смягчить опасности высокого напряжения.
- Разбухшие электролитические конденсаторы. Отверстие наверху позволяет выпустить сжатый газ, скопившийся в случае отказа, предотвращая взрыв.
- Этот высокоэнергетический конденсатор дефибриллятора имеет резистор, подключенный между клеммами в целях безопасности для рассеивания накопленной энергии.
- Взорвавшийся электролитический конденсатор, видны фрагменты бумаги и металлической фольги.
Смотрите также
- Измеритель емкости
- Конденсаторная чума
- Электрическое поле смещения
- Электролюминесценция
- Список производителей конденсаторов
Примечания
- ^ Большинство реальных конденсаторов могут иметь небольшой ток утечки диэлектрика, который проходит через резистивный диэлектрический слой между пластинами.
- ^ Чтобы снизить риск ошибок чтения, буквы
IиOне используются, поскольку их глифы похожи на другие буквы и цифры.
Ссылки
- ^ ab Duff, Wilmer (1916) [1908]. Учебник физики (4-е изд.). Филадельфия: P. Blakiston's Son & Co. стр. 361. Получено 01.12.2016 .
- ^ Bird, John (2010). Электрические и электронные принципы и технологии. Routledge. С. 63–76. ISBN 978-0-08089056-2. Получено 17.03.2013 .
- ^ Флойд, Томас (2005) [1984]. Электронные приборы (7-е изд.). Верхняя Сэддл-Ривер, Нью-Джерси, США: Pearson Education . стр. 10. ISBN 0-13-127827-4.
- ^ «Молекулярные выражения: электричество и магнетизм — интерактивные учебные пособия по Java: Молния: естественный конденсатор». micro.magnet.fsu.edu .
- ^ Уильямс, Генри Смит. "История науки. Том II, часть VI: Лейденская банка обнаружена". Архивировано из оригинала 2007-10-24 . Получено 2013-03-17 .
- ^ Кейтли, Джозеф Ф. (1999). История электрических и магнитных измерений: с 500 г. до н. э. до 1940-х гг. John Wiley & Sons. стр. 23. ISBN 978-0780311930. Получено 17.03.2013 .
- ^ Хьюстон, Эдвин Дж. (1905). Электричество в повседневной жизни. PF Collier & Son. стр. 71. Получено 17.03.2013 .
- ^ Бенджамин, Парк (1895). История электричества: (Интеллектуальный рост электричества) от античности до дней Бенджамина Франклина. J. Wiley & Sons . С. 522–524.
- ^ Айзексон, Уолтер (2003). Бенджамин Франклин: Американская жизнь. Саймон и Шустер. стр. 136. ISBN 978-0-74326084-8. Получено 17.03.2013 .
- ^ Франклин, Бенджамин (1749-04-29). "Эксперименты и наблюдения над электричеством: Письмо IV Питеру Коллинсону" (PDF) . стр. 28 . Получено 2009-08-09 .
- ^ Морзе, Роберт А. (сентябрь 2004 г.). «Франклин и электростатика – Бен Франклин как мой лабораторный партнер» (PDF) . Центр научного образования Райта . Университет Тафтса. стр. 23 . Получено 10 августа 2009 г. .
После открытия Вольтой электрохимической ячейки в 1800 г. этот термин стал применяться к группе электрохимических ячеек
- ^ Вольф, А.; Макки, Д. (1962). История науки, техники и философии в XVIII веке (2-е изд.). Лондон: Джордж Аллен и Анвин. С. 224.
- ^ "eFunda: Глоссарий: Единицы: Электрическая емкость: Банка". eFunda . Получено 2013-03-17 .
- ^ Панкальди, Г. (2003). Вольта: Наука и культура в эпоху Просвещения . Принстон: Princeton University Press. стр. 112–126. ISBN 0691096856.
- ^ "Очерк Алессандро Вольта". The Popular Science Monthly . Нью-Йорк: Bonnier Corporation: 118–119. Май 1892. ISSN 0161-7370.
- ^ Британская ассоциация инженерных стандартов, Британский стандартный словарь терминов по электротехнике , C. Lockwood & Son, 1926
- ^ abcdef Хо, Джанет; Джоу, Т. Ричард; Боггс, Стивен (январь 2010 г.). «Историческое введение в технологию конденсаторов». Журнал IEEE Electrical Insulation . 26 (1): 20–25. doi :10.1109/mei.2010.5383924. S2CID 23077215.
- ↑ US 2800616, Becker, HI, "Низковольтный электролитический конденсатор", выдан 23 июля 1957 г.
- ^ Краткая история суперконденсаторов ОСЕНЬ 2007 г. Батареи и технологии хранения энергии Архивировано 06.01.2014 на Wayback Machine
- ^ Sze, Simon Min ; Lee, Ming-Kwei (май 2012). "MOS Capacitor and MOSFET". Полупроводниковые приборы: физика и технология. John Wiley & Sons . ISBN 978-0-47053794-7. Получено 2019-10-06 .
- ^ "DRAM". IBM100 . IBM . 2017-08-09 . Получено 2019-09-20 .
- ^ Sze, Simon M. (2002). Полупроводниковые приборы: физика и технология (PDF) (2-е изд.). Wiley . стр. 214. ISBN 0-471-33372-7. Архивировано из оригинала (PDF) 2023-01-23.
- ^ ab Ulaby 1999, стр. 168.
- ^ Улаби 1999, стр. 157.
- ^ Улаби 1999, стр. 69.
- ^ Пиллаи, КП (1970). «Окраинное поле конечных параллельных плоских конденсаторов». Труды Института инженеров-электриков . 117 (6): 1201–1204. doi :10.1049/piee.1970.0232.
- ^ ab Purcell, Edward (2011). Электричество и магнетизм, 2-е изд. Cambridge University Press . стр. 110–111. ISBN 978-1-13950355-6.
- ^ ab Serway, Raymond A.; Vuille, Chris (2014). College Physics, 10-е изд. Cengage Learning. стр. 582. ISBN 978-1-30514282-4.
- ^ Хаммонд, П. (2013). Электромагнетизм для инженеров: вводный курс. Elsevier Science. стр. 44–45. ISBN 978-1-48314978-3.
- ^ Дорф и Свобода 2001, стр. 263.
- ^ Дорф и Свобода 2001, стр. 260.
- ^ "Зарядка и разрядка конденсатора". Все о схемах . Получено 2009-02-19 .
- ^ Протекание тока через резисторы и конденсаторы PLoS one 2017
- ^ "(PDF) Универсальность эмерджентного масштабирования в конечных случайных бинарных перколяционных сетях".
- ^ Улаби 1999, стр. 170.
- ^ Pai, ST; Zhang, Qi (1995). Введение в технологию импульсов высокой мощности. Расширенная серия по электротехнике и вычислительной технике. Том 10. World Scientific. ISBN 978-9810217143. Получено 17.03.2013 .
- ^ Дайер, Стивен А. (2004). Обзор приборов и измерений Wiley. John Wiley & Sons . стр. 397. ISBN 978-0-47122165-4. Получено 17.03.2013 .
- ^ Шерц, Пол (2006). Практическая электроника для изобретателей (2-е изд.). McGraw Hill Professional . стр. 100. ISBN 978-0-07177644-8. Получено 17.03.2013 .
- ^ Инуиши, Y.; Пауэрс, DA (1957). «Электрический пробой и проводимость через майларовые пленки». Журнал прикладной физики . 28 (9): 1017–1022. Bibcode : 1957JAP....28.1017I. doi : 10.1063/1.1722899.
- ^ Рид, CW; Чихановски, SW (1994). «Основы старения высоковольтных полимерно-пленочных конденсаторов». Труды IEEE по диэлектрикам и электроизоляции . 1 (5): 904–922. doi :10.1109/94.326658.
- ^ Кляйн, Н.; Гафни, Х. (1966). «Максимальная диэлектрическая прочность тонких пленок оксида кремния». Труды IEEE по электронным приборам . 13 (2): 281–289. Bibcode : 1966ITED...13..281K. doi : 10.1109/T-ED.1966.15681.
- ^ Белкин, А.; и др. (2017). «Восстановление наноконденсаторов из оксида алюминия после высоковольтного пробоя». Scientific Reports . 7 (1): 932. Bibcode :2017NatSR...7..932B. doi :10.1038/s41598-017-01007-9. PMC 5430567 . PMID 28428625.
- ^ Bird, John (2007). Теория и технология электрических цепей. Routledge. стр. 501. ISBN 978-0-75068139-1. Получено 17.03.2013 .
- ^ Bisquert, J.; Garcia-Belmonte, G.; Fabregat-Santiago, F. (2000). «Роль приборов в процессе моделирования реальных конденсаторов». IEEE Transactions on Education . 43 (4): 439–442. Bibcode : 2000ITEdu..43..439F. doi : 10.1109/13.883355. ISSN 1557-9638.
- ^ Улаби 1999, стр. 169.
- ^ "Ceramic Capacitor Aging Made Simple". Johanson Dielectrics. 2012-05-21. Архивировано из оригинала 2012-12-26 . Получено 2013-03-17 .
- ^ "Краткое руководство по типам конденсаторов". EETech Media LLC . Получено 2023-09-07 .
- ^ "Влияние реверсирования на срок службы конденсатора" (PDF) . Engineering Bulletin 96-004 . Sorrento Electronics. Ноябрь 2003 г. Архивировано из оригинала (PDF) 2014-07-14 . Получено 2013-03-17 .
- ^ Kaiser, Cletus J. (2012-12-06). Справочник по конденсаторам. Springer Science & Business Media. ISBN 978-9-40118090-0.
- ^ Электроника . McGraw-Hill 1960 стр. 90
- ^ Советы по безопасности при использовании ксеноновых стробоскопов и вспышек. donklipstein.com. 2006-05-29
- ^ Prutchi, David (2012). Исследование квантовой физики с помощью практических проектов. John Wiley & Sons . стр. 10. ISBN 978-1-11817070-0.
- ^ Диксит, Дж. Б.; Ядав, Амит (2010). Качество электроэнергии. Laxmi Publications, Ltd. стр. 63. ISBN 978-9-38038674-4.
- ^ abcd Winburn (1989). Практическая лазерная безопасность, второе издание. CRC Press . стр. 189. ISBN 978-0-82478240-5.
- ↑ «Руководство Робинсона по радиотелеграфии и телефонии» С.С. Робинсона — Военно-морской институт США, 1924 г., стр. 170.
- ^ Гупта, Анунай; Ядав, Ом Пракаш; ДеВото, Дуглас; Мейджор, Джошуа (октябрь 2018 г.). «Обзор поведения при деградации и моделирование конденсаторов» (PDF) . Национальная лаборатория возобновляемой энергии. Архивировано (PDF) из оригинала 2020-06-05 . Получено 2021-07-23 .
- ^ Гинта, Стив. «Спросите инженера по приложениям – 21». Analog Devices . Получено 17.03.2013 .
- ^ de Araujo, Carlos Paz; Ramesh, Ramamoorthy; Taylor, George W., ред. (2001). Science and Technology of Integrated Ferroelectrics: Selected Papers from Eleven Years of the Proceedings of the International Symposium on Integrated Ferroelectrics. CRC Press . Рисунок 2, стр. 504. ISBN 90-5699-704-1.
- ^ Musikant, Solomon (1991). Что каждый инженер должен знать о керамике. CRC Press . Рисунок 3.9, стр. 43. ISBN 0-8247-8498-7.
- ^ Ясуо Чо (2005). Сканирующий нелинейный диэлектрический микроскоп (в полярных оксидах ; Р. Васер , У. Беттгер и С. Тидке, редакторы). Wiley-VCH. Глава 16. ISBN 3-527-40532-1.
- ^ ab Sze & Ng 2006, стр. 217.
- ^ Джулиани, Габриэле; Виньяле, Джованни (2005). Квантовая теория электронной жидкости. Издательство Кембриджского университета . п. 111. ИСБН 0-521-82112-6.
- ^ Раммер, Йорген (2007). Квантовая теория поля неравновесных состояний. Cambridge University Press . стр. 158. ISBN 978-0-52187499-1.
- ^ Czichos, Horst; Saito, Tetsuya; Smith, Leslie (2006). Springer Handbook of Materials Measurement Methods. Springer. стр. 475. ISBN 3-540-20785-6.
- ^ Коффи, Уильям; Калмыков, Ю. П. (2006). Фракталы, диффузия и релаксация в неупорядоченных сложных системах. Часть A. Wiley. стр. 17. ISBN 0-470-04607-4.
- ↑ Конференция IEEE по измерительным и инструментальным технологиям (IMTC) 2005 г.: Оттава, Онтарио, Канада, 16–19 мая 2005 г. IEEE. 2005. стр. 1350–1353. doi :10.1109/IMTC.2005.1604368. ISBN 978-0-78038879-6. S2CID 37739028.
- ^ Шредер 2006, стр. 347.
- ^ Шредер 2006, стр. 305.
- ^ Касап, Сафа О.; Каппер, Питер (2006). Springer Handbook of Electronic and Photonic Materials. Springer. Рисунок 20.22, стр. 425.
- ^ PY Yu; Cardona, Manuel (2001). Основы полупроводников (3-е изд.). Springer. §6.6 "Модуляционная спектроскопия". ISBN 3-540-25470-6.
- ^ Каплан, Дэниел М.; Уайт, Кристофер Г. (2003). Hands-On Electronics: A Practical Introduction to Analog and Digital Circuits. Cambridge University Press . стр. 19. ISBN 978-0-52189351-0.
- ^ ab "Приложение B: Специальная двухсимвольная система кодирования для конденсаторов". SLOVENSKI STANDARD SIST EN 60062:2016/A1:2019 (PDF) (предварительный просмотр). 2019-12-01. стр. 3–4. Архивировано (PDF) из оригинала 2022-06-17 . Получено 2022-06-17 .
- ^ abc Забкар, Франк (2011-09-15). "EIA-198-D capacitance codes". Архивировано из оригинала 2022-06-17 . Получено 2022-06-18 .
- ^ ab «Основы электроники, том 1b: Основы электричества, переменный ток, NAVPERS 93400A-1b». 1965-04-12 – через интернет-архив.
- ^ "Каталог 1930 г. – Конденсаторы (конденсаторы)". Allied Radio . стр. 139. Архивировано из оригинала 2017-07-11 . Получено 2017-07-11 .
- ^ "Таблица преобразования конденсатора MF - MMFD". www.justradios.com .
- ^ Миллер, Чарльз (2011). Иллюстрированное руководство по Национальному электротехническому кодексу. Cengage Learning. стр. 445.
- ^ Шинн, Эрик и др. (2012). «Преобразование ядерной энергии с помощью стопок графеновых наноконденсаторов». Сложность . 18 (3): 24–27. Bibcode : 2013Cmplx..18c..24S. doi : 10.1002/cplx.21427.
- ^ Безрядин, А.; Белкин, А.; и др. (2017). "Большая эффективность хранения энергии диэлектрического слоя графеновых наноконденсаторов". Нанотехнологии . 28 (49): 495401. arXiv : 2011.11867 . Bibcode : 2017Nanot..28W5401B. doi : 10.1088/1361-6528/aa935c. PMID 29027908. S2CID 44693636.
- ^ Флойд, Томас Л. (2017). Электронные устройства. Pearson. стр. 10. ISBN 978-0-13441444-7.
- ^ Импульсная мощность Геннадия А. Месяца -- Springer 2005 Страница 1--5
- ^ Алам, Мохаммед; Азарян, Майкл Х.; Остерман, Майкл; Пехт, Майкл (2010). «Эффективность встроенных конденсаторов в снижении количества конденсаторов поверхностного монтажа для развязывающих приложений». Circuit World . 36 (1): 22. doi :10.1108/03056121011015068.
- ^ Дауни, Нил А. и Матильда Прадье, «Метод и устройство для контроля давления жидкости», патент США 7526961 (2009)
- ^ "Некоторые советы по безопасности при использовании ксеноновых стробоскопов и вспышек". donklipstein.com .
Библиография
- Дорф, Ричард К.; Свобода, Джеймс А. (2001). Введение в электрические цепи (5-е изд.). Нью-Йорк: John Wiley & Sons. ISBN 978-0-47138689-6.
- Философские труды Королевского общества LXXII, Приложение 8, 1782 г. (Вольта придумал слово « конденсатор »)
- Ulaby, Fawwaz Tayssir (1999). Основы прикладной электродинамики (2-е изд.). Upper Saddle River, Нью-Джерси, США: Prentice Hall . ISBN 978-0-13011554-6.
- Шредер, Дитер К. (2006). Характеристика полупроводниковых материалов и приборов (3-е изд.). Wiley. стр. 270 и далее . ISBN 978-0-47173906-7.
- Sze, Simon M.; Ng, Kwok K. (2006). Физика полупроводниковых приборов (3-е изд.). Wiley. ISBN 978-0-47006830-4.
Дальнейшее чтение
- Конденсаторы на основе тантала и ниобия – наука, технология и применение ; 1-е изд.; Юрий Фримен; Springer; 120 страниц; 2018; ISBN 978-3-31967869-6 .
- Конденсаторы ; 1-е изд.; RP Deshpande; McGraw-Hill; 342 страницы; 2014; ISBN 978-0-07184856-5 .
- Справочник по конденсаторам ; 1-е изд.; Клетус Кайзер; Ван Ностранд Рейнхольд; 124 страницы; 1993; ISBN 978-9-40118092-4 .
- Понимание конденсаторов и их применения ; 1-е изд.; Уильям Маллин; Sams Publishing; 96 страниц; 1964. (архив)
- Постоянные и переменные конденсаторы ; 1-е изд.; GWA Dummer и Harold Nordenberg; Maple Press; 288 страниц; 1960. (архив)
- Электролитический конденсатор ; 1-е изд.; Александр Георгиев; Murray Hill Books; 191 стр.; 1945. (архив)
Внешние ссылки
- Первый конденсатор – пивной бокал – SparkMuseum
- Как работают конденсаторы – Howstuffworks
- Учебное пособие по конденсаторам











































































![{\displaystyle dW=Q\,dV=\left[\int _{0}^{V}dV'\,C(V')\right]dV\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d6cbac71e27b7dd2c7c9156f89df76670526292c)



![{\displaystyle {\begin{aligned}I(\omega )&=j\omega Q(\omega )=j\omega \oint _{\Sigma }{\boldsymbol {D}}({\boldsymbol {r}},\omega )\cdot d{\boldsymbol {\Sigma }}\\&=\left[G(\omega )+j\omega C(\omega )\right]V(\omega )={\frac {V(\omega )}{Z(\omega )}}\,,\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/654a10c670f2fa6bc1763d52f2159161362b5fcb)








