эффект Зеемана

Эффект Зеемана ( / ˈ z eɪ m ə n / ZAY -mən , голландский : [ˈzeːmɑn] ) — это расщепление спектральной линии на несколько компонент в присутствии статического магнитного поля . Он вызван взаимодействием магнитного поля с магнитным моментом атомного электрона , связанным с его орбитальным движением и спином ; это взаимодействие сдвигает некоторые орбитальные энергии больше, чем другие, что приводит к расщеплению спектра. Эффект назван в честь голландского физика Питера Зеемана , который открыл его в 1896 году и получил Нобелевскую премию по физике за это открытие. Он аналогичен эффекту Штарка , расщеплению спектральной линии на несколько компонент в присутствии электрического поля . Также подобно эффекту Штарка, переходы между различными компонентами имеют, как правило, разную интенсивность, причем некоторые полностью запрещены (в дипольном приближении), как это регулируется правилами отбора .

Поскольку расстояние между подуровнями Зеемана является функцией напряженности магнитного поля, этот эффект можно использовать для измерения напряженности магнитного поля, например, Солнца и других звезд или в лабораторной плазме .

В 1896 году Зееман узнал, что в его лаборатории имеется одна из самых высокоразрешающих дифракционных решеток Генри Августа Роуленда . Зееман прочитал статью Джеймса Клерка Максвелла в Encyclopaedia Britannica, описывающую неудачные попытки Майкла Фарадея повлиять на свет с помощью магнетизма. Зееман задавался вопросом, смогут ли новые спектрографические методы добиться успеха там, где ранние попытки не увенчались успехом. ^{[1] : 75}

При освещении щелевидным источником решетка создает длинный массив щелевых изображений, соответствующих разным длинам волн. Зееман поместил кусок асбеста, пропитанный соленой водой, в пламя горелки Бунзена у источника решетки: он мог легко увидеть две линии для излучения натрия . Приведя в действие магнит в 10 килогаусс вокруг пламени, он наблюдал небольшое расширение изображений натрия. ^{[1] : 76}

Когда Зееман переключился на кадмий в качестве источника, он наблюдал, как изображения расщеплялись, когда магнит был заряжен. Эти расщепления можно было проанализировать с помощью новой тогда электронной теории Хендрика Лоренца . Оглядываясь назад, мы теперь знаем, что магнитные эффекты на натрии требуют квантово-механической обработки. ^{[1] : 77} Зееман и Лоренц были награждены Нобелевской премией 1902 года; в своей благодарственной речи Зееман объяснил свой аппарат и показал слайды спектрографических изображений. ^[2]

Исторически различают нормальный и аномальный эффект Зеемана (открытый Томасом Престоном в Дублине, Ирландия ^[3] ). Аномальный эффект появляется при переходах, где суммарный спин электронов не равен нулю. Он был назван «аномальным», потому что спин электрона еще не был открыт, и поэтому не было хорошего объяснения для него в то время, когда Зееман наблюдал эффект. Вольфганг Паули вспоминал, что когда его коллега спросил его, почему он выглядит несчастным, он ответил: «Как человек может выглядеть счастливым, когда он думает об аномальном эффекте Зеемана?» ^[4]

При более высокой напряженности магнитного поля эффект перестает быть линейным. При еще более высокой напряженности поля, сравнимой с напряженностью внутреннего поля атома, нарушается электронная связь и спектральные линии перестраиваются. Это называется эффектом Пашена–Бака.

В современной научной литературе эти термины используются редко, с тенденцией использовать просто «эффект Зеемана». Другой редко используемый малоизвестный термин — обратный эффект Зеемана , ^[5] относящийся к эффекту Зеемана в спектральной линии поглощения.

Похожий эффект, расщепление уровней ядерной энергии в присутствии магнитного поля, называется ядерным эффектом Зеемана . ^[6]

Полный гамильтониан атома в магнитном поле равен

${\displaystyle H=H_{0}+V_{\rm {M}},\ }$

где — невозмущенный гамильтониан атома, а — возмущение, вызванное магнитным полем:${\displaystyle H_{0}}$${\displaystyle V_{\rm {M}}}$

${\displaystyle V_{\rm {M}}=- {\vec {\mu }}\cdot {\vec {B}},}$

где - магнитный момент атома. Магнитный момент состоит из электронной и ядерной частей; однако последняя на много порядков меньше и здесь будет учитываться. Поэтому,${\displaystyle {\vec {\mu }}}$

${\displaystyle {\vec {\mu }}\approx - {\frac {\mu _ {\rm {B}}g {\vec {J}}}{\hbar }},}$

где — магнетон Бора , — полный электронный угловой момент , а — g-фактор Ланде . Более точный подход заключается в том, чтобы учесть, что оператор магнитного момента электрона представляет собой сумму вкладов орбитального углового момента и спинового углового момента , каждый из которых умножен на соответствующее гиромагнитное отношение :${\displaystyle \mu _ {\rm {B}}}$${\displaystyle {\vec {J}}}$${\displaystyle г}$ ${\displaystyle {\vec {L}}}$ ${\displaystyle {\vec {S}}}$

${\displaystyle {\vec {\mu }}=- {\frac {\mu _{\rm {B}}(g_{l}{\vec {L}}+g_{s}{\vec {S}})}{\hbar }},}$

где и (последнее называется аномальным гиромагнитным отношением ; отклонение значения от 2 обусловлено эффектами квантовой электродинамики ). В случае LS-связи можно просуммировать по всем электронам в атоме:${\displaystyle g_{l}=1}$${\displaystyle g_{s}\приблизительно 2,0023193}$

${\displaystyle g{\vec {J}}=\left\langle \sum _{i}(g_{l}{\vec {l_{i}}}+g_{s}{\vec {s_{i}}})\right\rangle =\left\langle (g_{l}{\vec {L}}+g_{s}{\vec {S}})\right\rangle ,}$

где и — полный спиновый момент и спин атома, а усреднение производится по состоянию с заданным значением полного углового момента.${\displaystyle {\vec {L}}}$${\displaystyle {\vec {S}}}$

Если член взаимодействия мал (меньше тонкой структуры ), его можно рассматривать как возмущение; это собственно эффект Зеемана. В эффекте Пашена-Бака, описанном ниже, значительно превышает связь LS (но все еще мало по сравнению с ). В сверхсильных магнитных полях взаимодействие магнитного поля может превышать , в этом случае атом больше не может существовать в своем обычном значении, и вместо этого говорят об уровнях Ландау . Существуют промежуточные случаи, которые сложнее этих предельных случаев.${\displaystyle V_{M}}$${\displaystyle V_{M}}$${\displaystyle H_{0}}$${\displaystyle H_{0}}$

Если спин-орбитальное взаимодействие доминирует над эффектом внешнего магнитного поля и не сохраняется отдельно, сохраняется только полный угловой момент. Векторы спина и орбитального углового момента можно рассматривать как прецессирующие вокруг (фиксированного) вектора полного углового момента . Тогда (временно)-"усредненный" вектор спина является проекцией спина на направление :${\displaystyle {\vec {L}}}$${\displaystyle {\vec {S}}}$${\displaystyle {\vec {J}}={\vec {L}}+{\vec {S}}}$${\displaystyle {\vec {J}}}$${\displaystyle {\vec {J}}}$

${\displaystyle {\vec {S}}_{\rm {avg}}={\frac {({\vec {S}}\cdot {\vec {J}})}{J^{2}}}{\vec {J}}}$

и для (временного) «усредненного» орбитального вектора:

${\displaystyle {\vec {L}}_{\rm {avg}}={\frac {({\vec {L}}\cdot {\vec {J}})}{J^{2}}}{\vec {J}}.}$

Таким образом,

${\displaystyle \langle V_{\rm {M}}\rangle = {\frac {\mu _ {\rm {B}}}{\hbar }}{\vec {J}} \left(g_ {L}{\frac {{\vec {L}}\cdot {\vec {J}}}{J^{2}}}+g_ {S}{\frac {{\vec {S}} \cdot {\vec {J}}}{J^{2}}}\right)\cdot {\vec {B}}.}$

Используя и возводя в квадрат обе части, получаем${\displaystyle {\vec {L}}={\vec {J}}-{\vec {S}}}$

${\displaystyle {\vec {S}}\cdot {\vec {J}}={\frac {1}{2}}(J^{2}+S^{2}-L^{2})={\frac {\hbar ^{2}}{2}}[j(j+1)-l(l+1)+s(s+1)],}$

и: используя и возводя в квадрат обе части, получаем${\displaystyle {\vec {S}}={\vec {J}}-{\vec {L}}}$

${\displaystyle {\vec {L}}\cdot {\vec {J}}={\frac {1}{2}}(J^{2}-S^{2}+L^{2})={\frac {\hbar ^{2}}{2}}[j(j+1)+l(l+1)-s(s+1)].}$

Объединяя все и принимая , получаем магнитную потенциальную энергию атома в приложенном внешнем магнитном поле,${\displaystyle J_{z}=\hbar m_{j}}$

${\displaystyle {\begin{aligned}V_{\rm {M}}&=\mu _{\rm {B}}Bm_{j}\left[g_{L}{\frac {j(j+1)+l(l+1)-s(s+1)}{2j(j+1)}}+g_{S}{\frac {j(j+1)-l(l+1)+s(s+1)}{2j(j+1)}}\right]\\&=\mu _{\rm {B}}Bm_{j}\left[1+(g_{S}-1){\frac {j(j+1)-l(l+1)+s(s+1)}{2j(j+1)}}\right],\\&=\mu _{\rm {B}}Bm_{j}g_{j}\end{aligned}}}$

где величина в квадратных скобках — это g-фактор Ланде g _J атома ( и ), а — z-компонента полного углового момента. Для одного электрона над заполненными оболочками и g-фактор Ланде можно упростить до:${\displaystyle g_{L}=1}$${\displaystyle g_{S}\approx 2}$${\displaystyle m_{j}}$${\displaystyle s=1/2}$${\displaystyle j=l\pm s}$

${\displaystyle g_{j}=1\pm {\frac {g_{S}-1}{2l+1}}}$

Принимая в качестве возмущения поправку Зеемана к энергии, получим${\displaystyle V_{m}}$

${\displaystyle {\begin{aligned}E_{\rm {Z}}^{(1)}=\langle nljm_{j}|H_{\rm {Z}}^{'}|nljm_{j}\rangle =\langle V_{M}\rangle _{\Psi }=\mu _{\rm {B}}g_{J}B_{\rm {ext}}m_{j}\end{aligned}}}$

Переход Лайман -альфа в водороде при наличии спин-орбитального взаимодействия включает переходы

${\displaystyle 2P_{1/2}\to 1S_{1/2}}$и${\displaystyle 2P_{3/2}\to 1S_{1/2}.}$

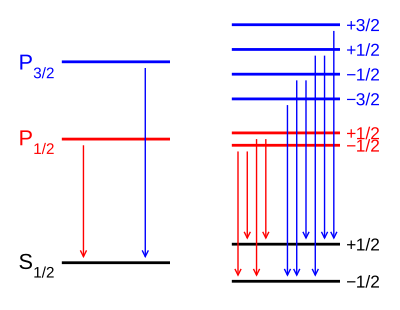
При наличии внешнего магнитного поля эффект Зеемана в слабом поле расщепляет уровни 1S _1/2 и 2P _1/2 на 2 состояния каждый ( ), а уровень 2P _3/2 — на 4 состояния ( ). G-факторы Ланде для трех уровней равны:${\displaystyle m_{j}=1/2,-1/2}$${\displaystyle m_{j}=3/2,1/2,-1/2,-3/2}$

${\displaystyle g_{J}=2}$для (j=1/2, l=0)${\displaystyle 1S_{1/2}}$

${\displaystyle g_{J}=2/3}$для (j=1/2, l=1)${\displaystyle 2P_{1/2}}$

${\displaystyle g_{J}=4/3}$для (j=3/2, l=1).${\displaystyle 2P_{3/2}}$

Обратите внимание, что размер расщепления энергии различен для разных орбиталей, поскольку значения g _J различны. Слева изображено тонкоструктурное расщепление. Это расщепление происходит даже при отсутствии магнитного поля, поскольку оно обусловлено спин-орбитальной связью. Справа изображено дополнительное зеемановское расщепление, которое происходит при наличии магнитных полей.

Дипольно-разрешенные переходы Лайман-альфа в режиме слабого поля

Начальное состояние ( )${\displaystyle n=2,l=1}$ ${\displaystyle \mid j,m_{j}\rangle }$	Конечное состояние ( )${\displaystyle n=1,l=0}$ ${\displaystyle \mid j,m_{j}\rangle }$	Возмущение энергии
${\displaystyle \left|{\frac {1}{2}},\pm {\frac {1}{2}}\right\rangle }$	${\displaystyle \left|{\frac {1}{2}},\pm {\frac {1}{2}}\right\rangle }$	${\displaystyle \mp {\frac {2}{3}}\mu _{\rm {B}}B}$
${\displaystyle \left|{\frac {1}{2}},\pm {\frac {1}{2}}\right\rangle }$	${\displaystyle \left|{\frac {1}{2}},\mp {\frac {1}{2}}\right\rangle }$	${\displaystyle \pm {\frac {4}{3}}\mu _{\rm {B}}B}$
${\displaystyle \left|{\frac {3}{2}},\pm {\frac {3}{2}}\right\rangle }$	${\displaystyle \left|{\frac {1}{2}},\pm {\frac {1}{2}}\right\rangle }$	${\displaystyle \pm \mu _{\rm {B}}B}$
${\displaystyle \left|{\frac {3}{2}},\pm {\frac {1}{2}}\right\rangle }$	${\displaystyle \left|{\frac {1}{2}},\pm {\frac {1}{2}}\right\rangle }$	${\displaystyle \mp {\frac {1}{3}}\mu _{\rm {B}}B}$
${\displaystyle \left|{\frac {3}{2}},\pm {\frac {1}{2}}\right\rangle }$	${\displaystyle \left|{\frac {1}{2}},\mp {\frac {1}{2}}\right\rangle }$	${\displaystyle \pm {\frac {5}{3}}\mu _{\rm {B}}B}$

Эффект Пашена-Бака — это расщепление уровней атомной энергии в присутствии сильного магнитного поля. Это происходит, когда внешнее магнитное поле достаточно сильное, чтобы нарушить связь между орбитальным ( ) и спиновым ( ) моментами импульса. Этот эффект является пределом сильного поля эффекта Зеемана. Когда , два эффекта эквивалентны. Эффект был назван в честь немецких физиков Фридриха Пашена и Эрнста Э.А. Бака . ^[7]${\displaystyle {\vec {L}}}$${\displaystyle {\vec {S}}}$${\displaystyle s=0}$

Когда возмущение магнитного поля значительно превышает спин-орбитальное взаимодействие, можно смело предположить . Это позволяет легко оценить ожидаемые значения и для состояния . Энергии просто${\displaystyle [H_{0},S]=0}$${\displaystyle L_{z}}$${\displaystyle S_{z}}$${\displaystyle |\psi \rangle }$

${\displaystyle E_{z}=\left\langle \psi \left|H_{0}+{\frac {B_{z}\mu _{\rm {B}}}{\hbar }}(L_{z}+g_{s}S_{z})\right|\psi \right\rangle =E_{0}+B_{z}\mu _{\rm {B}}(m_{l}+g_{s}m_{s}).}$

Вышесказанное можно интерпретировать как подразумевающее, что LS-связь полностью разрушена внешним полем. Однако и все еще являются «хорошими» квантовыми числами. Вместе с правилами отбора для электрического дипольного перехода , т.е. это позволяет вообще игнорировать спиновую степень свободы. В результате будут видны только три спектральные линии, соответствующие правилу отбора. Расщепление не зависит от невозмущенных энергий и электронных конфигураций рассматриваемых уровней.${\displaystyle m_{l}}$${\displaystyle m_{s}}$${\displaystyle \Delta s=0,\Delta m_{s}=0,\Delta l=\pm 1,\Delta m_{l}=0,\pm 1}$${\displaystyle \Delta m_{l}=0,\pm 1}$${\displaystyle \Delta E=B\mu _{\rm {B}}\Delta m_{l}}$

Точнее, если , каждый из этих трех компонентов на самом деле является группой из нескольких переходов из-за остаточной спин-орбитальной связи и релятивистских поправок (которые имеют один и тот же порядок, известный как «тонкая структура»). Теория возмущений первого порядка с этими поправками дает следующую формулу для атома водорода в пределе Пашена-Бака: ^[8]${\displaystyle s\neq 0}$

${\displaystyle E_{z+fs}=E_{z}+{\frac {m_{e}c^{2}\alpha ^{4}}{2n^{3}}}\left\{{\frac {3}{4n}}-\left[{\frac {l(l+1)-m_{l}m_{s}}{l(l+1/2)(l+1)}}\right]\right\}.}$

В этом примере поправки на тонкую структуру игнорируются.

Дипольно-разрешенные переходы Лайман-альфа в режиме сильного поля

Начальное состояние ( )${\displaystyle n=2,l=1}$ ${\displaystyle \mid m_{l},m_{s}\rangle }$	Начальное энергетическое возмущение	Конечное состояние ( )${\displaystyle n=1,l=0}$ ${\displaystyle \mid m_{l},m_{s}\rangle }$	Конечное энергетическое возмущение
${\displaystyle \left|1,{\frac {1}{2}}\right\rangle }$	${\displaystyle +2\mu _{\rm {B}}B_{z}}$	${\displaystyle \left|0,{\frac {1}{2}}\right\rangle }$	${\displaystyle +\mu _{\rm {B}}B_{z}}$
${\displaystyle \left|0,{\frac {1}{2}}\right\rangle }$	${\displaystyle +\mu _{\rm {B}}B_{z}}$	${\displaystyle \left|0,{\frac {1}{2}}\right\rangle }$	${\displaystyle +\mu _{\rm {B}}B_{z}}$
${\displaystyle \left|1,-{\frac {1}{2}}\right\rangle }$	${\displaystyle 0}$	${\displaystyle \left|0,-{\frac {1}{2}}\right\rangle }$	${\displaystyle -\mu _{\rm {B}}B_{z}}$
${\displaystyle \left|-1,{\frac {1}{2}}\right\rangle }$	${\displaystyle 0}$	${\displaystyle \left|0,{\frac {1}{2}}\right\rangle }$	${\displaystyle +\mu _{\rm {B}}B_{z}}$
${\displaystyle \left|0,-{\frac {1}{2}}\right\rangle }$	${\displaystyle -\mu _{\rm {B}}B_{z}}$	${\displaystyle \left|0,-{\frac {1}{2}}\right\rangle }$	${\displaystyle -\mu _{\rm {B}}B_{z}}$
${\displaystyle \left|-1,-{\frac {1}{2}}\right\rangle }$	${\displaystyle -2\mu _{\rm {B}}B_{z}}$	${\displaystyle \left|0,-{\frac {1}{2}}\right\rangle }$	${\displaystyle -\mu _{\rm {B}}B_{z}}$

В приближении магнитного диполя гамильтониан, включающий как сверхтонкое , так и зеемановское взаимодействие, имеет вид

${\displaystyle H=hA{\vec {I}}\cdot {\vec {J}}-{\vec {\mu }}\cdot {\vec {B}}}$

${\displaystyle H=hA{\vec {I}}\cdot {\vec {J}}+(\mu _{\rm {B}}g_{J}{\vec {J}}+\mu _{\rm {N}}g_{I}{\vec {I}})\cdot {\vec {\rm {B}}}}$

где — сверхтонкое расщепление (в Гц) при нулевом приложенном магнитном поле, — магнетон Бора и ядерный магнетон соответственно, — операторы электронного и ядерного углового момента, — g-фактор Ланде :${\displaystyle A}$${\displaystyle \mu _{\rm {B}}}$${\displaystyle \mu _{\rm {N}}}$${\displaystyle {\vec {J}}}$${\displaystyle {\vec {I}}}$${\displaystyle g_{J}}$$${\displaystyle g_{J}=g_{L}{\frac {J(J+1)+L(L+1)-S(S+1)}{2J(J+1)}}+g_{S}{\frac {J(J+1)-L(L+1)+S(S+1)}{2J(J+1)}}.}$$

В случае слабых магнитных полей взаимодействие Зеемана можно рассматривать как возмущение базиса . В режиме сильного поля магнитное поле становится настолько сильным, что эффект Зеемана будет доминировать, и необходимо использовать более полный базис или просто так как и будет постоянным в пределах заданного уровня. ${\displaystyle |F,m_{f}\rangle }$${\displaystyle |I,J,m_{I},m_{J}\rangle }$${\displaystyle |m_{I},m_{J}\rangle }$${\displaystyle I}$${\displaystyle J}$

Чтобы получить полную картину, включая промежуточные значения напряженности поля, мы должны рассмотреть собственные состояния, которые являются суперпозициями базисных состояний и . Для гамильтониан можно решить аналитически, что приведет к формуле Брейта–Раби (названной в честь Грегори Брейта и Исидора Исаака Раби ). Примечательно, что электрическое квадрупольное взаимодействие равно нулю для ( ), поэтому эта формула довольно точна.${\displaystyle |F,m_{F}\rangle }$${\displaystyle |m_{I},m_{J}\rangle }$${\displaystyle J=1/2}$${\displaystyle L=0}$${\displaystyle J=1/2}$

Теперь мы используем квантово-механические лестничные операторы , которые определяются для общего оператора углового момента как${\displaystyle L}$

${\displaystyle L_{\pm }\equiv L_{x}\pm iL_{y}}$

Эти операторы лестниц имеют свойство

${\displaystyle L_{\pm }|L_{,}m_{L}\rangle ={\sqrt {(L\mp m_{L})(L\pm m_{L}+1)}}|L,m_{L}\pm 1\rangle }$

пока лежит в диапазоне (в противном случае они возвращают ноль). Используя операторы лестницы и Мы можем переписать гамильтониан как${\displaystyle m_{L}}$${\displaystyle {-L,\dots ...,L}}$${\displaystyle J_{\pm }}$${\displaystyle I_{\pm }}$

${\displaystyle H=hAI_{z}J_{z}+{\frac {hA}{2}}(J_{+}I_{-}+J_{-}I_{+})+\mu _{\rm {B}}Bg_{J}J_{z}+\mu _{\rm {N}}Bg_{I}I_{z}}$

Теперь мы можем видеть, что во все времена полная проекция углового момента будет сохраняться. Это происходит потому, что и оставляют состояния с определенным и неизменными, в то время как и либо увеличиваются , либо уменьшаются, либо наоборот, поэтому сумма всегда остается неизменной. Кроме того, поскольку существует только два возможных значения , которые являются . Следовательно, для каждого значения существует только два возможных состояния, и мы можем определить их как основу:${\displaystyle m_{F}=m_{J}+m_{I}}$${\displaystyle J_{z}}$${\displaystyle I_{z}}$${\displaystyle m_{J}}$${\displaystyle m_{I}}$${\displaystyle J_{+}I_{-}}$${\displaystyle J_{-}I_{+}}$${\displaystyle m_{J}}$${\displaystyle m_{I}}$${\displaystyle J=1/2}$${\displaystyle m_{J}}$${\displaystyle \pm 1/2}$${\displaystyle m_{F}}$

${\displaystyle |\pm \rangle \equiv |m_{J}=\pm 1/2,m_{I}=m_{F}\mp 1/2\rangle }$

Эта пара состояний представляет собой двухуровневую квантово-механическую систему . Теперь мы можем определить матричные элементы гамильтониана:

${\displaystyle \langle \pm |H|\pm \rangle =-{\frac {1}{4}}hA+\mu _{\rm {N}}Bg_{I}m_{F}\pm {\frac {1}{2}}(hAm_{F}+\mu _{\rm {B}}Bg_{J}-\mu _{\rm {N}}Bg_{I}))}$

${\displaystyle \langle \pm |H|\mp \rangle ={\frac {1}{2}}hA{\sqrt {(I+1/2)^{2}-m_{F}^{2}}}}$

Решая собственные значения этой матрицы — что можно сделать вручную (см. двухуровневую квантово-механическую систему ) или, что проще, с помощью системы компьютерной алгебры — мы приходим к энергетическим сдвигам:

${\displaystyle \Delta E_{F=I\pm 1/2}=-{\frac {h\Delta W}{2(2I+1)}}+\mu _{\rm {N}}g_{I}m_{F}B\pm {\frac {h\Delta W}{2}}{\sqrt {1+{\frac {2m_{F}x}{I+1/2}}+x^{2}}}}$

${\displaystyle x\equiv {\frac {B(\mu _{\rm {B}}g_{J}-\mu _{\rm {N}}g_{I})}{h\Delta W}}\quad \quad \Delta W=A\left(I+{\frac {1}{2}}\right)}$

где — расщепление (в единицах Гц) между двумя сверхтонкими подуровнями в отсутствие магнитного поля , называется «параметром напряженности поля» (Примечание: для выражения под квадратным корнем — это точный квадрат, и поэтому последний член следует заменить на ). Это уравнение известно как формула Брейта–Раби и полезно для систем с одним валентным электроном на уровне ( ). ^{[9] [10]}${\displaystyle \Delta W}$${\displaystyle B}$${\displaystyle x}$${\displaystyle m_{F}=\pm (I+1/2)}$${\displaystyle +{\frac {h\Delta W}{2}}(1\pm x)}$${\displaystyle s}$${\displaystyle J=1/2}$

Обратите внимание, что индекс в следует рассматривать не как полный угловой момент атома, а как асимптотический полный угловой момент . Он равен полному угловому моменту только в том случае, если в противном случае собственные векторы, соответствующие различным собственным значениям гамильтониана, являются суперпозициями состояний с различными, но равными (исключение составляют только ).${\displaystyle F}$${\displaystyle \Delta E_{F=I\pm 1/2}}$${\displaystyle B=0}$${\displaystyle F}$${\displaystyle m_{F}}$${\displaystyle |F=I+1/2,m_{F}=\pm F\rangle }$

Джордж Эллери Хейл был первым, кто заметил эффект Зеемана в солнечных спектрах, что указывает на существование сильных магнитных полей в солнечных пятнах. Такие поля могут быть довольно высокими, порядка 0,1 тесла и выше. Сегодня эффект Зеемана используется для получения магнитограмм, показывающих изменение магнитного поля на Солнце, ^{[ необходима цитата ]} и для анализа геометрии магнитного поля в других звездах. ^[11]

Эффект Зеемана используется во многих приложениях лазерного охлаждения , таких как магнитооптическая ловушка и замедлитель Зеемана . ^{[ необходима ссылка ]}

Связь спиновых и орбитальных движений, опосредованная энергией Зеемана, используется в спинтронике для управления электронными спинами в квантовых точках посредством электрического дипольного спинового резонанса . ^[12]

Старые высокоточные стандарты частоты, то есть атомные часы на основе сверхтонкой структуры перехода, могут потребовать периодической тонкой настройки из-за воздействия магнитных полей. Это осуществляется путем измерения эффекта Зеемана на определенных уровнях сверхтонкой структуры перехода исходного элемента (цезия) и применения равномерно точного, слабого магнитного поля к указанному источнику в процессе, известном как размагничивание . ^[13]

Эффект Зеемана также может быть использован для повышения точности в атомно-абсорбционной спектроскопии . ^{[ необходима ссылка ]}

Теория о магнитном чувстве птиц предполагает, что белок в сетчатке глаза изменяется из-за эффекта Зеемана. ^[14]

Ядерный эффект Зеемана важен в таких приложениях, как спектроскопия ядерного магнитного резонанса , магнитно-резонансная томография (МРТ) и мёссбауэровская спектроскопия . ^{[ необходима ссылка ]}

Спектроскопия электронного спинового резонанса основана на эффекте Зеемана. ^{[ необходима ссылка ]}

Эффект Зеемана можно продемонстрировать, поместив источник паров натрия в мощный электромагнит и наблюдая за лампой с парами натрия через отверстие магнита (см. схему). При выключенном магните источник паров натрия будет блокировать свет лампы; при включенном магните свет лампы будет виден через пар.

Пары натрия можно получить, запечатав металлический натрий в откачанной стеклянной трубке и нагревая его, пока трубка находится в магните. ^[15]

В качестве альтернативы, соль ( хлорид натрия ) на керамической палочке можно поместить в пламя горелки Бунзена в качестве источника паров натрия. Когда магнитное поле активируется, изображение лампы будет ярче. ^[16] Однако магнитное поле также влияет на пламя, делая наблюдение зависящим не только от эффекта Зеемана. ^[15] Эти проблемы также мешали оригинальной работе Зеемана; он приложил значительные усилия, чтобы убедиться, что его наблюдения действительно являются эффектом магнетизма на излучение света. ^[17]

Когда соль добавляется в горелку Бунзена, она диссоциирует , давая натрий и хлорид . Атомы натрия возбуждаются из-за фотонов из натриевой лампы, при этом электроны возбуждаются из состояний 3s в 3p, поглощая свет в процессе. Натриевая лампа излучает свет с длиной волны 589 нм, который имеет как раз ту энергию, чтобы возбудить электрон атома натрия. Если бы это был атом другого элемента, например хлора, тень не образовалась бы. ^{[18] [ неудачная проверка ]} При приложении магнитного поля из-за эффекта Зеемана спектральная линия натрия расщепляется на несколько компонентов. Это означает, что разница в энергии между атомными орбиталями 3s и 3p изменится. Поскольку натриевая лампа больше не обеспечивает точную частоту, свет не поглощается и проходит, что приводит к затемнению тени. По мере увеличения напряженности магнитного поля сдвиг спектральных линий увеличивается, и свет лампы передается. ^{[ необходима цитата ]}

На Викискладе есть медиафайлы по теме «Эффект Зеемана» .

• Магнитооптический эффект Керра
• эффект Фойгта
• эффект Фарадея
• Эффект хлопка-мутона
• Поляризационная спектроскопия
• энергия Зеемана
• Эффект Старка
• Ягненок сдвиг

• Кондон, Э.У.; Г. Х. Шортли (1935). Теория атомных спектров . Издательство Кембриджского университета . ISBN 0-521-09209-4. (Глава 16 содержит всестороннее рассмотрение по состоянию на 1935 год.)
• Зееман, П. (1896). «О влиянии магнетизма на природу света, излучаемого веществом». Verslagen van de Gewone Vergaderingen der Wis- en Natuurkundige Afdeeling (Koninklijk Akademie van Wetenschappen te Amsterdam) [Отчеты очередных сессий математической и физической секции (Королевской академии наук в Амстердаме)] (на голландском языке). 5 : 181–184 и 242–248. Бибкод : 1896ВМКАН...5..181Z.
• Зееман, П. (1897). «О влиянии магнетизма на природу света, испускаемого веществом». Philosophical Magazine . 5-я серия. 43 (262): 226– 239. doi :10.1080/14786449708620985.
• Зееман, П. (11 февраля 1897 г.). "Влияние намагничивания на природу света, испускаемого веществом". Nature . 55 (1424): 347. Bibcode :1897Natur..55..347Z. doi : 10.1038/055347a0 .
• Зееман, П. (1897). «О дублетах и ​​тройках в тепловом спектре, teweeggebracht Door uitwendige Magneticische krachten» [О дублетах и ​​тройках в спектре, вызванных внешними магнитными силами]. Verslagen van de Gewone Vergaderingen der Wis- en Natuurkundige Afdeeling (Koninklijk Akademie van Wetenschappen te Amsterdam) [Отчеты очередных сессий математической и физической секции (Королевской академии наук в Амстердаме)] (на голландском языке). 6 : 13–18 , 99–102 и 260–262.
• Зееман, П. (1897). «Дуплет и триплет в спектре, создаваемом внешними магнитными силами». Philosophical Magazine . 5-я серия. 44 (266): 55– 60. doi :10.1080/14786449708621028.

• Фейнман, Ричард ; Лейтон, Роберт Б.; Сэндс , Мэтью (1989). Лекции Фейнмана по физике. Том 3. Эддисон-Уэсли . ISBN 0-201-02115-3.
• Форман, Пол (1970). «Альфред Ланде и аномальный эффект Зеемана, 1919-1921». Исторические исследования в области физических наук . 2 : 153– 261. doi :10.2307/27757307. JSTOR  27757307.
• Гриффитс, Дэвид Дж. (2004). Введение в квантовую механику (2-е изд.). Prentice Hall . ISBN 0-13-805326-X.
• Либофф, Ричард Л. (2002). Введение в квантовую механику (4-е изд.). Эддисон-Уэсли . ISBN 0-8053-8714-5. OCLC  50475492.
• Собельман, Игорь И. (2006). Теория атомных спектров . Alpha Science. ISBN 1-84265-203-6. OCLC  71825022.
• Фут, К. Дж. (2005). Атомная физика. OUP Oxford. ISBN 0-19-850696-1. OCLC  57478010.

• Эффект Зеемана - Управление светом с помощью магнитных полей