Спинтроника
Спинтроника ( гибридное слово, означающее спиновая транспортная электроника [1] [2] [3] ), также известная как спиновая электроника , является изучением собственного спина электрона и связанного с ним магнитного момента , в дополнение к его фундаментальному электронному заряду , в твердотельных устройствах . [4] Область спинтроники касается спин-зарядовой связи в металлических системах; аналогичные эффекты в изоляторах попадают в область мультиферроиков .
Спинтроника принципиально отличается от традиционной электроники тем, что в дополнение к зарядовому состоянию электронные спины используются как дополнительная степень свободы, что влияет на эффективность хранения и передачи данных. Спинтронные системы чаще всего реализуются в разбавленных магнитных полупроводниках (DMS) и сплавах Гейслера и представляют особый интерес в области квантовых вычислений и нейроморфных вычислений .
История
Спинтроника возникла из открытий 1980-х годов, касающихся спин-зависимых явлений электронного транспорта в твердотельных устройствах. Сюда входит наблюдение спин-поляризованной инжекции электронов из ферромагнитного металла в нормальный металл Джонсоном и Силсби (1985) [5] и открытие гигантского магнитосопротивления независимо Альбертом Фертом и др. [6] и Питером Грюнбергом и др. (1988). [7] Происхождение спинтроники можно проследить до экспериментов по туннелированию ферромагнетиков/сверхпроводников, впервые проведенных Месерви и Тедроу, и первых экспериментов по магнитным туннельным переходам Жюльером в 1970-х годах. [8] Использование полупроводников для спинтроники началось с теоретического предложения транзистора со спиновым полем Даттой и Дасом в 1990 году [9] и электрического дипольного спинового резонанса Рашбой в 1960 году. [10]
Теория
Спин электрона — это собственный угловой момент , который отделен от углового момента из-за его орбитального движения. Величина проекции спина электрона вдоль произвольной оси равна , что подразумевает, что электрон действует как фермион по теореме о спиновой статистике . Подобно орбитальному угловому моменту, спин имеет связанный магнитный момент , величина которого выражается как
- .
В твердом теле спины многих электронов могут действовать совместно, влияя на магнитные и электронные свойства материала, например, наделяя его постоянным магнитным моментом, как в ферромагнетике .
Во многих материалах электронные спины присутствуют в равной степени как в состоянии вверх, так и в состоянии вниз, и никакие транспортные свойства не зависят от спина. Спинтронное устройство требует генерации или манипуляции спин-поляризованной популяцией электронов, что приводит к избытку спин-вверх или спин-вниз электронов. Поляризация любого спин-зависимого свойства X может быть записана как
- .
Чистая спиновая поляризация может быть достигнута либо путем создания равновесного энергетического разделения между спином вверх и спином вниз. Методы включают помещение материала в большое магнитное поле ( эффект Зеемана ), обменную энергию, присутствующую в ферромагнетике, или вытеснение системы из равновесия. Период времени, в течение которого может поддерживаться такая неравновесная популяция, известен как время жизни спина, .
В диффузионном проводнике длина диффузии спина может быть определена как расстояние, на которое может распространяться неравновесная спиновая популяция. Спиновые времена жизни электронов проводимости в металлах относительно короткие (обычно менее 1 наносекунды). Важное направление исследований посвящено продлению этого времени жизни до технологически значимых временных масштабов.
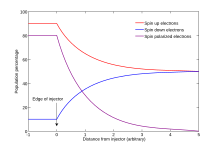
Механизмы распада для спин-поляризованной популяции можно в целом классифицировать как рассеяние с переворотом спина и спиновую дефазировку. Рассеяние с переворотом спина — это процесс внутри твердого тела, который не сохраняет спин и, следовательно, может переключать входящее состояние со спином вверх в исходящее состояние со спином вниз. Спиновая дефазировка — это процесс, при котором популяция электронов с общим спиновым состоянием становится менее поляризованной с течением времени из-за различных скоростей прецессии электронного спина . В ограниченных структурах спиновая дефазировка может быть подавлена, что приводит к временам жизни спина в миллисекундах в полупроводниковых квантовых точках при низких температурах.
Сверхпроводники могут усиливать центральные эффекты в спинтронике, такие как эффекты магнитосопротивления, время жизни спина и бездиссипативные спиновые токи. [11] [12]
Самый простой способ создания спин-поляризованного тока в металле — пропускание тока через ферромагнитный материал. Наиболее распространенные приложения этого эффекта включают устройства с гигантским магнитосопротивлением (GMR). Типичное устройство GMR состоит как минимум из двух слоев ферромагнитных материалов, разделенных разделительным слоем. Когда два вектора намагниченности ферромагнитных слоев выровнены, электрическое сопротивление будет ниже (поэтому при постоянном напряжении течет более высокий ток), чем если бы ферромагнитные слои были антивыровнены. Это представляет собой датчик магнитного поля.
В устройствах применяются два варианта GMR: (1) ток в плоскости (CIP), где электрический ток течет параллельно слоям, и (2) ток перпендикулярно плоскости (CPP), где электрический ток течет в направлении, перпендикулярном слоям.
Другие устройства спинтроники на основе металлов:
- Туннельное магнитосопротивление (TMR), при котором транспорт CPP достигается с помощью квантово-механического туннелирования электронов через тонкий изолятор, разделяющий ферромагнитные слои.
- Спин-перенос крутящего момента , при котором ток спин-поляризованных электронов используется для управления направлением намагничивания ферромагнитных электродов в устройстве.
- Спин-волновые логические устройства переносят информацию в фазе. Интерференция и спин-волновое рассеяние могут выполнять логические операции.
Спинтронно-логические устройства
Энергонезависимые спин-логические устройства, обеспечивающие масштабирование, активно изучаются. [13] Были предложены спин-переносные, основанные на крутящем моменте логические устройства, которые используют спины и магниты для обработки информации. [14] [15] Эти устройства являются частью исследовательской дорожной карты ITRS . Приложения логической памяти уже находятся на стадии разработки. [16] [17] Обзорную статью 2017 года можно найти в Materials Today . [4]
Была предложена обобщенная теория цепей для спинтронных интегральных схем [18], так что физика спинового транспорта может быть использована разработчиками SPICE, а затем и проектировщиками схем и систем для исследования спинтроники «за пределами КМОП-вычислений».
Приложения
Считывающие головки магнитных жестких дисков работают на основе эффекта GMR или TMR.
Motorola разработала первое поколение магниторезистивной памяти с произвольным доступом (MRAM) объемом 256 кб на основе одного магнитного туннельного перехода и одного транзистора, который имеет цикл чтения/записи менее 50 наносекунд. [19] С тех пор Everspin разработала версию объемом 4 Мб . [20] В настоящее время разрабатываются две технологии MRAM второго поколения: переключение с помощью термопары (TAS) [21] и передача крутящего момента спина (STT). [22]
Другая конструкция, «гоночная память» , новая архитектура памяти, предложенная доктором Стюартом С. П. Паркиным , кодирует информацию в направлении намагничивания между доменными стенками ферромагнитного провода.
В 2012 году удалось добиться того, что постоянные спиновые спирали синхронизированных электронов сохранялись более наносекунды, что в 30 раз больше, чем в предыдущих попытках, и дольше, чем продолжительность тактового цикла современного процессора. [23]
Спинтронные устройства на основе полупроводников
Легированные полупроводниковые материалы демонстрируют разбавленный ферромагнетизм. В последние годы разбавленные магнитные оксиды (DMO), включая DMO на основе ZnO и DMO на основе TiO 2 , стали предметом многочисленных экспериментальных и вычислительных исследований. [24] [25] Неоксидные ферромагнитные полупроводниковые источники (например, легированный марганцем арсенид галлия (Ga,Mn)As ), [26] увеличивают сопротивление интерфейса с помощью туннельного барьера, [27] или с помощью инжекции горячих электронов. [28]
Обнаружение спина в полупроводниках решалось с помощью нескольких методов:
- Вращение Фарадея/Керра прошедших/отражённых фотонов [29]
- Анализ круговой поляризации электролюминесценции [30]
- Нелокальный спиновый клапан (адаптировано из работы Джонсона и Силсби с металлами) [31]
- Баллистическая спиновая фильтрация [32]
Последняя технология была использована для преодоления недостатка спин-орбитального взаимодействия и проблем с материалами для достижения спинового транспорта в кремнии . [33]
Поскольку внешние магнитные поля (и поля рассеяния от магнитных контактов) могут вызывать большие эффекты Холла и магнитосопротивление в полупроводниках (которые имитируют эффекты спинового клапана ), единственным убедительным доказательством спинового переноса в полупроводниках является демонстрация прецессии спина и дефазировки в магнитном поле, неколлинеарном ориентации инжектированного спина, что называется эффектом Ханле .
Приложения
Приложения, использующие спин-поляризованную электрическую инжекцию, показали снижение порогового тока и управляемый циркулярно поляризованный когерентный световой выход. [34] Примерами могут служить полупроводниковые лазеры. Будущие приложения могут включать транзистор на основе спина, имеющий преимущества по сравнению с устройствами MOSFET, такими как более крутой подпороговый наклон.
Магнитно-туннельный транзистор : Магнитно-туннельный транзистор с одним базовым слоем [35] имеет следующие выводы:
- Эмиттер (FM1): инжектирует спин-поляризованные горячие электроны в базу.
- База (FM2): В базе происходит спин-зависимое рассеяние. Она также служит спиновым фильтром.
- Коллектор (GaAs): На интерфейсе формируется барьер Шоттки . Он собирает только те электроны, которые имеют достаточно энергии для преодоления барьера Шоттки, и когда в полупроводнике имеются состояния.
Магнитоток (MC) определяется как:
А передаточное отношение (TR) равно
МТТ обещает источник электронов с высокой спиновой поляризацией при комнатной температуре.
Носители информации
Антиферромагнитные носители информации изучались как альтернатива ферромагнетизму , [36] особенно потому, что с антиферромагнитным материалом биты могут храниться так же, как и с ферромагнитным материалом. Вместо обычного определения 0 ↔ 'намагничивание вверх', 1 ↔ 'намагничивание вниз', состояния могут быть, например, 0 ↔ 'вертикально-чередующаяся спиновая конфигурация' и 1 ↔ 'горизонтально-чередующаяся спиновая конфигурация'. [37] ).
Основными преимуществами антиферромагнитного материала являются:
- нечувствительность к возмущениям, повреждающим данные, вызванным полями рассеяния из-за нулевой чистой внешней намагниченности; [38]
- отсутствие влияния на близлежащие частицы, что означает, что элементы антиферромагнитного устройства не будут оказывать магнитного воздействия на соседние элементы; [38]
- гораздо более короткое время переключения (частота антиферромагнитного резонанса находится в диапазоне ТГц по сравнению с частотой ферромагнитного резонанса ГГц); [39]
- широкий спектр общедоступных антиферромагнитных материалов, включая изоляторы, полупроводники, полуметаллы, металлы и сверхпроводники. [39]
Проводятся исследования того, как считывать и записывать информацию в антиферромагнитную спинтронику, поскольку их чистая нулевая намагниченность делает это сложным по сравнению с обычной ферромагнитной спинтроникой. В современной MRAM обнаружение и манипулирование ферромагнитным порядком с помощью магнитных полей в значительной степени было оставлено в пользу более эффективного и масштабируемого считывания и записи с помощью электрического тока. Методы считывания и записи информации с помощью тока, а не полей также исследуются в антиферромагнетиках, поскольку поля в любом случае неэффективны. Методы записи, которые в настоящее время исследуются в антиферромагнетиках, основаны на крутящем моменте спиновой передачи и крутящем моменте спиновой орбиты из спинового эффекта Холла и эффекта Рашбы . Также изучается считывание информации в антиферромагнетиках с помощью эффектов магнитосопротивления, таких как туннельное магнитосопротивление . [40]
Смотрите также
- Стюарт СП Паркин
- Электрический дипольный спиновый резонанс
- эффект Джозефсона
- Магниторезистивная память с произвольным доступом (MRAM)
- Магноника
- Потенциальные применения графена#Спинтроника
- Эффект Рашбы
- Спиновая накачка
- Крутящий момент при передаче вращения
- Спинхендж@Дома
- Спинмехатроника
- Спинплазмоника
- Нетрадиционные вычисления
- Валлейтроника
- Список новых технологий
- Мультиферроики
Ссылки
- ^ Вольф, СА; Щелканова, АЮ; Трегер, ДМ (2006). «Спинтроника — ретроспектива и перспектива». IBM Journal of Research and Development . 50 : 101–110. doi :10.1147/rd.501.0101.
- ^ "Physics Profile: "Stu Wolf: True D! Hollywood Story"". Архивировано из оригинала 18 апреля 2011 года . Получено 11 июля 2008 года .
- ^ Spintronics: A Spin-Based Electronics Vision for the Future. Sciencemag.org (16 ноября 2001 г.). Получено 21 октября 2013 г.
- ^ ab Bhatti, S.; et al. (2017). «Оперативная память на основе спинтроники: обзор». Materials Today . 20 (9): 530–548. doi : 10.1016/j.mattod.2017.07.007 . hdl : 10356/146755 .
- ^ Джонсон, М.; Силсби, Р. Х. (1985). «Интерфейсная зарядово-спиновая связь: инжекция и обнаружение спиновой намагниченности в металлах». Physical Review Letters . 55 (17): 1790–1793. Bibcode :1985PhRvL..55.1790J. doi :10.1103/PhysRevLett.55.1790. PMID 10031924.
- ^ Байбич, М. Н.; Брото, Дж. М.; Ферт, А.; Нгуен Ван Дау, Ф.; Петрофф, Ф.; Этьен, П.; Крезе, Г.; Фридерих, А.; Шазелас, Дж. (1988). "Гигантское магнитосопротивление магнитных сверхрешеток (001)Fe/(001)Cr" (PDF) . Physical Review Letters . 61 (21): 2472–2475. Bibcode :1988PhRvL..61.2472B. doi : 10.1103/PhysRevLett.61.2472 . PMID 10039127.
- ^ Бинаш, Г.; Грюнберг, П.; Зауренбах, Ф.; Цинн, В. (1989). «Повышенное магнитосопротивление в слоистых магнитных структурах с антиферромагнитным межслойным обменом». Physical Review B. 39 ( 7): 4828–4830. Bibcode : 1989PhRvB..39.4828B. doi : 10.1103/PhysRevB.39.4828 . PMID 9948867.
- ^ Julliere, M. (1975). «Туннелирование между ферромагнитными пленками». Physics Letters A. 54 ( 3): 225–226. Bibcode : 1975PhLA...54..225J. doi : 10.1016/0375-9601(75)90174-7.
- ^ Датта, С. и Дас, Б. (1990). «Электронный аналог электрооптического модулятора». Applied Physics Letters . 56 (7): 665–667. Bibcode : 1990ApPhL..56..665D. doi : 10.1063/1.102730.
- ^ EI Rashba, Циклотронный и комбинированный резонансы в перпендикулярном поле, Sov. Phys. Solid State 2 , 1109 -1122 (1960)
- ^ Линдер, Якоб; Робинсон, Джейсон WA (2 апреля 2015 г.). «Сверхпроводящая спинтроника». Nature Physics . 11 (4): 307–315. arXiv : 1510.00713 . Bibcode : 2015NatPh..11..307L. doi : 10.1038/nphys3242. ISSN 1745-2473. S2CID 31028550.
- ^ Эшриг, Маттиас (2011). «Спин-поляризованные сверхтоки для спинтроники». Physics Today . 64 (1): 43–49. Bibcode : 2011PhT....64a..43E. doi : 10.1063/1.3541944.
- ^ Международная технологическая дорожная карта для полупроводников
- ^ Бехин-Аейн, Б.; Датта, Д.; Салахуддин, С.; Датта, С. (2010). «Предложение о логическом устройстве со всеми спинами и встроенной памятью». Nature Nanotechnology . 5 (4): 266–270. Bibcode : 2010NatNa...5..266B. doi : 10.1038/nnano.2010.31. PMID 20190748.
- ^ Манипатруни, Сасикант; Никонов, Дмитрий Э. и Янг, Ян А. (2011) [1112.2746] Теория цепей для SPICE интегральных схем спинтроники. Arxiv.org. Получено 21 октября 2013 г.
- ^ Crocus сотрудничает со Starchip для разработки системных решений на основе технологии магнитных логических устройств (MLU). crocus-technology.com. 8 декабря 2011 г.
- ^ Инновационная новая технология для повышения надежности логических интегральных схем спинтроники. Nec.com. 11 июня 2012 г.
- ^ S. Manipatruni, DE Nikonov и IA Young, «Моделирование и проектирование интегральных схем спинтроники», в IEEE Transactions on Circuits and Systems I: Regular Papers, т. 59, № 12, стр. 2801-2814, декабрь 2012 г., doi: 10.1109/TCSI.2012.2206465. https://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=6359950&isnumber=6359940
- ^ Spintronics. Sigma-Aldrich. Получено 21 октября 2013 г.
- ↑ Everspin Архивировано 30 июня 2012 года на Wayback Machine . Everspin. Получено 21 октября 2013 года.
- ^ Хоберман, Барри. Возникновение практической MRAM Архивировано 21 октября 2013 г. в Wayback Machine . crocustechnology.com
- ^ ЛаПедус, Марк (18 июня 2009 г.) Tower инвестирует в Crocus, советует сделку по литейному производству MRAM. eetimes.com
- ^ Walser, M.; Reichl, C.; Wegscheider, W. & Salis, G. (2012). "Прямое отображение образования устойчивой спиновой спирали". Nature Physics . 8 (10): 757. arXiv : 1209.4857 . Bibcode :2012NatPh...8..757W. doi :10.1038/nphys2383. S2CID 119209785.
- ^ Assadi, MHN; Hanaor, DAH (2013). «Теоретическое исследование энергетики и магнетизма меди в полиморфах TiO 2 ». Журнал прикладной физики . 113 (23): 233913–233913–5. arXiv : 1304.1854 . Bibcode : 2013JAP...113w3913A. doi : 10.1063/1.4811539. S2CID 94599250.
- ^ Огале, СБ (2010). «Разбавленное легирование, дефекты и ферромагнетизм в системах оксидов металлов». Advanced Materials . 22 (29): 3125–3155. Bibcode : 2010AdM....22.3125O. doi : 10.1002/adma.200903891. PMID 20535732. S2CID 25307693.
- ^ Jonker, B.; Park, Y.; Bennett, B.; Cheong, H.; Kioseoglou, G.; Petrou, A. (2000). «Надежная электрическая спиновая инжекция в полупроводниковую гетероструктуру». Physical Review B. 62 ( 12): 8180. Bibcode : 2000PhRvB..62.8180J. doi : 10.1103/PhysRevB.62.8180.
- ^ Hanbicki, AT; Jonker, BT; Itskos, G.; Kioseoglou, G.; Petrou, A. (2002). "Эффективная электрическая спиновая инжекция из контакта магнитного металла/туннельного барьера в полупроводник". Applied Physics Letters . 80 (7): 1240. arXiv : cond-mat/0110059 . Bibcode : 2002ApPhL..80.1240H. doi : 10.1063/1.1449530. S2CID 119098659.
- ^ Jiang, X.; Wang, R.; Van Dijken, S.; Shelby, R.; MacFarlane, R.; Solomon, G.; Harris, J.; Parkin, S. (2003). "Оптическое обнаружение инжекции спина горячих электронов в GaAs из источника на основе магнитного туннельного транзистора". Physical Review Letters . 90 (25): 256603. Bibcode : 2003PhRvL..90y6603J. doi : 10.1103/PhysRevLett.90.256603. PMID 12857153.
- ^ Kikkawa, J.; Awschalom, D. (1998). "Резонансное спиновое усиление в n-типе GaAs". Physical Review Letters . 80 (19): 4313. Bibcode : 1998PhRvL..80.4313K. doi : 10.1103/PhysRevLett.80.4313.
- ^ Йонкер, Беренд Т. Поляризованное оптическое излучение, вызванное распадом или рекомбинацией спин-поляризованных инжектированных носителей – Патент США 5874749 Архивировано 12 декабря 2009 г. в Wayback Machine . Выдано 23 февраля 1999 г.
- ^ Lou, X.; Adelmann, C.; Crooker, SA; Garlid, ES; Zhang, J.; Reddy, KSM; Flexner, SD; Palmstrøm, CJ; Crowell, PA (2007). "Электрическое обнаружение спинового транспорта в латеральных ферромагнетиках–полупроводниковых устройствах". Nature Physics . 3 (3): 197. arXiv : cond-mat/0701021 . Bibcode :2007NatPh...3..197L. doi :10.1038/nphys543. S2CID 51390849.
- ^ Аппельбаум, И.; Хуан, Б.; Монсма, DJ (2007). «Электронное измерение и управление спиновым транспортом в кремнии». Nature . 447 (7142): 295–298. arXiv : cond-mat/0703025 . Bibcode :2007Natur.447..295A. doi :10.1038/nature05803. PMID 17507978. S2CID 4340632.
- ^ Жутич, И.; Фабиан, Дж. (2007). «Спинтроника: кремниевые повороты». Природа . 447 (7142): 268–269. Бибкод : 2007Natur.447..268Z. дои : 10.1038/447269а . PMID 17507969. S2CID 32830840.
- ^ Holub, M.; Shin, J.; Saha, D.; Bhattacharya, P. (2007). «Электрическая спиновая инжекция и снижение порога в полупроводниковом лазере». Physical Review Letters . 98 (14): 146603. Bibcode : 2007PhRvL..98n6603H. doi : 10.1103/PhysRevLett.98.146603. PMID 17501298.
- ^ Ван Дейкен, С.; Цзян, Х.; Паркин, ССП (2002). «Работа магнитного туннельного транзистора с высоким выходным током при комнатной температуре». Applied Physics Letters . 80 (18): 3364. Bibcode : 2002ApPhL..80.3364V. doi : 10.1063/1.1474610.
- ^ Jungwirth, T. (28 апреля 2014 г.). "Relativistic Approaches to Spintronics with Antiferromagnets" (PDF) (объявление о коллоквиуме по физике в Баварском университете). Архивировано из оригинала (PDF) 29 апреля 2014 г. . Получено 29 апреля 2014 г. .
- ^ Математически это соответствует переходу от группы вращения SO(3) к ее релятивистскому покрытию, «двойной группе» SU(2)
- ^ ab Jungwirth, T.; Marti, X.; Wadley, P.; Wunderlich, J. (2016). «Антиферромагнитная спинтроника». Nature Nanotechnology . 11 (3). Springer Nature: 231–241. arXiv : 1509.05296 . Bibcode :2016NatNa..11..231J. doi :10.1038/nnano.2016.18. ISSN 1748-3387. PMID 26936817. S2CID 5058124.
- ^ ab Gomonay, O.; Jungwirth, T.; Sinova, J. (21 февраля 2017 г.). "Концепции антиферромагнитной спинтроники". Physica Status Solidi RRL . 11 (4). Wiley: 1700022. arXiv : 1701.06556 . Bibcode : 2017PSSRR..1100022G. doi : 10.1002/pssr.201700022. ISSN 1862-6254. S2CID 73575617.
- ^ Chappert, Claude; Fert, Albert; van Dau, Frédéric Nguyen (2007). «Возникновение спиновой электроники в хранении данных». Nature Materials . 6 (11). Springer Science and Business Media LLC: 813–823. Bibcode :2007NatMa...6..813C. doi :10.1038/nmat2024. ISSN 1476-1122. PMID 17972936. S2CID 21075877.
Дальнейшее чтение
- «Введение в спинтронику». Марк Кахай, Суприйо Бандиопадхьяй, CRC Press, ISBN 0-8493-3133-1
- JA Gupta; R. Knobel; N. Samarth; DD Awschalom (29 июня 2001 г.). «Сверхбыстрое манипулирование когерентностью электронного спина». Science . 292 (5526): 2458–2461. Bibcode :2001Sci...292.2458G. doi :10.1126/science.1061169. PMID 11431559. S2CID 22898874.
- Wolf, SA; Awschalom, DD; Buhrman, RA; Daughton, JM; von Molnár, S; Roukes, ML; Chtchelkanova, AY; Treger, DM (16 ноября 2001 г.). "Spintronics: A Spin-Based Electronics Vision for the Future". Science . 294 (5546): 1488–1495. Bibcode :2001Sci...294.1488W. doi :10.1126/science.1065389. PMID 11711666. S2CID 14010432.
- Шарма, П. (28 января 2005 г.). «Как создать спиновый ток». Science . 307 (5709): 531–533. doi :10.1126/science.1099388. PMID 15681374. S2CID 118636399.
- Томаш Дитль; Дэвид Д. Авшалом; Мария Каминская; и др., ред. (2009). Спинтроника. Академическая пресса . ISBN 9780080914213.
- Žutić, I.; Das Sarma, S. (2004). «Спинтроника: основы и приложения». Reviews of Modern Physics . 76 (2): 323–410. arXiv : cond-mat/0405528 . Bibcode :2004RvMP...76..323Z. doi :10.1103/RevModPhys.76.323. S2CID 119398474.
- Паркин, Стюарт; Чинг-Рей, Чанг; Чантрелл, Рой, ред. (2011). "SPIN". World Scientific. ISSN 2010-3247.
{{cite journal}}: Цитировать журнал требует|journal=( помощь ) - «Спинтроника делает шаг вперед», Новости Университета Южной Флориды
- Бадер, SD; Паркин, SSP (2010). «Спинтроника». Ежегодный обзор физики конденсированных сред . 1 : 71–88. Bibcode : 2010ARCMP...1...71B. doi : 10.1146/annurev-conmatphys-070909-104123.
Внешние ссылки
- 23 вехи в истории спина, составленные Nature
- Веха 18: Гигантский скачок для электроники: гигантское магнитосопротивление, составлено Nature
- Веха 20: Информация в спине: Датта-Дас, составлено Nature
- Авшалом, Дэвид Д.; Флатте, Майкл Э.; Самарт, Нитин (июнь 2002 г.). «Спинтроника». Научный американец . 286 (6): 66–73. Бибкод : 2002SciAm.286f..66A. doi : 10.1038/scientificamerican0602-66. ПМИД 12030093.
- Портал Spintronics с новостями и ресурсами
- RaceTrack:InformationWeek (11 апреля 2008 г.) Архивировано 14 апреля 2008 г. в Wayback Machine
- Исследования спинтроники нацелены на GaAs.
- Учебное пособие по спинтронике
- Лекция о спиновом транспорте, автор С. Датта (из транзистора Датта Дас) — Часть 1 и Часть 2






