Дуопризма

Набор однородных pq дуопризм
Тип	Призматические однородные 4-мерные многогранники
Символ Шлефли	{ п }×{ д }
Диаграмма Коксетера-Дынкина
Клетки	pq -угольные призмы , qp -угольные призмы
Лица	pq квадраты , pq -угольники, qp -угольники
Края	2 пк
Вершины	пк
Вершинная фигура	дисфеноидный
Симметрия	[ p ,2, q ] , порядок 4 pq
Двойной	pq дуопирамида
Характеристики	выпуклый , вершинно-равномерный
Набор однородных пп дуопризм
Тип	Призматический однородный 4-многогранник
Символ Шлефли	{ п }×{ п }
Диаграмма Коксетера-Дынкина
Клетки	2 п п -угольные призмы
Лица	p 2 квадрата , 2 p p -угольника
Края	2 п 2
Вершины	стр 2
Симметрия	[ п ,2, п ] = [2 п ,2 + ,2 п ], порядок 8 п 2
Двойной	пп дуопирамида
Характеристики	выпуклый , вершинно-равномерный , фасетно-транзитивный

В геометрии 4 измерений или выше двойная призма ^[1] или дуопризма — это многогранник, полученный в результате декартова произведения двух многогранников, каждый из которых имеет два измерения или больше. Декартово произведение n-мерного многогранника и m-мерного многогранника — это ( n + m ) -мерный многогранник, где n и m — размерности 2 ( полигон ) или больше.

Дуопризмы наименьшей размерности существуют в 4-мерном пространстве как 4-многогранники, являющиеся декартовым произведением двух многоугольников в 2-мерном евклидовом пространстве . Точнее, это множество точек:

${\displaystyle P_{1}\times P_{2}=\{(x,y,z,w)|(x,y)\in P_{1},(z,w)\in P_{2}\}}$

где P ₁ и P ₂ — множества точек, содержащихся в соответствующих многоугольниках. Такая дуопризма является выпуклой , если оба основания выпуклые, и ограничена призматическими ячейками .

Четырехмерные дуопризмы считаются призматическими 4-многогранниками. Дуопризма, построенная из двух правильных многоугольников с одинаковой длиной ребра, является однородной дуопризмой .

Дуопризма, состоящая из n -полигонов и m -полигонов, называется путем добавления префикса «дуопризма» к именам базовых многоугольников, например: треугольно-пентагональная дуопризма является декартовым произведением треугольника и пятиугольника.

Альтернативный, более краткий способ указания конкретной дуопризмы — добавление к ней префиксов с числами, обозначающими базовые многоугольники, например: 3,5-дуопризма для треугольно-пентагональной дуопризмы.

Другие альтернативные названия:

• q -угольная- p -угольная призма
• q -угольная- p -угольная двойная призма
• q -гональная- p -гональная гиперпризма

Термин дуопризма был придуман Джорджем Ольшевским, сокращенно от double prism . Джон Хортон Конвей предложил похожее название пропризма для призмы произведения , декартова произведения двух или более многогранников размерности не менее двух. Дуопризмы — это пропризма, образованные ровно из двух многогранников.

Диаграмма Шлегеля Показаны проекции из центра одной 16-угольной призмы и всех, кроме одной, противоположных 16-угольных призм.

сеть Показаны два набора 16-угольных призм. Верхняя и нижняя грани вертикального цилиндра соединены при складывании в 4D.

4-мерная однородная дуопризма создается произведением правильного n -стороннего многоугольника и правильного m -стороннего многоугольника с одинаковой длиной ребра. Она ограничена n m -угольными призмами и m n -угольными призмами. Например, декартово произведение треугольника и шестиугольника является дуопризмой, ограниченной 6 треугольными призмами и 3 шестиугольными призмами.

• Когда m и n идентичны, результирующая дуопризма ограничена 2 n идентичными n -угольными призмами. Например, декартово произведение двух треугольников является дуопризмой, ограниченной 6 треугольными призмами.
• Когда m и n равны 4, результирующая дуопризма ограничена 8 квадратными призмами ( кубами ) и идентична тессеракту .

m - угольные призмы прикреплены друг к другу через свои m -угольные грани и образуют замкнутую петлю. Аналогично, n -угольные призмы прикреплены друг к другу через свои n -угольные грани и образуют вторую петлю, перпендикулярную первой. Эти две петли прикреплены друг к другу через свои квадратные грани и взаимно перпендикулярны.

Когда m и n стремятся к бесконечности, соответствующие дуопризмы приближаются к дуоцилиндру . Таким образом, дуопризмы полезны как неквадратичные приближения дуоцилиндра.

3-3
3-4	4-4
3-5	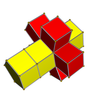4-5	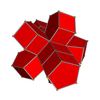5-5
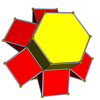3-6	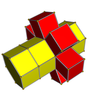4-6	5-6	6-6
3-7	4-7	5-7	6-7	7-7
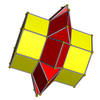3-8	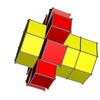4-8	5-8	6-8	7-8	8-8
3-9	4-9	5-9	6-9	7-9	8-9	9-9
3-10	4-10	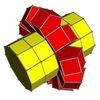5-10	6-10	7-10	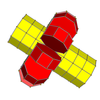8-10	9-10	10-10

Перспективная проекция с центром в ячейке делает дуопризму похожей на тор с двумя наборами ортогональных ячеек: p-угольными и q-угольными призмами.

Диаграммы Шлегеля

6-призма	6-6 дуопризма
Шестиугольная призма , спроецированная на плоскость с помощью перспективы, центрированная на шестиугольной грани, выглядит как двойной шестиугольник, соединенный (искаженными) квадратами . Аналогично 6-6 дуопризма, спроецированная в 3D, приближается к тору , шестиугольному как в плане, так и в сечении.

Дуопризмы pq идентичны дуопризмам qp, но выглядят по-разному в этих проекциях, поскольку они проецируются в центр разных ячеек.

Диаграммы Шлегеля

3-3	3-4	3-5	3-6	3-7	3-8
4-3	4-4	4-5	4-6	4-7	4-8
5-3	5-4	5-5	5-6	5-7	5-8
6-3	6-4	6-5	6-6	6-7	6-8
7-3	7-4	7-5	7-6	7-7	7-8
8-3	8-4	8-5	8-6	8-7	8-8

Вершинно-центрированные ортогональные проекции pp-дуопризм проецируются в симметрию [2n] для нечетных степеней и [n] для четных степеней. В центр проецируется n вершин. Для 4,4 это представляет плоскость Коксетера A ₃ тессеракта . Проекция 5,5 идентична трехмерному ромбическому триаконтаэдру .

Ортогональные проекционные каркасы пп-дуопризм

Странный
3-3			5-5			7-7			9-9
[3]		[6]	[5]		[10]	[7]		[14]	[9]		[18]
Даже
4-4 (тессеракт)			6-6			8-8			10-10
[4]		[8]	[6]		[12]	[8]		[16]	[10]		[20]

Правильный косой многогранник , {4,4|n}, существует в 4-мерном пространстве как n ² квадратных граней дуопризмы nn , использующей все 2n ² ребер и n ² вершин. 2 n n -угольных грани можно рассматривать как удаленные. (косые многогранники можно рассматривать таким же образом с помощью дуопризмы nm, но они не являются правильными .)

Подобно антипризмам как чередующимся призмам , существует набор 4-мерных дуоантипризм: 4-многогранников , которые могут быть созданы операцией чередования , примененной к дуопризме. Чередующиеся вершины создают нерегулярные тетраэдрические ячейки, за исключением особого случая, дуопризмы 4-4 ( тессеракта ), которая создает равномерную (и правильную) 16-ячейку . 16-ячейка является единственной выпуклой однородной дуоантипризмой.

Дуопризмы, t _0,1,2,3 {p,2,q}, можно заменить на, ht _0,1,2,3 {p,2,q}, "дуоантипризмы", которые не могут быть сделаны однородными в общем случае. Единственное выпуклое однородное решение - это тривиальный случай p=q=2, который является конструкцией тессеракта с более низкой симметрией , t _0,1,2,3 {2,2,2}, с его чередованием как 16-клеточный ,, с{2}с{2}.

Единственное невыпуклое равномерное решение — p=5, q=5/3, ht _0,1,2,3 {5,2,5/3},, построенный из 10 пентагональных антипризм , 10 пентаграммных скрещенных антипризм и 50 тетраэдров, известный как большая дуоантипризма (гудап). ^{[2] [3]}

Также родственны дитетраголтриаты или октаголтриаты, образованные взятием восьмиугольника ( считающегося дитетрагоном или усеченным квадратом) в p-угольник. Восьмиугольник p-угольника можно четко определить, если предположить, что восьмиугольник является выпуклой оболочкой двух перпендикулярных прямоугольников ; тогда p-угольный дитетраголтриат является выпуклой оболочкой двух pp дуопризм (где p-угольники подобны, но не конгруэнтны, имея разные размеры) в перпендикулярных ориентациях. Полученный полихор является изогональным и имеет 2p p-угольных призм и p ² прямоугольных трапеций ( куб с симметрией D _2d ), но не может быть сделан однородным. Вершинная фигура представляет собой треугольную бипирамиду .

Подобно дуоантипризмам как чередующимся дуопризмам, существует набор p-угольных двойных антипризмоидов, созданных чередованием 2p-угольных дитетраголтриатов, создающих p-угольные антипризмы и тетраэдры, при этом переосмысливая некореальмические треугольные бипирамидальные пространства как два тетраэдра. Полученная фигура, как правило, не является однородной, за исключением двух случаев: большой антипризмы и ее сопряженного пентаграммического двойного антипризмоида (с p = 5 и 5/3 соответственно), представленного как чередование декагонального или декаграммического дитетраголтриата. Вершинная фигура является вариантом сфенокороны .

Дуопризма 3-3 , -1 ₂₂ , является первой в размерной серии однородных многогранников, выраженной Коксетером как серия k _{22 . Дуопризма 3-3 является вершинной фигурой для второй,} двойного выпрямленного 5-симплекса . Четвертая фигура является евклидовыми сотами, 2 ₂₂ , а последняя - паракомпактными гиперболическими сотами, 3 ₂₂ , с группой Коксетера [3 ^2,2,3 ], . Каждый прогрессивный однородный многогранник строится из предыдущего как его вершинной фигуры .${\displaystyle {\bar {T}}_{7}}$

k ₂₂ фигур в n измерениях

Космос	Конечный			Евклидов	Гиперболический
н	4	5	6	7	8
Группа Коксетера	А 2 А 2	Е 6	${\displaystyle {\tilde {E}}_{6}}$=Э 6 +	${\displaystyle {\bar {T}}_{7}}$=Э 6 ++
Диаграмма Коксетера
Симметрия	[[3 2,2,-1 ]]	[[3 2,2,0 ]]	[[3 2,2,1 ]]	[[3 2,2,2 ]]	[[3 2,2,3 ]]
Заказ	72	1440	103,680	∞
График				∞	∞
Имя	−1 22	0 22	1 22	2 22	3 22

• Многогранник и 4-мерный многогранник
• Выпуклый правильный 4-мерный многогранник
• Дуоцилиндр
• Тессеракт

• Правильные многогранники , HSM Coxeter , Dover Publications, Inc., 1973, Нью-Йорк, стр. 124.
• Коксетер , Красота геометрии: Двенадцать эссе , Dover Publications, 1999, ISBN  0-486-40919-8 (Глава 5: Правильные косые многогранники в трех и четырех измерениях и их топологические аналоги)
  • Коксетер, HSM Правильные косые многогранники в трех и четырех измерениях. Труды London Math. Soc. 43, 33-62, 1937.
• Джон Х. Конвей , Хайди Берджил, Хаим Гудман-Штраус, Симметрии вещей 2008, ISBN 978-1-56881-220-5 (глава 26) 
• NW Johnson : Теория однородных многогранников и сот , докторская диссертация, Университет Торонто, 1966 г.