Мнимая единица

Мнимая единица или единичное мнимое число ( i ) является решением квадратного уравнения x ² + 1 = 0. Хотя не существует действительного числа с таким свойством, i можно использовать для расширения действительных чисел до так называемых комплексных чисел , используя сложение и умножение . Простой пример использования i в комплексном числе — 2 + 3 i .

Мнимые числа являются важным математическим понятием; они расширяют систему действительных чисел до комплексной системы чисел , в которой существует по крайней мере один корень для каждого непостоянного многочлена (см. Алгебраическое замыкание и Основная теорема алгебры ). Здесь термин «мнимый» используется, поскольку не существует действительного числа, имеющего отрицательный квадрат .${\displaystyle \mathbb {R} }$${\displaystyle \mathbb {C} ,}$

Существует два комплексных квадратных корня из −1: i и − i , так же как существует два комплексных квадратных корня из каждого действительного числа, кроме нуля (который имеет один двойной квадратный корень ).

В контекстах, в которых использование буквы i неоднозначно или проблематично, иногда вместо нее используется буква j . Например, в электротехнике и проектировании систем управления мнимая единица обычно обозначается как j вместо i , поскольку i обычно используется для обозначения электрического тока . ^[1]

Квадратные корни из отрицательных чисел называются мнимыми , потому что в ранней современной математике только то, что сейчас называется действительными числами , получаемыми с помощью физических измерений или базовой арифметики, считалось числами вообще — даже к отрицательным числам относились скептически — поэтому квадратный корень из отрицательного числа ранее считался неопределенным или бессмысленным. Название мнимый обычно приписывают Рене Декарту , а Исаак Ньютон использовал этот термин еще в 1670 году. ^{[2] [3]} Обозначение i было введено Леонардом Эйлером . ^[4]

Единица — это неделимое целое, а единица или число единицы — это число один ( 1 ).

Степени i являются циклическими:
${\displaystyle \ \vdots }$
${\displaystyle \ i^{-4}={\phantom {-}}1{\phantom {i}}}$
${\displaystyle \ i^{-3}={\phantom {-}}i{\phantom {1}}}$
${\displaystyle \ i^{-2}=-1{\phantom {i}}}$
${\displaystyle \ i^{-1}=-i{\phantom {1}}}$
${\displaystyle \ \ i^{0}\ ={\phantom {-}}1{\phantom {i}}}$
${\displaystyle \ \ i^{1}\ ={\phantom {-}}i{\phantom {1}}}$
${\displaystyle \ \ i^{2}\ =-1{\phantom {i}}}$
${\displaystyle \ \ i^{3}\ =-i{\phantom {1}}}$
${\displaystyle \ \ i^{4}\ ={\phantom {-}}1{\phantom {i}}}$
${\displaystyle \ \ i^{5}\ ={\phantom {-}}i{\phantom {1}}}$
${\displaystyle \ \ i^{6}\ =-1{\phantom {i}}}$
${\displaystyle \ \ i^{7}\ =-i{\phantom {1}}}$
${\displaystyle \ \vdots }$

Мнимая единица i определяется исключительно тем свойством, что ее квадрат равен −1:$${\displaystyle i^{2}=-1.}$$

Если i определить таким образом, то из алгебры непосредственно следует , что i и − i являются квадратными корнями из −1.

Хотя конструкция называется «мнимой», и хотя концепция мнимого числа может быть интуитивно более трудной для понимания, чем концепция действительного числа, конструкция верна с математической точки зрения. Операции с действительными числами можно распространить на мнимые и комплексные числа, рассматривая i как неизвестную величину при манипулировании выражением (и используя определение для замены любого вхождения i ² на −1 ). Высшие целые степени i — это, таким образом , и так далее, циклически проходя через четыре значения 1 , i , −1 и − i . Как и в случае с любым ненулевым действительным числом, i ⁰ = 1.$${\displaystyle {\begin{alignedat}{3}i^{3}&=i^{2}i&&=(-1)i&&=-i,\\[3mu]i^{4}&=i^{3}i&&=\;\!(-i)i&&=\ \,1,\\[3mu]i^{5}&=i^{4}i&&=\ \,(1)i&&=\ \ i,\end{alignedat}}}$$

Как комплексное число, i может быть представлено в прямоугольной форме как 0 + 1 i , с нулевым действительным компонентом и единичным мнимым компонентом. В полярной форме i может быть представлено как 1 × e ^{πi /2} (или просто e ^{πi /2} ), с абсолютным значением (или величиной) 1 и аргументом (или углом) радиан . (Добавление любого целого числа, кратного 2 π, к этому углу также работает.) В комплексной плоскости , которая является специальной интерпретацией декартовой плоскости , i является точкой, расположенной на одну единицу от начала координат вдоль мнимой оси (которая ортогональна действительной оси ).${\displaystyle {\tfrac {\pi }{2}}}$

Будучи квадратным многочленом без кратных корней , определяющее уравнение x ² = −1 имеет два различных решения, которые одинаково допустимы и которые являются аддитивными и мультипликативными обратными друг другу. Хотя два решения являются различными числами, их свойства неразличимы; нет такого свойства, которым обладало бы одно из них, но не обладало бы другое. Одно из этих двух решений обозначено как + i (или просто i ), а другое обозначено как − i , хотя по сути неоднозначно, какое из них какое.

Единственные различия между + i и − i возникают из-за этой маркировки. Например, по соглашению говорят, что + i имеет аргумент , а − i имеет аргумент, связанный с соглашением о маркировке ориентаций в декартовой плоскости относительно положительной оси x с положительными углами, поворачивающимися против часовой стрелки в направлении положительной оси y . Кроме того, несмотря на знаки, написанные с ними, ни + i, ни − i не являются изначально положительными или отрицательными в том смысле, в каком являются действительные числа. ^[5]${\displaystyle +{\tfrac {\pi }{2}}}$${\displaystyle -{\tfrac {\pi }{2}},}$

Более формальное выражение этой неразличимости + i и − i заключается в том, что, хотя комплексное поле уникально (как расширение действительных чисел) с точностью до изоморфизма , оно не уникально с точностью до единственного изоморфизма. То есть, существуют два полевых автоморфизма комплексных чисел , которые сохраняют каждое действительное число фиксированным, а именно тождество и комплексное сопряжение . Подробнее об этом общем явлении см. Группа Галуа . ${\displaystyle \mathbb {C} }$

Используя концепции матриц и умножения матриц , комплексные числа могут быть представлены в линейной алгебре. Действительная единица 1 и мнимая единица i могут быть представлены любой парой матриц I и J, удовлетворяющих соотношениям I ² = I , IJ = JI = J и J ² = − I . Тогда комплексное число a + bi может быть представлено матрицей aI + bJ , и все обычные правила комплексной арифметики могут быть выведены из правил матричной арифметики.

Наиболее распространенным выбором является представление 1 и i с помощью единичной матрицы I размером 2 × 2 и матрицы J ,

$${\displaystyle I={\begin{pmatrix}1&0\\0&1\end{pmatrix}},\quad J={\begin{pmatrix}0&-1\\1&0\end{pmatrix}}.}$$

Тогда произвольное комплексное число a + bi можно представить в виде:

$${\displaystyle aI+bJ={\begin{pmatrix}a&-b\\b&a\end{pmatrix}}.}$$

В более общем случае любая вещественная матрица 2 × 2 со следом , равным нулю, и определителем , равным единице в квадрате, равная − I , может быть выбрана для J. Также могут использоваться матрицы большего размера; например, 1 может быть представлена ​​единичной матрицей 4 × 4 , а i может быть представлена ​​любой из матриц Дирака для пространственных измерений.

Многочлены (взвешенные суммы степеней переменной) являются основным инструментом в алгебре. Многочлены, коэффициенты которых являются действительными числами, образуют кольцо , обозначаемое как алгебраическая структура со сложением и умножением и разделяющее многие свойства с кольцом целых чисел .${\displaystyle \mathbb {R} [x],}$

Многочлен не имеет действительных корней , но множество всех действительных многочленов, делящихся на, образует идеал , и поэтому существует фактор-кольцо Это фактор-кольцо изоморфно комплексным числам, а переменная выражает мнимую единицу.${\displaystyle x^{2}+1}$${\displaystyle x^{2}+1}$ ${\displaystyle \mathbb {R} [x]/\langle x^{2}+1\rangle .}$${\displaystyle x}$

Комплексные числа можно представить графически, изобразив прямую действительных чисел как горизонтальную ось, а мнимые числа как вертикальную ось декартовой плоскости, называемой комплексной плоскостью . В этом представлении числа 1 и i находятся на одинаковом расстоянии от 0 , с прямым углом между ними. Сложение с комплексным числом соответствует переносу в плоскости, тогда как умножение на комплексное число единичной величины соответствует вращению вокруг начала координат. Каждое преобразование подобия плоскости можно представить комплексно-линейной функцией${\displaystyle z\mapsto az+b.}$

В геометрической алгебре евклидовой плоскости геометрическое произведение или частное двух произвольных векторов представляет собой сумму скалярной (действительной) части и бивекторной части. (Скаляр — это величина без ориентации, вектор — это величина, ориентированная подобно линии, а бивектор — это величина, ориентированная подобно плоскости.) Квадрат любого вектора является положительным скаляром, представляющим квадрат его длины, в то время как квадрат любого бивектора является отрицательным скаляром.

Частное вектора с самим собой — это скаляр 1 = u / u , и при умножении на любой вектор оставляет его неизменным ( тождественное преобразование ). Частное любых двух перпендикулярных векторов одинаковой величины, J = u / v , которое при умножении поворачивает делитель на четверть оборота в делимое, Jv = u , является единичным бивектором, который возводится в квадрат до −1 , и, таким образом, может быть взято в качестве представителя мнимой единицы. Любая сумма скаляра и бивектора может быть умножена на вектор для его масштабирования и поворота, и алгебра таких сумм изоморфна алгебре комплексных чисел. В этой интерпретации точки, векторы и суммы скаляров и бивекторов являются различными типами геометрических объектов. ^[6]

В более общем смысле, в геометрической алгебре любого многомерного евклидова пространства единичный бивектор любой произвольной плоской ориентации имеет квадрат, равный −1 , поэтому его можно рассматривать как представляющий мнимую единицу i .

Мнимая единица исторически была написана и все еще используется в некоторых современных работах. Однако, необходимо проявлять большую осторожность при манипулировании формулами, включающими радикалы . Обозначение знака радикала зарезервировано либо для главной функции квадратного корня, которая определена только для вещественного x ≥ 0, либо для главной ветви комплексной функции квадратного корня. Попытка применить правила вычисления главной (вещественной) функции квадратного корня для манипулирования главной ветвью комплексной функции квадратного корня может привести к ложным результатам: ^[7]${\textstyle {\sqrt {-1}},}$${\textstyle {\sqrt {x}}}$$${\displaystyle -1=i\cdot i={\sqrt {-1}}\cdot {\sqrt {-1}}\mathrel {\stackrel {\mathrm {fallacy} }{=}} {\textstyle {\sqrt {(-1)\cdot (-1)}}}={\sqrt {1}}=1\qquad {\text{(incorrect).}}}$$

Как правило, правила расчета и гарантированно действительны только для действительных положительных значений x и y . ^{[8] [9] [10]}${\textstyle {\sqrt {x{\vphantom {ty}}}}\cdot \!{\sqrt {y{\vphantom {ty}}}}={\sqrt {x\cdot y{\vphantom {ty}}}}}$${\textstyle {\sqrt {x{\vphantom {ty}}}}{\big /}\!{\sqrt {y{\vphantom {ty}}}}={\sqrt {x/y}}}$

Когда x или y действительны, но отрицательны, этих проблем можно избежать, записывая и манипулируя выражениями типа , а не . Более подробное обсуждение см. в статьях Квадратный корень и Точка ветвления .${\textstyle i{\sqrt {7}}}$${\textstyle {\sqrt {-7}}}$

Как комплексное число, мнимая единица подчиняется всем правилам комплексной арифметики .

При многократном добавлении или вычитании мнимой единицы результатом является некоторое целое число , умноженное на мнимую единицу, т. е. мнимое целое число ; любые такие числа можно сложить, и результатом также будет мнимое целое число:

$${\displaystyle ai+bi=(a+b)i.}$$

Таким образом, мнимая единица является генератором группы по сложению, а именно бесконечной циклической группы .

Мнимую единицу также можно умножить на любое произвольное действительное число , чтобы получить мнимое число . Эти числа можно изобразить на числовой прямой , мнимой оси , которая как часть комплексной плоскости обычно рисуется с вертикальной ориентацией, перпендикулярной действительной оси, которая рисуется горизонтально.

Целочисленные суммы действительной единицы 1 и мнимой единицы i образуют квадратную решетку в комплексной плоскости, называемую гауссовыми целыми числами . Сумма, разность или произведение гауссовых целых чисел также является гауссовым целым числом:

$${\displaystyle {\begin{aligned}(a+bi)+(c+di)&=(a+c)+(b+d)i,\\[5mu](a+bi)(c+di)&=(ac-bd)+(ad+bc)i.\end{aligned}}}$$

При умножении на мнимую единицу i любое произвольное комплексное число в комплексной плоскости поворачивается на четверть оборота ( радианы${\displaystyle {\tfrac {1}{2}}\pi }$ или 90° ) против часовой стрелки . При умножении на − i любое произвольное комплексное число поворачивается на четверть оборота по часовой стрелке. В полярной форме:

$${\displaystyle i\,re^{\varphi i}=re^{(\varphi +\pi /2)i},\quad -i\,re^{\varphi i}=re^{(\varphi -\pi /2)i}.}$$

В прямоугольной форме,

$${\displaystyle i(a+bi)=-b+ai,\quad -i(a+bi)=b-ai.}$$

Степени i повторяются в цикле, который можно выразить с помощью следующего шаблона, где n — любое целое число:

$${\displaystyle i^{4n}=1,\quad i^{4n+1}=i,\quad i^{4n+2}=-1,\quad i^{4n+3}=-i.}$$

Таким образом, при умножении i является генератором циклической группы порядка 4, дискретной подгруппы непрерывной круговой группы единичных комплексных чисел при умножении.

Записано как частный случай формулы Эйлера для целого числа n :

$${\displaystyle i^{n}={\exp }{\bigl (}{\tfrac {1}{2}}\pi i{\bigr )}^{n}={\exp }{\bigl (}{\tfrac {1}{2}}n\pi i{\bigr )}={\cos }{\bigl (}{\tfrac {1}{2}}n\pi {\bigr )}+{i\sin }{\bigl (}{\tfrac {1}{2}}n\pi {\bigr )}.}$$

При тщательном выборе ветвей и главных значений это последнее уравнение может также применяться к произвольным комплексным значениям n , включая такие случаи, как n = i . ^{[ требуется ссылка ]}

Как и все ненулевые комплексные числа, имеет два различных квадратных корня , которые являются аддитивными обратными . В полярной форме они${\textstyle i=e^{\pi i/2}}$$${\displaystyle {\begin{alignedat}{3}{\sqrt {i}}&={\exp }{\bigl (}{\tfrac {1}{2}}{\pi i}{\bigr )}^{1/2}&&{}={\exp }{\bigl (}{\tfrac {1}{4}}\pi i{\bigr )},\\-{\sqrt {i}}&={\exp }{\bigl (}{\tfrac {1}{4}}{\pi i}-\pi i{\bigr )}&&{}={\exp }{\bigl (}{-{\tfrac {3}{4}}\pi i}{\bigr )}.\end{alignedat}}}$$

В прямоугольной форме они ^[a]

$${\displaystyle {\begin{alignedat}{3}{\sqrt {i}}&=\ (1+i){\big /}{\sqrt {2}}&&{}={\phantom {-}}{\tfrac {\sqrt {2}}{2}}+{\tfrac {\sqrt {2}}{2}}i,\\[5mu]-{\sqrt {i}}&=-(1+i){\big /}{\sqrt {2}}&&{}=-{\tfrac {\sqrt {2}}{2}}-{\tfrac {\sqrt {2}}{2}}i.\end{alignedat}}}$$

Возведение любого выражения в квадрат дает$${\displaystyle \left(\pm {\frac {1+i}{\sqrt {2}}}\right)^{2}={\frac {1+2i-1}{2}}={\frac {2i}{2}}=i.}$$

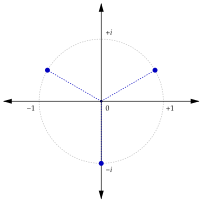
Три кубических корня из i равны ^[12]

$${\displaystyle {\sqrt[{3}]{i}}={\exp }{\bigl (}{\tfrac {1}{6}}\pi i{\bigr )}={\tfrac {\sqrt {3}}{2}}+{\tfrac {1}{2}}i,\quad {\exp }{\bigl (}{\tfrac {5}{6}}\pi i{\bigr )}=-{\tfrac {\sqrt {3}}{2}}+{\tfrac {1}{2}}i,\quad {\exp }{\bigl (}{-{\tfrac {1}{2}}\pi i}{\bigr )}=-i.}$$

Для общего положительного целого числа n корни степени n из i равны, для k = 0, 1, ..., n − 1, Значение, связанное с k = 0, является главным корнем степени n из i . Набор корней равен соответствующему набору корней из единицы, повернутых главным корнем степени n из i . Это вершины правильного многоугольника , вписанного в комплексную единичную окружность .$${\displaystyle \exp \left(2\pi i{\frac {k+{\frac {1}{4}}}{n}}\right)=\cos \left({\frac {4k+1}{2n}}\pi \right)+i\sin \left({\frac {4k+1}{2n}}\pi \right).}$$

Комплексная экспоненциальная функция связывает комплексное сложение в области с комплексным умножением в кодомене. Действительные значения в области представляют масштабирование в кодомене (умножение на действительный скаляр), где 1 представляет умножение на e , в то время как мнимые значения в области представляют вращение в кодомене (умножение на единичное комплексное число), где i представляет вращение на 1 радиан. Таким образом, комплексная экспонента является периодической функцией в мнимом направлении с периодом 2 πi и изображением 1 в точках 2 kπi для всех целых чисел k , действительным кратным решетки мнимых целых чисел.

Комплексную экспоненту можно разбить на четные и нечетные компоненты, гиперболические функции cosh и sinh или тригонометрические функции cos и sin :

$${\displaystyle \exp z=\cosh z+\sinh z=\cos(-iz)+i\sin(-iz)}$$

Формула Эйлера раскладывает экспоненту мнимого числа, представляющего поворот:

$${\displaystyle \exp i\varphi =\cos \varphi +i\sin \varphi .}$$

Этот факт можно использовать, помимо прочего, для демонстрации, по-видимому, противоречащего интуиции результата, который является действительным числом. ^[13]${\displaystyle i^{i}}$

Частное coth z = cosh z / sinh z при соответствующем масштабировании можно представить в виде разложения бесконечной дроби как суммы обратных функций, преобразованных в мнимые целые числа: ^[14]$${\displaystyle \pi \coth \pi z=\lim _{n\to \infty }\sum _{k=-n}^{n}{\frac {1}{z+ki}}.}$$

Другие функции, основанные на комплексной экспоненте, хорошо определены с мнимыми входами. Например, число, возведенное в степень ni, равно:$${\displaystyle x^{ni}=\cos(n\ln x)+i\sin(n\ln x).}$$

Поскольку экспонента является периодической, ее обратная функция комплексный логарифм является многозначной функцией , причем каждое комплексное число в области соответствует нескольким значениям в области значений, отделенным друг от друга любым целым числом, кратным 2 πi . Один из способов получения однозначной функции — рассматривать область значений как цилиндр , а комплексные значения, разделенные любым целым числом, кратным 2 πi, рассматривать как одно и то же значение; другой способ — взять область значений как риманову поверхность, состоящую из нескольких копий комплексной плоскости, сшитых вместе вдоль отрицательной действительной оси как разрез ветви , причем каждая ветвь в области значений соответствует одной бесконечной полосе в области значений. ^[15] Функции, зависящие от комплексного логарифма, поэтому зависят от тщательного выбора ветви для четкого определения и оценки.

Например, если выбрать любую ветвь, то когда x — положительное действительное число,${\displaystyle \ln i={\tfrac {1}{2}}\pi i}$$${\displaystyle \log _{i}x=-{\frac {2i\ln x}{\pi }}.}$$

Факториал мнимой единицы i чаще всего задается в терминах гамма-функции, оцененной по формуле 1 + i : ^[16]

$${\displaystyle i!=\Gamma (1+i)=i\Gamma (i)\approx 0.4980-0.1549\,i.}$$

Величина и аргумент этого числа таковы: ^[17]

$${\displaystyle |\Gamma (1+i)|={\sqrt {\frac {\pi }{\sinh \pi }}}\approx 0.5216,\quad \arg {\Gamma (1+i)}\approx -0.3016.}$$

• Гиперболическая единица
• Правый версор в кватернионах

• Нахин, Пол Дж. (1998). Воображаемая история: История i [квадратный корень из минус единицы] . Чичестер: Princeton University Press. ISBN 0-691-02795-1– через Archive.org.

• Эйлер, Леонард . "Мнимые корни многочленов". Архивировано из оригинала 16 декабря 2019 г. Получено 29 ноября 2012 г.в "Convergence". mathdl.maa.org . Математическая ассоциация Америки. Архивировано из оригинала 13 июля 2007 г.