Золотое сечение
 | |
| Представления | |
|---|---|
| Десятичная дробь | 1.618 033 988 749 894 ... [1] |
| Алгебраическая форма | |
| Продолженная дробь | |

В математике две величины находятся в золотом сечении , если их отношение равно отношению их суммы к большей из двух величин. Выражаясь алгебраически, для величин и с , находится в золотом сечении к , если
где греческая буква фи ( или ) обозначает золотое сечение. [a] Константа удовлетворяет квадратному уравнению и является иррациональным числом со значением [1]
Золотое сечение было названо Евклидом крайним и средним отношением [2], а Лукой Пачоли — божественной пропорцией [3] , а также имеет другие названия. [b]
Математики изучали свойства золотого сечения с древних времен. Это отношение диагонали правильного пятиугольника к его стороне и, таким образом, появляется в конструкции додекаэдра и икосаэдра . [7] Золотой прямоугольник — то есть прямоугольник с соотношением сторон — можно разрезать на квадрат и меньший прямоугольник с тем же соотношением сторон . Золотое сечение использовалось для анализа пропорций природных объектов и искусственных систем, таких как финансовые рынки , в некоторых случаях на основе сомнительных подгонок к данным. [8] Золотое сечение появляется в некоторых узорах в природе , включая спиральное расположение листьев и других частей растительности.
Некоторые художники и архитекторы 20-го века , включая Ле Корбюзье и Сальвадора Дали , пропорционировали свои работы, приближаясь к золотому сечению, полагая, что это эстетически приятно. Эти применения часто появляются в форме золотого прямоугольника.
Расчет
Две величины и находятся в золотом отношении, если [9]
Один из методов нахождения замкнутой формы для начинается с левой дроби. Упрощая дробь и подставляя обратную ,
Поэтому,
Умножение на дает
который можно переставить на
Квадратичная формула дает два решения:
Поскольку это отношение между положительными величинами, то это обязательно положительный корень. [10] Отрицательный корень на самом деле является отрицательным обратным сечением , которое имеет много общих свойств с золотым сечением.
История
По словам Марио Ливио ,
Некоторые из величайших математических умов всех времен, от Пифагора и Евклида в Древней Греции , через средневекового итальянского математика Леонардо Пизанского и астронома эпохи Возрождения Иоганна Кеплера , до современных научных деятелей, таких как оксфордский физик Роджер Пенроуз , проводили бесконечные часы над этим простым соотношением и его свойствами. ... Биологи, художники, музыканты, историки, архитекторы, психологи и даже мистики размышляли и обсуждали основу его повсеместности и привлекательности. Фактически, вероятно, справедливо будет сказать, что Золотое сечение вдохновило мыслителей всех дисциплин, как никакое другое число в истории математики. [11]
— Золотое сечение: история Фи, самого удивительного числа в мире
Древнегреческие математики впервые изучили золотое сечение из-за его частого появления в геометрии ; [12] деление линии на «крайнее и среднее отношение» (золотое сечение) важно в геометрии правильных пентаграмм и пятиугольников . [13] Согласно одной истории, математик V века до н. э. Гиппас обнаружил, что золотое сечение не является ни целым числом, ни дробью (оно иррационально ), что удивило пифагорейцев . [14] « Начала » Евклида ( ок. 300 г. до н. э. ) содержат несколько утверждений и их доказательств, использующих золотое сечение, [15] [c] и содержат его первое известное определение, которое выглядит следующим образом: [16]
Говорят, что прямая линия разрезана в крайнем и среднем отношении, когда, как вся линия относится к большему сегменту, так и больший сегмент относится к меньшему. [17] [d]

Золотое сечение изучалось периферийно в течение следующего тысячелетия. Абу Камиль (ок. 850–930) использовал его в своих геометрических расчетах пятиугольников и десятиугольников; его труды оказали влияние на Фибоначчи (Леонардо Пизанский) (ок. 1170–1250), который использовал это соотношение в смежных геометрических задачах, но не заметил, что оно связано с числами Фибоначчи . [19]
Лука Пачоли назвал свою книгу Divina ratio ( 1509 ) в честь пропорции; книга, в значительной степени плагиат у Пьеро делла Франческа , исследовала ее свойства, включая ее появление в некоторых Платоновых телах . [20] [21] Леонардо да Винчи , который иллюстрировал книгу Пачоли, назвал пропорцию sectio aurea («золотое сечение»). [22] Хотя часто говорят, что Пачоли выступал за применение золотого сечения для получения приятных, гармоничных пропорций, Ливио указывает, что интерпретация была прослежена до ошибки в 1799 году, и что Пачоли на самом деле выступал за витрувианскую систему рациональных пропорций. [23] Пачоли также видел католическое религиозное значение в пропорции, что и привело к названию его работы. Математики 16-го века, такие как Рафаэль Бомбелли, решали геометрические задачи, используя пропорцию. [24]
Немецкий математик Симон Якоб (ум. 1564) заметил, что последовательные числа Фибоначчи сходятся к золотому сечению; [25] это было заново открыто Иоганном Кеплером в 1608 году. [26] Первое известное десятичное приближение (обратного) золотого сечения было указано как «около » в 1597 году Михаэлем Местлином из Тюбингенского университета в письме Кеплеру, его бывшему ученику. [27] В том же году Кеплер написал Местлину о треугольнике Кеплера , который объединяет золотое сечение с теоремой Пифагора . Кеплер сказал о них:
Геометрия имеет два великих сокровища: одно — теорема Пифагора, другое — деление линии в крайнем и среднем отношении. Первое мы можем сравнить с массой золота, второе мы можем назвать драгоценным камнем. [28]
Математики восемнадцатого века Авраам де Муавр , Николай I Бернулли и Леонард Эйлер использовали формулу на основе золотого сечения, которая находит значение числа Фибоначчи на основе его положения в последовательности; в 1843 году это было заново открыто Жаком Филиппом Мари Бине , в честь которого она была названа «формулой Бине». [29] Мартин Ом впервые использовал немецкий термин goldener Schnitt («золотое сечение») для описания соотношения в 1835 году. [30] Джеймс Салли использовал эквивалентный английский термин в 1875 году. [31]
К 1910 году изобретатель Марк Барр начал использовать греческую букву фи ( ) в качестве символа золотого сечения. [32] [e] Она также была представлена тау ( ), первой буквой древнегреческого τομή («разрез» или «сечение»). [35]

Система построения zome , разработанная Стивом Бэром в конце 1960-х годов, основана на системе симметрии икосаэдра / додекаэдра и повсеместно использует золотое сечение. Между 1973 и 1974 годами Роджер Пенроуз разработал мозаику Пенроуза , узор, связанный с золотым сечением как по соотношению площадей его двух ромбических плиток, так и по их относительной частоте в узоре. [36] Это привлекло внимание после открытия Дэном Шехтманом в 1982 году квазикристаллов с икосаэдрической симметрией, которые вскоре были объяснены посредством аналогий с мозаикой Пенроуза. [37]
Математика
Иррациональность
Золотое сечение — иррациональное число . Ниже приведены два коротких доказательства иррациональности:
Противоречие из выражения в самых низких терминах

Это доказательство бесконечным спуском . Напомним, что:
целое относится к более длинной части так же, как более длинная часть относится к более короткой.
Если мы назовем целое и более длинную часть , то второе утверждение выше становится
Сказать, что золотое сечение рационально, означает, что это дробь , где и — целые числа. Мы можем считать, что находится в наименьших числах , а и — положительные. Но если находится в наименьших числах, то равнозначное находится в ещё меньших числах. Это противоречие, вытекающее из предположения, что является рациональным.
По иррациональности√ 5
Другое короткое доказательство — возможно, более известное — иррациональности золотого сечения использует замыкание рациональных чисел относительно сложения и умножения. Если рационально, то также рационально, что является противоречием, если уже известно, что квадратные корни всех неквадратных натуральных чисел иррациональны.
Минимальный многочлен
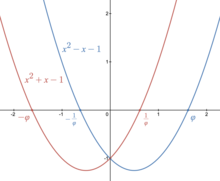
Золотое сечение также является алгебраическим числом и даже алгебраическим целым числом . Оно имеет минимальный многочлен
Этот квадратный многочлен имеет два корня , и
Золотое сечение также тесно связано с многочленом
который имеет корни и Как корень квадратного многочлена, золотое сечение является конструируемым числом . [38]
Золотое сечение сопряженное и степени
Сопряженный корень минимального многочлена равен
Абсолютное значение этой величины ( ) соответствует отношению длин, взятому в обратном порядке (длина более короткого сегмента к длине более длинного сегмента, ).
Это иллюстрирует уникальное свойство золотого сечения среди положительных чисел, а именно:
или его обратная формула:
Сопряженное и определяющее квадратичное полиномиальное отношение приводят к десятичным значениям, имеющим общую дробную часть с :
Последовательность степеней содержит следующие значения. В более общем случае любая степень равна сумме двух непосредственно предшествующих степеней:
В результате можно легко разложить любую степень на кратное и константу. Кратное и константа всегда являются соседними числами Фибоначчи. Это приводит к другому свойству положительных степеней :
Если тогда:
Цепная дробь и квадратный корень

Формулу можно рекурсивно расширить, чтобы получить простую цепную дробь для золотого сечения: [39]
На самом деле это простейшая форма цепной дроби, наряду с ее обратной формой:
Конвергенты этих непрерывных дробей ( ... или ...) являются отношениями последовательных чисел Фибоначчи . Постоянно малые члены в ее непрерывной дроби объясняют, почему аппроксиманты сходятся так медленно. Это делает золотое сечение предельным случаем неравенства Гурвица для диофантовых приближений , которое утверждает, что для каждого иррационального числа существует бесконечно много различных дробей, таких что,
Это означает, что константу нельзя улучшить, не исключив золотое сечение. Это, по сути, наименьшее число, которое должно быть исключено для получения более точных приближений таких чисел Лагранжа . [40]
Продолжение квадратного корня для можно получить из , что даёт: [41]
Связь с числами Фибоначчи и Люка
Числа Фибоначчи и числа Люка имеют сложную связь с золотым сечением. В последовательности Фибоначчи каждое число равно сумме двух предыдущих, начиная с базовой последовательности :
Последовательность чисел Люка (не путать с обобщенными последовательностями Люка , частью которых является эта) похожа на последовательность Фибоначчи, в которой каждый член является суммой двух предыдущих, однако вместо этого начинается с :
В исключительном случае золотое сечение равно пределу отношений последовательных членов в последовательности Фибоначчи и последовательности чисел Люка: [42]
Другими словами, если число Фибоначчи и Люка разделить на его непосредственное предшественника в последовательности, то частное приблизительно равно .
Например, и
Эти приближения попеременно то ниже, то выше и сходятся к значению по мере увеличения чисел Фибоначчи и Люка.
Закрытые выражения для последовательностей Фибоначчи и Люка, включающие золотое сечение, следующие:
Объединив обе приведенные выше формулы, получаем формулу , которая включает как числа Фибоначчи, так и числа Люка:
Между числами Фибоначчи и числами Люка можно сделать вывод , который упрощает выражение предела частного чисел Люка по числам Фибоначчи как равного квадратному корню из пяти :
На самом деле, верны гораздо более сильные утверждения:
Эти значения описываются как фундаментальная единица алгебраического числового поля .
Последовательные степени золотого сечения подчиняются закону Фибоначчи , т.е.
Приведение к линейному выражению можно осуществить за один шаг, используя:
Это тождество позволяет свести любой многочлен к линейному выражению, например:
Последовательные числа Фибоначчи также можно использовать для получения аналогичной формулы для золотого сечения, здесь путем бесконечного суммирования :
В частности, степени самих себя округляются до чисел Лукаса (по порядку, за исключением первых двух степеней, и , которые расположены в обратном порядке):
и т. д. [43] Числа Лукаса также напрямую генерируют степени золотого сечения; для :
В основе их взаимосвязанной связи с золотым сечением лежит представление о том, что сумма третьих последовательных чисел Фибоначчи равна числу Лукаса, то есть ; и, что важно, .
Как последовательность Фибоначчи, так и последовательность чисел Люка могут быть использованы для создания приблизительных форм золотой спирали (которая является особой формой логарифмической спирали ) с использованием четвертей окружностей с радиусами из этих последовательностей, лишь немного отличающимися от истинной золотой логарифмической спирали. Спираль Фибоначчи — это, как правило, термин, используемый для спиралей, которые приближают золотые спирали с помощью квадратов и четвертей окружностей, упорядоченных числами Фибоначчи.
Геометрия
Золотое сечение играет важную роль в геометрии. Например, оно неотъемлемо вовлечено во внутреннюю симметрию пентагона и распространяется, образуя часть координат вершин правильного додекаэдра , а также 5-ячейников . Оно также присутствует в треугольнике Кеплера и мозаиках Пенроуза , а также в различных других многогранниках .
Строительство
Деление внутренним делением
- Имея отрезок прямой, построить перпендикуляр в точке с половиной длины Начертить гипотенузу
- Начертите дугу с центром и радиусом. Эта дуга пересекает гипотенузу в точке
- Начертите дугу с центром и радиусом. Эта дуга пересекает исходный отрезок прямой в точке Точка делит исходный отрезок прямой на отрезки с длинами в золотом сечении.
Деление внешним делением
- Начертите отрезок прямой и постройте из этой точки отрезок, перпендикулярный прямой и имеющий ту же длину, что и
- Разделите отрезок пополам с помощью
- Дуга окружности с радиусом пересекает в точке прямую, проходящую через точки и (также известную как продолжение ). Отношение к построенному отрезку является золотым сечением.
Примеры применения вы можете увидеть в статьях Пятиугольник с заданной длиной стороны , Десятиугольник с заданной описанной окружностью и Десятиугольник с заданной длиной стороны .
Оба представленных выше различных алгоритма создают геометрические конструкции , определяющие два выровненных отрезка , где отношение более длинного из них к более короткому является золотым сечением.
Золотой угол

Когда два угла, образующие полный круг, имеют пропорции золотого сечения, меньший из них называется золотым углом , с мерой
Этот угол встречается в моделях роста растений как оптимальное расстояние между побегами листьев вокруг стеблей растений, так что последующие листья не блокируют солнечный свет от листьев, расположенных ниже. [44]
Пятиугольная система симметрии
Пентагон и пентаграмма

В правильном пятиугольнике отношение диагонали к стороне является золотым сечением, в то время как пересекающиеся диагонали секут друг друга в золотом сечении. Свойства золотого сечения правильного пятиугольника можно подтвердить, применив теорему Птолемея к четырехугольнику, образованному удалением одной из его вершин. Если длинное ребро и диагонали четырехугольника равны , а короткие ребра равны , то теорема Птолемея дает Разделив обе стороны на получаем (см. § Расчет выше),
Диагональные сегменты пятиугольника образуют пентаграмму , или пятиконечный звездный многоугольник , геометрия которого по сути описывается . В первую очередь, каждое пересечение ребер секёт другие ребра в золотом сечении. Отношение длины более короткого сегмента к сегменту, ограниченному двумя пересекающимися ребрами (то есть стороной перевёрнутого пятиугольника в центре пентаграммы), такое, как показано на четырёхцветной иллюстрации.
Пятиугольная и пентаграммная геометрия позволяет нам вычислить следующие значения для :
Золотой треугольник и золотой гномон
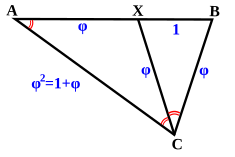
Треугольник, образованный двумя диагоналями и стороной правильного пятиугольника, называется золотым треугольником или возвышенным треугольником . Это остроугольный равнобедренный треугольник с углом при вершине 36° и углами при основании 72°. [45] Его две равные стороны находятся в золотом отношении к его основанию. [46] Треугольник, образованный двумя сторонами и диагональю правильного пятиугольника, называется золотым гномоном . Это тупоугольный равнобедренный треугольник с углом при вершине 108° и углом при основании 36°. Его основание находится в золотом отношении к его двум равным сторонам. [46] Таким образом, пятиугольник можно разделить на два золотых гномона и центральный золотой треугольник. Пять вершин правильной пентаграммы являются золотыми треугольниками, [46] как и десять треугольников, образованных соединением вершин правильного десятиугольника с его центральной точкой. [47]
Бисекция одного из углов основания золотого треугольника подразделяет его на меньший золотой треугольник и золотой гномон. Аналогично, любой остроугольный равнобедренный треугольник может быть подразделен на подобный треугольник и тупоугольный равнобедренный треугольник, но золотой треугольник является единственным, для которого это подразделение выполняется биссектрисой угла, потому что это единственный равнобедренный треугольник, угол основания которого в два раза больше угла при вершине. Биссектриса угла золотого треугольника подразделяет сторону, с которой она встречается, в золотом сечении, и площади двух разделенных частей также находятся в золотом сечении. [46]
Если угол при вершине золотого гномона трисектор , трисектор снова подразделяет его на меньший золотой гномон и золотой треугольник. Трисектор подразделяет основание в золотом отношении, и две части имеют площади в золотом отношении. Аналогично, любой тупоугольный треугольник может быть подразделен на подобный треугольник и остроугольный равнобедренный треугольник, но золотой гномон является единственным, для которого это подразделение сделано трисектором угла, потому что это единственный равнобедренный треугольник, угол при вершине которого в три раза больше угла при основании. [46]
Мозаики Пенроуза

Золотое сечение занимает видное место в мозаике Пенроуза , семействе апериодических мозаик плоскости, разработанных Роджером Пенроузом , вдохновленных замечанием Иоганна Кеплера о том, что пентаграммы, десятиугольники и другие формы могут заполнять пробелы, которые оставляют только пятиугольные формы при их укладке вместе. [48] Было изучено несколько вариаций этой мозаики, все прототипы которых демонстрируют золотое сечение:
- В оригинальной версии этой мозаики Пенроуза использовались четыре фигуры: правильные пятиугольники и пентаграммы, фигуры «лодок» с тремя вершинами пентаграммы и ромбы в форме «ромба». [49]
- Плитка Пенроуза «воздушный змей и дротик» использует воздушные змеи с тремя внутренними углами в 72° и одним внутренним углом в 144°, а также дротики, вогнутые четырехугольники с двумя внутренними углами в 36°, одним углом в 72° и одним невыпуклым углом в 216°. Специальные правила соответствия ограничивают то, как плитки могут встречаться на любом краю, что приводит к семи комбинациям плиток в любой вершине. Как воздушные змеи, так и дротики имеют стороны двух длин, в золотом сечении друг к другу. Площади этих двух форм плиток также находятся в золотом сечении друг к другу. [48]
- Воздушный змей и дротик можно разрезать по их осям симметрии на пару золотых треугольников и золотых гномонов соответственно. При наличии подходящих правил соответствия эти треугольники, называемые в этом контексте треугольниками Робинсона , можно использовать в качестве прототипов для формы мозаики Пенроуза. [48] [50]
- Ромбическая мозаика Пенроуза содержит два типа ромбов: тонкий ромб с углами 36° и 144° и толстый ромб с углами 72° и 108°. Все длины сторон равны, но отношение длины стороны к короткой диагонали тонкого ромба равно , как и отношение стороны к длинной диагонали толстого ромба. Как и в мозаике воздушного змея и дротика, площади двух ромбов находятся в золотом сечении друг к другу. Опять же, эти ромбы можно разложить на пары треугольников Робинсона. [48]
В треугольниках и четырехугольниках
Строительство Одома
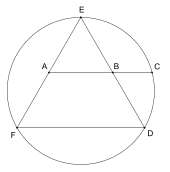
Джордж Одом нашел конструкцию для равностороннего треугольника : если отрезок прямой, соединяющий середины двух сторон, продлен до пересечения с описанной окружностью , то две середины и точка пересечения с окружностью находятся в золотой пропорции. [51]
Треугольник Кеплера
Треугольник Кеплера , названный в честь Иоганна Кеплера , представляет собой уникальный прямоугольный треугольник со сторонами в геометрической прогрессии :
Эти длины сторон являются тремя пифагорейскими средними двух чисел . Три квадрата на его сторонах имеют площади в золотой геометрической прогрессии .
Среди равнобедренных треугольников отношение радиуса вписанной окружности к длине стороны максимально для треугольника, образованного двумя отраженными копиями треугольника Кеплера, разделяющими более длинную из двух своих сторон. [52] Тот же равнобедренный треугольник максимизирует отношение радиуса полукруга на своем основании к его периметру . [53]
Для треугольника Кеплера с наименьшей длиной стороны площадь и острые внутренние углы равны:
Золотой прямоугольник
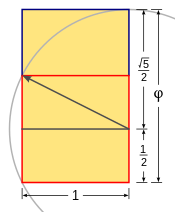
| Нарисуйте квадрат. |
| Проведите линию от середины одной стороны квадрата до противоположного угла. |
| Используя эту линию как радиус, нарисуйте дугу, определяющую высоту прямоугольника. |
| Завершите золотой прямоугольник. |
Золотое сечение соразмеряет длины смежных сторон золотого прямоугольника в пропорции. [54] Наложение золотых прямоугольников дает золотые прямоугольники заново, а удаление или добавление квадратов из золотых прямоугольников оставляет прямоугольники по-прежнему пропорциональными в пропорции. Они могут быть получены золотыми спиралями , через последовательные квадраты и четверти кругов размером с числа Фибоначчи и Лукаса. Они занимают видное место в икосаэдре , а также в додекаэдре (см. раздел ниже для более подробной информации). [55]
Золотой ромб
Золотой ромб — это ромб , диагонали которого пропорциональны золотому сечению, чаще всего . [56] Для ромба таких пропорций его острый угол и тупые углы равны:
Длины его короткой и длинной диагоналей и , выраженные в длинах сторон, равны:
Его площадь, выраженная в единицах ,и :
Его радиус вписанной окружности , выраженный в виде стороны :
Золотые ромбы образуют грани ромбического триаконтаэдра , двух золотых ромбоэдров , додекаэдра Билински [57] и ромбического гексаконтаэдра [56] .
Золотая спираль


Логарифмические спирали — это самоподобные спирали, в которых расстояния, пройденные за один оборот, находятся в геометрической прогрессии . Логарифмическая спираль, радиус которой увеличивается в разы в золотом сечении за каждую четверть оборота, называется золотой спиралью . Эти спирали можно аппроксимировать четвертями окружностей, которые растут в соответствии с золотым сечении [59] , или их аппроксимациями, полученными из чисел Фибоначчи [60] , часто изображаемыми вписанными в спиральный узор из квадратов, растущих в том же соотношении. Точная логарифмическая спиральная форма золотой спирали может быть описана полярным уравнением с :
Не все логарифмические спирали связаны с золотым сечением, и не все спирали, связанные с золотым сечением, имеют ту же форму, что и золотая спираль. Например, другая логарифмическая спираль, охватывающая вложенную последовательность золотых равнобедренных треугольников, растет по золотому сечению на каждые 108°, на которые она поворачивается, вместо угла поворота в 90° золотой спирали. [58] Другая вариация, называемая «лучшей золотой спиралью», растет по золотому сечению на каждые пол-оборота, а не на каждую четверть оборота. [59]
Додекаэдр и икосаэдр

| Декартовы координаты додекаэдра : | ||
| (±1, ±1, ±1) | ||
| (0, ± φ , ± 1/φ ) | ||
| (± 1/φ , 0, ± φ ) | ||
| (± φ , ± 1/φ , 0) | ||
| Вложенный куб внутри додекаэдра изображен пунктирными линиями. | ||
Правильный додекаэдр и его двойственный многогранник икосаэдр являются Платоновыми телами , размеры которых связаны с золотым сечением. Додекаэдр имеет правильные пятиугольные грани, тогда как икосаэдр имеет равносторонние треугольники ; оба имеют ребра . [61]
Для додекаэдра со стороной , радиус описанной и вписанной сферы, а также средний радиус равны ( и соответственно):
В то время как для икосаэдра со стороной , радиус описанной и вписанной сферы, а также средний радиус равны:
Объем и площадь поверхности додекаэдра можно выразить через :
А также для икосаэдра:
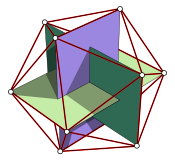
Эти геометрические значения могут быть вычислены из их декартовых координат , которые также могут быть заданы с использованием формул, включающих . Координаты додекаэдра показаны на рисунке выше, тогда как координаты икосаэдра являются циклическими перестановками :
Наборы из трех золотых прямоугольников пересекаются перпендикулярно внутри додекаэдров и икосаэдров, образуя кольца Борромео . [62] [55] В додекаэдрах пары противоположных вершин в золотых прямоугольниках встречаются с центрами пятиугольных граней, а в икосаэдрах они встречаются в его вершинах. В целом, три золотых прямоугольника содержат вершины икосаэдра или, что эквивалентно, пересекают центры граней додекаэдра. [61]
Куб можно вписать в правильный додекаэдр, при этом некоторые диагонали пятиугольных граней додекаэдра служат ребрами куба; следовательно, длины ребер находятся в золотом сечении. Объем куба в раз больше объема додекаэдра. [63] Фактически, золотые прямоугольники внутри додекаэдра находятся в золотых пропорциях к вписанному кубу, так что ребра куба и длинные ребра золотого прямоугольника сами находятся в пропорции. С другой стороны, октаэдр , который является двойственным многогранником куба, может вписать икосаэдр, так что вершины икосаэдра касаются ребер октаэдра в точках, которые делят его ребра в золотом сечении. [64]
Другие свойства
Десятичное расширение золотого сечения можно вычислить с помощью методов поиска корня, таких как метод Ньютона или метод Галлея , на уравнении или на (чтобы вычислить первым). Время, необходимое для вычисления цифр золотого сечения с использованием метода Ньютона, по сути, составляет , где - временная сложность умножения двух -значных чисел. [65] Это значительно быстрее, чем известные алгоритмы для и . Легко запрограммированная альтернатива, использующая только целочисленную арифметику, заключается в вычислении двух больших последовательных чисел Фибоначчи и их делении. Отношение чисел Фибоначчи и каждого из них по цифрам дает по значащим цифрам золотого сечения. Десятичное расширение золотого сечения [1] было вычислено с точностью до десяти триллионов ( ) цифр. [66]
В комплексной плоскости , пятые корни из единицы (для целого числа ) удовлетворяющие являются вершинами пятиугольника. Они не образуют кольцо квадратных целых чисел , однако сумма любого пятого корня из единицы и его комплексно сопряженного числа , является квадратным целым числом, элементом В частности,
Это также справедливо для остальных десятых корней из единицы, удовлетворяющих
Для гамма-функции единственными решениями уравнения являются и .
Когда золотое сечение используется в качестве основания системы счисления (см. основание золотого сечения , иногда называемое финарным или -нарным ), квадратные целые числа в кольце — то есть числа вида for — имеют конечные представления, но рациональные дроби имеют бесконечные представления.
Золотое сечение также появляется в гиперболической геометрии как максимальное расстояние от точки на одной стороне идеального треугольника до ближайшей из двух других сторон: это расстояние, длина стороны равностороннего треугольника, образованного точками касания окружности, вписанной в идеальный треугольник, составляет [67]
Золотое сечение также появляется в теории модулярных функций . Для , пусть
Затем
и
где и в непрерывной дроби следует оценивать как . Функция инвариантна относительно , подгруппы конгруэнции модулярной группы . Также для положительных действительных чисел и тогда [68]
— число Писо–Виджаярагхавана . [69]
Приложения и наблюдения

Архитектура
Швейцарский архитектор Ле Корбюзье , известный своим вкладом в современный международный стиль , сосредоточил свою философию дизайна на системах гармонии и пропорции. Вера Ле Корбюзье в математический порядок вселенной была тесно связана с золотым сечением и рядом Фибоначчи, которые он описывал как «ритмы, очевидные глазу и ясные в их отношениях друг с другом. И эти ритмы лежат в основе человеческой деятельности. Они отзываются в человеке органической неизбежностью, той же прекрасной неизбежностью, которая заставляет детей, стариков, дикарей и ученых вычерчивать Золотое сечение». [70] [71]
Ле Корбюзье явно использовал золотое сечение в своей системе Модулора для масштаба архитектурной пропорции . Он рассматривал эту систему как продолжение давней традиции Витрувия , « Витрувианского человека » Леонардо да Винчи , работ Леона Баттисты Альберти и других, которые использовали пропорции человеческого тела для улучшения внешнего вида и функции архитектуры .
В дополнение к золотому сечению, Ле Корбюзье основал систему на человеческих измерениях , числах Фибоначчи и двойной единице. Он довел предположение о золотом сечении в человеческих пропорциях до крайности: он разделил свою модель человеческого тела по высоте пупка двумя секциями в золотом сечении, затем подразделил эти секции в золотом сечении в коленях и горле; он использовал эти пропорции золотого сечения в системе Модулора . Вилла Ле Корбюзье 1927 года в Гарше стала примером применения системы Модулора. Прямоугольный план виллы, ее высота и внутренняя структура очень близки к золотым прямоугольникам. [72]
Другой швейцарский архитектор, Марио Ботта , основывает многие из своих проектов на геометрических фигурах. Несколько частных домов, которые он спроектировал в Швейцарии, состоят из квадратов и кругов, кубов и цилиндров. В доме, который он спроектировал в Орильо , золотое сечение — это пропорция между центральной секцией и боковыми секциями дома. [73]
Искусство

Иллюстрации Леонардо да Винчи многогранников в Divina Proportione Пачоли заставили некоторых предположить, что он включил золотое сечение в свои картины. Но предположение, что его Мона Лиза , например, использует пропорции золотого сечения, не подтверждается собственными трудами Леонардо. [74] Аналогично, хотя Витрувианский человек Леонардо часто изображается в связи с золотым сечением, пропорции фигуры на самом деле не соответствуют ему, и в тексте упоминаются только целочисленные соотношения. [75] [76]
Сальвадор Дали , находящийся под влиянием работ Матилы Гики , [77] явно использовал золотое сечение в своем шедевре «Таинство Тайной Вечери» . Размеры холста представляют собой золотой прямоугольник. Огромный додекаэдр, в перспективе так, что ребра кажутся в золотом отношении друг к другу, подвешен над Иисусом и позади него и доминирует в композиции. [74] [78]
Статистическое исследование 565 произведений искусства разных великих художников, проведенное в 1999 году, показало, что эти художники не использовали золотое сечение в размере своих холстов. Исследование пришло к выводу, что среднее соотношение двух сторон изученных картин соответствует средним значениям для отдельных художников, начиная от (Гойи) до (Беллини). [79] С другой стороны, Пабло Тосто перечислил более 350 работ известных художников, включая более 100, которые имеют холсты с золотым прямоугольником и пропорциями, а также другие с пропорциями, такими как и [80]

Книги и дизайн
По словам Яна Чихольда ,
Было время, когда отклонения от действительно красивых пропорций страницы и Золотого сечения были редки. Многие книги, выпущенные между 1550 и 1770 годами, показывают эти пропорции точно, с точностью до половины миллиметра. [82]
Согласно некоторым источникам, золотое сечение используется в повседневном дизайне, например, в пропорциях игральных карт, открыток, плакатов, выключателей и широкоэкранных телевизоров. [83]
Флаги

По словам дизайнера, соотношение сторон (ширина-высота) флага Того должно было соответствовать золотому сечению. [84]
Музыка
Эрнё Лендваи анализирует работы Белы Бартока как основанные на двух противоположных системах: золотом сечении и акустической шкале , [85] хотя другие исследователи музыки отвергают этот анализ. [86] Французский композитор Эрик Сати использовал золотое сечение в нескольких своих произведениях, включая Sonneries de la Rose+Croix . Золотое сечение также очевидно в организации разделов в музыке Reflets dans l'eau (Отражения в воде) Дебюсси из Images (1-я серия, 1905), в которой «последовательность тональностей обозначена интервалами 34, 21, 13 и 8, а главная кульминация находится в позиции фи». [87]
Музыковед Рой Ховат заметил, что формальные границы La Mer Дебюсси точно соответствуют золотому сечению. [88] Трезис находит внутренние доказательства «замечательными», но предупреждает, что никакие письменные или зарегистрированные свидетельства не указывают на то, что Дебюсси сознательно стремился к таким пропорциям. [89]
Теоретики музыки, включая Ганса Цендера и Хайнца Болена, экспериментировали со шкалой 833 цента , музыкальной шкалой, основанной на использовании золотого сечения в качестве ее фундаментального музыкального интервала . При измерении в центах , логарифмической шкале для музыкальных интервалов, золотое сечение составляет приблизительно 833,09 цента. [90]
Природа

Иоганн Кеплер писал, что «образ мужчины и женщины проистекает из божественной пропорции. По моему мнению, размножение растений и деторождение животных находятся в том же соотношении» [91] .
Психолог Адольф Цейзинг отметил, что золотое сечение проявляется в филлотаксисе , и на основании этих закономерностей в природе утверждал , что золотое сечение является универсальным законом. [92] В 1854 году Цейзинг написал об универсальном ортогенетическом законе «стремления к красоте и полноте в сферах как природы, так и искусства». [93]
Однако некоторые утверждают, что многие очевидные проявления золотого сечения в природе, особенно в отношении размеров животных, являются вымышленными. [94]
Физика
Квазиодномерный ферромагнетик Изинга (ниобат кобальта) имеет 8 предсказанных состояний возбуждения (с симметрией E 8 ), которые при исследовании с помощью нейтронного рассеяния показали, что два самых низких состояния находятся в золотом сечении. В частности, эти квантовые фазовые переходы во время возбуждения спина, которые происходят при температуре, близкой к абсолютному нулю, показали пары перегибов в его упорядоченной фазе к переворотам спина в его парамагнитной фазе; обнаружив, чуть ниже его критического поля , спиновую динамику с острыми модами при низких энергиях, приближающихся к золотому сечению. [95]
Оптимизация
Не существует известного общего алгоритма для равномерного расположения заданного числа узлов на сфере для любого из нескольких определений равномерного распределения (см., например, задачу Томсона или задачу Таммеса ). Однако полезное приближение получается путем деления сферы на параллельные полосы равной площади поверхности и размещения одного узла в каждой полосе на долготах, отстоящих друг от друга на золотое сечение круга, т. е. Этот метод использовался для размещения 1500 зеркал спутника Starshine-3 , в котором принимали участие студенты . [96]
Золотое сечение также является важнейшим элементом поиска золотого сечения .
Спорные наблюдения
Примеры спорных наблюдений золотого сечения включают в себя следующее:

- Конкретные пропорции в телах позвоночных (включая людей) часто утверждают, что они находятся в золотом сечении; например, соотношение последовательных фаланговых и пястных костей (костей пальцев) считается приближенным к золотому сечению. Однако существуют большие различия в реальных размерах этих элементов у конкретных людей, и рассматриваемая пропорция часто значительно отличается от золотого сечения. [97] [98]
- Раковины моллюсков, таких как наутилус, часто считаются имеющими золотую пропорцию. [99] Рост раковин наутилуса следует логарифмической спирали , и иногда ошибочно утверждается, что любая логарифмическая спираль связана с золотой пропорцией, [100] или иногда утверждается, что каждая новая камера имеет золотую пропорцию относительно предыдущей. [101] Однако измерения раковин наутилуса не подтверждают это утверждение. [102]
- Историк Джон Мэн утверждает, что и страницы, и текстовая область Библии Гутенберга были «основаны на форме золотого сечения». Однако, согласно его собственным измерениям, соотношение высоты к ширине страниц составляет [103]
- Исследования психологов, начиная с Густава Фехнера около 1876 года , [104] были разработаны для проверки идеи о том, что золотое сечение играет роль в восприятии красоты человеком . В то время как Фехнер обнаружил предпочтение прямоугольным соотношениям, основанным на золотом сечении, более поздние попытки тщательно проверить такую гипотезу были, в лучшем случае, безрезультатными. [105] [74]
- В инвестировании некоторые специалисты по техническому анализу используют золотое сечение для указания поддержки уровня цен или сопротивления росту цен акций или товаров; после значительных изменений цен вверх или вниз, новые уровни поддержки и сопротивления предположительно находятся на уровне или около цен, связанных с начальной ценой через золотое сечение. [106] Использование золотого сечения в инвестировании также связано с более сложными моделями, описываемыми числами Фибоначчи (например, волновой принцип Эллиотта и коррекция Фибоначчи ). Однако другие аналитики рынка опубликовали анализы, предполагающие, что эти проценты и модели не подтверждаются данными. [107]
египетские пирамиды

Пирамида Хеопса или Хуфу была проанализирована пирамидологами как имеющая двойной треугольник Кеплера в качестве своего поперечного сечения. Если бы эта теория была верна, золотое сечение описывало бы отношение расстояний от середины одной из сторон пирамиды до ее вершины и от той же середины до центра основания пирамиды. Однако неточность измерений, вызванная отчасти удалением внешней поверхности пирамиды, делает невозможным отличить эту теорию от других числовых теорий пропорций пирамиды, основанных на числе Пи или на отношениях целых чисел. Современные ученые сходятся во мнении, что пропорции этой пирамиды не основаны на золотом сечении, потому что такая основа не соответствовала бы как тому, что известно о египетской математике со времени строительства пирамиды, так и египетским теориям архитектуры и пропорций, использованным в их других работах. [108]
Парфенон

Фасад Парфенона (ок. 432 г. до н. э . ), а также элементы его фасада и другие части, как утверждают некоторые, были ограничены золотыми прямоугольниками. [110] Другие ученые отрицают, что у греков была какая-либо эстетическая связь с золотым сечением. Например, Кейт Девлин говорит: «Безусловно, часто повторяемое утверждение о том, что Парфенон в Афинах основан на золотом сечении, не подтверждается фактическими измерениями. Фактически, вся история о греках и золотом сечении, кажется, не имеет под собой никаких оснований». [111] Мидхат Дж. Газале утверждает, что «только при Евклиде... были изучены математические свойства золотого сечения». [112]
Измерив 15 храмов, 18 монументальных гробниц, 8 саркофагов и 58 надгробных стел с пятого века до нашей эры по второй век нашей эры, один исследователь пришел к выводу, что золотое сечение полностью отсутствовало в греческой классической архитектуре пятого века до нашей эры и почти отсутствовало в течение следующих шести столетий. [113] Более поздние источники, такие как Витрувий (первый век до нашей эры), обсуждают исключительно пропорции, которые могут быть выражены целыми числами, то есть соразмерные, в отличие от иррациональных пропорций.
Современное искусство

Section d'Or («Золотое сечение») было коллективом художников , скульпторов, поэтов и критиков, связанных с кубизмом и орфизмом . [114] Действуя с 1911 по 1914 год, они приняли это название как для того, чтобы подчеркнуть, что кубизм представляет собой продолжение великой традиции, а не является изолированным движением, так и в знак уважения к математической гармонии, связанной с Жоржем Сёра . [115] (Некоторые авторы утверждали, что Сёра использовал золотое сечение в своих картинах, но сочинения и картины Сёра предполагают, что он использовал простые целочисленные соотношения, и любое приближение к золотому сечению было случайным.) [116] Кубисты наблюдали в своих гармониях геометрическую структуризацию движения и формы, «примат идеи над природой», «абсолютную научную ясность концепции». [117] Однако, несмотря на этот общий интерес к математической гармонии, было ли использовано золотое сечение в композициях картин, представленных на знаменитой выставке Salon de la Section d'Or 1912 года, определить сложнее. Ливио, например, утверждает, что они этого не делали, [118] и Марсель Дюшан сказал об этом в интервью. [119] С другой стороны, анализ показывает, что Хуан Грис использовал золотое сечение при составлении произведений, которые, вероятно, но не окончательно, были показаны на выставке. [119] [120] Историк искусства Дэниел Роббинс утверждает, что в дополнение к отсылке к математическому термину название выставки также относится к более ранней группе Bandeaux d'Or , в которую были вовлечены Альбер Глез и другие бывшие члены Abbaye de Créteil . [121]
Говорят, что Пит Мондриан широко использовал золотое сечение в своих геометрических картинах, [122] хотя другие эксперты (включая критика Ива-Алена Буа ) опровергли эти утверждения. [74] [123]
Смотрите также
- Список работ, выполненных с использованием золотого сечения
- Металлический средний
- Коэффициент пластичности
- Сакральная геометрия
- Суперзолотое сечение
- Коэффициент серебра
Ссылки
Пояснительные сноски
- ^ Если снять ограничение на и , каждое из которых больше нуля, то на самом деле существует два решения этого уравнения: одно положительное и одно отрицательное. определяется как положительное решение. Отрицательное решение — Сумма двух решений — , а произведение двух решений — .
- ^ Другие названия включают золотую середину , золотое сечение , [4] золотое сечение , [5] золотую пропорцию , золотое число , [6] срединное сечение и божественное сечение .
- ↑ Евклид, Элементы , Книга II, Предложение 11; Книга IV, Предложение 10–11; Книга VI, Предложение 30; Книга XIII, Предложение 1–6, 8–11, 16–18.
- Ссылки μεῖζον τμῆμα, οὕτως τὸ μεῖζον πρὸς τὸ ἔλαττὸν». [18]
- ↑ В честь классического греческого скульптора Фидия (ок. 490–430 гг. до н. э.); [33] Барр позже писал, что он считал маловероятным, что Фидий на самом деле использовал золотое сечение. [34]
Цитаты
- ^ abc Sloane, N. J. A. (ред.). "Последовательность A001622 (Десятичное разложение золотого сечения phi (или tau) = (1 + sqrt(5))/2)". Онлайновая энциклопедия целочисленных последовательностей . Фонд OEIS.
- ^ Евклид. «Книга 6, Определение 3». Элементы .
- ^ Пачоли, Лука (1509). Божественная пропорция . Венеция: Лука Паганинем де Паганинус де Брешиа (Антонио Капелла).
- ↑ Ливио 2002, стр. 3, 81.
- ^ Саммерсон, Джон (1963). Небесные особняки и другие эссе об архитектуре. Нью-Йорк: WW Norton. стр. 37.
И то же самое применимо в архитектуре к
прямоугольникам
, представляющим эти и другие соотношения (например, «золотое сечение»). Единственная ценность этих соотношений в том, что они интеллектуально плодотворны и предполагают ритмы модульного дизайна.
- ^ Герц-Фишлер 1998.
- ^ Герц-Фишлер 1998, стр. 20–25.
- ^ Строгац, Стивен (24.09.2012). «Я, снова я и математика: контроль пропорций». The New York Times .
- ^ Шилак, Винсент П. (1987). «Последовательность Фибоначчи и золотое сечение». Учитель математики . 80 (5): 357–358. doi :10.5951/MT.80.5.0357. JSTOR 27965402.В этом источнике содержится элементарный вывод значения золотого сечения.
- ^ Питерс, Дж. М. Х. (1978). «Приблизительное соотношение между π и золотым сечением». The Mathematical Gazette . 62 (421): 197–198. doi :10.2307/3616690. JSTOR 3616690. S2CID 125919525.
- ^ Ливио 2002, стр. 6.
- ↑ Ливио 2002, стр. 4: «... линейное деление, которое Евклид определил для... чисто геометрических целей...»
- ↑ Ливио 2002, стр. 7–8.
- ↑ Ливио 2002, стр. 4–5.
- ^ Ливио 2002, стр. 78.
- ^ Хеменуэй, Прия (2005). Божественная пропорция: Phi в искусстве, природе и науке . Нью-Йорк: Sterling. С. 20–21. ISBN 9781402735226.
- ^ Ливио 2002, стр. 3.
- ^ Евклид (2007). Элементы геометрии Евклида . Перевод Фицпатрика, Ричарда. Lulu.com. стр. 156. ISBN 978-0615179841.
- ↑ Ливио 2002, стр. 88–96.
- ^ Маккиннон, Ник (1993). «Портрет Фра Луки Пачоли». The Mathematical Gazette . 77 (479): 130–219. doi :10.2307/3619717. JSTOR 3619717. S2CID 195006163.
- ↑ Ливио 2002, стр. 131–132.
- ^ Baravalle, HV (1948). «Геометрия пятиугольника и золотое сечение». Учитель математики . 41 : 22–31. doi :10.5951/MT.41.1.0022.
- ↑ Ливио 2002, стр. 134–135.
- ^ Ливио 2002, стр. 141.
- ^ Шрайбер, Питер (1995). «Дополнение к статье Дж. Шаллита «Истоки анализа алгоритма Евклида». Historia Mathematica . 22 (4): 422–424. doi : 10.1006/hmat.1995.1033 .
- ↑ Ливио 2002, стр. 151–152.
- ^ О'Коннор, Джон Дж.; Робертсон, Эдмунд Ф. (2001). "Золотое сечение". Архив истории математики MacTutor . Получено 18 сентября 2007 г.
- ^ Финк, Карл (1903). Краткая история математики. Перевод Бемана, Вустера Вудраффа; Смита, Дэвида Юджина (2-е изд.). Чикаго: Open Court. стр. 223.(Первоначально опубликовано как Geschichte der Elementar-Mathematik .)
- ^ Бойтельспехер, Альбрехт; Петри, Бернхард (1996). «Фибоначчи-Зален». Золотой Шнитт . Einblick in die Wissenschaft (на немецком языке). Vieweg+Teubner Verlag. стр. 87–98. дои : 10.1007/978-3-322-85165-9_6. ISBN 978-3-8154-2511-4.
- ^ Герц-Фишлер 1998, стр. 167–170.
- ^ Посаментье и Леманн 2011, с. 8.
- ^ Посаментье и Леманн 2011, с. 285.
- ↑ Кук, Теодор Андреа (1914). Кривые жизни. Лондон: Констебль. С. 420.
- ^ Барр, Марк (1929). «Параметры красоты». Архитектура (Нью-Йорк) . Т. 60. С. 325.Перепечатано: «Параметры красоты». Think . Т. 10–11. IBM . 1944.
- ^ Ливио 2002, стр. 5.
- ^ Гарднер, Мартин (2001). "7. Плитки Пенроуза". Колоссальная книга математики . Нортон. стр. 73–93.
- ^
Livio 2002, стр. 203–209 Gratias, Denis ; Quiquandon, Marianne (2019). «Открытие квазикристаллов: первые дни». Comptes Rendus Physique . 20 (7–8): 803–816. Bibcode :2019CRPhy..20..803G. doi : 10.1016/j.crhy.2019.05.009 . S2CID 182005594.
Ярич, Марко В. (1989). Введение в математику квазикристаллов . Academic Press. стр. x. ISBN 9780120406029.Хотя к моменту открытия квазикристаллов теория квазипериодических функций была известна уже почти шестьдесят лет, именно математика апериодических мозаик Пенроуза, в основном разработанная Николаасом де Брейном , оказала основное влияние на новую область.
Goldman, Alan I.; Anderegg, James W.; Besser, Matthew F.; Chang, Sheng-Liang; Delaney, Drew W.; Jenks, Cynthia J .; Kramer, Matthew J.; Lograsso, Thomas A.; Lynch, David W.; McCallum, R. William; Shield, Jeffrey E.; Sordelet, Daniel J.; Thiel, Patricia A. (1996). «Квазикристаллические материалы». American Scientist . 84 (3): 230–241. JSTOR 29775669. - ^ Мартин, Джордж Э. (1998). Геометрические построения . Бакалаврские тексты по математике. Springer. стр. 13–14. doi :10.1007/978-1-4612-0629-3. ISBN 978-1-4612-6845-1.
- ^ Хейлперин, Макс; Кайзер, Барбара К.; Найт, Карл В. (1999). Конкретные абстракции: Введение в информатику с использованием схемы. Brooks/Cole. стр. 63.
- ^ Харди, GH ; Райт, EM (1960) [1938]. "§11.8. Мера наиболее близких приближений к произвольному иррациональному" . Введение в теорию чисел (4-е изд.). Oxford University Press. стр. 163–164. ISBN 978-0-19-853310-8.
- ^ Sizer, Walter S. (1986). «Продолженные корни». Mathematics Magazine . 59 (1): 23–27. doi :10.1080/0025570X.1986.11977215. JSTOR 2690013. MR 0828417.
- ^ Таттерсолл, Джеймс Джозеф (1999). Элементарная теория чисел в девяти главах . Cambridge University Press. стр. 28.
- ^ Паркер, Мэтт (2014). Что делать и делать в четвертом измерении . Фаррар, Штраус и Жиру. стр. 284. ISBN 9780374275655.
- ^ Кинг, С.; Бек, Ф.; Люттге, У. (2004). «О тайне золотого угла в филлотаксисе». Растение, клетка и окружающая среда . 27 (6): 685–695. doi :10.1111/j.1365-3040.2004.01185.x.
- ^ Флетчер, Рэйчел (2006). «Золотое сечение». Nexus Network Journal . 8 (1): 67–89. doi : 10.1007/s00004-006-0004-z . S2CID 120991151.
- ^ abcde Лёб, Артур (1992). «Золотой треугольник». Концепции и изображения: Визуальная математика . Биркхойзер. стр. 179–192. doi :10.1007/978-1-4612-0343-8_20. ISBN 978-1-4612-6716-4.
- ^ Миллер, Уильям (1996). «Пентагоны и золотые треугольники». Математика в школе . 25 (4): 2–4. JSTOR 30216571.
- ^ abcd Грюнбаум, Бранко ; Шепард, GC (1987). Tilings and Patterns. Нью-Йорк: WH Freeman. С. 537–547. ISBN 9780716711933.
- ^ Пенроуз, Роджер (1978). «Пентаплексность». Эврика . Т. 39. С. 32.(оригинальный PDF)
- ^ Фреттлех, Д.; Харрис, Э.; Гелер, Ф. «Треугольник Робинсона». Энциклопедия мозаики .
Клейсон, Роберт Г. (1994). «Семейство узоров из золотых треугольных плиток». The Mathematical Gazette . 78 (482): 130–148. doi :10.2307/3618569. JSTOR 3618569. S2CID 126206189.
- ^ Одом, Джордж; ван де Краатс, Ян (1986). "E3007: Золотое сечение из равностороннего треугольника и его описанной окружности". Задачи и решения. The American Mathematical Monthly . 93 (7): 572. doi :10.2307/2323047. JSTOR 2323047.
- ^ Басард, Хьюберт LL (1968). «L'algèbre au Moyen Âge: le «Liber mensurationum» d'Abû Bekr». Journal des Savants (на французском и латыни). 1968 (2): 65–124. дои : 10.3406/jds.1968.1175.См. задачу 51, воспроизведенную на стр. 98.
- ^ Брюс, Ян (1994). «Еще один пример золотого прямоугольного треугольника» (PDF) . Fibonacci Quarterly . 32 (3): 232–233. doi :10.1080/00150517.1994.12429219.
- ^ Посаментье и Леманн 2011, с. 11.
- ^ ab Burger, Edward B.; Starbird, Michael P. (2005) [2000]. Сердце математики: Приглашение к эффективному мышлению (2-е изд.). Springer. стр. 382. ISBN 9781931914413.
- ^ ab Grünbaum, Branko (1996). "Новый ромбический гексеконтаэдр" (PDF) . Геомбинаторика . 6 (1): 15–18.
- ^ Сенешаль, Марджори (2006). «Дональд и золотые ромбоэдры». В Дэвисе, Чандлере; Эллерсе, Эрихе В. (ред.). Наследие Коксетера . Американское математическое общество. стр. 159–177. ISBN 0-8218-3722-2.
- ^ ab Loeb, Arthur L.; Varney, William (март 1992). «Существует ли золотая спираль, и если нет, то где ее центр?». В Hargittai, István; Pickover, Clifford A. (ред.). Спиральная симметрия . World Scientific. стр. 47–61. doi :10.1142/9789814343084_0002. ISBN 978-981-02-0615-4.
- ^ ab Reitebuch, Ulrich; Skrodzki, Martin; Polthier, Konrad (2021). «Аппроксимация логарифмических спиралей четвертями окружностей». В Swart, David; Farris, Frank; Torrence, Eve (ред.). Proceedings of Bridges 2021: Mathematics, Art, Music, Architecture, Culture . Phoenix, Arizona: Tessellations Publishing. стр. 95–102. ISBN 978-1-938664-39-7.
- ^ Дидрихс, Данило Р. (февраль 2019 г.). «Архимедовы, логарифмические и эйлеровы спирали – интригующие и вездесущие закономерности в природе». The Mathematical Gazette . 103 (556): 52–64. doi :10.1017/mag.2019.7. S2CID 127189159.
- ^ аб Ливио (2002, стр. 70–72)
- ^ Ганн, Чарльз; Салливан, Джон М. (2008). «Кольца Борромео: Видео о новом логотипе ИДУ». В Сарханги, Реза; Секин, Карло Х. (ред.). Труды Бриджеса 2008 . Леуварден, Нидерланды. Публикации Тарквина. стр. 63–70.; Видео на "The Borromean Rings: A new logo for the IMU". Международный математический союз . Архивировано из оригинала 2021-03-08.
- ^ Хьюм, Альфред (1900). «Некоторые предложения о правильном додекаэдре». The American Mathematical Monthly . 7 (12): 293–295. doi :10.2307/2969130. JSTOR 2969130.
- ^ Coxeter, HSM ; du Val, Patrick ; Flather, HT; Petrie, JF (1938). The Fifty-Nine Icosahedra . Vol. 6. University of Toronto Studies. p. 4.
Так же, как тетраэдр может быть вписан в куб, так и куб может быть вписан в додекаэдр. Взаимно-поступательным движением это приводит к октаэдру, описанному около икосаэдра. Фактически, каждая из двенадцати вершин икосаэдра делит ребро октаэдра в соответствии с «золотым сечением».
- ^ Muller, JM (2006). Элементарные функции: алгоритмы и реализация (2-е изд.). Бостон: Birkhäuser. стр. 93. ISBN 978-0817643720.
- ^ Йи, Александр Дж. (13.03.2021). «Рекорды, установленные y-cruncher». numberword.org .Два независимых вычисления, выполненные Клиффордом Спилманом.
- ^ Horocycles exinscrits: une proprieté Hyperbolique Remarquable, cabri.net, получено 21 июля 2009 г.
- ^ Берндт, Брюс С.; Чан, Хэн Хуат; Хуан, Сен-Шань; Кан, Сун-И; Сон, Джебум; Сон, Сын Хван (1999). "The Rogers–Ramanujan Continued Fraction" (PDF) . Журнал вычислительной и прикладной математики . 105 (1–2): 9–24. doi :10.1016/S0377-0427(99)00033-3. Архивировано из оригинала (PDF) 2022-10-06 . Получено 2022-11-29 .
- ^ Даффин, Ричард Дж. (1978). «Алгоритмы локализации корней многочлена и чисел Пизо Виджаярагхавана». Pacific Journal of Mathematics . 74 (1): 47–56. doi : 10.2140/pjm.1978.74.47 .
- ^ Ле Корбюзье, Модулор , стр. 25 , как цитируется в Padovan, Richard (1999). Пропорция: Наука, Философия, Архитектура . Тейлор и Фрэнсис. стр. 316. doi :10.4324/9780203477465. ISBN 9781135811112.
- ^ Фрингс, Маркус (2002). «Золотое сечение в архитектурной теории». Nexus Network Journal . 4 (1): 9–32. doi : 10.1007/s00004-001-0002-0 . S2CID 123500957.
- ^ Ле Корбюзье, Модулор , стр. 35 , как цитируется в Padovan, Richard (1999). Пропорция: Наука, Философия, Архитектура . Тейлор и Фрэнсис. стр. 320. doi :10.4324/9780203477465. ISBN 9781135811112.
И в картинах, и в архитектурных проектах используется золотое сечение.
- ^ Урвин, Саймон (2003). Анализ архитектуры (2-е изд.). Routledge. С. 154–155.
- ^ abcd Livio, Mario (2002). «Золотое сечение и эстетика». Plus Magazine . Получено 26 ноября 2018 г.
- ^ Devlin, Keith (2007). "The Myth That Will Not Go Away". Архивировано из оригинала 12 ноября 2020 г. . Получено 26 сентября 2013 г.
Частью процесса становления писателя-математика, по-видимому, является изучение того, что вы не можете ссылаться на золотое сечение, не сопровождая первое упоминание фразой, которая звучит примерно так: "которое древние греки и другие считали имеющим божественные и мистические свойства". Почти столь же навязчивым является желание добавить второй фактоид вроде "Леонардо да Винчи считал, что человеческая форма отображает золотое сечение". Нет ни малейшего доказательства, подтверждающего любое из утверждений, и есть все основания предполагать, что оба они ложны. Тем не менее, оба утверждения, наряду с различными другими в похожем ключе, продолжают жить.
- ^ Simanek, Donald E. "Fibonacci Flim-Flam". Архивировано из оригинала 9 января 2010 г. Получено 9 апреля 2013 г.
- ^ Сальвадор Дали (2008). Измерение Дали: Расшифровка сознания гения (DVD) . Медиа 3.14-TVC-FGSD-IRL-AVRO.
- ^ Хант, Карла Херндон; Джилки, Сьюзен Никодемус (1998). Преподавание математики в блоке . Взгляд на образование. стр. 44, 47. ISBN 1-883001-51-X.
- ^ Олариу, Агата (1999). «Золотое сечение и искусство живописи». arXiv : physics/9908036 .
- ^ Тосто, Пабло (1969). La composición áurea en las artes plásticas [ Золотая композиция в пластическом искусстве ] (на испанском языке). Хашетт. стр. 134–144.
- ^ Чихольд, Ян (1991). Форма книги. Hartley & Marks. стр. 43 Рис. 4. ISBN 0-88179-116-4.
Структура идеальных пропорций в средневековой рукописи без нескольких колонок. Определена Яном Чихольдом в 1953 году. Пропорции страницы 2:3. Пропорции полей 1:1:2:3, Текстовая область пропорциональна Золотому сечению. Нижний внешний угол текстовой области также зафиксирован диагональю.
- ^ Чихольд, Ян (1991). Форма книги. Hartley & Marks. стр. 27–28. ISBN 0-88179-116-4.
- ^ Джонс, Рональд (1971). «Золотое сечение: самая замечательная мера». The Structurist . 11 : 44–52.
Кто бы мог заподозрить, например, что пластина переключателя для выключателей с одной лампой стандартизирована в терминах золотого прямоугольника?
Джонсон, Арт (1999). Знаменитые проблемы и их математики . Teacher Ideas Press. стр. 45. ISBN 9781563084461Золотое сечение
является стандартной чертой многих современных дизайнов: от открыток и кредитных карт до плакатов и выключателей.
Стахов, Алексей П .; Олсен, Скотт (2009). "§1.4.1 Золотой прямоугольник с отношением сторон τ". Математика гармонии: от Евклида до современной математики и компьютерных наук . World Scientific. стр. 20–21.
Кредитная карта имеет форму золотого прямоугольника
Кокс, Саймон (2004). Взлом кода да Винчи. Barnes & Noble. стр. 62. ISBN 978-1-84317-103-4.
Золотое сечение также появляется в некоторых совсем неожиданных местах: широкоэкранные телевизоры, открытки, кредитные карты и фотографии — все они обычно соответствуют его пропорциям.
- ↑ Posamentier & Lehmann 2011, глава 4, сноска 12: «Флаг Того был разработан художником Полем Ахи (1930–2010), который утверждает, что пытался построить флаг в форме золотого прямоугольника».
- ^ Лендваи, Эрно (1971). Бела Барток: анализ его музыки . Лондон: Кан и Аверилл.
- ^ Ливио 2002, стр. 190.
- ^ Смит, Питер Ф. (2003). Динамика восторга: архитектура и эстетика. Routledge. стр. 83. ISBN 9780415300100.
- ^ Ховат, Рой (1983). «1. Пропорциональная структура и золотое сечение». Дебюсси в пропорции: музыкальный анализ . Cambridge University Press. стр. 1–10.
- ^ Трезис, Саймон (1994). Дебюсси: La Mer. Cambridge University Press. стр. 53. ISBN 9780521446563.
- ^ Монговен, Кейси (2010). «Стиль музыки, характеризующийся Фибоначчи и золотым сечением» (PDF) . Congressus Numerantium . 201 : 127–138.
Хасегава, Роберт (2011). « Гармония в музыке Ганса Цендера». Перспективы новой музыки . 49 (1). Проект Muse: 207–234. doi :10.1353/pnm.2011.0000. JSTOR 10.7757/persnewmusi.49.1.0207.
Сметерст, Рейлли (2016). «Две неоктавные настройки Хайнца Болена: практическое предложение». В Торренсе, Ив; и др. (ред.). Труды Bridges 2016. Ювяскюля, Финляндия. Tessellations Publishing. стр. 519–522.
- ^ Ливио 2002, стр. 154.
- ^ Падован, Ричард (1999). Пропорция: Наука, Философия, Архитектура . Тейлор и Фрэнсис. стр. 305–306. doi :10.4324/9780203477465. ISBN 9781135811112.
Падован, Ричард (2002). «Пропорция: наука, философия, архитектура». Nexus Network Journal . 4 (1): 113–122. doi : 10.1007/s00004-001-0008-7 .
- ^ Цейзинг, Адольф (1854). «Einleitung [предисловие]». Neue Lehre von den Proportionen des menschlichen Körpers [ Новая доктрина пропорций человеческого тела ] (на немецком языке). Вейгель. стр. 1–10.
- ^ Поммерсхайм, Джеймс Э.; Маркс, Тим К.; Флапан, Эрика Л. , ред. (2010). Теория чисел: живое введение с доказательствами, приложениями и историями . Wiley. стр. 82.
- ^ Coldea, R.; Tennant, DA; Wheeler, EM; Wawrzynksa, E.; Prabhakaran, D.; Telling, M.; Habicht, K.; Smeibidl, P.; Keifer, K. (2010). «Квантовая критичность в цепочке Изинга: экспериментальное доказательство возникающей симметрии E8». Science . 327 (5962): 177–180. arXiv : 1103.3694 . Bibcode :2010Sci...327..177C. doi :10.1126/science.1180085. PMID 20056884. S2CID 206522808.
- ^ "Диско-шар в космосе". NASA. 2001-10-09. Архивировано из оригинала 2020-12-22 . Получено 2007-04-16 .
- ^ Фазант, Стивен (1986). Bodyspace . Тейлор и Фрэнсис. ISBN 9780850663402.
- ^ ван Лаак, Уолтер (2001). Лучшая история нашего мира: Том 1 Вселенная . Ахен: ван Лаах.
- ^ Данлэп, Ричард А. (1997). Золотое сечение и числа Фибоначчи . World Scientific. стр. 130.
- ^ Фальбо, Клемент (март 2005 г.). «Золотое сечение — противоположная точка зрения». The College Mathematics Journal . 36 (2): 123–134. doi :10.1080/07468342.2005.11922119. S2CID 14816926.
- ^ Москович, Иван (2004). Шарнирный квадрат и другие головоломки. Нью-Йорк: Sterling. стр. 122. ISBN 9781402716669.
- ^ Петерсон, Иварс (1 апреля 2005 г.). «Спирали морских ракушек». Science News . Архивировано из оригинала 3 октября 2012 г. Получено 10 ноября 2008 г.
- ^ Man, John (2002). Гутенберг: Как один человек переделал мир с помощью слова. Wiley. С. 166–167. ISBN 9780471218234.
Страница размером в пол-фолио (30,7 × 44,5 см) состояла из двух прямоугольников — всей страницы и ее текстовой области — на основе так называемого «золотого сечения», которое определяет важнейшее соотношение между короткими и длинными сторонами и дает иррациональное число, как и число Пи, но представляет собой соотношение примерно 5:8.
- ^ Фехнер, Густав (1876). Vorschule der Ästhetik [ Дошкольная школа эстетики ] (на немецком языке). Лейпциг: Breitkopf & Härtel. стр. 190–202.
- ↑ Ливио 2002, стр. 7.
- ^ Ослер, Кэрол (2000). «Поддержка сопротивления: технический анализ и внутридневные обменные курсы» (PDF) . Обзор экономической политики Федерального резервного банка Нью-Йорка . 6 (2): 53–68. Архивировано (PDF) из оригинала 2007-05-12.
38,2 процента и 61,8 процента откатов недавних подъемов или спадов являются обычным явлением,
- ^ Батчелор, Рой ; Рамьяр, Ричард (2005). Магические числа в индексе Доу-Джонса (отчет). Cass Business School. стр. 13, 31.Популярные обзоры прессы можно найти в: Стивенсон, Том (2006-04-10). «С тех пор, как в эпоху «большое прекрасно», гиганты не выглядели лучше». The Daily Telegraph .«Технический сбой». The Economist . 2006-09-23.
- ^ Герц-Фишлер, Роджер (2000). Форма Великой пирамиды . Wilfrid Laurier University Press. ISBN 0-88920-324-5.Вся книга рассматривает множество альтернативных теорий относительно формы этой пирамиды. См. Главу 11, «Теория треугольника Кеплера», стр. 80–91, для материала, специфичного для треугольника Кеплера, и стр. 166 для заключения о том, что теория треугольника Кеплера может быть устранена принципом, что «Теория должна соответствовать уровню математики, согласующемуся с тем, что было известно древним египтянам». См. примечание 3, стр. 229, для истории работы Кеплера с этим треугольником.
Росси, Коринна (2004). Архитектура и математика в Древнем Египте. Издательство Кембриджского университета. стр. 67–68.
нет прямых доказательств ни в одном древнеегипетском письменном математическом источнике каких-либо арифметических вычислений или геометрических построений, которые можно было бы классифицировать как Золотое сечение... сходимость к , и само по себе как число, не соответствуют существующим математическим источникам Среднего царства
; см. также обширное обсуждение нескольких альтернативных теорий формы пирамиды и другой египетской архитектуры, стр. 7–56Росси, Коринна; Тут, Кристофер А. (2002). «Были ли известны ряд Фибоначчи и золотое сечение в Древнем Египте?». Historia Mathematica . 29 (2): 101–113. doi :10.1006/hmat.2001.2334. hdl : 11311/997099 .
Марковски, Джордж (1992). "Заблуждения о золотом сечении" (PDF) . The College Mathematics Journal . 23 (1). Математическая ассоциация Америки: 2–19. doi :10.2307/2686193. JSTOR 2686193 . Получено 29.06.2012 .
Похоже, египтяне даже не знали о существовании, а тем более включали его в свои здания
- ↑ Ливио 2002, стр. 74–75.
- ^ Ван Мерсберген, Одри М. (1998). «Риторические прототипы в архитектуре: измерение Акрополя с помощью философской полемики». Communication Quarterly . 46 (2): 194–213. doi :10.1080/01463379809370095.
- ^ Девлин, Кит Дж. (2005). Математический инстинкт. Нью-Йорк: Thunder's Mouth Press. С. 108.
- ^ Газале, Мидхат Дж . (1999). Гномон: от фараонов к фракталам . Принстон. п. 125. ИСБН 9780691005140.
- ^ Футакис, Патрис (2014). «Строили ли греки согласно золотому сечению?». Cambridge Archaeological Journal . 24 (1): 71–86. doi :10.1017/S0959774314000201. S2CID 162767334.
- ^ Салон де ла Секция д'Ор, октябрь 1912 г., Центр посредничества Помпиду
- ^ Jeunes Peintres ne vous frappez pas !, Lasection d'Or: Numéro spécial consacré à l'Exposition de la "Section d'Or", ежегодная премьера, № 1, 9 октября 1912 г., стр. 1–7. Архивировано в 2020 г. - 10-30 в Wayback Machine , Библиотека Кандинского.
- ^ Герц-Фишлер, Роджер (1983). «Исследование утверждений относительно Сёра и золотого числа» (PDF) . Gazette des Beaux-Arts . 101 : 109–112.
- ^ Герберт, Роберт (1968). Неоимпрессионизм . Фонд Гуггенхайма. стр. 24.
- ^ Ливио 2002, стр. 169.
- ^ ab Camfield, William A. (март 1965). «Хуан Грис и золотое сечение». The Art Bulletin . 47 (1): 128–134. doi :10.1080/00043079.1965.10788819.
- ^ Грин, Кристофер (1992). Хуан Грис . Йель. стр. 37–38. ISBN 9780300053746.
Коттингтон, Дэвид (2004). Кубизм и его история. Manchester University Press. С. 112, 142.
- ^ Аллард, Роджер (июнь 1911 г.). «Sur quelques peintres». Les Marches du Sud-Ouest : 57–64.Перепечатано в Antliff, Mark; Leighten, Patricia, eds. (2008). A Cubism Reader, Documents and Criticism, 1906–1914. Издательство Чикагского университета. С. 178–191.
- ^ Було, Чарльз (1963). Секретная геометрия художника: исследование композиции в искусстве. Harcourt, Brace & World. стр. 247–248.
- ↑ Ливио 2002, стр. 177–178.
Цитируемые работы
- Герц-Фишлер, Роджер (1998) [1987]. Математическая история золотого числа . Дувр. ISBN 9780486400075.(Первоначально название «Математическая история деления в крайнем и среднем отношении ».)
- Ливио, Марио (2002). Золотое сечение: История Фи, самого удивительного числа в мире . Нью-Йорк: Broadway Books. ISBN 9780767908153.
- Посаментье, Альфред С.; Леманн, Ингмар (2011). Великолепное золотое сечение. Книги Прометея . ISBN 9-781-61614-424-1.
Дальнейшее чтение
- Доци, Дьёрдь (1981). Сила пределов: пропорциональные гармонии в природе, искусстве и архитектуре . Бостон: Шамбала.
- Харгиттай, Иштван, изд. (1992). Пятикратная симметрия . Всемирная научная. ISBN 9789810206000.
- Хантли, Х. Э. (1970). Божественная пропорция: исследование математической красоты . Нью-Йорк: Довер. ISBN 978-0-486-22254-7.
- Шааф, Уильям Л., ред. (1967). Золотая мера (PDF) . Серия переизданий Калифорнийской школьной группы по математике. Стэнфордский университет. Архивировано (PDF) из оригинала 25.04.2015.
- Ссимоне, Альдо (1997). Ла Сеционе Ауреа. Культурная история лейтмотивов математики . Палермо: Sigma Edizioni. ISBN 978-88-7231-025-0.
- Вальзер, Ганс (2001) [ Der Goldene Schnitt 1993]. Золотое сечение . Питер Хилтон пер. Вашингтон, округ Колумбия: Математическая ассоциация Америки. ISBN 978-0-88385-534-8.
Внешние ссылки
- Вайсштейн, Эрик В. «Золотое сечение». Математический мир .
- Богомольный, Александр (2018). «Золотое сечение в геометрии». Cut-the-Knot .
- Нотт, Рон. «Золотое сечение: Фи».Информация и деятельность профессора математики.
- Миф, который не исчезнет. Архивировано 12 ноября 2020 г. на Wayback Machine . Автор — Кит Девлин . В статье рассматриваются многочисленные обвинения в использовании золотого сечения в культуре.
- Ложные золотые спирали, собранные Рэндаллом Манро
- Лекция на YouTube о задаче Зенона о мышах и логарифмических спиралях








































![{\displaystyle {\begin{aligned}\varphi ^{2}&=\varphi +1=2.618033\dots ,\\[5mu]{\frac {1}{\varphi }}&=\varphi -1=0.618033 \dots .\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ff2e5225abf67548cf93c882add3a4b439c4aeb8)






![{\displaystyle {\begin{aligned}\varphi ^{n}&=\varphi ^{n-1}+\varphi ^{n-3}+\cdots +\varphi ^{n-1-2m}+\ varphi ^{n-2-2m}\\[5mu]\varphi ^{n}-\varphi ^{n-1}&=\varphi ^{n-2}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/048f09b7012c7fbd3d9f32798de6dd5c01acabcd)

![{\displaystyle \varphi =[1;1,1,1,\dots ]=1+{\cfrac {1}{1+{\cfrac {1}{1+{\cfrac {1}{1+\ddots }}}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/95682588ffee3530627c3a7b00ff08bbba6e97d4)
![{\displaystyle \varphi ^{-1}=[0;1,1,1,\dots ]=0+{\cfrac {1}{1+{\cfrac {1}{1+{\cfrac {1}{1+\ddots }}}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/165d255e32f4b9af1f9144f15302b147fc3fead2)























































![{\displaystyle {\begin{aligned}3\varphi ^{3}-5\varphi ^{2}+4&=3(\varphi ^{2}+\varphi )-5\varphi ^{2}+4\ \[5mu]&=3[(\varphi +1)+\varphi ]-5(\varphi +1)+4\\[5mu]&=\varphi +2\approx 3.618033.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/60ff8508aa117064d60142d447fb0cb58a809848)


![{\displaystyle {\begin{align}\varphi ^{0}&=1,\\[5mu]\varphi ^{1}&=1,618033989\ldots \approx 2,\\[5mu]\varphi ^{2}&=2,618033989\ldots \approx 3,\\[5mu]\varphi ^{3}&=4,236067978\ldots \approx 4,\\[5mu]\varphi ^{4}&=6,854101967\ldots \approx 7,\end{align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c4ac9ddf7e52ee6d1d0976b18e49ea4a99375dee)



























![{\displaystyle {\begin{aligned}{\frac {2\pi -g}{g}} &={\frac {2\pi }{2\pi -g}}=\varphi ,\\[8mu] 2\pi -g&={\frac {2\pi }{\varphi }}\approx 222,5^{\circ },\\[8mu]g&={\frac {2\pi }{\varphi ^{2}}}\approx 137,5^{\circ }.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fd5f9122b38d09e0cd2992820f27b8587efd167a)





![{\displaystyle {\begin{aligned}\varphi &=1+2\sin(\pi /10)=1+2\sin 18^{\circ },\\[5mu]\varphi &={\tfrac { 1}{2}}\csc(\pi /10)={\tfrac {1}{2}}\csc 18^{\circ },\\[5mu]\varphi &=2\cos(\pi /5)=2\cos 36^{\circ },\\[5mu]\varphi &=2\sin(3\pi /10)=2\sin 54^{\circ }.\end{выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0c42bbf25d6257a00fad895691aa2c5eb0c6f57a)





![{\displaystyle {\begin{aligned}A&={\tfrac {s^{2}}{2}}{\sqrt {\varphi }},\\[5mu]\theta &=\sin ^{-1}{\frac {1}{\varphi }}\approx 38.1727^{\circ },\\[5mu]\theta &=\cos ^{-1}{\frac {1}{\varphi }}\approx 51.8273^{\circ }.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f96fa323a2e180a6198f05d33c13e1631854e840)
![{\displaystyle {\begin{align}\alpha &=2\arctan {1 \over \varphi }\approx 63.43495^{\circ },\\[5mu]\beta &=2\arctan \varphi =\pi -\arctan 2=\arctan 1+\arctan 3\approx 116.56505^{\circ }.\end{align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7c5a4321454f4ca1b41b0dbd8f2c6c4afd48467e)


![{\displaystyle {\begin{aligned}d&={2a \over {\sqrt {2+\varphi }}}=2{\sqrt {{3-\varphi } \over 5}}a\approx 1.05146a,\\[5mu]D&=2{\sqrt {{2+\varphi } \over 5}}a\approx 1.70130a.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d00bbc42679ab9e34fdf849ac68de75180cc92c7)
![{\displaystyle {\begin{aligned}A&=(\sin(\arctan 2))~a^{2}={2 \over {\sqrt {5}}}~a^{2}\approx 0.89443a^{2},\\[5mu]A&={{\varphi } \over 2}d^{2}\approx 0.80902d^{2}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7bed70dcf23f16f3f8241aeaf2b56f0897244ff3)







































![{\textstyle \mathbb {Z} [\varphi].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6c19ab3d8278828be7f591bad1dc4482e4aaac6d)
![{\displaystyle {\begin{aligned}e^{0}+e^{-0}&=2,\\[5mu]e^{2\pi i/5}+e^{-2\pi i/ 5}&=\varphi ^{-1}=-1+\varphi ,\\[5mu]e^{4\pi i/5}+e^{-4\pi i/5}&=-\varphi .\end{выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bec7bcbd2e99aef0874eb163966c3e2dd9424b86)

![{\displaystyle {\begin{aligned}e^{\pi i}+e^{-\pi i}&=-2,\\[5mu]e^{\pi i/5}+e^{-\ pi i/5}&=\varphi ,\\[5mu]e^{3\pi i/5}+e^{-3\pi i/5}&=-\varphi ^{-1}=1- \варфи .\end{выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9459634b32b6990a97eb560ce696a3bc2e722513)




![{\displaystyle \mathbb {Z} [\varphi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/14f984c2710477c64fca0f16a71928134bdb8201)














![{\displaystyle {\begin{aligned}{\Bigl (}\varphi +R {{\bigl (}e^{-2a}{\bigr )}}{\Bigr )}{\Bigl (}\varphi +R {{\bigl (}e^{-2b}{\bigr )}}{\Bigr )}&=\varphi {\sqrt {5}},\\[5mu]{\Bigl (}\varphi ^{-1}-R{{\bigl (}{-e^{-a}}{\bigr )}}{\Bigr )} {\Bigl (}\varphi ^{-1}-R{{\bigl (}{-e^{-b}}{\bigr )}}{\Bigr )}&=\varphi ^{-1}{\sqrt {5}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/efa72855991c37845330a894d36b1d91647a265a)
















