Тетрагептагональная мозаика

Тетрагептагональная мозаика
Модель диска Пуанкаре гиперболической плоскости
Тип	Гиперболическая однородная мозаика
Конфигурация вершины	(4.7) 2
Символ Шлефли	г{7,4} или рр{7,7}${\displaystyle {\begin{Bmatrix}7\\4\end{Bmatrix}}}$
Символ Витхоффа	2 | 7 4 7 7 | 2
Диаграмма Коксетера
Группа симметрии	[7,4], (*742) [7,7], (*772)
Двойной	Заказ-7-4 ромбовидная мозаика
Характеристики	Вершинно-транзитивный, ребро-транзитивный

В геометрии тетрагептагональная мозаика — это однородная мозаика гиперболической плоскости . Она имеет символ Шлефли r{4,7}.

Существует конструкция с половинной симметрией [1+,4,7] = [7,7], которую можно рассматривать как два цвета семиугольников. Эту раскраску можно назвать ромбогептагептагональной мозаикой .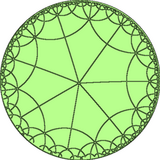

Двойная мозаика состоит из ромбических граней и имеет конфигурацию граней V4.7.4.7.

* n 42 мутации симметрии квазирегулярных мозаик: (4. n ) 2 в т е
Симметрия *4 n 2 [n,4]	Сферический	Евклидов	Компактный гиперболический				Паракомпактный	Некомпактный
	*342 [3,4]	*442 [4,4]	*542 [5,4]	*642 [6,4]	*742 [7,4]	*842 [8,4]...	*∞42 [∞,4]	[ н я,4]
Цифры
Конфигурация.	(4.3) 2	(4.4) 2	(4,5) 2	(4.6) 2	(4.7)2	(4,8) 2	(4.∞)2	(4. н я) 2

Однородные семиугольные/квадратные мозаики в т е
Симметрия: [7,4], (*742)							[7,4] + , (742)	[7 + ,4], (7*2)	[7,4,1 + ], (*772)
{7,4}	т{7,4}	г{7,4}	2т{7,4}=т{4,7}	2r{7,4}={4,7}	рр{7,4}	тр{7,4}	ср{7,4}	с{7,4}	ч{4,7}
Равномерные дуалы
В7 4	В4.14.14	В4.7.4.7	В7.8.8	В4 7	В4.4.7.4	В4.8.14	В3.3.4.3.7	В3.3.7.3.7	В7 7

Однородные гептагептагональные мозаики в т е
Симметрия: [7,7], (*772)							[7,7] + , (772)
= =	= =	= =	= =	= =	= =	= =	= =
{7,7}	т{7,7}	г{7,7}	2т{7,7}=т{7,7}	2r{7,7}={7,7}	рр{7,7}	тр{7,7}	ср{7,7}
Равномерные дуалы
В7 7	В7.14.14	В7.7.7.7	В7.14.14	В7 7	В4.7.4.7	В4.14.14	В3.3.7.3.7

Размерное семейство квазиправильных многогранников и мозаик: (7. n ) 2 в т е
Симметрия *7n2 [n,7]	Гиперболический...						Паракомпактный	Некомпактный
	*732 [3,7]	*742 [4,7]	*752 [5,7]	*762 [6,7]	*772 [7,7]	*872 [8,7]...	*∞72 [∞,7]	[iπ/λ,7]
Коксетер
Конфигурация квазирегулярных фигур	3.7.3.7	4.7.4.7	7.5.7.5	7.6.7.6	7.7.7.7	7.8.7.8	7.∞.7.∞	7.∞.7.∞

На Викискладе есть медиафайлы по теме « Однородная мозаика 4-7-4-7» .

• Однородные мозаики на гиперболической плоскости
• Список правильных многогранников

• Джон Х. Конвей , Хайди Бергиел, Хаим Гудман-Штраус, Симметрии вещей 2008, ISBN  978-1-56881-220-5 (Глава 19, Гиперболические архимедовы мозаики)
• "Глава 10: Регулярные соты в гиперболическом пространстве". Красота геометрии: Двенадцать эссе . Dover Publications. 1999. ISBN 0-486-40919-8. LCCN  99035678.

• Вайсштейн, Эрик В. "Гиперболическая мозаика". MathWorld .
• Вайсштейн, Эрик В. "Гиперболический диск Пуанкаре". MathWorld .
• Галерея гиперболических и сферических мозаик
• KaleidoTile 3: Образовательное программное обеспечение для создания сферических, плоских и гиперболических мозаик
• Гиперболические плоские мозаики, Дон Хэтч

Эта статья, связанная с гиперболической геометрией, является заглушкой . Вы можете помочь Википедии, расширив ее.

• в
• т
• е