Стерилизованные 6-ортоплексы
 6-ортоплекс            |  Стерилизованный 6-ортоплекс            |  Стери-усеченный 6-ортоплекс            |
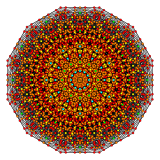 Стерилизованный 6-ортоплекс            |  Стерикантитруцированный 6-ортоплекс            |  Стерилизованный 6-ортоплекс            |
 Стерилизованный усеченный 6-ортоплекс            |  Стерилизованный 6-ортоплекс            |  Стерирунцикантитрированный 6-ортоплекс            |
| Ортогональные проекции в плоскости Коксетера B 6 | ||
|---|---|---|
В шестимерной геометрии стерифицированный 6-ортоплекс представляет собой выпуклый однородный 6-многогранник , построенный как стерификация (усечение 4-го порядка) правильного 6-ортоплекса .
Существует 16 уникальных стерикаций для 6-ортоплекса с перестановками усечений, кантелляций и рунцинаций. Восемь лучше представлены из стерикованного 6-куба .
Стерилизованный 6-ортоплекс
| Стерилизованный 6-ортоплекс | |
|---|---|
| Тип | однородный 6-многогранник |
| Символ Шлефли | 2р2р{3,3,3,3,4} |
| Диаграммы Коксетера-Дынкина |                   |
| 5-гранный | |
| 4-х гранный | |
| Клетки | |
| Лица | |
| Края | 5760 |
| Вершины | 960 |
| Вершинная фигура | |
| Группы Коксетера | В 6 , [4,3,3,3,3] |
| Характеристики | выпуклый |
Альтернативные названия
- Мелкоклеточный гексаконтатетрапетон (сокращение: scag) (Джонатан Бауэрс) [1]
Изображения
| самолет Коксетера | Б 6 | Б 5 | Б 4 |
|---|---|---|---|
| График |  |  |  |
| Диэдральная симметрия | [12] | [10] | [8] |
| самолет Коксетера | Б 3 | Б 2 | |
| График |  |  | |
| Диэдральная симметрия | [6] | [4] | |
| самолет Коксетера | А 5 | А 3 | |
| График |  |  | |
| Диэдральная симметрия | [6] | [4] |
Стери-усеченный 6-ортоплекс
| Стери-усеченный 6-ортоплекс | |
|---|---|
| Тип | однородный 6-многогранник |
| Символ Шлефли | т 0,1,4 {3,3,3,3,4} |
| Диаграммы Коксетера-Дынкина |            |
| 5-гранный | |
| 4-х гранный | |
| Клетки | |
| Лица | |
| Края | 19200 |
| Вершины | 3840 |
| Вершинная фигура | |
| Группы Коксетера | В 6 , [4,3,3,3,3] |
| Характеристики | выпуклый |
Альтернативные названия
- Целлиукороченный гексаконтатетрапетон (Акроним: catog) (Джонатан Бауэрс) [2]
Изображения
| самолет Коксетера | Б 6 | Б 5 | Б 4 |
|---|---|---|---|
| График |  |  |  |
| Диэдральная симметрия | [12] | [10] | [8] |
| самолет Коксетера | Б 3 | Б 2 | |
| График |  |  | |
| Диэдральная симметрия | [6] | [4] | |
| самолет Коксетера | А 5 | А 3 | |
| График |  |  | |
| Диэдральная симметрия | [6] | [4] |
Стерилизованный 6-ортоплекс
| Стерилизованный 6-ортоплекс | |
|---|---|
| Тип | однородный 6-многогранник |
| Символы Шлефли | т 0,2,4 {3 4 ,4} rr2r{3,3,3,3,4} |
| Диаграммы Коксетера-Дынкина |                   |
| 5-гранный | |
| 4-х гранный | |
| Клетки | |
| Лица | |
| Края | 28800 |
| Вершины | 5760 |
| Вершинная фигура | |
| Группы Коксетера | В 6 , [4,3,3,3,3] |
| Характеристики | выпуклый |
Альтернативные названия
- Целлиромбатированный гексаконтатетрапетон (сокращение: скала) (Джонатан Бауэрс) [3]
Изображения
| самолет Коксетера | Б 6 | Б 5 | Б 4 |
|---|---|---|---|
| График |  |  |  |
| Диэдральная симметрия | [12] | [10] | [8] |
| самолет Коксетера | Б 3 | Б 2 | |
| График |  |  | |
| Диэдральная симметрия | [6] | [4] | |
| самолет Коксетера | А 5 | А 3 | |
| График |  |  | |
| Диэдральная симметрия | [6] | [4] |
Стерикантитруцированный 6-ортоплекс
| Стерикантитруцированный 6-ортоплекс | |
|---|---|
| Тип | однородный 6-многогранник |
| Символ Шлефли | т 0,1,2,4 {3,3,3,3,4} |
| Диаграммы Коксетера-Дынкина |            |
| 5-гранный | |
| 4-х гранный | |
| Клетки | |
| Лица | |
| Края | 46080 |
| Вершины | 11520 |
| Вершинная фигура | |
| Группы Коксетера | В 6 , [4,3,3,3,3] |
| Характеристики | выпуклый |
Альтернативные названия
- Целлигреаторомбатированный гексаконтатетрапетон (сокращение: cagorg) (Джонатан Бауэрс) [4]
Изображения
| самолет Коксетера | Б 6 | Б 5 | Б 4 |
|---|---|---|---|
| График |  |  |  |
| Диэдральная симметрия | [12] | [10] | [8] |
| самолет Коксетера | Б 3 | Б 2 | |
| График |  |  | |
| Диэдральная симметрия | [6] | [4] | |
| самолет Коксетера | А 5 | А 3 | |
| График |  |  | |
| Диэдральная симметрия | [6] | [4] |
Стерилизованный 6-ортоплекс
| Стерилизованный 6-ортоплекс | |
|---|---|
| Тип | однородный 6-многогранник |
| Символ Шлефли | т 0,3,4 {3,3,3,3,4} |
| Диаграммы Коксетера-Дынкина |            |
| 5-гранный | |
| 4-х гранный | |
| Клетки | |
| Лица | |
| Края | 15360 |
| Вершины | 3840 |
| Вершинная фигура | |
| Группы Коксетера | В 6 , [4,3,3,3,3] |
| Характеристики | выпуклый |
Альтернативные названия
- Целлипризмированный гексаконтатетрапетон (сокращение: copog) (Джонатан Бауэрс) [5]
Изображения
| самолет Коксетера | Б 6 | Б 5 | Б 4 |
|---|---|---|---|
| График |  |  |  |
| Диэдральная симметрия | [12] | [10] | [8] |
| самолет Коксетера | Б 3 | Б 2 | |
| График |  |  | |
| Диэдральная симметрия | [6] | [4] | |
| самолет Коксетера | А 5 | А 3 | |
| График |  |  | |
| Диэдральная симметрия | [6] | [4] |
Стерилизованный усеченный 6-ортоплекс
| Стерилизованный усеченный 6-ортоплекс | |
|---|---|
| Тип | однородный 6-многогранник |
| Символ Шлефли | 2т2р{3,3,3,3,4} |
| Диаграммы Коксетера-Дынкина |                   |
| 5-гранный | |
| 4-х гранный | |
| Клетки | |
| Лица | |
| Края | 40320 |
| Вершины | 11520 |
| Вершинная фигура | |
| Группы Коксетера | В 6 , [4,3,3,3,3] |
| Характеристики | выпуклый |
Альтернативные названия
- Целлиприсмоусечённый гексаконтатетрапетон (сокращение: captog) (Джонатан Бауэрс) [6]
Изображения
| самолет Коксетера | Б 6 | Б 5 | Б 4 |
|---|---|---|---|
| График |  |  |  |
| Диэдральная симметрия | [12] | [10] | [8] |
| самолет Коксетера | Б 3 | Б 2 | |
| График |  |  | |
| Диэдральная симметрия | [6] | [4] | |
| самолет Коксетера | А 5 | А 3 | |
| График |  |  | |
| Диэдральная симметрия | [6] | [4] |
Стерилизованный 6-ортоплекс
| Стерилизованный 6-ортоплекс | |
|---|---|
| Тип | однородный 6-многогранник |
| Символ Шлефли | т 0,2,3,4 {3,3,3,3,4} |
| Диаграммы Коксетера-Дынкина |            |
| 5-гранный | |
| 4-х гранный | |
| Клетки | |
| Лица | |
| Края | 40320 |
| Вершины | 11520 |
| Вершинная фигура | |
| Группы Коксетера | В 6 , [4,3,3,3,3] |
| Характеристики | выпуклый |
Альтернативные названия
- Целлипризматоромбатированный гексаконтатетрапетон (Акроним: копраг) (Джонатан Бауэрс) [7]
Изображения
| самолет Коксетера | Б 6 | Б 5 | Б 4 |
|---|---|---|---|
| График |  |  |  |
| Диэдральная симметрия | [12] | [10] | [8] |
| самолет Коксетера | Б 3 | Б 2 | |
| График |  |  | |
| Диэдральная симметрия | [6] | [4] | |
| самолет Коксетера | А 5 | А 3 | |
| График |  |  | |
| Диэдральная симметрия | [6] | [4] |
Стерирунцикантитрированный 6-ортоплекс
| Стериунцикантиусеченный 6-ортоплекс | |
|---|---|
| Тип | однородный 6-многогранник |
| Символы Шлефли | т 0,1,2,3,4 {3 4 ,4} тр2р{3,3,3,3,4} |
| Диаграммы Коксетера-Дынкина |                   |
| 5-гранный | 536: 12 т 0,1,2,3 {3,3,3,4}  60 {}×t 0,1,2 {3,3,4}  × × 160 {6}×t 0,1,2 {3,3}  × × 240 {4}×t 0,1,2 {3,3}  × × 64 т 0,1,2,3,4 {3 4 }  |
| 4-х гранный | 8216 |
| Клетки | 38400 |
| Лица | 76800 |
| Края | 69120 |
| Вершины | 23040 |
| Вершинная фигура | нерегулярный 5-симплекс |
| Группы Коксетера | В 6 , [4,3,3,3,3] |
| Характеристики | выпуклый |
Альтернативные названия
- Большой ячеистый гексаконтатетрапетон (сокращение: gocog) (Джонатан Бауэрс) [8]
Изображения
| самолет Коксетера | Б 6 | Б 5 | Б 4 |
|---|---|---|---|
| График |  | 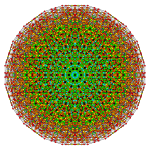 |  |
| Диэдральная симметрия | [12] | [10] | [8] |
| самолет Коксетера | Б 3 | Б 2 | |
| График |  |  | |
| Диэдральная симметрия | [6] | [4] | |
| самолет Коксетера | А 5 | А 3 | |
| График |  |  | |
| Диэдральная симметрия | [6] | [4] |
Курносый 6-демикуб
Плосконосый 6-демикуб, определяемый как чередование усеченного 6-демикуба, не является однородным, но ему можно придать диаграмму Коксетера







 или
или









 и симметрия [3 2,1,1,1 ] + или [4,(3,3,3,3) + ], и построены из 12 плосконосых 5-демикубов , 64 плосконосых 5-симплексов , 60 плосконосых 24-ячеечных антипризм, 160 3-s{3,4} дуоантипризм, 240 2-sr{3,3} дуоантипризм и 11520 неправильных 5-симплексов, заполняющих пробелы в удаленных вершинах.
и симметрия [3 2,1,1,1 ] + или [4,(3,3,3,3) + ], и построены из 12 плосконосых 5-демикубов , 64 плосконосых 5-симплексов , 60 плосконосых 24-ячеечных антипризм, 160 3-s{3,4} дуоантипризм, 240 2-sr{3,3} дуоантипризм и 11520 неправильных 5-симплексов, заполняющих пробелы в удаленных вершинах.
Связанные многогранники
Эти многогранники входят в набор из 63 однородных 6-мерных многогранников, сгенерированных из плоскости Коксетера B 6 , включая правильный 6-ортоплекс или 6-ортоплекс .
Примечания
- ^ Клитцинг, (x3o3o3o3x4o - скаг)
- ^ Клитцинг, (x3x3o3o3x4o - catog)
- ^ Клитцинг, (x3o3x3o3x4o - скала)
- ^ Клитцинг, (x3x3x3o3x4o - cagorg)
- ^ Клитцинг, (x3o3o3x3x4o - копог)
- ^ Клитцинг, (x3x3o3x3x4o - captog)
- ^ Клитцинг, (x3o3x3x3x4o - копраг)
- ^ Клитцинг, (x3x3x3x3x4o - gocog)
Ссылки
- HSM Коксетер :
- HSM Coxeter, Правильные многогранники , 3-е издание, Довер, Нью-Йорк, 1973 г.
- Калейдоскопы: избранные труды Х. С. М. Коксетера , под редакцией Ф. Артура Шерка, Питера МакМаллена, Энтони К. Томпсона, Азии Айвик Вайс, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
- (Документ 22) HSM Coxeter, Правильные и полуправильные многогранники I , [Math. Zeit. 46 (1940) 380–407, MR 2,10]
- (Документ 23) HSM Coxeter, Правильные и полуправильные многогранники II , [Math. Zeit. 188 (1985) 559-591]
- (Документ 24) HSM Coxeter, Правильные и полуправильные многогранники III , [Math. Zeit. 200 (1988) 3-45]
- Норман Джонсон Однородные многогранники , Рукопись (1991)
- Н. В. Джонсон: Теория однородных многогранников и сот , доктор философии.
- Клитцинг, Ричард. «6D однородные многогранники (полипеты)».
Внешние ссылки
- Многогранники различных размерностей
- Многомерный глоссарий






























































