Трение

| Часть серии статей о |
| Классическая механика |
|---|

Трение — это сила , сопротивляющаяся относительному движению твердых поверхностей, слоев жидкости и материальных элементов, скользящих друг по другу. [2] [3] Типы трения включают сухое, жидкостное, смазанное, поверхностное и внутреннее — неполный список. Изучение вовлеченных процессов называется трибологией и имеет историю более 2000 лет. [4]
Трение может иметь драматические последствия, как показано на примере использования трения, создаваемого трением кусков дерева друг о друга для разжигания огня . Другим важным последствием многих типов трения может быть износ , который может привести к ухудшению производительности или повреждению компонентов. Известно, что потери энергии на трение составляют около 20% от общего расхода энергии в мире. [5] [6]
Как кратко обсуждается ниже, существует много различных факторов, вносящих вклад в силу торможения при трении, начиная от деформации неровностей и заканчивая генерацией зарядов и изменениями в локальной структуре . Трение само по себе не является фундаментальной силой , это неконсервативная сила — работа, совершаемая против трения, зависит от пути. При наличии трения часть механической энергии преобразуется в тепло , а также в свободную энергию структурных изменений и других типов рассеивания , поэтому механическая энергия не сохраняется. Сложность вовлеченных взаимодействий затрудняет расчет трения из первых принципов , и часто проще использовать эмпирические методы для анализа и разработки теории. [3] [2]
Типы
Существует несколько видов трения:
- Сухое трение — это сила, которая противодействует относительному боковому движению двух твердых поверхностей, находящихся в контакте. Сухое трение подразделяется на статическое трение (« липкость ») между неподвижными поверхностями и кинетическое трение между движущимися поверхностями. За исключением атомного или молекулярного трения, сухое трение обычно возникает из-за взаимодействия поверхностных особенностей, известных как неровности (см. рисунок).
- Жидкостное трение описывает трение между слоями вязкой жидкости, которые движутся относительно друг друга. [7] [8]
- Смазочное трение — это случай жидкостного трения, когда смазочная жидкость разделяет две твердые поверхности. [9] [10] [11]
- Поверхностное трение является компонентом сопротивления — силы, противодействующей движению жидкости по поверхности тела.
- Внутреннее трение — это сила, противодействующая движению между элементами, составляющими твердый материал, при его деформации . [8] [4]
История
Многие древние авторы, включая Аристотеля , Витрувия и Плиния Старшего , интересовались причиной и уменьшением трения. [12] Они знали о различиях между статическим и кинетическим трением, а Фемистий в 350 году нашей эры утверждал , что «легче способствовать движению движущегося тела, чем двигать тело, находящееся в состоянии покоя». [12] [13] [14] [15]
Классические законы трения скольжения были открыты Леонардо да Винчи в 1493 году, пионером трибологии , но законы, задокументированные в его записных книжках, не были опубликованы и остались неизвестными. [16] [17] [18] [19] [20] [21] Эти законы были заново открыты Гийомом Амонтоном в 1699 году [22] и стали известны как три закона сухого трения Амонтона. Амонтон представил природу трения с точки зрения неровностей поверхности и силы, необходимой для подъема груза, прижимающего поверхности друг к другу. Эта точка зрения была далее развита Бернаром Форестом де Белидором [23] и Леонардом Эйлером (1750), которые вывели угол естественного откоса груза на наклонной плоскости и впервые провели различие между статическим и кинетическим трением. [24] Джон Теофил Дезагюлье (1734) первым осознал роль адгезии в трении. [25] Микроскопические силы заставляют поверхности слипаться; он предположил, что трение — это сила, необходимая для разрыва слипшихся поверхностей.
Понимание трения было далее развито Шарлем-Огюстеном де Кулоном (1785). [22] Кулон исследовал влияние четырех основных факторов на трение: природа контактирующих материалов и их поверхностных покрытий; размер площади поверхности; нормальное давление (или нагрузка); и продолжительность времени, в течение которого поверхности оставались в контакте (время покоя). [16] Кулон далее рассмотрел влияние скорости скольжения, температуры и влажности, чтобы сделать выбор между различными объяснениями природы трения, которые были предложены. Различие между статическим и динамическим трением проводится в законе трения Кулона (см. ниже), хотя это различие было уже проведено Иоганном Андреасом фон Сегнером в 1758 году. [16] Влияние времени покоя было объяснено Питером ван Мушенбруком (1762), рассматривая поверхности волокнистых материалов с волокнами, сцепленными вместе, что занимает конечное время, в течение которого трение увеличивается.
Джон Лесли (1766–1832) отметил слабость взглядов Амонтона и Кулона: если трение возникает из-за того, что груз поднимается по наклонной плоскости последовательных неровностей , то почему он не уравновешивается при спуске по противоположному склону? Лесли был столь же скептически настроен по отношению к роли адгезии, предложенной Дезагюлье, которая в целом должна иметь одинаковую тенденцию как к ускорению, так и к замедлению движения. [16] По мнению Лесли, трение следует рассматривать как зависящий от времени процесс сглаживания, придавливания неровностей, что создает новые препятствия в том, что раньше было полостями.
В ходе длительного развития закона сохранения энергии и первого закона термодинамики трение было признано способом преобразования механической работы в тепло . В 1798 году Бенджамин Томпсон сообщил об экспериментах по сверлению стволов пушек. [26]
Артур Жюль Морен (1833) разработал концепцию трения скольжения и качения.
В 1842 году Юлиус Роберт Майер вырабатывал тепло путем трения в бумажной массе и измерил повышение температуры. [27] В 1845 году Джоуль опубликовал статью под названием «Механический эквивалент тепла », в которой он указал численное значение количества механической работы, необходимой для «производства единицы тепла», основываясь на трении электрического тока, проходящего через резистор, и на трении лопастного колеса, вращающегося в чане с водой. [28]
Осборн Рейнольдс (1866) вывел уравнение вязкого течения. Это завершило классическую эмпирическую модель трения (статического, кинетического и жидкостного), которая сегодня широко используется в технике. [17] В 1877 году Флиминг Дженкин и Дж. А. Юинг исследовали непрерывность между статическим и кинетическим трением. [29]
В 1907 году GH Bryan опубликовал исследование основ термодинамики, Thermodynamics: an Introductory Treatise, посвященное в основном первым принципам и их прямым применениям . Он отметил, что для ведомой твердой поверхности, скользящей по телу, приводимому ею в движение, работа, выполняемая водителем, превышает работу, получаемую телом. Разница объясняется теплом, выделяемым трением. [30] На протяжении многих лет, например, в своей диссертации 1879 года, но особенно в 1926 году, Планк выступал за то, чтобы рассматривать генерацию тепла путем трения как наиболее конкретный способ определения тепла и яркий пример необратимого термодинамического процесса. [31]
Основное внимание в исследованиях 20-го века уделялось пониманию физических механизмов, лежащих в основе трения. Фрэнк Филип Боуден и Дэвид Табор (1950) показали, что на микроскопическом уровне фактическая площадь контакта между поверхностями составляет очень малую часть видимой площади. [18] Эта фактическая площадь контакта, вызванная неровностями, увеличивается с давлением. Разработка атомно-силового микроскопа (около 1986 г.) позволила ученым изучить трение в атомном масштабе , [17] показав, что в этом масштабе сухое трение является произведением межповерхностного напряжения сдвига и площади контакта. Эти два открытия объясняют первый закон Амонтона (ниже) ; макроскопическую пропорциональность между нормальной силой и статической силой трения между сухими поверхностями.
Законы сухого трения
Элементарные свойства трения скольжения (кинетического) были открыты экспериментально в XV–XVIII веках и выражены в виде трех эмпирических законов:
- Первый закон Амонтона : сила трения прямо пропорциональна приложенной нагрузке.
- Второй закон Амонтона : сила трения не зависит от видимой площади контакта.
- Закон трения Кулона : Кинетическое трение не зависит от скорости скольжения.
Сухое трение
Сухое трение противодействует относительному боковому движению двух твердых поверхностей, находящихся в контакте. Два режима сухого трения — это «статическое трение» (« прилипание ») между неподвижными поверхностями и кинетическое трение (иногда называемое трением скольжения или динамическим трением) между движущимися поверхностями.
Трение Кулона, названное в честь Шарля-Огюстена де Кулона , является приближенной моделью, используемой для расчета силы сухого трения. Она регулируется моделью: где
- это сила трения, оказываемая каждой поверхностью на другую. Она параллельна поверхности, в направлении, противоположном чистой приложенной силе.
- - коэффициент трения, который является эмпирическим свойством контактирующих материалов,
- это нормальная сила, действующая со стороны каждой поверхности на другую, направленная перпендикулярно (нормально) к поверхности.
Кулоновское трение может принимать любое значение от нуля до , а направление силы трения против поверхности противоположно движению, которое поверхность испытывала бы при отсутствии трения. Таким образом, в статическом случае сила трения является именно такой, какой она должна быть, чтобы предотвратить движение между поверхностями; она уравновешивает чистую силу, стремящуюся вызвать такое движение. В этом случае, вместо того чтобы предоставлять оценку фактической силы трения, приближение Кулона дает пороговое значение для этой силы, выше которого начнется движение. Эта максимальная сила известна как тяга .
Сила трения всегда действует в направлении, которое противодействует движению (для кинетического трения) или потенциальному движению (для статического трения) между двумя поверхностями. Например, скользящий по льду камень для керлинга испытывает кинетическую силу, замедляющую его. В качестве примера потенциального движения, ведущие колеса ускоряющегося автомобиля испытывают силу трения, направленную вперед; если бы они этого не делали, колеса вращались бы, а резина скользила бы назад по тротуару. Обратите внимание, что они противостоят не направлению движения транспортного средства, а направлению (потенциального) скольжения между шиной и дорогой.
Нормальная сила

Нормальная сила определяется как чистая сила, сжимающая две параллельные поверхности вместе, и ее направление перпендикулярно поверхностям. В простом случае массы, покоящейся на горизонтальной поверхности, единственным компонентом нормальной силы является сила тяжести, где . В этом случае условия равновесия говорят нам, что величина силы трения равна нулю , . Фактически, сила трения всегда удовлетворяет , причем равенство достигается только при критическом угле наклона (заданном ), который достаточно крут, чтобы инициировать скольжение.
Коэффициент трения — это эмпирическое (экспериментально измеренное) структурное свойство, которое зависит только от различных аспектов контактирующих материалов, таких как шероховатость поверхности. Коэффициент трения не является функцией массы или объема. Например, большой алюминиевый блок имеет тот же коэффициент трения, что и маленький алюминиевый блок. Однако величина самой силы трения зависит от нормальной силы и, следовательно, от массы блока.
В зависимости от ситуации, расчет нормальной силы может включать в себя силы, отличные от силы тяжести. Если объект находится на ровной поверхности и подвергается воздействию внешней силы, стремящейся заставить его скользить, то нормальная сила между объектом и поверхностью равна просто , где — вес блока, а — направленная вниз составляющая внешней силы. До скольжения эта сила трения равна , где — горизонтальная составляющая внешней силы. Таким образом, в общем случае. Скольжение начинается только после того, как эта сила трения достигает значения . До этого момента трение равно тому, что необходимо для обеспечения равновесия, поэтому его можно рассматривать просто как реакцию.
Если объект находится на наклонной поверхности , например, на наклонной плоскости, нормальная сила тяжести меньше, чем , поскольку меньшая часть силы тяжести перпендикулярна поверхности плоскости. Нормальная сила и сила трения в конечном итоге определяются с помощью векторного анализа, обычно с помощью диаграммы свободного тела .
В общем, процесс решения любой задачи статики с трением заключается в том, чтобы предварительно рассматривать контактирующие поверхности как неподвижные, чтобы можно было вычислить соответствующую тангенциальную силу реакции между ними. Если эта сила реакции трения удовлетворяет , то предварительное предположение было верным, и это фактическая сила трения. В противном случае силу трения следует установить равной , и тогда полученный дисбаланс сил определит ускорение, связанное со скольжением.
Коэффициент трения
![[icon]](http://upload.wikimedia.org/wikipedia/commons/thumb/1/1c/Wiki_letter_w_cropped.svg/20px-Wiki_letter_w_cropped.svg.png) | This section needs expansion with: explanation of why kinetic friction is always lower. You can help by making an edit requestadding to it . (August 2020) |
Коэффициент трения (COF), часто обозначаемый греческой буквой μ , представляет собой безразмерную скалярную величину, которая равна отношению силы трения между двумя телами и силы, прижимающей их друг к другу, либо во время, либо в начале скольжения. Коэффициент трения зависит от используемых материалов; например, лед на стали имеет низкий коэффициент трения, в то время как резина на тротуаре имеет высокий коэффициент трения. Коэффициенты трения варьируются от почти нуля до более чем единицы. Коэффициент трения между двумя поверхностями из одинаковых металлов больше, чем между двумя поверхностями из разных металлов; например, латунь имеет более высокий коэффициент трения при движении по латуни, но меньший при движении по стали или алюминию. [32]
Для поверхностей, находящихся в состоянии покоя относительно друг друга, , где - коэффициент статического трения . Он обычно больше, чем его кинетический аналог. Коэффициент статического трения, демонстрируемый парой контактирующих поверхностей, зависит от комбинированного воздействия характеристик деформации материала и шероховатости поверхности , оба из которых имеют свое происхождение в химической связи между атомами в каждом из объемных материалов и между поверхностями материала и любым адсорбированным материалом . Известно, что фрактальность поверхностей, параметр, описывающий масштабное поведение поверхностных неровностей, играет важную роль в определении величины статического трения. [1]
Для поверхностей, находящихся в относительном движении , где — коэффициент трения . Кулоновское трение равно , а сила трения на каждой поверхности действует в направлении, противоположном ее движению относительно другой поверхности.
Артур Морин ввел этот термин и продемонстрировал полезность коэффициента трения. [16] Коэффициент трения является эмпирическим измерением — его необходимо измерить экспериментально , и его нельзя найти с помощью расчетов. [33] Более шероховатые поверхности, как правило, имеют более высокие эффективные значения. Как статические, так и кинетические коэффициенты трения зависят от пары поверхностей в контакте; для данной пары поверхностей коэффициент статического трения обычно больше , чем кинетического трения; в некоторых наборах эти два коэффициента равны, например, тефлон-по-тефлону.
Большинство сухих материалов в сочетании имеют коэффициент трения между 0,3 и 0,6. Значения вне этого диапазона встречаются реже, но тефлон , например, может иметь коэффициент всего лишь 0,04. Значение, равное нулю, будет означать полное отсутствие трения, неуловимое свойство. Резина в контакте с другими поверхностями может давать коэффициент трения от 1 до 2. Иногда утверждается, что μ всегда < 1, но это не так. В то время как в большинстве соответствующих приложений μ < 1, значение выше 1 просто означает, что сила, необходимая для скольжения объекта по поверхности, больше нормальной силы поверхности на объекте. Например, поверхности, покрытые силиконовой резиной или акриловой резиной, имеют коэффициент трения, который может быть существенно больше 1.
Хотя часто утверждается, что COF является «свойством материала», его лучше отнести к категории «свойство системы». В отличие от истинных свойств материала (таких как проводимость, диэлектрическая проницаемость, предел текучести), COF для любых двух материалов зависит от системных переменных, таких как температура , скорость , атмосфера , а также от того, что сейчас обычно описывается как время старения и дестарения; а также от геометрических свойств интерфейса между материалами, а именно структуры поверхности . [1] Например, медный штифт, скользящий по толстой медной пластине, может иметь COF, который варьируется от 0,6 на низких скоростях (скольжение металла по металлу) до менее 0,2 на высоких скоростях, когда медная поверхность начинает плавиться из-за фрикционного нагрева. Последняя скорость, конечно, не определяет COF однозначно; если диаметр штифта увеличивается так, что фрикционный нагрев быстро устраняется, температура падает, штифт остается твердым, а COF повышается до значения испытания на «низкой скорости». [ необходима цитата ]
В системах со значительными неоднородными полями напряжений, поскольку локальное скольжение происходит до того, как система начнет скользить, макроскопический коэффициент статического трения зависит от приложенной нагрузки, размера или формы системы; закон Амонтона не выполняется макроскопически. [34]
Приблизительные коэффициенты трения
This section's factual accuracy is disputed. (November 2021) |
| Материалы | Трение покоя, | Кинетическое/скользящее трение, | |||
|---|---|---|---|---|---|
| Сухой и чистый. | Смазанный | Сухой и чистый. | Смазанный | ||
| Алюминий | Сталь | 0,61 [35] | 0,47 [35] | ||
| Алюминий | Алюминий | 1,05–1,35 [35] | 0,3 [35] | 1,4 [35] –1,5 [ необходима ссылка ] | |
| Золото | Золото | 2.5 [ требуется ссылка ] | |||
| Платина | Платина | 1.2 [35] | 0,25 [35] | 3.0 [ требуется ссылка ] | |
| Серебро | Серебро | 1.4 [35] | 0,55 [35] | 1.5 [ требуется ссылка ] | |
| Керамика из оксида алюминия | Керамика из нитрида кремния | 0,004 (влажный) [36] | |||
| БАМ (Керамический сплав AlMgB 14 ) | Борид титана ( TiB2 ) | 0,04–0,05 [37] | 0,02 [38] [39] | ||
| Латунь | Сталь | 0,35–0,51 [35] | 0,19 [35] | 0,44 [35] | |
| Чугун | Медь | 1.05 [35] | 0,29 [35] | ||
| Чугун | Цинк | 0,85 [35] | 0,21 [35] | ||
| Конкретный | Резина | 1.0 | 0,30 (мокрый) | 0,6–0,85 [35] | 0,45–0,75 (влажный) [35] |
| Конкретный | Древесина | 0,62 [35] [40] | |||
| Медь | Стекло | 0,68 [41] | 0,53 [41] | ||
| Медь | Сталь | 0,53 [41] | 0,36 [35] [41] | 0,18 [41] | |
| Стекло | Стекло | 0,9–1,0 [35] [41] | 0,005–0,01 [41] | 0,4 [35] [41] | 0,09–0,116 [41] |
| Синовиальная жидкость человека | Человеческий хрящ | 0,01 [42] | 0,003 [42] | ||
| Лед | Лед | 0,02–0,09 [43] | |||
| Полиэтилен | Сталь | 0,2 [35] [43] | 0,2 [35] [43] | ||
| ПТФЭ (тефлон) | ПТФЭ (тефлон) | 0,04 [35] [43] | 0,04 [35] [43] | 0,04 [35] | |
| Сталь | Лед | 0,03 [43] | |||
| Сталь | ПТФЭ (тефлон) | 0,04 [35] −0,2 [43] | 0,04 [35] | 0,04 [35] | |
| Сталь | Сталь | 0,74 [35] −0,80 [43] | 0,005–0,23 [41] [43] | 0,42–0,62 [35] [41] | 0,029–0,19 [41] |
| Древесина | Металл | 0,2–0,6 [35] [40] | 0,2 (мокрый) [35] [40] | 0,49 [41] | 0,075 [41] |
| Древесина | Древесина | 0,25–0,62 [35] [40] [41] | 0,2 (мокрый) [35] [40] | 0,32–0,48 [41] | 0,067–0,167 [41] |
При определенных условиях некоторые материалы имеют очень низкие коэффициенты трения. Примером является (высокоупорядоченный пиролитический) графит, который может иметь коэффициент трения ниже 0,01. [44] Этот режим сверхнизкого трения называется суперсмазкой .
Трение покоя
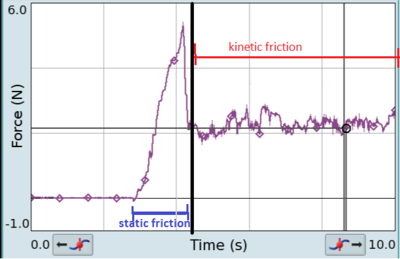
Статическое трение — это трение между двумя или более твердыми объектами, которые не движутся относительно друг друга. Например, статическое трение может предотвратить скольжение объекта по наклонной поверхности. Коэффициент статического трения, обычно обозначаемый как μ s , обычно выше коэффициента кинетического трения. Считается, что статическое трение возникает в результате особенностей шероховатости поверхности в нескольких масштабах длины на твердых поверхностях. Эти особенности, известные как неровности , присутствуют вплоть до наномасштабных размеров и приводят к истинному контакту твердого тела с твердым телом, существующему только в ограниченном количестве точек, что составляет лишь часть кажущейся или номинальной площади контакта. [45] Линейность между приложенной нагрузкой и истинной площадью контакта, возникающая из-за деформации неровностей, приводит к линейности между силой статического трения и нормальной силой, обнаруженной для типичного трения типа Амонтона–Кулона. [46]
Сила статического трения должна быть преодолена приложенной силой, прежде чем объект сможет двигаться. Максимально возможная сила трения между двумя поверхностями до начала скольжения является произведением коэффициента статического трения и нормальной силы: . Когда скольжения не происходит, сила трения может иметь любое значение от нуля до . Любой силе, меньшей, чем попытка скользить одной поверхностью по другой, противостоит сила трения равной величины и противоположного направления. Любая сила, большая, чем преодолевает силу статического трения и вызывает скольжение. Когда происходит мгновенное скольжение, статическое трение больше не применимо — трение между двумя поверхностями тогда называется кинетическим трением. Однако кажущееся статическое трение можно наблюдать даже в случае, когда истинное статическое трение равно нулю. [47]
Примером статического трения является сила, которая не дает колесу автомобиля скользить, когда оно катится по земле. Несмотря на то, что колесо находится в движении, участок шины, соприкасающийся с землей, неподвижен относительно земли, поэтому это статическое, а не кинетическое трение. При скольжении трение колеса меняется на кинетическое. Антиблокировочная тормозная система работает по принципу, позволяя заблокированному колесу возобновить вращение, так что автомобиль сохраняет статическое трение.
Максимальное значение статического трения, когда движение приближается, иногда называют предельным трением [48] , хотя этот термин не используется повсеместно. [7]
Кинетическое трение
Кинетическое трение , также известное как динамическое трение или трение скольжения , возникает, когда два объекта движутся относительно друг друга и трутся друг о друга (как сани по земле). Коэффициент кинетического трения обычно обозначается как μ k и обычно меньше коэффициента статического трения для тех же материалов. [49] [50] Однако Ричард Фейнман замечает, что «с сухими металлами очень трудно показать какую-либо разницу». [51] Сила трения между двумя поверхностями после начала скольжения является произведением коэффициента кинетического трения и нормальной силы: . Это отвечает за кулоновское затухание колеблющейся или вибрирующей системы.
Новые модели начинают показывать, как кинетическое трение может быть больше статического трения. [52] Во многих других случаях эффекты шероховатости являются доминирующими, например, при трении резины о дорогу. [52] Шероховатость поверхности и площадь контакта влияют на кинетическое трение для микро- и наномасштабных объектов, где силы поверхности доминируют над силами инерции. [53]
Происхождение кинетического трения в наномасштабе можно объяснить с помощью энергетической модели. [54] Во время скольжения новая поверхность образуется сзади скользящего истинного контакта, а существующая поверхность исчезает спереди. Поскольку все поверхности включают термодинамическую поверхностную энергию, работа должна быть затрачена на создание новой поверхности, а энергия выделяется в виде тепла при удалении поверхности. Таким образом, для перемещения задней части контакта требуется сила, а тепло трения выделяется спереди.

Угол трения
Для некоторых приложений более полезно определять статическое трение в терминах максимального угла, до которого один из предметов начнет скользить. Это называется углом трения или углом трения . Он определяется как: и таким образом: где — угол от горизонтали, а μ s — статический коэффициент трения между предметами. [55] Эту формулу также можно использовать для расчета μ s из эмпирических измерений угла трения.
Трение на атомном уровне
Определение сил, необходимых для перемещения атомов друг мимо друга, является сложной задачей при проектировании наномашин . В 2008 году ученые впервые смогли переместить один атом по поверхности и измерить необходимые силы. Используя сверхвысокий вакуум и почти нулевую температуру (5 К), модифицированный атомно-силовой микроскоп был использован для перемещения атома кобальта и молекулы оксида углерода по поверхностям меди и платины . [56]
Ограничения модели Кулона
Приближение Кулона следует из предположений, что: поверхности находятся в атомно тесном контакте только на небольшой части их общей площади; что эта площадь контакта пропорциональна нормальной силе (до насыщения, которое происходит, когда вся площадь находится в атомном контакте); и что сила трения пропорциональна приложенной нормальной силе, независимо от площади контакта. Приближение Кулона по сути является эмпирической конструкцией. Это эмпирическое правило, описывающее приблизительный результат чрезвычайно сложного физического взаимодействия. Сила приближения заключается в его простоте и универсальности. Хотя связь между нормальной силой и силой трения не является строго линейной (и поэтому сила трения не полностью независима от площади контакта поверхностей), приближение Кулона является адекватным представлением трения для анализа многих физических систем.
Когда поверхности соединены, кулоновское трение становится очень плохим приближением (например, клейкая лента сопротивляется скольжению даже при отсутствии нормальной силы или при отрицательной нормальной силе). В этом случае сила трения может сильно зависеть от площади контакта. Некоторые шины для дрэг-рейсинга являются липкими по этой причине. Однако, несмотря на сложность фундаментальной физики трения, эти соотношения достаточно точны, чтобы быть полезными во многих приложениях.
«Отрицательный» коэффициент трения
По состоянию на 2012 год [update]одно исследование продемонстрировало потенциал для эффективного отрицательного коэффициента трения в режиме низкой нагрузки , что означает, что уменьшение нормальной силы приводит к увеличению трения. Это противоречит повседневному опыту, в котором увеличение нормальной силы приводит к увеличению трения. [57] Об этом сообщалось в журнале Nature в октябре 2012 года и касалось трения, возникающего при перемещении иглы атомно-силового микроскопа по листу графена в присутствии адсорбированного графеном кислорода. [57]
Численное моделирование модели Кулона
Несмотря на то, что модель Кулона является упрощенной моделью трения, она полезна во многих приложениях численного моделирования , таких как многотельные системы и гранулированный материал . Даже ее самое простое выражение инкапсулирует фундаментальные эффекты прилипания и скольжения, которые требуются во многих прикладных случаях, хотя для эффективной численной интеграции механических систем с кулоновским трением и двусторонним или односторонним контактом необходимо разработать специальные алгоритмы. [58] [59] [60] [61] [62] Некоторые довольно нелинейные эффекты , такие как так называемые парадоксы Пенлеве , могут встречаться при кулоновском трении. [63]
Сухое трение и нестабильность
Сухое трение может вызывать несколько типов нестабильности в механических системах, которые демонстрируют стабильное поведение при отсутствии трения. [64] Эти нестабильности могут быть вызваны уменьшением силы трения с увеличением скорости скольжения, расширением материала из-за выделения тепла во время трения (термоупругая нестабильность) или чисто динамическими эффектами скольжения двух эластичных материалов (неустойчивость Адамса–Мартинса). Последние были первоначально обнаружены в 1995 году Джорджем Г. Адамсом и Жуаном Армениу Коррейя Мартинсом для гладких поверхностей [65] [66] и позднее были обнаружены на периодических шероховатых поверхностях. [67] В частности, считается, что динамические нестабильности, связанные с трением, ответственны за визг тормозов и «песню» стеклянной арфы , [68] [69] явления, которые включают прилипание и скольжение, моделируемые как падение коэффициента трения со скоростью. [70]
Практически важным случаем являются автоколебания струн смычковых инструментов, таких как скрипка , виолончель , шарманка , эрху и т. д.
Была обнаружена связь между сухим трением и флаттерной неустойчивостью в простой механической системе, [71] для получения более подробной информации посмотрите фильм, заархивированный 10 января 2015 г. на Wayback Machine .
Фрикционная нестабильность может привести к образованию новых самоорганизующихся структур (или «вторичных структур») на поверхности скольжения, таких как трибопленки, образующиеся на месте, которые используются для снижения трения и износа в так называемых самосмазывающихся материалах. [72]
Жидкостное трение
Жидкостное трение происходит между слоями жидкости , которые движутся относительно друг друга. Это внутреннее сопротивление потоку называется вязкостью . В повседневной жизни вязкость жидкости описывается как ее «густота». Таким образом, вода «жидкая», имеющая меньшую вязкость, в то время как мед «густой», имеющий большую вязкость. Чем менее вязкая жидкость, тем легче она деформируется или движется.
Все реальные жидкости (кроме сверхтекучих ) оказывают некоторое сопротивление сдвигу и поэтому являются вязкими. Для учебных и объяснительных целей полезно использовать концепцию невязкой жидкости или идеальной жидкости , которая не оказывает никакого сопротивления сдвигу и поэтому не является вязкой.
Смазанное трение
Смазанное трение — это случай жидкостного трения, когда жидкость разделяет две твердые поверхности. Смазка — это метод, используемый для уменьшения износа одной или обеих поверхностей, находящихся в непосредственной близости друг от друга и движущихся относительно друг друга, путем помещения между поверхностями вещества, называемого смазкой.
В большинстве случаев приложенная нагрузка переносится давлением, создаваемым внутри жидкости из-за вязкого сопротивления трения движению смазочной жидкости между поверхностями. Адекватная смазка обеспечивает плавную непрерывную работу оборудования, с небольшим износом и без чрезмерных напряжений или заеданий в подшипниках. Когда смазка выходит из строя, металлические или другие компоненты могут тереться друг о друга разрушительным образом, вызывая нагрев и, возможно, повреждение или отказ.
Трение кожи
Поверхностное трение возникает из-за взаимодействия жидкости с кожей тела и напрямую связано с площадью поверхности тела, которая контактирует с жидкостью. Поверхностное трение подчиняется уравнению сопротивления и растет пропорционально квадрату скорости.
Поверхностное трение вызывается вязким сопротивлением в пограничном слое вокруг объекта. Существует два способа уменьшить поверхностное трение: первый — придать движущемуся телу такую форму, чтобы был возможен плавный поток, как у аэродинамического профиля. Второй способ — уменьшить длину и поперечное сечение движущегося объекта настолько, насколько это практически осуществимо.
Внутреннее трение
Внутреннее трение — это сила, противодействующая движению между элементами, составляющими твердый материал, при его деформации .
Пластическая деформация твердых тел — это необратимое изменение внутренней молекулярной структуры объекта. Это изменение может быть вызвано либо (или обоими) приложенной силой, либо изменением температуры. Изменение формы объекта называется деформацией. Сила, вызывающая ее, называется напряжением .
Упругая деформация твердых тел — это обратимое изменение внутренней молекулярной структуры объекта. Напряжение не обязательно вызывает постоянное изменение. По мере возникновения деформации внутренние силы противодействуют приложенной силе. Если приложенное напряжение не слишком велико, эти противодействующие силы могут полностью противостоять приложенной силе, позволяя объекту принять новое состояние равновесия и вернуться к своей первоначальной форме, когда сила будет снята. Это известно как упругая деформация или эластичность.
Радиационное трение
Вследствие давления света Эйнштейн [73] в 1909 году предсказал существование «лучевого трения», которое будет препятствовать движению материи. Он писал: «излучение будет оказывать давление на обе стороны пластины. Силы давления, оказываемые на обе стороны, равны, если пластина находится в состоянии покоя. Однако, если она движется, больше излучения будет отражаться на поверхности, которая находится впереди во время движения (передняя поверхность), чем на задней поверхности. Действующая назад сила давления, оказываемая на переднюю поверхность, таким образом, больше силы давления, действующей на заднюю поверхность. Следовательно, как равнодействующая двух сил, остается сила, которая противодействует движению пластины и которая увеличивается со скоростью пластины. Мы будем кратко называть эту результирующую «лучевым трением».
Другие виды трения
Сопротивление качению
Сопротивление качению — это сила, которая сопротивляется качению колеса или другого круглого объекта по поверхности, вызванному деформациями объекта или поверхности. Обычно сила сопротивления качению меньше, чем та, которая связана с кинетическим трением. [74] Типичные значения коэффициента сопротивления качению составляют 0,001. [75] Одним из наиболее распространенных примеров сопротивления качению является движение шин автомобиля по дороге , процесс, который генерирует тепло и звук в качестве побочных продуктов. [76]
Торможение трением
Любое колесо, оснащенное тормозом , способно генерировать большую силу торможения, обычно для замедления и остановки транспортного средства или вращающегося механизма. Трение торможения отличается от трения качения, поскольку коэффициент трения качения мал, тогда как коэффициент трения торможения рассчитан на большой размер за счет выбора материалов для тормозных колодок .
Трибоэлектрический эффект
Трение двух материалов друг о друга может привести к переносу заряда, либо электронов, либо ионов. Энергия, необходимая для этого, способствует трению. Кроме того, скольжение может вызвать накопление электростатического заряда , что может быть опасно, если присутствуют легковоспламеняющиеся газы или пары. Когда статическое накопление разряжается, взрывы могут быть вызваны воспламенением горючей смеси.
Трение ремня
Трение ремня — это физическое свойство, наблюдаемое по силам, действующим на ремень, обернутый вокруг шкива, когда один конец тянут. Результирующее натяжение, которое действует на оба конца ремня, можно смоделировать с помощью уравнения трения ремня.
На практике теоретическое натяжение, действующее на ремень или веревку, рассчитанное по уравнению трения ремня, можно сравнить с максимальным натяжением, которое может выдержать ремень. Это помогает проектировщику такой установки узнать, сколько раз ремень или веревка должны быть обернуты вокруг шкива, чтобы предотвратить его проскальзывание. Альпинисты и парусные экипажи демонстрируют стандартные знания о трении ремня при выполнении основных задач.
Снижение
Устройства
Такие устройства, как колеса, шарикоподшипники , роликовые подшипники , а также воздушные подушки или другие типы жидкостных подшипников, могут преобразовать трение скольжения в гораздо меньший тип трения качения.
Многие термопластичные материалы, такие как нейлон , HDPE и PTFE, обычно используются в подшипниках с низким коэффициентом трения . Они особенно полезны, поскольку коэффициент трения падает с увеличением приложенной нагрузки. [77] Для улучшения износостойкости для тяжелых или критических подшипников обычно указываются марки с очень высоким молекулярным весом .
Смазочные материалы
Обычный способ уменьшения трения — использование смазки , например, масла, воды или консистентной смазки, которая помещается между двумя поверхностями, что часто значительно снижает коэффициент трения. Наука о трении и смазке называется трибологией . Технология смазочных материалов — это когда смазочные материалы смешиваются с применением науки, особенно для промышленных или коммерческих целей.
Суперсмазываемость, недавно обнаруженный эффект, наблюдался в графите : это существенное уменьшение трения между двумя скользящими объектами, приближающееся к нулевому уровню. Очень небольшое количество энергии трения все равно будет рассеиваться.
Смазочные материалы, преодолевающие трение, не всегда должны представлять собой жидкие турбулентные жидкости или порошкообразные твердые вещества, такие как графит и тальк ; акустическая смазка на самом деле использует звук в качестве смазки.
Другой способ уменьшить трение между двумя частями — наложить микромасштабную вибрацию на одну из частей. Это может быть синусоидальная вибрация, используемая при ультразвуковой резке, или вибрационный шум, известный как вибрация .
Энергия трения
Согласно закону сохранения энергии , никакая энергия не уничтожается из-за трения, хотя она может быть потеряна для рассматриваемой системы. Механическая энергия преобразуется в тепло. Скользящая хоккейная шайба останавливается, потому что трение преобразует ее кинетическую энергию в тепло, которое увеличивает внутреннюю энергию шайбы и поверхности льда. Поскольку тепло быстро рассеивается, многие ранние философы, включая Аристотеля , ошибочно заключили, что движущиеся объекты останавливаются спонтанно. [ требуется цитата ]
Когда объект толкают вдоль поверхности по пути C, энергия, преобразованная в тепло, определяется линейным интегралом в соответствии с определением работы.
где
- это сила трения,
- — вектор, полученный путем умножения величины нормальной силы на единичный вектор, направленный против движения объекта,
- - коэффициент трения, который находится внутри интеграла, поскольку он может меняться от места к месту (например, если материал изменяется вдоль пути),
- это положение объекта.
Рассеивание энергии за счет трения в процессе является классическим примером термодинамической необратимости . [31]
Работа трения
Работа, выполняемая трением, может привести к деформации, износу и нагреву, которые могут повлиять на свойства контактной поверхности (даже на коэффициент трения между поверхностями). Это может быть полезным, как при полировке . Работа трения используется для смешивания и соединения материалов, например, в процессе сварки трением . Чрезмерная эрозия или износ сопряженных скользящих поверхностей происходит, когда работа, вызванная силами трения, достигает неприемлемого уровня. Более твердые частицы коррозии, попавшие между сопряженными поверхностями в относительном движении ( фреттинг ), усиливают износ сил трения. Поскольку поверхности изнашиваются работой, вызванной трением, посадка и отделка поверхности объекта могут ухудшаться до тех пор, пока он не перестанет функционировать должным образом. [78] Например, заклинивание или выход из строя подшипника могут возникнуть в результате чрезмерного износа из-за работы трения.
В системе отсчета интерфейса между двумя поверхностями статическое трение не совершает никакой работы , поскольку между поверхностями никогда не происходит смещения. В той же системе отсчета кинетическое трение всегда направлено в сторону, противоположную движению, и совершает отрицательную работу. [79] Однако в некоторых системах отсчета трение может совершать положительную работу . Это можно увидеть, поместив тяжелую коробку на ковер, а затем быстро потянув за ковер. В этом случае коробка скользит назад относительно ковра, но движется вперед относительно системы отсчета, в которой пол неподвижен. Таким образом, кинетическое трение между коробкой и ковер ускоряет коробку в том же направлении, в котором движется коробка, совершая положительную работу. [80]
Когда скольжение происходит между двумя шероховатыми телами, находящимися в контакте, алгебраическая сумма выполненных работ отлична от нуля, а алгебраическая сумма количеств тепла, полученного двумя телами, равна количеству работы, потерянной из-за трения, а общее количество полученного тепла положительно. [81] [82] В естественном термодинамическом процессе работа, выполненная агентом в окружении термодинамической системы или рабочего тела, больше работы, полученной телом, из-за трения. Термодинамическая работа измеряется изменениями переменных состояния тела, иногда называемых переменными, подобными работе, отличными от температуры и энтропии. Примерами переменных, подобных работе, которые являются обычными макроскопическими физическими переменными и которые встречаются в сопряженных парах, являются давление – объем и электрическое поле – электрическая поляризация. Температура и энтропия являются специфически термодинамически сопряженной парой переменных состояния. На них можно влиять микроскопически на атомном уровне с помощью таких механизмов, как трение, теплопроводность и излучение. Часть работы, совершаемой агентом в окружающей среде, которая не изменяет объем рабочего тела, но рассеивается при трении, называется изохорной работой . Она воспринимается в виде тепла рабочим телом и иногда частично телом в окружающей среде. Она не учитывается как термодинамическая работа, получаемая рабочим телом.
Приложения
Трение является важным фактором во многих инженерных дисциплинах.
Транспорт
- Автомобильные тормоза по своей сути полагаются на трение, замедляя транспортное средство путем преобразования его кинетической энергии в тепло. Кстати, безопасное рассеивание этого большого количества тепла является одной из технических проблем при проектировании тормозных систем. Дисковые тормоза полагаются на трение между диском и тормозными колодками , которые сжимаются поперечно вращающемуся диску. В барабанных тормозах тормозные колодки или колодки прижимаются наружу к вращающемуся цилиндру (тормозному барабану) для создания трения. Поскольку тормозные диски могут охлаждаться более эффективно, чем барабаны, дисковые тормоза имеют лучшую тормозную способность. [83]
- Сцепление с рельсами относится к сцеплению колес поезда с рельсами, см. Механика фрикционного контакта .
- Скользкость дороги является важным фактором конструкции и безопасности автомобилей [84]
- Расщепленное трение — особенно опасное состояние, возникающее из-за различного трения по обе стороны автомобиля.
- Текстура дороги влияет на взаимодействие шин и дорожного покрытия.
Измерение
- Трибометр — это прибор, измеряющий трение на поверхности.
- Профилограф — это прибор, используемый для измерения шероховатости поверхности дорожного покрытия .
Использование в быту
- Трение используется для нагрева и воспламенения спичек (трение между головкой спички и трущейся поверхностью спичечного коробка). [85]
- Липкие подушечки используются для предотвращения соскальзывания предметов с гладких поверхностей за счет эффективного увеличения коэффициента трения между поверхностью и предметом.
Смотрите также
Ссылки
- ^ abc Hanaor, D.; Gan, Y.; Einav, I. (2016). «Статическое трение на фрактальных интерфейсах». Tribology International . 93 : 229–238. arXiv : 2106.01473 . doi : 10.1016/j.triboint.2015.09.016. S2CID 51900923.
- ^ ab "трение". Словарь Merriam-Webster.com . Merriam-Webster.
- ^ ab "Трение | Определение, типы и формула | Britannica". www.britannica.com . 2024-09-11. Архивировано из оригинала 2024-09-16 . Получено 2024-10-07 .
- ^ ab Ghose, Tia; опубликовано, Ailsa Harvey (2022-02-08). "Что такое трение?". livescience.com . Архивировано из оригинала 2024-05-20 . Получено 07.10.2024 .
- ^ Митчелл, Люк (ноябрь 2012 г.). Уорд, Джейкоб (ред.). «Вымысел нетрения». Popular Science . № 5. 281 (ноябрь 2012 г.): 40.
- ^ Ghose, Tia; опубликовано, Ailsa Harvey (2022-02-08). "Что такое трение?". livescience.com . Архивировано из оригинала 2024-05-20 . Получено 07.10.2024 .
- ^ ab Beer, Ferdinand P. ; Johnston, E. Russel Jr. (1996). Векторная механика для инженеров (шестое изд.). McGraw-Hill. стр. 397. ISBN 978-0-07-297688-5.
- ^ ab Meriam, JL; Kraige, LG (2002). Инженерная механика (пятое изд.). John Wiley & Sons. стр. 328. ISBN 978-0-471-60293-4.
- ^ Руина, Энди; Пратап, Рудра (2002). Введение в статику и динамику (PDF) . Oxford University Press. стр. 713. Архивировано (PDF) из оригинала 2019-05-25 . Получено 2008-12-20 .
- ^ Хиббелер, RC (2007). Инженерная механика (Одиннадцатое изд.). Pearson, Prentice Hall. стр. 393. ISBN 978-0-13-127146-3.
- ^ Soutas-Little, Robert W.; Inman, Balint (2008). Инженерная механика . Томсон. стр. 329. ISBN 978-0-495-29610-2.
- ^ ab Chatterjee, Sudipta (2008). Трибологические свойства псевдоупругого никель-титана (диссертация). Калифорнийский университет. стр. 11–12. ISBN 978-0-549-84437-2– через ProQuest.
Классические греческие философы, такие как Аристотель, Плиний Старший и Витрувий, писали о существовании трения, влиянии смазочных материалов и преимуществах металлических подшипников около 350 г. до н.э.
[ постоянная мертвая ссылка ] - ^ Фишбейн, Пол М.; Гасиорович, Стивен; Торнтон, Стивен Т. (1993). Физика для ученых и инженеров . Том I (Расширенное издание). Энглвуд Клиффс, Нью-Джерси: Prentice Hall. стр. 135. ISBN 978-0-13-663246-7.
Фемистий впервые заявил около 350 г. до н. э. [ так в оригинале ] , что трение движения слабее максимального значения трения покоя.
- ^ Хехт, Юджин (2003). Физика: Алгебра/Триг (3-е изд.). Cengage Learning. ISBN 978-0-534-37729-8.
- ^ Самбурский, Сэмюэл (2014). Физический мир поздней античности. Princeton University Press. С. 65–66. ISBN 978-1-4008-5898-9. Архивировано из оригинала 2024-10-07 . Получено 2016-11-01 .
- ^ abcde Доусон, Дункан (1997). История трибологии (2-е изд.). Профессиональное инженерное издательство. ISBN 978-1-86058-070-3.
- ^ abc Armstrong-Hélouvry, Brian (1991). Управление машинами с трением. США: Springer. С. 10. ISBN 978-0-7923-9133-3. Архивировано из оригинала 2024-10-07 . Получено 2020-06-07 .
- ^ ab van Beek, Anton. "История трения в науке". tribology-abc.com. Архивировано из оригинала 2011-08-07 . Получено 2011-03-24 .
- ^ Хатчингс, Ян М. (2016). «Исследования трения Леонардо да Винчи» (PDF) . Износ . 360–361: 51–66. doi :10.1016/j.wear.2016.04.019. Архивировано (PDF) из оригинала 2016-08-03.
- ^ Хатчингс, Ян М. (2016-08-15). «Исследования трения Леонардо да Винчи». Wear . 360–361: 51–66. doi :10.1016/j.wear.2016.04.019. Архивировано из оригинала 2021-09-18 . Получено 2019-07-09 .
- ^ Кирк, Том (22 июля 2016 г.). «Исследование показывает, что «неуместные» каракули Леонардо да Винчи отмечают место, где он впервые записал законы трения». phys.org . Архивировано из оригинала 25-07-2016 . Получено 26-07-2016 .
- ^ ab Попова, Елена; Попов, Валентин Л. (2015-06-01). "Исследования работ Кулона и Амонтона и обобщенные законы трения". Трение . 3 (2): 183–190. doi : 10.1007/s40544-015-0074-6 .
- ^ Форест де Белидор, Бернар . "Richtige Grund-Sätze der Friction-Berechnung. Архивировано 27 апреля 2021 г. в Wayback Machine " ("Правильные основы расчета трения"), 1737 г. (на немецком языке )
- ^ "Leonhard Euler". Friction Module . Nano World. 2002. Архивировано из оригинала 2011-05-07 . Получено 2011-03-25 .
- ^ Goedecke, Andreas (2014). Переходные эффекты при трении: ползучесть фрактальной неровности. Springer Science and Business Media. стр. 3. ISBN 978-3-7091-1506-0. Архивировано из оригинала 2024-10-07 . Получено 2020-11-11 .
- ↑ Бенджамин Томпсон (1798). «Исследование относительно источника тепла, возбуждаемого трением», Архивировано 07.10.2024 в Wayback Machine Philosophical Transactions of the Royal Society of London , 88 : 80–102. doi :10.1098/rstl.1798.0006
- ^ Бланделл, С. Дж., Бланделл, К. М. (2006). Концепции в тепловой физике , Oxford University Press, Оксфорд, Великобритания, ISBN 978-0-19-856769-1 , стр. 106.
- ^ Джоуль, Дж. П. (1845). «О механическом эквиваленте тепла». Философские труды Лондонского королевского общества . 140 : 61–82. 1850. doi : 10.1098/rstl.1850.0004 .
- ^ Флиминг Дженкин и Джеймс Альфред Юинг (1877) «О трении между поверхностями, движущимися на малых скоростях». Архивировано 18 сентября 2021 г. в Wayback Machine , Philosophical Magazine Series 5, том 4, стр. 308–10; ссылка из Библиотеки наследия биоразнообразия
- ^ Брайан, Джордж Хартли (1907). «Термодинамика, вводный трактат, посвященный главным образом первым принципам и их прямым приложениям». Лейпциг, Тойбнер . Получено 23 июня 2023 г.
- ^ аб Планк, М. (1926). «Über die Begründung des zweiten Hauptsatzes der Thermodynamik», Sitzungsber. Пройсс. Акад. Висс., Физ. Математика. кл. , 453—463.
- ^ Air Brake Association (1921). Принципы и конструкция фундаментной тормозной оснастки. Air brake association. стр. 5. Архивировано из оригинала 2024-10-07 . Получено 2017-07-27 .
- ^ Валентин Л. Попов (17 января 2014 г.). «Обобщенный закон трения между эластомерами и шероховатыми телами различной формы». Sci. Rep . 4 : 3750. Bibcode :2014NatSR...4E3750P. doi :10.1038/srep03750. PMC 3894559 . PMID 24435002.
- ^ Оцуки, М.; Мацукава, Х. (2013-04-02). "Систематическое разложение закона трения Амонтона для упругого объекта, локально подчиняющегося закону Амонтона". Scientific Reports . 3 : 1586. arXiv : 1202.1716 . Bibcode : 2013NatSR...3E1586O. doi : 10.1038/srep01586. PMC 3613807 . PMID 23545778.
- ^ abcdefghijklmnopqrstu vwxyz aa ab ac ad ae af ag ah ai aj "Friction Factors – Coefficients of Friction". Архивировано из оригинала 2019-02-01 . Получено 2015-04-27 .
- ^ Феррейра, Вандерлей; Йошимура, Умберто Наоюки; Синатора, Амилтон (2012-08-30). «Сверхнизкий коэффициент трения в паре оксид алюминия–нитрид кремния, смазываемой водой». Wear . 296 (1–2): 656–659. doi :10.1016/j.wear.2012.07.030.
- ^ Tian, Y.; Bastawros, AF; Lo, CCH; Constant, AP; Russell, AM; Cook, BA (2003). "Сверхтвердые самосмазывающиеся пленки AlMgB[sub 14] для микроэлектромеханических устройств". Applied Physics Letters . 83 (14): 2781. Bibcode : 2003ApPhL..83.2781T. doi : 10.1063/1.1615677. Архивировано из оригинала 2024-10-07 . Получено 2019-01-31 .
- ^ Кляйнер, Курт (21.11.2008). «Материал, более скользкий, чем тефлон, обнаружен случайно». Архивировано из оригинала 20.12.2008 . Получено 25.12.2008 .
- ^ Хигдон, К.; Кук, Б.; Харринга, Дж.; Рассел, А.; Голдсмит, Дж.; Ку, Дж.; Блау, П. (2011). «Механизмы трения и износа в нанопокрытиях AlMgB14-TiB2». Wear . 271 (9–10): 2111–2115. doi :10.1016/j.wear.2010.11.044.
- ^ abcde Коэффициент трения Архивировано 8 марта 2009 г. на Wayback Machine . EngineersHandbook.com
- ^ abcdefghijklmnopq Барретт, Ричард Т. (1 марта 1990 г.). "(NASA-RP-1228) Руководство по проектированию креплений". Сервер технических отчетов NASA . Исследовательский центр NASA Lewis: 16. hdl :2060/19900009424. Архивировано из оригинала 7 октября 2024 г. Получено 3 августа 2020 г.
- ^ ab "Коэффициенты трения человеческих суставов". Архивировано из оригинала 2024-10-07 . Получено 2015-04-27 .
- ^ abcdefghi "Инструментальный набор: трение и коэффициенты трения". Архивировано из оригинала 2013-12-03 . Получено 2008-11-23 .
- ^ Динвибель, Мартин и др. (2004). "Сверхсмазочная способность графита" (PDF) . Phys. Rev. Lett . 92 (12): 126101. Bibcode :2004PhRvL..92l6101D. doi :10.1103/PhysRevLett.92.126101. PMID 15089689. S2CID 26811802. Архивировано (PDF) из оригинала 2011-09-17 . Получено 2011-09-01 .
- ^ многомасштабные истоки статического трения Архивировано 2021-09-18 на Wayback Machine 2016
- ^ Гринвуд JA и Дж. Б. Уильямсон (1966). «Контакт номинально плоских поверхностей». Труды Лондонского королевского общества A: Математические, физические и инженерные науки . 295 (1442).
- ^ Накано, К.; Попов, В.Л. (2020-12-10). "Динамическое сцепление без статического трения: роль вращения вектора трения". Physical Review E. 102 ( 6): 063001. Bibcode : 2020PhRvE.102f3001N. doi : 10.1103/PhysRevE.102.063001. hdl : 10131/00013921 . PMID 33466084. S2CID 230599544.
- ^ Бхавикатти, СС; К.Г. Раджашекараппа (1994). Инженерная механика. Нью Эйдж Интернэшнл. п. 112. ИСБН 978-81-224-0617-7. Архивировано из оригинала 2024-10-07 . Получено 2007-10-21 .
- ^ Шеппард, Шери ; Тонг, Бенсон Х.; Анагнос, Талия (2005). Статика: Анализ и проектирование систем в равновесии . Wiley and Sons. стр. 618. ISBN 978-0-471-37299-8.
В общем случае для данных контактирующих поверхностей μ k < μ s
- ^ Мериам, Джеймс Л.; Крейг, Л. Гленн; Палм, Уильям Джон (2002). Инженерная механика: Статика . Wiley and Sons. стр. 330. ISBN 978-0-471-40646-4Кинетическая
сила трения обычно несколько меньше максимальной силы трения покоя.
- ^ Фейнман, Ричард П.; Лейтон, Роберт Б.; Сэндс, Мэтью (1964). «Лекции Фейнмана по физике, т. I, стр. 12–5». Эддисон-Уэсли. Архивировано из оригинала 10.03.2021 . Получено 16.10.2009 .
- ^ ab Persson, BN; Volokitin, A. I (2002). "Теория трения резины: Нестационарное скольжение" (PDF) . Physical Review B . 65 (13): 134106. Bibcode :2002PhRvB..65m4106P. doi :10.1103/PhysRevB.65.134106. Архивировано (PDF) из оригинала 2021-09-18 . Получено 2019-01-31 .
- ^ Перссон, Б. Н. Дж. (2000). Трение скольжения: физические принципы и приложения. Springer. ISBN 978-3-540-67192-3. Архивировано из оригинала 2024-10-07 . Получено 2016-01-23 .
- ^ Макконен, Л. (2012). «Термодинамическая модель трения скольжения». AIP Advances . 2 (1): 012179. Bibcode : 2012AIPA....2a2179M. doi : 10.1063/1.3699027 .
- ^ Николс, Эдвард Лимингтон; Франклин, Уильям Саддардс (1898). Элементы физики. Т. 1. Macmillan. стр. 101. Архивировано из оригинала 2024-10-07 . Получено 2020-06-07 .
- ^ Тернес, Маркус; Лутц, Кристофер П.; Хирджибехедин, Сайрус Ф.; Гиссибл, Франц Дж.; Хайнрих, Андреас Дж. (2008-02-22). «Сила, необходимая для перемещения атома на поверхности» (PDF) . Science . 319 (5866): 1066–1069. Bibcode :2008Sci...319.1066T. doi :10.1126/science.1150288. PMID 18292336. S2CID 451375. Архивировано (PDF) из оригинала 20 июля 2018 г.
- ^ ab Deng, Zhao; et al. (14 октября 2012 г.). «Зависящий от адгезии отрицательный коэффициент трения химически модифицированного графита в наномасштабе». Nature . 11 (12): 1032–7. Bibcode :2012NatMa..11.1032D. doi :10.1038/nmat3452. PMID 23064494.
- «В наномасштабе графит может перевернуть трение с ног на голову». Журнал R&D . 2012-10-17. Архивировано из оригинала 2013-07-31.
- ^ Haslinger, J.; Nedlec, JC (1983). «Аппроксимация задачи Синьорини с трением, подчиняющимся закону Кулона» (PDF) . Математические методы в прикладных науках . 5 (1): 422–437. Bibcode :1983MMAS....5..422H. doi :10.1002/mma.1670050127. hdl :10338.dmlcz/104086. Архивировано (PDF) из оригинала 2024-10-07 . Получено 2019-09-19 .
- ^ Alart, P.; Curnier, A. (1991). "Смешанная формулировка для задач фрикционного контакта, склонных к методу решения, подобному методу Ньютона" (PDF) . Computer Methods in Applied Mechanics and Engineering . 92 (3): 353–375. Bibcode :1991CMAME..92..353A. doi :10.1016/0045-7825(91)90022-X. Архивировано (PDF) из оригинала 2024-10-07 . Получено 2024-03-29 .
- ^ Acary, V.; Cadoux, F.; Lemaréchal, C.; Malick, J. (2011). «Формулировка линейной дискретной задачи трения Кулона с помощью выпуклой оптимизации». Журнал прикладной математики и механики . 91 (2): 155–175. Bibcode :2011ZaMM...91..155A. doi :10.1002/zamm.201000073. S2CID 17280625. Архивировано из оригинала 2024-10-07 . Получено 2018-04-20 .
- ^ De Saxcé, G.; Feng, Z.-Q. (1998). «Бипотенциальный метод: конструктивный подход к разработке полного закона контакта с трением и улучшенными численными алгоритмами». Математическое и компьютерное моделирование . 28 (4): 225–245. doi : 10.1016/S0895-7177(98)00119-8 .
- ^ Simo, JC; Laursen, TA (1992). «Расширенная лагранжева обработка контактных задач, включающих трение». Компьютеры и структуры . 42 (2): 97–116. doi : 10.1016/0045-7949(92)90540-G .
- ^ Acary, V.; Brogliato, B. (2008). Численные методы для негладких динамических систем. Приложения в механике и электронике . Том 35. Springer Verlag Heidelberg .
- ^ Бигони, Д. (2012-07-30). Нелинейная механика твердого тела: теория бифуркации и неустойчивость материала . Cambridge University Press, 2012. ISBN 978-1-107-02541-7.
- ^ Адамс, ГГ (1995). «Самовозбуждающиеся колебания двух упругих полупространств, скользящих с постоянным коэффициентом трения». Журнал прикладной механики . 62 (4): 867–872. Bibcode : 1995JAM....62..867A. doi : 10.1115/1.2896013.
- ^ Мартинс, JA, Фариа, LO и Гимарайнш, J. (1995). «Динамические поверхностные решения в линейной упругости и вязкоупругости с граничными условиями трения». Журнал вибрации и акустики . 117 (4): 445–451. doi :10.1115/1.2874477.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ^ M, Nosonovsky; G., Adams G. (2004). «Вибрация и устойчивость фрикционного скольжения двух упругих тел с волнистым контактным интерфейсом». Журнал прикладной механики . 71 (2): 154–161. Bibcode : 2004JAM....71..154N. doi : 10.1115/1.1653684.
- ^ J., Flint; J., Hultén (2002). «Модальная связь, вызванная деформацией накладки, как генератор визга в модели дискового тормоза с распределенными параметрами». Журнал звука и вибрации . 254 (1): 1–21. Bibcode : 2002JSV...254....1F. doi : 10.1006/jsvi.2001.4052.
- ^ М., Крёгер; М., Нойбауэр; К., Попп (2008). «Экспериментальное исследование по предотвращению самовозбуждающихся колебаний». Phil. Trans. R. Soc. A. 366 ( 1866): 785–810. Bibcode :2008RSPTA.366..785K. doi :10.1098/rsta.2007.2127. PMID 17947204. S2CID 16395796.
- ^ R., Rice, J.; L., Ruina, A. (1983). "Stability of Steady Frictional Slipping" (PDF) . Journal of Applied Mechanics . 50 (2): 343–349. Bibcode :1983JAM....50..343R. CiteSeerX 10.1.1.161.5207 . doi :10.1115/1.3167042. Архивировано (PDF) из оригинала 2010-06-22.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ^ Bigoni, D.; Noselli, G. (2011). «Экспериментальные доказательства неустойчивости флаттера и дивергенции, вызванной сухим трением». Журнал механики и физики твердого тела . 59 (10): 2208–2226. Bibcode :2011JMPSo..59.2208B. CiteSeerX 10.1.1.700.5291 . doi :10.1016/j.jmps.2011.05.007. Архивировано из оригинала 2020-08-18 . Получено 2011-11-30 .
- ^ Носоновский, Майкл (2013). Фрикционно-индуцированные колебания и самоорганизация: механика и неравновесная термодинамика скользящего контакта. CRC Press. стр. 333. ISBN 978-1-4665-0401-1.
- ^ Эйнштейн, А. (1909). О развитии наших взглядов на природу и состав излучения. Переведено в: The Collected Papers of Albert Einstein, т. 2 (Princeton University Press, Princeton, 1989) . Princeton, NJ: Princeton University Press. стр. 391.
- ^ Силлиман, Бенджамин (1871) Принципы физики, или натуральной философии , Айвисон, Блейкман, Тейлор и издатели компании
- ^ Батт, Ханс-Юрген; Граф, Карлхайнц и Каппль, Майкл (2006) Физика и химия интерфейсов , Wiley, ISBN 3-527-40413-9
- ^ Хоган, К. Майкл (1973). «Анализ шума на шоссе». Загрязнение воды, воздуха и почвы . 2 (3): 387–392. Bibcode : 1973WASP....2..387H. doi : 10.1007/BF00159677. S2CID 109914430.
- ^ Валентин Л. Попов; Ларс Фолль; Стефан Куше; Цян Ли; Светлана В. Рожкова (2018). «Обобщенная процедура основной кривой для трения эластомера с учетом зависимостей от скорости, температуры и нормальной силы». Tribology International . 120 : 376–380. arXiv : 1604.03407 . doi : 10.1016/j.triboint.2017.12.047. S2CID 119288819.
- ^ Байер, Рэймонд Джордж (2004). Механический износ. CRC Press. С. 1, 2. ISBN 978-0-8247-4620-9. Архивировано из оригинала 2024-10-07 . Получено 2008-07-07 .
- ^ Ден Хартог, JP (1961). Механика. Публикации Courier Dover. п. 142. ИСБН 978-0-486-60754-2. Архивировано из оригинала 2024-10-07 . Получено 2020-06-07 .
- ^ Леонард, Уильям Дж. (2000). Minds-on Physics. Кендалл/Хант. стр. 603. ISBN 978-0-7872-3932-9. Архивировано из оригинала 2024-10-07 . Получено 2020-06-07 .
- ^ Брайан, Джордж Хартли (1907). «Термодинамика, вводный трактат, посвященный главным образом первым принципам и их прямым приложениям». Лейпциг, Тойбнер. стр. 48–49 . Получено 23 июня 2023 г.
 В данной статье использован текст из этого источника, находящегося в общественном достоянии .
В данной статье использован текст из этого источника, находящегося в общественном достоянии . - ↑ Бриджмен, П. У., 1943, Природа термодинамики , Издательство Гарвардского университета, стр. 47–56.
- ^ "How Do Car Brakes Work?". Wonderopolis. Архивировано из оригинала 7 октября 2024 г. Получено 4 ноября 2018 г.
- ^ Искандер, Р.; Стивенс, А. "Эффективность применения высокофрикционного покрытия - снижение аварий.pdf" (PDF) . Архивировано (PDF) из оригинала 2017-09-03 . Получено 2017-09-03 .
- ^ "Как работает зажигание спички?". curious.com . Curiosity. 11 ноября 2015 г. Архивировано из оригинала 5 ноября 2018 г. Получено 4 ноября 2018 г.
Внешние ссылки
- . Энциклопедия Британника . Т. 11 (11-е изд.). 1911.
- Коэффициенты трения – таблицы коэффициентов, а также множество ссылок
- Измерение силы трения
- Physclips: Механика с анимациями и видеоклипами от Университета Нового Южного Уэльса
- Значения коэффициента трения – Справочник CRC по химии и физике
- Коэффициенты трения различных пар материалов в атмосфере и вакууме.



































