Колоколообразная функция

Для проверки этой статьи нужны дополнительные цитаты . Помогите улучшить эту статью , добавив ссылки на надежные источники . Неподтвержденный материал может быть оспорен и удален. Найти источники:  "Bell-shaped function" – новости  · газеты  · книги  · ученый  · JSTOR ( декабрь 2018 г. ) ( Узнайте, как и когда удалять это сообщение )

Колоколообразная функция или просто «колоколообразная кривая» — это математическая функция, имеющая характерную « колоколообразную » кривую. Эти функции обычно непрерывны или гладки, асимптотически стремятся к нулю при больших отрицательных/положительных x и имеют один унимодальный максимум при малых x. Следовательно, интеграл колоколообразной функции обычно является сигмоидной функцией . Колоколообразные функции также обычно симметричны.

Многие распространённые функции распределения вероятностей представляют собой колоколообразные кривые.

Некоторые колоколообразные функции, такие как функция Гаусса и распределение вероятностей распределения Коши , могут быть использованы для построения последовательностей функций с убывающей дисперсией , которые приближаются к дельта-распределению Дирака . ^[1] Действительно, дельта-распределение Дирака можно грубо представить как колоколообразную кривую с дисперсией, стремящейся к нулю.

Вот некоторые примеры:

• Гауссова функция , функция плотности вероятности нормального распределения . Это архетипическая колоколообразная функция, часто встречающаяся в природе как следствие центральной предельной теоремы .

${\displaystyle f(x)=ae^{-(x-b)^{2}/(2c^{2})}}$

• Обобщенная колоколообразная функция принадлежности нечеткой логики ^{[2] [3]}

${\displaystyle f(x)={\frac {1}{1+\left|{\frac {x-c}{a}}\right|^{2b}}}}$

• Гиперболический секанс . Это также производная функции Гудермана .

${\displaystyle f(x)=\operatorname {sech} (x)={\frac {2}{e^{x}+e^{-x}}}}$

• Ведьма Агнеси , функция плотности вероятности распределения Коши . Это также масштабированная версия производной функции арктангенса .

${\displaystyle f(x)={\frac {8a^{3}}{x^{2}+4a^{2}}}}$

• Функция удара

${\displaystyle \varphi _{b}(x)={\begin{cases}\exp {\frac {b^{2}}{x^{2}-b^{2}}}&|x|<b,\\0&|x|\geq b.\end{cases}}}$

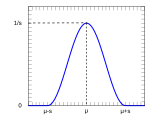
• Тип приподнятых косинусов, например, распределение приподнятых косинусов или фильтр приподнятых косинусов

${\displaystyle f(x;\mu ,s)={\begin{cases}{\frac {1}{2s}}\left[1+\cos \left({\frac {x-\mu }{s}}\pi \right)\right]&{\text{for }}\mu -s\leq x\leq \mu +s,\\[3pt]0&{\text{otherwise.}}\end{cases}}}$

• Большинство оконных функций похожи на окна Кайзера.

• Производная логистической функции . Это масштабированная версия производной функции гиперболического тангенса .

${\displaystyle f(x)={\frac {e^{x}}{\left(1+e^{x}\right)^{2}}}}$

• Некоторые алгебраические функции . Например

${\displaystyle f(x)={\frac {1}{(1+x^{2})^{3/2}}}}$

• 
  sech( x ) (синим цветом)
• 
  Ведьма Агнеси
• 
  φ _b для b = 1
• 
  Приподнятый косинус PDF
• 
  Окно Кайзера