Функция удара

В математике функция выпуклости (также называемая тестовой функцией ) — это функция на евклидовом пространстве , которая является как гладкой (в смысле наличия непрерывных производных всех порядков), так и компактной с носителем . Множество всех функций выпуклости с областью определения образует векторное пространство , обозначаемое или Двойственное пространство этого пространства, наделенное подходящей топологией, является пространством распределений .${\displaystyle f:\mathbb {R} ^{n}\to \mathbb {R} }$ ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle \mathbb {R} ^{n}}$${\displaystyle \mathrm {C} _{0}^{\infty }(\mathbb {R} ^{n})}$${\ displaystyle \ mathrm {C} _ {\ mathrm {c} } ^ {\ infty } (\ mathbb {R} ^ {n}).}$

Функция, заданная как, является примером функции выпуклости в одном измерении. Из построения ясно, что эта функция имеет компактный носитель, поскольку функция действительной линии имеет компактный носитель тогда и только тогда, когда она имеет ограниченный замкнутый носитель. Доказательство гладкости следует тем же принципам, что и для связанной функции, обсуждаемой в статье Неаналитическая гладкая функция . Эту функцию можно интерпретировать как гауссову функцию, масштабированную для вписывания в единичный круг: подстановка соответствует отправке в${\displaystyle \Psi :\mathbb {R} \to \mathbb {R} }$$${\displaystyle \Psi (x)={\begin{cases}\exp \left(-{\frac {1}{1-x^{2}}}\right),&{\text{ if }}|x|<1,\\0,&{\text{ if }}|x|\geq 1,\end{cases}}}$$ ${\displaystyle \exp \left(-y^{2}\right)}$${\displaystyle y^{2}={1}/{\left(1-x^{2}\right)}}$${\displaystyle x=\pm 1}$${\displaystyle y=\infty .}$

Простой пример (квадратной) функции выпуклости в переменных получается путем взятия произведения копий указанной выше функции выпуклости в одной переменной, то есть ${\displaystyle n}$${\displaystyle n}$$${\displaystyle \Phi (x_{1},x_{2},\dots ,x_{n})=\Psi (x_{1})\Psi (x_{2})\cdots \Psi (x_{n}).}$$

Радиально-симметричная функция выпуклости в переменных может быть сформирована путем взятия функции, определяемой . Эта функция поддерживается на единичном шаре с центром в начале координат.${\displaystyle n}$${\displaystyle \Psi _{n}:\mathbb {R} ^{n}\to \mathbb {R} }$${\displaystyle \Psi _{n}(\mathbf {x} )=\Psi (|\mathbf {x} |)}$

В качестве другого примера возьмем , который положителен в одном месте и равен нулю в других местах, например ${\displaystyle h}$${\displaystyle (c,d)}$

${\displaystyle h(x)={\begin{cases}\exp \left(-{\frac {1}{(x-c)(d-x)}}\right),&c<x<d\\0,&\mathrm {otherwise} \end{cases}}}$.

Функции плавного перехода

Рассмотрим функцию

${\displaystyle f(x)={\begin{cases}e^{-{\frac {1}{x}}}&{\text{if }}x>0,\\0&{\text{if }}x\leq 0,\end{cases}}}$

определено для каждого действительного числа x .

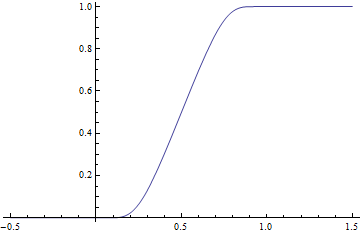
Функция

${\displaystyle g(x)={\frac {f(x)}{f(x)+f(1-x)}},\qquad x\in \mathbb {R} ,}$

имеет строго положительный знаменатель всюду на действительной прямой, поэтому g также является гладкой. Кроме того, g ( x ) = 0 для x  ≤ 0 и g ( x ) = 1 для x  ≥ 1, поэтому она обеспечивает плавный переход от уровня 0 к уровню 1 в единичном интервале [0, 1]. Чтобы иметь плавный переход в действительном интервале [ a , b ] с a  <  b , рассмотрим функцию

${\displaystyle \mathbb {R} \ni x\mapsto g{\Bigl (}{\frac {x-a}{b-a}}{\Bigr )}.}$

Для действительных чисел a < b < c < d гладкая функция

${\displaystyle \mathbb {R} \ni x\mapsto g{\Bigl (}{\frac {x-a}{b-a}}{\Bigr )}\,g{\Bigl (}{\frac {d-x}{d-c}}{\Bigr )}}$

равна 1 на замкнутом интервале [ b , c ] и исчезает за пределами открытого интервала ( a , d ), поэтому она может служить функцией выпуклости.

Необходимо соблюдать осторожность, поскольку, например, принятие , приводит к:${\displaystyle \{a=-1\}<\{b=c=0\}<\{d=1\}}$

${\displaystyle q(x)={\frac {1}{1+e^{\frac {1-2|x|}{x^{2}-|x|}}}}}$

которая не является бесконечно дифференцируемой функцией (и, следовательно, не является «гладкой»), поэтому ограничения a < b < c < d должны строго выполняться.

Некоторые интересные факты о функции:

${\displaystyle q(x,a)={\frac {1}{1+e^{\frac {a(1-2|x|)}{x^{2}-|x|}}}}}$

Это те, которые создают плавные переходные кривые с «почти» постоянными наклонными краями (функция рельефа с истинно прямыми наклонами изображена в этом другом примере ).${\displaystyle q\left(x,{\frac {\sqrt {3}}{2}}\right)}$

Правильным примером функции плавного рельефа будет:

${\displaystyle u(x)={\begin{cases}1,{\text{if }}x=0,\\0,{\text{if }}|x|\geq 1,\\{\frac {1}{1+e^{\frac {1-2|x|}{x^{2}-|x|}}}},{\text{otherwise}},\end{cases}}}$

Правильным примером функции плавного перехода будет:

${\displaystyle w(x)={\begin{cases}{\frac {1}{1+e^{\frac {2x-1}{x^{2}-x}}}}&{\text{if }}0<x<1,\\0&{\text{if }}x\leq 0,\\1&{\text{if }}x\geq 1,\end{cases}}}$

где можно заметить, что его можно представить также через гиперболические функции :

${\displaystyle {\frac {1}{1+e^{\frac {2x-1}{x^{2}-x}}}}={\frac {1}{2}}\left(1-\tanh \left({\frac {2x-1}{2(x^{2}-x)}}\right)\right)}$

Можно построить функции выпуклости «по спецификациям». Формально, если — произвольное компактное множество в измерениях и — открытое множество , содержащее , то существует функция выпуклости , которая находится на и вне Поскольку можно взять очень малую окрестность , это равносильно возможности построить функцию, которая находится на и быстро спадает вне , оставаясь при этом гладкой.${\displaystyle K}$${\displaystyle n}$${\displaystyle U}$${\displaystyle K,}$${\displaystyle \phi }$${\displaystyle 1}$${\displaystyle K}$${\displaystyle 0}$${\displaystyle U.}$${\displaystyle U}$${\displaystyle K,}$${\displaystyle 1}$${\displaystyle K}$${\displaystyle 0}$${\displaystyle K,}$

Функции Bump, определенные в терминах свертки

Построение происходит следующим образом. Рассматривается компактная окрестность , содержащаяся в так Характеристическая функция будет равна на и вне так в частности, она будет равна на и вне Однако эта функция не является гладкой. Основная идея состоит в том, чтобы немного сгладить, взяв свертку с смягчителем . Последний представляет собой просто функцию выпуклости с очень малым носителем, интеграл которой равен Такой смягчитель можно получить, например, взяв функцию выпуклости из предыдущего раздела и выполнив соответствующие масштабирования.${\displaystyle V}$${\displaystyle K}$${\displaystyle U,}$${\displaystyle K\subseteq V^{\circ }\subseteq V\subseteq U.}$ ${\displaystyle \chi _{V}}$${\displaystyle V}$${\displaystyle 1}$${\displaystyle V}$${\displaystyle 0}$${\displaystyle V,}$${\displaystyle 1}$${\displaystyle K}$${\displaystyle 0}$${\displaystyle U.}$${\displaystyle \chi _{V}}$${\displaystyle \chi _{V}}$${\displaystyle 1.}$${\displaystyle \Phi }$

Функции Bump, определенные в терминах функции с поддержкой${\displaystyle c:\mathbb {R} \to [0,\infty )}$${\displaystyle (-\infty ,0]}$

Альтернативная конструкция, которая не включает свертку, теперь подробно описана. Она начинается с построения гладкой функции , которая положительна на заданном открытом подмножестве и исчезает вне ^[1] Носитель этой функции равен замыканию в , поэтому если является компактным, то является функцией выпуклости. ${\displaystyle f:\mathbb {R} ^{n}\to \mathbb {R} }$${\displaystyle U\subseteq \mathbb {R} ^{n}}$${\displaystyle U.}$${\displaystyle {\overline {U}}}$${\displaystyle U}$${\displaystyle \mathbb {R} ^{n},}$${\displaystyle {\overline {U}}}$${\displaystyle f}$

Начнем с любой гладкой функции , которая обращается в нуль на отрицательных действительных числах и положительна на положительных действительных числах (то есть, и далее , где непрерывность слева требует ); примером такой функции является для и в противном случае. ^[1] Зафиксируем открытое подмножество и обозначим обычную евклидову норму через (так что наделено обычной евклидовой метрикой ). Следующая конструкция определяет гладкую функцию , которая положительна на и обращается в нуль вне ^[1] Так, в частности, если является относительно компактным, то эта функция будет функцией выпуклости.${\displaystyle c:\mathbb {R} \to \mathbb {R} }$${\displaystyle c=0}$${\displaystyle (-\infty ,0)}$${\displaystyle c>0}$${\displaystyle (0,\infty ),}$${\displaystyle c(0)=0}$${\displaystyle c(x):=e^{-1/x}}$${\displaystyle x>0}$${\displaystyle c(x):=0}$${\displaystyle U}$${\displaystyle \mathbb {R} ^{n}}$${\displaystyle \|\cdot \|}$${\displaystyle \mathbb {R} ^{n}}$${\displaystyle f:\mathbb {R} ^{n}\to \mathbb {R} }$${\displaystyle U}$${\displaystyle U.}$${\displaystyle U}$${\displaystyle f}$

Если то пусть , а если то пусть ; так что предположим, что не является ни одним из этих. Пусть будет открытым покрытием из открытых шаров, где открытый шар имеет радиус и центр Тогда отображение, определяемое как является гладкой функцией, которая положительна на и исчезает вне ^[1] Для каждого пусть , где этот супремум не равен (так что является неотрицательным действительным числом), потому что все частные производные исчезают (равенны ) в любой точке вне , тогда как на компактном множестве значения каждой из (конечного числа) частных производных (равномерно) ограничены сверху некоторым неотрицательным действительным числом. ^{[примечание 1]} Ряд равномерно сходится на к гладкой функции , которая положительна на и исчезает вне ^[1] Более того, для любых неотрицательных целых чисел ^[1] где этот ряд также равномерно сходится на (потому что всякий раз, когда то абсолютное значение ^-го члена равно ). Это завершает построение. ${\displaystyle U=\mathbb {R} ^{n}}$${\displaystyle f=1}$${\displaystyle U=\varnothing }$${\displaystyle f=0}$${\displaystyle U}$${\displaystyle \left(U_{k}\right)_{k=1}^{\infty }}$${\displaystyle U}$${\displaystyle U_{k}}$${\displaystyle r_{k}>0}$${\displaystyle a_{k}\in U.}$${\displaystyle f_{k}:\mathbb {R} ^{n}\to \mathbb {R} }$${\displaystyle f_{k}(x)=c\left(r_{k}^{2}-\left\|x-a_{k}\right\|^{2}\right)}$${\displaystyle U_{k}}$${\displaystyle U_{k}.}$${\displaystyle k\in \mathbb {N} ,}$$${\displaystyle M_{k}=\sup \left\{\left|{\frac {\partial ^{p}f_{k}}{\partial ^{p_{1}}x_{1}\cdots \partial ^{p_{n}}x_{n}}}(x)\right|~:~x\in \mathbb {R} ^{n}{\text{ and }}p_{1},\ldots ,p_{n}\in \mathbb {Z} {\text{ satisfy }}0\leq p_{i}\leq k{\text{ and }}p=\sum _{i}p_{i}\right\},}$$${\displaystyle +\infty }$${\displaystyle M_{k}}$${\displaystyle \left(\mathbb {R} ^{n}\setminus U_{k}\right)\cup {\overline {U_{k}}}=\mathbb {R} ^{n},}$${\displaystyle 0}$${\displaystyle x}$${\displaystyle U_{k},}$${\displaystyle {\overline {U_{k}}},}$$${\displaystyle f~:=~\sum _{k=1}^{\infty }{\frac {f_{k}}{2^{k}M_{k}}}}$$${\displaystyle \mathbb {R} ^{n}}$${\displaystyle f:\mathbb {R} ^{n}\to \mathbb {R} }$${\displaystyle U}$${\displaystyle U.}$${\displaystyle p_{1},\ldots ,p_{n}\in \mathbb {Z} ,}$$${\displaystyle {\frac {\partial ^{p_{1}+\cdots +p_{n}}}{\partial ^{p_{1}}x_{1}\cdots \partial ^{p_{n}}x_{n}}}f~=~\sum _{k=1}^{\infty }{\frac {1}{2^{k}M_{k}}}{\frac {\partial ^{p_{1}+\cdots +p_{n}}f_{k}}{\partial ^{p_{1}}x_{1}\cdots \partial ^{p_{n}}x_{n}}}}$$${\displaystyle \mathbb {R} ^{n}}$${\displaystyle k\geq p_{1}+\cdots +p_{n}}$${\displaystyle k}$${\displaystyle \leq {\tfrac {M_{k}}{2^{k}M_{k}}}={\tfrac {1}{2^{k}}}}$

Как следствие, заданные два непересекающихся замкнутых подмножества приведенной выше конструкции гарантируют существование гладких неотрицательных функций таких, что для любого тогда и только тогда, когда и аналогично, тогда и только тогда, когда то функция является гладкой и для любого тогда и только тогда, когда тогда и только тогда, когда и тогда и только тогда, когда ^[1] В частности, тогда и только тогда, когда так что если в дополнение является относительно компактным в (где подразумевает ), то будет гладкой функцией выпуклости с носителем в${\displaystyle A,B}$${\displaystyle \mathbb {R} ^{n},}$${\displaystyle f_{A},f_{B}:\mathbb {R} ^{n}\to [0,\infty )}$${\displaystyle x\in \mathbb {R} ^{n},}$ ${\displaystyle f_{A}(x)=0}$${\displaystyle x\in A,}$${\displaystyle f_{B}(x)=0}$${\displaystyle x\in B,}$$${\displaystyle h~:=~{\frac {f_{A}}{f_{A}+f_{B}}}:\mathbb {R} ^{n}\to [0,1]}$$${\displaystyle x\in \mathbb {R} ^{n},}$ ${\displaystyle h(x)=0}$${\displaystyle x\in A,}$ ${\displaystyle h(x)=1}$${\displaystyle x\in B,}$${\displaystyle 0<h(x)<1}$${\displaystyle x\not \in A\cup B.}$${\displaystyle h(x)\neq 0}$${\displaystyle x\in \mathbb {R} ^{n}\smallsetminus A,}$${\displaystyle U:=\mathbb {R} ^{n}\smallsetminus A}$${\displaystyle \mathbb {R} ^{n}}$${\displaystyle A\cap B=\varnothing }$${\displaystyle B\subseteq U}$${\displaystyle h}$${\displaystyle {\overline {U}}.}$

Хотя функции выпуклости являются гладкими, теорема о тождественности запрещает им быть аналитическими , если они не исчезают тождественно. Функции выпуклости часто используются в качестве смягчителей , как гладкие функции отсечки и для формирования гладких разбиений единицы . Они являются наиболее распространенным классом тестовых функций, используемых в анализе. Пространство функций выпуклости замкнуто относительно многих операций. Например, сумма, произведение или свертка двух функций выпуклости снова является функцией выпуклости, и любой дифференциальный оператор с гладкими коэффициентами, примененный к функции выпуклости, даст другую функцию выпуклости.

Если границы области определения функции Bump должны удовлетворять требованию «гладкости», она должна сохранять непрерывность всех своих производных, что приводит к следующему требованию на границах ее области определения:${\displaystyle \partial x,}$$${\displaystyle \lim _{x\to \partial x^{\pm }}{\frac {d^{n}}{dx^{n}}}f(x)=0,\,{\text{ for all }}n\geq 0,\,n\in \mathbb {Z} }$$

Преобразование Фурье функции выпуклости является (действительной) аналитической функцией, и ее можно распространить на всю комплексную плоскость: следовательно, она не может иметь компактный носитель, если она не равна нулю, поскольку единственная целая аналитическая функция выпуклости является нулевой функцией (см. теорему Пэли–Винера и теорему Лиувилля ). Поскольку функция выпуклости бесконечно дифференцируема, ее преобразование Фурье должно затухать быстрее, чем любая конечная степень для большой угловой частоты ^[2] Преобразование Фурье конкретной функции выпуклости сверху можно проанализировать методом седловой точки , и оно затухает асимптотически как для больших ^[3]${\displaystyle 1/k}$${\displaystyle |k|.}$$${\displaystyle \Psi (x)=e^{-1/(1-x^{2})}\mathbf {1} _{\{|x|<1\}}}$$$${\displaystyle |k|^{-3/4}e^{-{\sqrt {|k|}}}}$$${\displaystyle |k|.}$

• Функция отсечения  – Интеграционные ядра для сглаживания резких особенностейPages displaying short descriptions of redirect targets
• Лапласиан индикатора  – Предел последовательности гладких функций
• Неаналитическая гладкая функция  – Математические функции, которые являются гладкими, но не аналитическими.
• Пространство Шварца  – функциональное пространство всех функций, производные которых быстро убывают.

• Nestruev, Jet (10 сентября 2020 г.). Гладкие многообразия и наблюдаемые . Graduate Texts in Mathematics . Vol. 220. Cham, Switzerland: Springer Nature . ISBN 978-3-030-45649-8. OCLC  1195920718.