Четырехгранный купол
Эта статья в значительной степени или полностью основана на одном источнике . ( апрель 2024 г. ) |
| Четырехгранный купол | ||
|---|---|---|
 Диаграмма Шлегеля | ||
| Тип | Многогранный купол | |
| Символ Шлефли | {3,3} в рр{3,3} | |
| Клетки | 16 | 1 рр{3,3}  1+4 {3,3}  4+6 {}×{3}  |
| Лица | 42 | 24 треугольника 18 квадратов |
| Края | 42 | |
| Вершины | 16 | |
| Двойной | ||
| Группа симметрии | [3,3,1], порядок 24 | |
| Характеристики | выпуклый , с правильной поверхностью | |
В 4-мерной геометрии тетраэдрический купол представляет собой полихор, ограниченный одним тетраэдром , параллельным кубооктаэдром , соединенным 10 треугольными призмами и 4 треугольными пирамидами . [1]
Связанные многогранники
Тетраэдрический купол можно отсечь от 5-ячейки с рутинной структурой на гиперплоскости , параллельной тетраэдрической ячейке. Основание кубооктаэдра проходит через центр 5-ячейки с рутинной структурой, поэтому тетраэдрический купол содержит половину тетраэдрических и треугольных призматических ячеек 5-ячейки с рутинной структурой. Купол можно увидеть в ортогональной проекции плоскости Коксетера A 2 и A 3 5-ячейки с рутинной структурой:
| Самолет Коксетера 3 | ||
|---|---|---|
| Runcinated 5-клеточный | Тетраэдр (купольная вершина) | Кубооктаэдр (основание купола) |
 |  |  |
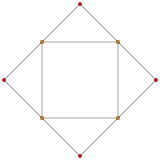| Самолет Коксетера 2 | ||
 |  |  |
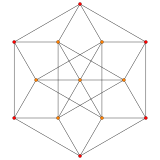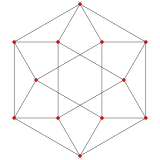Смотрите также
- Тетраэдрическая пирамида (5-ячейковая)
Ссылки
- ^ Выпуклая сегментохора Д-р Ричард Клитцинг, Симметрия: Культура и наука, т. 11, №№ 1-4, 139-181, 2000 (4,23 тетраэдр || кубооктаэдр)
Внешние ссылки
- Сегментохора: тетако, тет || со, К-4.23
 | Эта статья о 4-многограннике является заглушкой . Вы можете помочь Википедии, расширив ее. |
