Икосаэдрические соты

Икосаэдрические соты
Модель диска Пуанкаре
Тип	Гиперболические регулярные соты Однородные гиперболические соты
Символ Шлефли	{3,5,3}
Диаграмма Коксетера
Клетки	{5,3} ( правильный икосаэдр )
Лица	{3} ( треугольник )
Крайняя фигура	{3} (треугольник)
Вершинная фигура	додекаэдр
Двойной	Самодвойственный
Группа Коксетера	J 3 , [3,5,3]
Характеристики	Обычный

В геометрии икосаэдрические соты — это одна из четырёх компактных, правильных , заполняющих пространство мозаик (или сот ) в гиперболическом 3-мерном пространстве . С символом Шлефли {3,5,3} вокруг каждого ребра находится три икосаэдра , а вокруг каждой вершины — 12 икосаэдров в правильной додекаэдрической вершинной фигуре .

Геометрические соты — это заполнение пространства многогранными или более многомерными ячейками , так что нет никаких пробелов. Это пример более общей математической мозаики или тесселяции в любом количестве измерений.

Соты обычно строятся в обычном евклидовом («плоском») пространстве, как выпуклые однородные соты . Они также могут быть построены в неевклидовых пространствах , как гиперболические однородные соты . Любой конечный однородный многогранник может быть спроецирован на его описанную сферу , чтобы сформировать однородные соты в сферическом пространстве.

Двугранный угол правильного икосаэдра составляет около 138,2°, поэтому невозможно разместить три икосаэдра вокруг ребра в евклидовом 3-пространстве. Однако в гиперболическом пространстве правильно масштабированные икосаэдры могут иметь двугранные углы ровно 120 градусов, поэтому три из них могут разместиться вокруг ребра.

В трехмерном гиперболическом пространстве имеется четыре правильных компактных соты:

Четыре правильные компактные соты в H ³

{5,3,4}

{4,3,5}

{3,5,3}

{5,3,5}

Он является членом последовательности правильных полихор и сот {3, p ,3} с дельтаэдрическими ячейками:

{3, p ,3} многогранники
Космос	С 3		Н 3
Форма	Конечный		Компактный	Паракомпактный	Некомпактный
{3, п ,3}	{3,3,3}	{3,4,3}	{3,5,3}	{3,6,3}	{3,7,3}	{3,8,3}	... {3,∞,3}
Изображение
Клетки	{3,3}	{3,4}	{3,5}	{3,6}	{3,7}	{3,8}	{3,∞}
Вершинная фигура	{3,3}	{4,3}	{5,3}	{6,3}	{7,3}	{8,3}	{∞,3}

Он также является членом последовательности правильных многогранников и сот { p ,5, p }, с вершинными фигурами, состоящими из пятиугольников:

{ p ,5, p } обычные соты
Космос	Н 3
Форма	Компактный	Некомпактный
Имя	{3,5,3}	{4,5,4}	{5,5,5}	{6,5,6}	{7,5,7}	{8,5,8}	... {∞,5,∞}
Изображение
Клетки { п ,5}	{3,5}	{4,5}	{5,5}	{6,5}	{7,5}	{8,5}	{∞,5}
Вершинная фигура {5, p }	{5,3}	{5,4}	{5,5}	{5,6}	{5,7}	{5,8}	{5,∞}

В семействе групп Коксетера [3,5,3] имеется девять однородных сот , включая эту правильную форму, а также усеченную форму, t _1,2 {3,5,3},, также называемые усеченными додекаэдрическими сотами , каждая из ячеек которых представляет собой усеченные додекаэдры .

[3,5,3] семейные соты

{3,5,3}	т 1 {3,5,3}	т 0,1 {3,5,3}	т 0,2 {3,5,3}	т 0,3 {3,5,3}
	т 1,2 {3,5,3}	т 0,1,2 {3,5,3}	т 0,1,3 {3,5,3}	т 0,1,2,3 {3,5,3}

Ректифицированные икосаэдрические соты
Тип	Равномерные соты в гиперболическом пространстве
Символ Шлефли	г{3,5,3} или т 1 {3,5,3}
Диаграмма Коксетера
Клетки	г{3,5} {5,3}
Лица	треугольник {3} пятиугольник {5}
Вершинная фигура	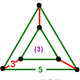треугольная призма
Группа Коксетера	${\displaystyle {\overline {J}}_{3}}$, [3,5,3]
Характеристики	Вершинно-транзитивный, реберно-транзитивный

Выпрямленные икосаэдрические соты , t ₁ {3,5,3},, имеет чередующиеся ячейки додекаэдра и икосододекаэдра , с вершинной фигурой в виде треугольной призмы :

Перспективные проекции из центра модели диска Пуанкаре

Существует четыре вида ректифицированных компактных регулярных сот:

Четыре ректифицированных регулярных компактных сот в H ³

Изображение
Символы	г{5,3,4}	г{4,3,5}	г{3,5,3}	г{5,3,5}
Вершинная фигура

Усеченные икосаэдрические соты
Тип	Равномерные соты в гиперболическом пространстве
Символ Шлефли	т{3,5,3} или т 0,1 {3,5,3}
Диаграмма Коксетера
Клетки	т{3,5} {5,3}
Лица	пятиугольник {5} шестиугольник {6}
Вершинная фигура	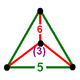треугольная пирамида
Группа Коксетера	${\displaystyle {\overline {J}}_{3}}$, [3,5,3]
Характеристики	Вершинно-транзитивный

Усеченные икосаэдрические соты , t _0,1 {3,5,3},, имеет чередующиеся ячейки додекаэдра и усеченного икосаэдра с вершиной в виде треугольной пирамиды .

Четыре усеченных правильных компактных соты в H ³

Изображение
Символы	т{5,3,4}	т{4,3,5}	т{3,5,3}	т{5,3,5}
Вершинная фигура

Усеченные икосаэдрические соты
Тип	Равномерные соты в гиперболическом пространстве
Символ Шлефли	2т{3,5,3} или т 1,2 {3,5,3}
Диаграмма Коксетера
Клетки	т{5,3}
Лица	треугольник {3} декагон {10}
Вершинная фигура	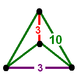тетрагональный двуклиновидный
Группа Коксетера	${\displaystyle 2\times {\overline {J}}_{3}}$, [[3,5,3]]
Характеристики	Вершинно-транзитивный, реберно-транзитивный, ячеично-транзитивный

Усеченные икосаэдрические соты , t _1,2 {3,5,3},, имеет ячейки усеченного додекаэдра с тетрагональной двуклиновидной вершинной фигурой.

Три усеченных компактных сота в H ³

Изображение
Символы	2т{4,3,5}	2т{3,5,3}	2т{5,3,5}
Вершинная фигура

Икосаэдрические соты с кантеллированными ячейками
Тип	Равномерные соты в гиперболическом пространстве
Символ Шлефли	рр{3,5,3} или т 0,2 {3,5,3}
Диаграмма Коксетера
Клетки	рр{3,5} г{5,3} {}x{3}
Лица	треугольник {3} квадрат {4} пятиугольник {5}
Вершинная фигура	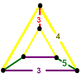клин
Группа Коксетера	${\displaystyle {\overline {J}}_{3}}$, [3,5,3]
Характеристики	Вершинно-транзитивный

Кантеллированные икосаэдрические соты , t _0,2 {3,5,3},, имеет ячейки в форме ромбоикосододекаэдра , икосододекаэдра и треугольной призмы с клиновидной вершиной.

Четыре регулярных компактных сота с кантеллированными ячейками в H 3
Изображение Символы рр{5,3,4} рр{4,3,5} рр{3,5,3} рр{5,3,5} Вершинная фигура

Усеченные икосаэдрические соты
Тип	Равномерные соты в гиперболическом пространстве
Символ Шлефли	tr{3,5,3} или t 0,1,2 {3,5,3}
Диаграмма Коксетера
Клетки	тр{3,5} т{5,3} {}x{3}
Лица	треугольник {3} квадрат {4} шестиугольник {6} десятиугольник {10}
Вершинная фигура	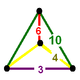зеркальный клиновидный
Группа Коксетера	${\displaystyle {\overline {J}}_{3}}$, [3,5,3]
Характеристики	Вершинно-транзитивный

Усеченные икосаэдрические соты , t _0,1,2 {3,5,3},, имеет ячейки в форме усеченного икосододекаэдра , усеченного додекаэдра и треугольной призмы с зеркально отраженной клиновидной вершиной .

Четыре усеченных регулярных компактных сотовых ячейки в H ³

Изображение
Символы	тр{5,3,4}	тр{4,3,5}	тр{3,5,3}	тр{5,3,5}
Вершинная фигура

Икосаэдрические соты с ручейковой структурой
Тип	Равномерные соты в гиперболическом пространстве
Символ Шлефли	т 0,3 {3,5,3}
Диаграмма Коксетера
Клетки	{3,5} {}×{3}
Лица	треугольник {3} квадрат {4}
Вершинная фигура	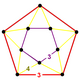пятиугольная антипризма
Группа Коксетера	${\displaystyle 2\times {\overline {J}}_{3}}$, [[3,5,3]]
Характеристики	Вершинно-транзитивный, реберно-транзитивный

Струйчатые икосаэдрические соты , t _0,3 {3,5,3},, имеет ячейки в виде икосаэдра и треугольной призмы , с вершинной фигурой в виде пятиугольной антипризмы .

Вид из центра треугольной призмы

Три регулярных компактных сотовых сота в H ³

Изображение
Символы	т 0,3 {4,3,5}	т0,3{3,5,3}	т 0,3 {5,3,5}
Вершинная фигура

Усеченные икосаэдрические соты
Тип	Равномерные соты в гиперболическом пространстве
Символ Шлефли	т 0,1,3 {3,5,3}
Диаграмма Коксетера
Клетки	т{3,5} рр{3,5} {}×{3} {}×{6}
Лица	треугольник {3} квадрат {4} пятиугольник {5} шестиугольник {6}
Вершинная фигура	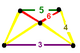равнобедренно-трапециевидная пирамида
Группа Коксетера	${\displaystyle {\overline {J}}_{3}}$, [3,5,3]
Характеристики	Вершинно-транзитивный

Усеченные икосаэдрические соты , t _0,1,3 {3,5,3},, имеет ячейки в форме усеченного икосаэдра , ромбоикосододекаэдра , шестиугольной призмы и треугольной призмы с вершиной в виде равнобедренной трапециевидной пирамиды .

Икосаэдрические соты с усеченными краями эквивалентны икосаэдрическим сотам с усеченными краями.

Вид из центра треугольной призмы

Четыре усеченных регулярных компактных сотовых ячейки в H 3
Изображение Символы т 0,1,3 {5,3,4} т 0,1,3 {4,3,5} т0,1,3{3,5,3} т 0,1,3 {5,3,5} Вершинная фигура

Всеусеченные икосаэдрические соты
Тип	Равномерные соты в гиперболическом пространстве
Символ Шлефли	т 0,1,2,3 {3,5,3}
Диаграмма Коксетера
Клетки	тр{3,5} {}×{6}
Лица	квадрат {4} шестиугольник {6} двенадцатиугольник {10}
Вершинная фигура	филлик дисфеноидный
Группа Коксетера	${\displaystyle 2\times {\overline {J}}_{3}}$, [[3,5,3]]
Характеристики	Вершинно-транзитивный

Всеусеченные икосаэдрические соты , t _0,1,2,3 {3,5,3},, имеет ячейки в форме усеченного икосододекаэдра и шестиугольной призмы , с вершинной фигурой в виде филлитового двуклиновидного треугольника.

Центрирован на шестиугольной призме

Три усеченных регулярных компактных сота в H 3
Изображение Символы т 0,1,2,3 {4,3,5} т0,1,2,3{3,5,3} т 0,1,2,3 {5,3,5} Вершинная фигура

Икосаэдрические соты Omnisnub
Тип	Равномерные соты в гиперболическом пространстве
Символ Шлефли	ч(т 0,1,2,3 {3,5,3})
Диаграмма Коксетера
Клетки	ср{3,5} с{2,3} ирр. {3,3}
Лица	треугольник {3} пятиугольник {5}
Вершинная фигура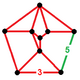
Группа Коксетера	[[3,5,3]] +
Характеристики	Вершинно-транзитивный

Всенощёкие икосаэдрические соты , h(t _0,1,2,3 {3,5,3}),, имеет ячейки плосконосого додекаэдра , октаэдра и тетраэдра с неправильной вершинной фигурой. Он вершинно-транзитивен , но не может быть создан с равномерными ячейками.

Частично уменьшенные икосаэдрические соты Парабиуменьшенные икосаэдрические соты
Тип	Равномерные соты
Символ Шлефли	пд{3,5,3}
Диаграмма Коксетера	-
Клетки	{5,3} с{2,5}
Лица	треугольник {3} пятиугольник {5}
Вершинная фигура	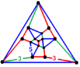тетраэдрически уменьшенный додекаэдр
Группа Коксетера	1 / 5 [3,5,3] +
Характеристики	Вершинно-транзитивный

Частично уменьшенные икосаэдрические соты или парабидоуменьшенные икосаэдрические соты , pd{3,5,3}, являются не-Витхоффовыми однородными сотами с ячейками додекаэдра и пентагональной антипризмы , с тетраэдрически уменьшенной вершинной фигурой додекаэдра . Икосаэдрические ячейки {3,5,3} уменьшены в противоположных вершинах (парабидоуменьшены), оставляя пентагональную антипризму ( парабидоуменьшенный икосаэдр ) сердцевину, и создают новые ячейки додекаэдра выше и ниже. ^{[1] [2]}

• Выпуклые однородные соты в гиперболическом пространстве
• Регулярные мозаики гиперболического 3-мерного пространства
• Пространство Зейферта–Вебера
• 11-ячеечный — абстрактный правильный полихор , имеющий общий символ Шлефли {3,5,3} .

• Коксетер , Правильные многогранники , 3-е изд., Dover Publications, 1973. ISBN 0-486-61480-8 . (Таблицы I и II: Правильные многогранники и соты, стр. 294–296) 
• Коксетер , Красота геометрии: Двенадцать эссе , Dover Publications, 1999 ISBN 0-486-40919-8 (Глава 10: Регулярные соты в гиперболическом пространстве, Сводные таблицы II, III, IV, V, стр. 212-213) 
• Норман Джонсон Однородные многогранники , Рукопись
  • NW Johnson : Теория однородных многогранников и сот , докторская диссертация, Университет Торонто, 1966 г.
  • NW Johnson: Геометрии и преобразования , (2018) Глава 13: Гиперболические группы Коксетера
• Клитцинг, Ричард. «Гиперболические соты H3 гиперболического порядка 3 икосаэдрической мозаики».