Полиномы Макдональда

В этой статье есть несколько проблем. Помогите улучшить ее или обсудите эти проблемы на странице обсуждения . ( Узнайте, как и когда удалять эти сообщения ) В статье чрезмерно много ссылок на первоисточники .Пожалуйста, улучшите эту статью, добавив вторичные или третичные источники . Найти источники:  "Многочлены Макдональда" – новости  · газеты  · книги  · ученый  · JSTOR ( Апрель 2014 )( Узнайте, как и когда удалить это сообщение ) В статье содержится список общих ссылок , но в ней отсутствуют соответствующие встроенные цитаты .Пожалуйста, помогите улучшить эту статью, добавив более точные цитаты. ( Апрель 2014 )( Узнайте, как и когда удалить это сообщение ) ( Узнайте, как и когда удалить это сообщение )

В математике полиномы Макдональда P λ ₍ x ; t , q ) представляют собой семейство ортогональных симметричных полиномов от нескольких переменных, введенных Макдональдом в 1987 году. Позднее он ввел несимметричное обобщение в 1995 году. Первоначально Макдональд связал свои полиномы с весами λ конечных систем корней и использовал только одну переменную t , но позже понял, что более естественно связывать их с аффинными системами корней, а не с конечными системами корней, и в этом случае переменную t можно заменить несколькими различными переменными t =( t ₁ ,..., t _k ), по одной для каждой из k орбит корней в аффинной системе корней. Полиномы Макдональда являются полиномами от n переменных x =( x ₁ ,..., x _n ), где n — ранг аффинной системы корней. Они обобщают многие другие семейства ортогональных многочленов, такие как многочлены Джека и многочлены Холла–Литтлвуда и многочлены Аски–Уилсона , которые в свою очередь включают большинство названных ортогональных многочленов с 1 переменной как особые случаи. Многочлены Коорнвиндера являются многочленами Макдональда определенных нередуцированных корневых систем. Они имеют глубокие связи с аффинными алгебрами Гекке и схемами Гильберта , которые использовались для доказательства нескольких гипотез , выдвинутых Макдональдом о них.

Сначала исправим некоторые обозначения:

• R — конечная корневая система в действительном векторном пространстве V.
• R ⁺ — выбор положительных корней , которому соответствует положительная камера Вейля .
• W — группа Вейля R.​
• Q — это корневая решетка R (решетка, образованная корнями).
• P — весовая решетка R (содержащая Q ).
• Упорядочение по весам : тогда и только тогда, когда является неотрицательной линейной комбинацией простых корней .${\displaystyle \mu \leq \lambda}$${\displaystyle \лямбда -\мю }$
• P ⁺ — это набор доминирующих весов: элементы P в положительной камере Вейля.
• ρ — вектор Вейля : половина суммы положительных корней; это особый элемент P ⁺ внутри положительной камеры Вейля.
• F — поле характеристики 0, обычно рациональных чисел.
• A = F ( P ) — групповая алгебра P с базисом элементов, обозначаемым e ^λ для λ ∈ P .
• Если f = e ^λ , то f означает e ^−λ , и это распространяется по линейности на всю групповую алгебру.
• m _µ = Σ _{λ ∈ W µ} e ^λ — орбитальная сумма; эти элементы образуют основу подалгебры A ^W элементов, фиксированных W .
• ${\displaystyle (a;q)_{\infty }=\prod _{r\geq 0}(1-aq^{r})}$, бесконечный символ q-Похгаммера .
• ${\displaystyle \Delta =\prod _{\alpha \in R}{(e^{\alpha };q)_{\infty } \over (te^{\alpha };q)_{\infty }}.}$
• ${\displaystyle \langle f,g\rangle =({\text{постоянный член}}f{\overline {g}}\Delta )/|W|}$является внутренним произведением двух элементов A , по крайней мере, когда t является положительной целой степенью q .

Полиномы Макдональда P _λ для λ ∈ P ⁺ однозначно определяются следующими двумя условиями:

${\displaystyle P_{\lambda }=\sum _{\mu \leq \lambda }u_ {\lambda \mu }m_ {\mu }}$где u _λμ — рациональная функция q и t с u _λλ = 1;

P _λ и P _µ ортогональны, если λ < µ.

Другими словами, полиномы Макдональда получаются путем ортогонализации очевидного базиса для A ^W . Существование полиномов с этими свойствами легко показать (для любого скалярного произведения). Ключевым свойством полиномов Макдональда является то, что они ортогональны : 〈P _λ , P _μ〉 = 0 всякий раз, когда λ ≠ μ. Это не тривиальное следствие определения, поскольку P ⁺ не является полностью упорядоченным и поэтому имеет множество элементов, которые несравнимы. Таким образом, необходимо проверить, что соответствующие полиномы по-прежнему ортогональны. Ортогональность можно доказать, показав, что полиномы Макдональда являются собственными векторами для алгебры коммутирующих самосопряженных операторов с одномерными собственными пространствами, и используя тот факт, что собственные пространства для различных собственных значений должны быть ортогональны.

В случае непростых корневых систем (B, C, F, G) параметр t может быть выбран так, чтобы он менялся в зависимости от длины корня, что дает трехпараметрическое семейство полиномов Макдональда. Можно также расширить определение до нередуцированной корневой системы BC, в этом случае получится шестипараметрическое семейство (один t для каждой орбиты корней, плюс q ), известное как полиномы Коорнвиндера . Иногда лучше рассматривать полиномы Макдональда как зависящие от возможно нередуцированной аффинной корневой системы. В этом случае с каждой орбитой корней в аффинной корневой системе связан один параметр t , плюс один параметр q . Количество орбит корней может варьироваться от 1 до 5.

• Если q = t, то многочлены Макдональда становятся характерами Вейля представлений компактной группы корневой системы или функциями Шура в случае корневых систем типа A.
• Если q = 0 , то полиномы Макдональда становятся (масштабированными) зональными сферическими функциями для полупростой p -адической группы или полиномами Холла–Литтлвуда, когда корневая система имеет тип A.
• Если t = 1, то полиномы Макдональда становятся суммами по W орбитам, которые являются мономиальными симметричными функциями, когда корневая система имеет тип A.
• Если положить t = q ^α и устремить q к 1, то полиномы Макдональда станут полиномами Джека , когда корневая система имеет тип A , и полиномами Хекмана–Опдама для более общих корневых систем.
• Для аффинной корневой системы A ₁ полиномы Макдональда являются полиномами Роджерса .
• Для нередуцированной аффинной корневой системы ранга 1 типа ( C^∨
  ₁, C ₁ ), полиномы Макдональда являются полиномами Аски–Уилсона , которые, в свою очередь, включают в себя в качестве частных случаев большинство названных семейств ортогональных полиномов от одной переменной.
• Для нередуцированной аффинной корневой системы типа ( C^∨
  _н, C _n ), полиномы Макдональда являются полиномами Коорнвиндера .

Если t = q ^k для некоторого положительного целого числа k , то норма полиномов Макдональда определяется выражением

${\displaystyle \langle P_{\lambda },P_{\lambda }\rangle =\prod _{\alpha \in R,\alpha >0}\prod _{0<i<k}{1-q^{(\lambda +k\rho ,2\alpha /(\alpha ,\alpha ))+i} \over 1-q^{(\lambda +k\rho ,2\alpha /(\alpha ,\alpha ))-i}}.}$

Это было высказано Макдональдом (1982) как обобщение гипотезы Дайсона и доказано для всех (редуцированных) корневых систем Чередником (1995) с использованием свойств двойных аффинных алгебр Гекке . Гипотеза ранее была доказана по каждому случаю для всех корневых систем, за исключением систем типа E _n несколькими авторами.

Существуют две другие гипотезы, которые вместе с гипотезой о норме в этом контексте называются гипотезами Макдональда: в дополнение к формуле для нормы Макдональд предположил формулу для значения P _λ в точке t ^ρ и симметрию

${\displaystyle {\frac {P_{\lambda }(\dots ,q^{\mu _{i}}t^{\rho _{i}},\dots )}{P_{\lambda }(t^{\rho })}}={\frac {P_{\mu }(\dots ,q^{\lambda _{i}}t^{\rho _{i}},\dots )}{P_{\mu }(t^{\rho })}}.}$

Опять же, эти утверждения были доказаны для общих редуцированных корневых систем Чередником (  1995) с использованием двойных аффинных алгебр Гекке , а вскоре после этого были распространены на случай BC в работах ван Диегона, Ноуми и Сахи.

В случае систем корней типа A _{n −1} полиномы Макдональда являются просто симметричными полиномами от n переменных с коэффициентами, которые являются рациональными функциями от q и t . Определенная преобразованная версия полиномов Макдональда (см. Комбинаторную формулу ниже) образует ортогональный базис пространства симметричных функций над и, следовательно, может быть выражена в терминах функций Шура . Коэффициенты K _λμ ( q , t ) этих соотношений называются коэффициентами Костки–Макдональда или qt -коэффициентами Костки. Макдональд предположил, что коэффициенты Костки–Макдональда были полиномами от q и t с неотрицательными целыми коэффициентами. Эти гипотезы теперь доказаны; самым сложным и последним шагом было доказательство положительности, что было сделано Марком Хайманом (2001), доказав гипотезу n ! .${\displaystyle {\widetilde {H}}_{\mu }}$${\displaystyle \mathbb {Q} (q,t)}$ ${\displaystyle s_{\lambda }}$

Нахождение комбинаторной формулы для коэффициентов qt -Костки по-прежнему остается центральной открытой проблемой алгебраической комбинаторики .

Гипотеза n ! Адриано Гарсии и Марка Хаймана утверждает, что для каждого разбиения μ числа n пространство

${\displaystyle D_{\mu }=C[\partial _{x},\partial _{y}]\,\Delta _{\mu }}$

охватывается всеми высшими частными производными

${\displaystyle \Delta _{\mu }=\det(x_{i}^{p_{j}}y_{i}^{q_{j}})_{1\leq i,j,\leq n}}$

имеет размерность n !, где ( p _j , q _j ) пробегают n элементов диаграммы разбиения μ, рассматриваемого как подмножество пар неотрицательных целых чисел. Например, если μ — разбиение 3 = 2 + 1 n  = 3, то пары ( p _j , q _j ) равны (0, 0), (0, 1), (1, 0), а пространство D _μ охватывается

${\displaystyle \Delta _{\mu }=x_{1}y_{2}+x_{2}y_{3}+x_{3}y_{1}-x_{2}y_{1}-x_{3}y_{2}-x_{1}y_{3}}$

${\displaystyle y_{2}-y_{3}}$

${\displaystyle y_{3}-y_{1}}$

${\displaystyle x_{3}-x_{2}}$

${\displaystyle x_{1}-x_{3}}$

${\displaystyle 1}$

который имеет размерность 6 = 3!.

Доказательство Хаймана гипотезы о положительности Макдональда и гипотезы n ! включало демонстрацию того, что изоспектральная схема Гильберта n точек на плоскости была схемой Коэна–Маколея (и даже Горенштейна ). Более ранние результаты Хаймана и Гарсии уже показали, что это подразумевало гипотезу n !, и что гипотеза n ! подразумевала, что коэффициенты Костки–Макдональда были градуированными кратностями характеров для модулей D _μ . Это немедленно влечет гипотезу о положительности Макдональда, поскольку кратности характеров должны быть неотрицательными целыми числами.

Ян Гройновски и Марк Хайман нашли еще одно доказательство гипотезы Макдональда о положительности, доказав гипотезу о положительности для полиномов LLT .

В 2005 году Дж. Хаглунд, М. Хайман и Н. Лёр ^[1] дали первое доказательство комбинаторной интерпретации полиномов Макдональда. В 1988 году И. Г. Макдональд ^[2] дал второе доказательство комбинаторной интерпретации полиномов Макдональда (уравнения (4.11) и (5.13)). Формула Макдональда отличается от формулы в работе Хаглунда, Хаймана и Лёра, с гораздо меньшим количеством членов (эта формула также доказана в основополагающей работе Макдональда, ^[3] гл. VI (7.13)). Хотя они очень полезны для вычислений и интересны сами по себе, их комбинаторные формулы не подразумевают сразу положительность коэффициентов Костки-Макдональда, поскольку дают разложение полиномов Макдональда на мономиальные симметричные функции, а не на функции Шура.${\displaystyle K_{\lambda \mu }(q,t),}$

Записанные в преобразованных полиномах Макдональда , а не в обычных , они имеют вид${\displaystyle {\widetilde {H}}_{\mu }}$${\displaystyle P_{\lambda }}$

${\displaystyle {\widetilde {H}}_{\mu }(x;q,t)=\sum _{\sigma :\mu \to \mathbb {Z} _{+}}q^{inv(\sigma )}t^{maj(\sigma )}x^{\sigma }}$

где σ — заполнение диаграммы Юнга формы μ, inv и maj — некоторые комбинаторные статистики (функции), определенные на заполнении σ. Эта формула выражает полиномы Макдональда от бесконечного числа переменных. Чтобы получить полиномы от n переменных, просто ограничьте формулу заполнениями, которые используют только целые числа 1, 2, ..., n . Член x ^σ следует интерпретировать как где σ _i — количество ячеек в заполнении μ с содержимым i .${\displaystyle x_{1}^{\sigma _{1}}x_{2}^{\sigma _{2}}\cdots }$

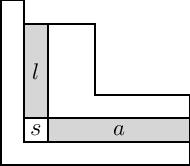
Преобразованные полиномы Макдональда в приведенной выше формуле связаны с классическими полиномами Макдональда через последовательность преобразований. Во-первых, интегральная форма полиномов Макдональда, обозначенная , является перемасштабированием , которое очищает знаменатели коэффициентов:${\displaystyle {\widetilde {H}}_{\mu }(x;q,t)}$${\displaystyle P_{\lambda }}$${\displaystyle J_{\lambda }(x;q,t)}$${\displaystyle P_{\lambda }(x;q,t)}$

${\displaystyle J_{\lambda }(x;q,t)=\prod _{s\in D(\lambda )}(1-q^{a(s)}t^{1+l(s)})\cdot P_{\lambda }(x;q,t)}$

где — набор квадратов в диаграмме Юнга , а и обозначают плечо и ногу квадрата , как показано на рисунке. Примечание: На рисунке справа используется французская нотация для tableau, которая перевернута по вертикали относительно английской нотации, используемой на странице Википедии для диаграмм Юнга. Французская нотация чаще используется при изучении полиномов Макдональда.${\displaystyle D(\lambda )}$${\displaystyle \lambda }$${\displaystyle a(s)}$${\displaystyle l(s)}$${\displaystyle s}$

Преобразованные полиномы Макдональда затем можно определить в терминах 's. Мы имеем${\displaystyle {\widetilde {H}}_{\mu }(x;q,t)}$${\displaystyle J_{\mu }}$

${\displaystyle {\widetilde {H}}_{\mu }(x;q,t)=t^{-n(\mu )}J_{\mu }\left[{\frac {X}{1-t^{-1}}};q,t^{-1}\right]}$

где

${\displaystyle n(\mu )=\sum _{i}\mu _{i}\cdot (i-1).}$

Обозначение в скобках выше обозначает плетистическую замену .

Эту формулу можно использовать для доказательства формулы Кнопа и Сахи для полиномов Джека .

В 1995 году Макдональд ввел несимметричный аналог симметричных полиномов Макдональда, и симметричные полиномы Макдональда можно легко восстановить из несимметричного аналога. В своем первоначальном определении он показывает, что несимметричные полиномы Макдональда являются уникальным семейством полиномов, ортогональных определенному внутреннему произведению, а также удовлетворяющих свойству треугольности при разложении в мономиальном базисе.

В 2007 году Хаглунд, Хайман и Лёр дали комбинаторную формулу для несимметричных полиномов Макдональда.

Несимметричные полиномы Макдональда специализируются на символах Демазюра, принимая q=t=0, и на ключевых полиномах, когда q=t=∞.

В 2018 году С. Кортил , О. Мандельштам и Л. Уильямс использовали процесс исключения, чтобы дать прямую комбинаторную характеристику как симметричных, так и несимметричных полиномов Макдональда. ^[4] Их результаты отличаются от более ранней работы Хаглунда отчасти тем, что они дают формулу непосредственно для полиномов Макдональда, а не их преобразование. Они развивают концепцию многолинейной очереди, которая представляет собой матрицу, содержащую шары или пустые ячейки вместе с отображением между шарами и их соседями и комбинаторным механизмом маркировки. Тогда несимметричный полином Макдональда удовлетворяет:

${\displaystyle E_{\lambda }({\textbf {x}};q,t)=\sum _{Q}\mathrm {wt} (Q)}$

где сумма берется по всем многострочным очередям типа и является весовой функцией, отображающей эти очереди в определенные полиномы. Симметричный полином Макдональда удовлетворяет:${\displaystyle L\times n}$${\displaystyle \lambda }$${\displaystyle \mathrm {wt} }$

${\displaystyle P_{\lambda }({\textbf {x}};q,t)=\sum _{\mu }E_{\mu }(x_{1},...,x_{n};q,t)=\sum _{\mu }\sum _{Q}\mathrm {wt} (Q)}$

где внешняя сумма берется по всем различным композициям , которые являются перестановками , а внутренняя сумма такая же, как и прежде.${\displaystyle \mu }$${\displaystyle \lambda }$

• Чередник, Иван (1995), «Двойные аффинные алгебры Гекке и гипотезы Макдональда», Annals of Mathematics , вторая серия, 141 (1), Annals of Mathematics: 191– 216, doi : 10.2307/2118632, ISSN  0003-486X, JSTOR  2118632
• Гарсия, Адриано; Реммель, Джеффри Б. (15 марта 2005 г.), « Прорывы в теории полиномов Макдональда », PNAS , 102 (11): 3891– 3894, Bibcode : 2005PNAS..102.3891G, doi : 10.1073/pnas.0409705102 , PMC  554818 , PMID  15753285
• Марк Хайман Комбинаторика, симметричные функции и схемы Гильберта. Текущие разработки в математике 2002, № 1 (2002), 39–111.
• Хайман, Марк Заметки о полиномах Макдональда и геометрии схем Гильберта. Симметричные функции 2001: обзоры разработок и перспектив, 1–64, NATO Sci. Ser. II Math. Phys. Chem., 74, Kluwer Acad. Publ., Dordrecht, 2002. MR 2059359
• Хайман, Марк (2001), « Схемы Гильберта, полиграфы и гипотеза Макдональда о позитивности », J. Amer. Math. Soc. , 14 (4): 941–1006 , arXiv : math.AG/0010246 , doi :10.1090/S0894-0347-01-00373-3, S2CID  9253880
• Кириллов, АА (1997), "Лекции по аффинным алгебрам Гекке и гипотезам Макдональда", Bull. Amer. Math. Soc. , 34 (3): 251– 292, doi : 10.1090/S0273-0979-97-00727-1
• Macdonald, IG (1982), «Некоторые гипотезы для корневых систем», SIAM Journal on Mathematical Analysis , 13 (6): 988– 1007, doi :10.1137/0513070, ISSN  0036-1410, MR  0674768
• Macdonald, IG Симметричные функции и многочлены Холла. Второе издание. Oxford Mathematical Monographs. Oxford Science Publications. The Clarendon Press, Oxford University Press, Нью-Йорк, 1995. x+475 стр. ISBN 0-19-853489-2 MR 1354144 
• Macdonald, IG Симметричные функции и ортогональные многочлены. Лекции памяти декана Жаклин Б. Льюис, прочитанные в Университете Ратгерса, Нью-Брансуик, Нью-Джерси. Серия университетских лекций, 12. Американское математическое общество, Провиденс, Род-Айленд, 1998. xvi+53 стр. ISBN 0-8218-0770-6 MR 1488699 
• Макдональд, И.Г. Аффинные алгебры Гекке и ортогональные многочлены. Семинар Бурбаки 797 (1995).
• Макдональд, И.Г. (2000–2001), «Ортогональные полиномы, связанные с корневыми системами», Séminaire Lotharingien de Combinatoire , 45 : Art. B45a, arXiv : math.QA/0011046 , MR  1817334
• Macdonald, IG (2003), Аффинные алгебры Гекке и ортогональные многочлены , Cambridge Tracts in Mathematics, т. 157, Кембридж: Cambridge University Press, стр. x+175, ISBN 978-0-521-82472-9, МР  1976581

• Страница Майка Заброцкого о полиномах Макдональда.
• Некоторые статьи Хаймана о полиномах Макдональда.