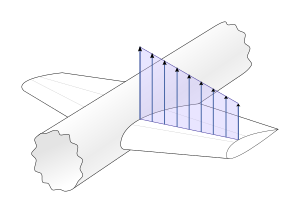
- Распределение подъемной силы по крылу можно смоделировать с помощью концепции циркуляции.
- Вихрь образуется ниже по потоку при каждом изменении подъемной силы по размаху.
Теория подъемной линии
Теория подъемной линии Ланчестера-Прандтля [ 1] — это математическая модель в аэродинамике , которая предсказывает распределение подъемной силы по трехмерному крылу из геометрии крыла . [2] Теория была выражена независимо [3] Фредериком В. Ланчестером в 1907 году [4] и Людвигом Прандтлем в 1918–1919 годах [5] после работы с Альбертом Бецом и Максом Мунком . В этой модели вихрь, связанный с крылом, развивается по всему размаху крыла, поскольку он сбрасывается как вихревая пелена с задней кромки, а не просто как одиночный вихрь с законцовок крыла. [6] [7]
Введение
.jpg/440px-1915ca_laminar_fluegel(cropped).jpg)
Трудно аналитически предсказать общую величину подъемной силы, которую будет генерировать крыло заданной геометрии. При анализе трехмерного конечного крыла традиционный подход разрезает крыло на поперечные сечения и анализирует каждое поперечное сечение независимо как крыло в двумерном мире. Каждый из этих срезов называется аэродинамическим профилем , и легче понять аэродинамический профиль, чем полное трехмерное крыло.
Можно было бы ожидать, что понимание полного крыла просто включает в себя сложение независимо рассчитанных сил от каждого сегмента аэродинамического профиля. Однако это приближение является грубо неверным: на реальном крыле подъемная сила от каждой бесконечно малой секции крыла сильно зависит от воздушного потока над соседними секциями крыла. Теория подъемной линии исправляет некоторые ошибки в наивном двумерном подходе, включая некоторые взаимодействия между секциями крыла.
- Нереалистичное распределение подъемной силы, не учитывающее трехмерные эффекты
- Наблюдаемое распределение подъемной силы на (конечном) трапециевидном крыле
Принцип и происхождение
Теория подъемной линии предполагает крылья, которые являются длинными и тонкими с незначительным фюзеляжем , похожими на тонкий стержень (одноименный «подъемный стержень») размахом 2 s, движущийся через жидкость. Из теоремы Кутты-Жуковского , подъемная сила L ( y ) на 2-мерном сегменте крыла на расстоянии y от фюзеляжа пропорциональна циркуляции Γ ( y ) вокруг стержня в y . Когда самолет неподвижен на земле, эти циркуляции все равны, но когда судно находится в движении, они изменяются с y . По теоремам Гельмгольца , генерация пространственно-изменяющейся циркуляции должна соответствовать испусканию вихревой нити равной прочности вниз по потоку от крыла . [8]
В теории подъемной линии предполагается, что образующаяся вихревая линия остается связанной с крылом , так что она изменяет эффективный вертикальный угол входящего свободного потока воздуха.
Вертикальное движение, вызванное вихревой линией силы γ в воздухе на расстоянии r, равно γ ⁄ 4π r , так что вся вихревая система вызывает вертикальное движение свободного потока в положении y , где интеграл понимается в смысле главного значения Коши . Этот поток изменяет эффективный угол атаки в y ; если реакция циркуляции аэродинамических профилей, составляющих крыло, понимается в диапазоне углов атаки, то можно разработать интегральное уравнение для определения Γ( y ) . [9]
Формально, существует некоторый угол ориентации, такой, что аэродинамический профиль в положении y не развивает подъемной силы. Для воздушных потоков со скоростью V, ориентированных под углом α относительно угла без подъемной силы, аэродинамический профиль будет развивать некоторую циркуляцию V ⋅ C ( y ,α) ; для малых α разложение Тейлора приближает эту циркуляцию как V ⋅ ∂ C ⁄ ∂α ( y ,0)⋅α . Если аэродинамический профиль идеален и имеет хорду c ( y ) , то теория предсказывает это, но реальные аэродинамические профили могут быть менее эффективными. [10] [11]
Предположим, что свободный поток атакует аэродинамический профиль в позиции y под углом α( y ) (относительно угла без подъемной силы для аэродинамического профиля в позиции y — таким образом, равномерный поток через крыло может все еще иметь изменяющийся α( y ) ). В приближении малого угла эффективный угол атаки в y объединенной системы свободного потока и вихря равен α( y )+ w ( y ) ⁄ V . Объединяя приведенные выше формулы,
| ( 1 ) |
Все величины в этом уравнении, за исключением V и Γ, являются геометрическими свойствами крыла, и поэтому инженер может (в принципе) решить для Γ( y ) при фиксированном V . Как и при выводе теории тонкого аэродинамического профиля , распространенный подход заключается в разложении Γ в ряд Фурье вдоль крыла, а затем сохранении только первых нескольких членов. [12] [13] [14]
После того, как скорость V , циркуляция Γ и плотность жидкости ρ известны, подъемная сила, создаваемая крылом, принимается равной чистой подъемной силе, создаваемой каждым аэродинамическим профилем с заданной циркуляцией... ...а сопротивление также является общим по аэродинамическим профилям: Из этих величин и соотношения сторон AR можно вычислить коэффициент эффективности размаха. [ 15 ] [16] [11]
Эффекты управляющих входов
Отклонение управляющей поверхности изменяет форму каждого среза аэродинамического профиля, что может привести к разным углам отсутствия подъемной силы для этого аэродинамического профиля, а также к разным углам атаки. Это не требует существенных изменений в теории, а только изменения ∂ α C ( y ,0) и α( y ) в ( 1 ). Однако тело с быстро движущимися крыльями, такое как катящийся самолет или машущая птица, испытывает вертикальный поток через крыло из-за изменения ориентации крыла, что появляется как отсутствующий член в теории.
Вращающиеся крылья
Когда самолет вращается со скоростью p вокруг фюзеляжа, аэродинамический профиль в ( обозначенном ) положении y испытывает вертикальный поток воздуха со скоростью py , который соответственно добавляет py ⁄ V к эффективному углу атаки. Таким образом, ( 1 ) становится: что соответственно изменяет как подъемную силу, так и индуцированное сопротивление. [17] Эта «сила сопротивления» составляет основное производство тяги для машущих крыльев. [17]
Эллиптические крылья
Эффективность e теоретически оптимизируется в эллиптическом крыле без закручивания, в котором θ — альтернативная параметризация станции вдоль крыла. Для такого крыла, которое дает уравнение для эллиптического коэффициента индуцированного сопротивления: Согласно теории подъемной линии, любая форма крыла в плане может достичь той же эффективности за счет закручивания (изменение положения в зависимости от увеличения шага ) относительно фюзеляжа. [14]
Полезные приближения
Полезное приближение для трехмерного коэффициента подъемной силы для эллиптического распределения циркуляции [ требуется ссылка ]: Обратите внимание, что это уравнение становится уравнением тонкого аэродинамического профиля , если AR стремится к бесконечности. [18] [ неудачная проверка ]
Ограничения
Теория подъемной линии не учитывает сжатие воздуха крыльями, вязкое течение в пограничном слое фюзеляжа или формы крыльев, отличные от длинных, прямых и тонких, таких как стреловидные или крылья с малым удлинением . Теория также предполагает, что поток вокруг крыльев находится в равновесии , и не рассматривает тела, которые быстро ускоряются относительно свободного потока воздуха.
Смотрите также
- Подковообразный вихрь
- Состояние Кутта
- Теория тонкого аэродинамического профиля
- Метод вихревой решетки
- Уравнения Эйлера (гидродинамика)
Примечания
- ^ Андерсон, Джон Д. (2001), Основы аэродинамики , стр. 360. McGraw-Hill, Бостон. ISBN 0-07-237335-0 .
- ^ Houghton, EL; Carpenter, PW (2003). Butterworth Heinmann (ред.). Аэродинамика для студентов-инженеров (5-е изд.). ISBN 0-7506-5111-3.
- ^ фон Карман, Теодор (2004) [1954]. Аэродинамика: избранные темы в свете их исторического развития . Дувр. ISBN 0-486-43485-0.
- ^ Ланчестер, Фредерик В. (1907). Констебль (ред.). Аэродинамика.
- ^ Прандтль, Людвиг (1918). Königliche Gesellschaft der Wissenschaften zu Göttingen (ред.). Трагфлюгельная теория .
- ^ Эбботт, Айра Х. и Фон Денхофф, Альберт Э., Теория сечений крыла , раздел 1.4.
- ^ Клэнси, Л.Дж., Аэродинамика , Раздел 8.11.
- ^ Batchelor, G. K. (1993) [1967]. Введение в гидродинамику (3-е индийское переиздание). Нью-Дели: Cambridge University Press (опубликовано в 2014 г.). стр. 580–585. ISBN 978-81-85618-24-1.
- ↑ Бэтчелор 1993, стр. 585-586.
- ^ Ачесон, Д. Дж. (1990). Элементарная гидродинамика . Оксфордская прикладная математика и вычислительная наука. Оксфорд: Clarendon Press (опубликовано в 2009 г.). С. 134–136, 138.
- ^ ab Auld, Douglass; Srinivas (1995). «Трехмерная теория подъемной линии». Аэродинамика для студентов. Сиднейский университет.
- ↑ Бэтчелор 1993, стр. 586-587.
- ^ Филлипс, Уоррен; Элли, Николас; Гудрич, Уэйн (2003-06-23), "Анализ подъемной линии управления креном и переменной круткой", 21-я конференция AIAA по прикладной аэродинамике , конференции по гидродинамике и смежным дисциплинам, Американский институт аэронавтики и астронавтики, doi :10.2514/6.2003-4061, ISBN 978-1-62410-092-5, получено 2020-12-02
- ^ ab Phillips, WF (2004-01-01). «Анализ подъемной линии для скрученных крыльев и крыльев, оптимизированных для вымывания». Journal of Aircraft . 41 (1): 128–136. doi :10.2514/1.262.
- ^ Эбботт, Айра Х. и Фон Денхофф, Альберт Э., Теория сечений крыла , Раздел 1.3
- ^ Клэнси, Л.Дж., Аэродинамика , Уравнение 5.7
- ^ ab Phillips, WF (2014-02-28). «Аналитическое разложение крена и взмахов крыла с использованием теории подъемной линии». Journal of Aircraft . 51 (3): 761–778. doi :10.2514/1.C032399.
- ^ Скотт, Джефф (10 августа 2003 г.). «Вопрос № 136: Коэффициент подъемной силы и теория тонкого аэродинамического профиля». Спросите ракетчика: Аэродинамика. Aerospaceweb.org.
Ссылки
- LJ Clancy (1975), Аэродинамика , Pitman Publishing Limited, Лондон. ISBN 0-273-01120-0
- Эбботт, Айра Х. и фон Денхофф, Альберт Э. (1959), Теория сечений крыла , Dover Publications Inc., Нью-Йорк. Стандартный номер книги 486-60586-8