Клаус Рот

Клаус Рот
Рожденный	Клаус Фридрих Рот ( 1925-10-29 )29 октября 1925 г. Бреслау , провинция Нижняя Силезия , Веймарская Германия
Умер	10 ноября 2015 г. (2015-11-10)(90 лет) Инвернесс , Шотландия
Образование	Школа Святого Павла, Лондон Питерхаус, Кембридж Университетский колледж Лондона
Известный	Диофантово приближение Теория расхождений Большое сито
Награды	Медаль Филдса (1958) Член Королевского общества (1960) Медаль Де Моргана (1983) Медаль Сильвестра (1991)
Научная карьера
Поля	Математика
Учреждения	Университетский колледж Лондона Имперский колледж Лондона
Тезис	Доказательство того, что почти все положительные целые числа являются суммами квадрата, положительного куба и четвертой степени  (1950)
научный руководитель	Теодор Эстерманн
Другие научные консультанты	Джон Чарльз Беркилл Гарольд Дэвенпорт

Клаус Фридрих Рот FRS (29 октября 1925 – 10 ноября 2015) был британским математиком немецкого происхождения, который выиграл медаль Филдса за доказательство теоремы Рота о диофантовых приближениях алгебраических чисел . Он также был обладателем медали Де Моргана и медали Сильвестра , а также членом Королевского общества .

Рот переехал в Англию в детстве в 1933 году, чтобы спастись от нацистов, и получил образование в Кембриджском университете и Лондонском университетском колледже , защитив докторскую диссертацию в 1950 году. Он преподавал в Лондонском университетском колледже до 1966 года, когда занял кафедру в Имперском колледже Лондона . Он вышел на пенсию в 1988 году.

Помимо работы над диофантовыми приближениями, Рот внес большой вклад в теорию множеств без прогрессий в арифметической комбинаторике и в теорию нерегулярностей распределения . Он также был известен своими исследованиями по суммам степеней , по большому решету , по проблеме треугольников Хейльбронна и по упаковке квадратов в квадрате . Он был соавтором книги Sequences on integer sequences .

Рот родился в еврейской семье в Бреслау , Пруссия , 29 октября 1925 года. Его родители поселились с ним в Лондоне, чтобы избежать нацистских преследований в 1933 году, и он был воспитан и получил образование в Великобритании. ^{[1] [2]} Его отец, адвокат, подвергся воздействию отравляющего газа во время Первой мировой войны и умер, когда Рот был еще маленьким. Рот стал учеником школы Святого Павла в Лондоне с 1939 по 1943 год, и вместе с остальной частью школы он был эвакуирован из Лондона в Истхэмпстед-парк во время Блица . В школе он был известен своими способностями как в шахматах, так и в математике. Он пытался присоединиться к Корпусу воздушной подготовки , но был заблокирован в течение нескольких лет из-за того, что был немцем, а затем после этого из-за отсутствия координации, необходимой для пилота. ^[2]

Рот изучал математику в Peterhouse, Cambridge , и играл на первой доске за шахматную команду Кембриджа, ^[2] закончив в 1945 году. ^[3] Несмотря на свои навыки в математике, он получил только третьестепенные оценки на Mathematical Tripos из-за его слабых способностей к сдаче тестов. Его кембриджский наставник, Джон Чарльз Беркилл , не поддерживал продолжение Ротом математики, рекомендуя ему вместо этого заняться «какой-нибудь коммерческой работой со статистическим уклоном». ^[2] Вместо этого он недолгое время работал школьным учителем в Гордонстоуне , между окончанием Кембриджа и началом аспирантуры. ^{[1] [2]}

По рекомендации Гарольда Дэвенпорта он был принят в 1946 году в магистратуру по математике в Университетском колледже Лондона , где он работал под руководством Теодора Эстерманна . ^[2] Он получил там степень магистра в 1948 году и докторскую степень в 1950 году. ^[3] Его диссертация была «Доказательство того, что почти все положительные целые числа являются суммами квадрата, положительного куба и четвертой степени» . ^[4]

Получив степень магистра в 1948 году, Рот стал ассистентом лектора в Университетском колледже Лондона, а в 1950 году он был повышен до лектора. ^[5] Его самые значительные вклады в диофантовы приближения, последовательности без прогрессии и расхождения были опубликованы в середине 1950-х годов, и к 1958 году он был удостоен Медали Филдса, высшей награды математиков. ^{[2] [6]} Однако только в 1961 году он был повышен до должности полного профессора. ^[1] В этот период он продолжал тесно сотрудничать с Гарольдом Дэвенпортом. ^[2]

Он брал академические отпуска в Массачусетском технологическом институте в середине 1950-х и середине 1960-х годов и серьезно рассматривал возможность переезда в Соединенные Штаты. Уолтер Хейман и Патрик Линстед противостояли этой возможности, которую они считали угрозой британской математике, предложением кафедры чистой математики в Имперском колледже Лондона , и Рот принял кафедру в 1966 году. ^[2] Он сохранял эту должность до официального выхода на пенсию в 1988 году. ^[1] Он оставался в Имперском колледже в качестве приглашенного профессора до 1996 года. ^[3]

Лекции Рота обычно были очень ясными, но иногда могли быть беспорядочными. ^[2] Проект генеалогии математики указывает, что у него было всего два аспиранта, ^[4] но один из них, Уильям Чен, продолживший работу Рота в теории расхождений, стал членом Австралийского математического общества и главой математического факультета в Университете Маккуори . ^[7]

В 1955 году Рот женился на Мелек Хайри, которая привлекла его внимание, когда она была студенткой на его первой лекции; Хайри была дочерью египетского сенатора Хайри Паши ^{[1] [2]} Она пришла работать на факультет психологии в Университетском колледже Лондона, где опубликовала исследование о влиянии токсинов на крыс. ^[8] После выхода Рота на пенсию они переехали в Инвернесс ; Рот посвятил комнату своего дома латинским танцам, их общему увлечению. ^{[2] [9]} Хайри умерла в 2002 году, а Рот умер в Инвернессе 10 ноября 2015 года в возрасте 90 лет. ^{[1] [2] [3]} У них не было детей, и Рот посвятил большую часть своего состояния, более миллиона фунтов, двум благотворительным организациям здравоохранения «для помощи пожилым и немощным людям, живущим в городе Инвернесс». Он отправил медаль Филдса с меньшим завещанием Питерхаусу. ^[10]

Рот был известен как решатель проблем в математике, а не как создатель теорий. Гарольд Дэвенпорт пишет, что «мораль работы доктора Рота» заключается в том, что «великие нерешенные проблемы математики все еще могут поддаться прямой атаке, какими бы сложными и неприступными они ни казались, и сколько бы усилий на них уже ни было потрачено». ^[6] Его исследовательские интересы охватывали несколько тем в теории чисел , теории расхождений и теории целочисленных последовательностей .

Предмет диофантовых приближений ищет точные приближения иррациональных чисел рациональными числами . Вопрос о том, насколько точно алгебраические числа могут быть приближены, стал известен как проблема Туэ–Зигеля после предыдущего прогресса в этом вопросе Акселя Туэ и Карла Людвига Зигеля . Точность приближения может быть измерена показателем приближения числа , определяемым как наибольшее число , которое имеет бесконечно много рациональных приближений с . Если показатель приближения велик, то имеет более точные приближения, чем число, показатель степени которого меньше. Наименьший возможный показатель приближения равен двум: даже самые трудно приближаемые числа можно приблизить показателем два с помощью цепных дробей . ^{[3] [6]} До работы Рота считалось, что алгебраические числа могут иметь больший показатель приближения, связанный со степенью многочлена , определяющего число. ^[2]${\displaystyle x}$${\displaystyle е}$${\displaystyle x}$${\displaystyle п/д}$${\displaystyle |xp/q|<1/q^{e}}$${\displaystyle x}$

В 1955 году Рот опубликовал то, что сейчас известно как теорема Рота , полностью разрешив этот вопрос. Его теорема опровергла предполагаемую связь между показателем аппроксимации и степенью и доказала, что с точки зрения показателя аппроксимации алгебраические числа являются наименее точно аппроксимируемыми из любых иррациональных чисел. Точнее, он доказал, что для иррациональных алгебраических чисел показатель аппроксимации всегда равен двум. ^[3] В обзоре работы Рота, представленном Гарольдом Дэвенпортом Международному конгрессу математиков в 1958 году, когда Роту была вручена медаль Филдса, Дэвенпорт назвал этот результат «величайшим достижением» Рота. ^[6]

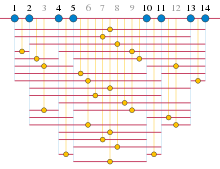
Другой результат, называемый « теоремой Рота », полученный в 1953 году, относится к арифметической комбинаторике и касается последовательностей целых чисел без тройки в арифметической прогрессии . Эти последовательности изучались в 1936 году Полом Эрдёшем и Палом Тураном , которые предположили, что они должны быть разреженными. ^{[11] [a]} Однако в 1942 году Рафаэль Салем и Дональд С. Спенсер построили подмножества чисел от до , свободные от прогрессии, размером пропорциональным , для каждого . ^[12]${\displaystyle 1}$${\displaystyle n}$${\displaystyle n^{1-\varepsilon }}$${\displaystyle \varepsilon >0}$

Рот оправдал Эрдёша и Турана, доказав, что размер такого множества не может быть пропорционален : каждое плотное множество целых чисел содержит трехчленную арифметическую прогрессию. Его доказательство использует методы из аналитической теории чисел , включая метод круга Харди–Литтлвуда, чтобы оценить количество прогрессий в заданной последовательности и показать, что когда последовательность достаточно плотная, это число не равно нулю. ^{[2] [13]}${\displaystyle n}$

Другие авторы позже усилили границу Рота относительно размера множеств без прогрессий. ^[14] Усиление в другом направлении, теорема Семереди , показывает, что плотные множества целых чисел содержат произвольно длинные арифметические прогрессии. ^[15]

Хотя работа Рота по диофантовым приближениям принесла ему наибольшее признание, именно его исследования нерегулярностей распределения (согласно некрологу Уильяма Чена и Боба Вогана ) стали предметом его наибольшей гордости. ^[2] Его работа 1954 года по этой теме заложила основы современной теории расхождений . Она касается размещения точек в единичном квадрате таким образом, чтобы для каждого прямоугольника, ограниченного началом координат и точкой квадрата, площадь прямоугольника была хорошо аппроксимирована числом точек в нем. ^[2]${\displaystyle n}$

Рот измерил это приближение с помощью квадрата разности между числом точек и умножением на площадь и доказал, что для случайно выбранного прямоугольника ожидаемое значение квадрата разности является логарифмическим по . Этот результат является наилучшим возможным и значительно улучшил предыдущую оценку по той же задаче Татьяны Павловны Эренфест . ^[16] Несмотря на предыдущую работу Эренфеста и Иоганнеса ван дер Корпута по той же задаче, Рот был известен тем, что хвастался, что этот результат «начал тему». ^[2]${\displaystyle n}$${\displaystyle n}$

Некоторые из самых ранних работ Рота включают статью 1949 года о суммах степеней , показывающую, что почти все положительные целые числа могут быть представлены в виде суммы квадрата, куба и четвертой степени, и статью 1951 года о промежутках между числами, свободными от квадратов , которую Чен и Воган описывают как «весьма сенсационную» и «имеющую большое значение» соответственно. ^[2] Его вступительная лекция в Имперском колледже была посвящена большому решету : ограничению размера множеств целых чисел, из которых были запрещены многие классы конгруэнтности чисел по модулю простых чисел . ^[17] Рот ранее опубликовал статью по этой проблеме в 1965 году.

Другим интересом Рота была задача треугольника Хейльбронна , размещение точек в квадрате, чтобы избежать треугольников малой площади. Его статья 1951 года по этой задаче была первой, доказавшей нетривиальную верхнюю границу для площади, которая может быть достигнута. В конечном итоге он опубликовал четыре статьи по этой задаче, последняя из которых была в 1976 году. ^[18] Рот также добился значительного прогресса в упаковке квадратов в квадрате . Если единичные квадраты упакованы в квадрат очевидным способом, параллельным осям, то для значений , которые чуть меньше целого числа, почти площадь может остаться непокрытой. После того, как Пол Эрдёш и Рональд Грэм доказали, что более умная наклонная упаковка может оставить значительно меньшую площадь, только , ^[19] Рот и Боб Воган ответили статьей 1978 года, доказав первую нетривиальную нижнюю границу для этой задачи. Как они показали, для некоторых значений , непокрытая площадь должна быть по крайней мере пропорциональна . [ ^{2] [20]}${\displaystyle s\times s}$${\displaystyle с}$${\displaystyle 2с}$${\displaystyle O(с^{7/11})}$${\displaystyle с}$${\displaystyle {\sqrt {s}}}$

В 1966 году Хайни Халберстам и Рот опубликовали свою книгу Sequences , посвященную целочисленным последовательностям . Первоначально планировалось, что она станет первой из двухтомного издания, ее темы включали плотности сумм последовательностей, границы числа представлений целых чисел в виде сумм членов последовательностей, плотность последовательностей, суммы которых представляют все целые числа, теорию решета и вероятностный метод , а также последовательности, в которых ни один элемент не является кратным другому . ^[21] Второе издание было опубликовано в 1983 году. ^[22]

Рот получил медаль Филдса в 1958 году за свою работу по диофантовым приближениям. Он был первым британским обладателем медали Филдса. ^[1] Он был избран в Королевское общество в 1960 году, а позже стал почетным членом Королевского общества Эдинбурга , членом Лондонского университетского колледжа, членом Лондонского имперского колледжа и почетным членом Питерхауса. ^[1] Для него было источником забавы то, что его медаль Филдса, избрание в Королевское общество и профессорская кафедра пришли к нему в обратном порядке их престижа. ^[2]

В 1983 году Лондонское математическое общество наградило Рота медалью Де Моргана. ^[3] В 1991 году Королевское общество наградило его медалью Сильвестра «за его многочисленный вклад в теорию чисел и, в частности, за решение знаменитой задачи, касающейся приближения алгебраических чисел рациональными числами». ^[23]

В 2009 году в честь 80-летия Рота был опубликован сборник из 32 эссе по темам, связанным с исследованиями Рота, ^[24], а в 2017 году редакторы журнала Mathematika Лондонского университетского колледжа посвятили Роту специальный выпуск. ^[25] После смерти Рота математический факультет Имперского колледжа учредил стипендию Рота в его честь. ^[26]

• Рот, К.Ф. (1949). «Доказательство того, что почти все положительные целые числа являются суммами квадрата, положительного куба и четвертой степени». Журнал Лондонского математического общества . Вторая серия. 24 : 4–13. doi :10.1112/jlms/s1-24.1.4. MR  0028336. Zbl  0032.01401.
• Рот, К. Ф. (1951a). «О проблеме Хейльбронна». Журнал Лондонского математического общества . Вторая серия. 26 (3): 198–204. doi :10.1112/jlms/s1-26.3.198. MR  0041889. Zbl  0043.16303.
• Рот, К. Ф. (1951б). «О промежутках между числами, свободными от квадратов». Журнал Лондонского математического общества . Вторая серия. 26 (4): 263–268. doi :10.1112/jlms/s1-26.4.263. MR  0043119. Zbl  0043.04802.
• Рот, К. Ф. (1953). «О некоторых множествах целых чисел». Журнал Лондонского математического общества . Вторая серия. 28 : 104–109. doi :10.1112/jlms/s1-28.1.104. MR  0051853. Zbl  0050.04002.
• Рот, К. Ф. (1954). «О нерегулярностях распределения». Mathematika . 1 (2): 73–79. doi :10.1112/S0025579300000541. MR  0066435. Zbl  0057.28604.
• Рот, К. Ф. (1955). «Рациональные приближения к алгебраическим числам». Mathematika . 2 : 1–20, 168. doi :10.1112/S0025579300000644. MR  0072182. Zbl  0064.28501.
• Рот, КФ (1965). «О больших решетах Линника и Реньи». Mathematika . 12 : 1–9. doi :10.1112/S0025579300005088. MR  0197424. Zbl  0137.25904.
• Рот, К. Ф. (1976). «Развитие проблемы треугольника Хейльбронна». Advances in Mathematics . 22 (3): 364–385. doi : 10.1016/0001-8708(76)90100-6 . MR  0429761. Zbl  0338.52005.
• Рот, К. Ф.; Воган, Р. К. (1978). «Неэффективность упаковки квадратов единичными квадратами». Журнал комбинаторной теории . Серия A. 24 (2): 170–186. doi : 10.1016/0097-3165(78)90005-5 . MR  0487806. Zbl  0373.05026.

• Хальберштам, Хейни ; Рот, Клаус Фридрих (1966). Последовательности . Лондон: Кларендон Пресс.^[21] Второе издание было опубликовано в 1983 году издательством Springer-Verlag . ^[22]