Квадратная мозаика Тетракис
| Квадратная мозаика Тетракис | |
|---|---|
 | |
| Тип | Двойная полуправильная мозаика |
| Лица | треугольник 45-45-90 |
| Диаграмма Коксетера |           |
| Группа симметрии | п4м, [4,4], *442 |
| Группа вращения | р4, [4,4] + , (442) |
| Двойной многогранник | Усеченная квадратная мозаика |
| Конфигурация лица | В4.8.8 |
| Характеристики | фейс-транзитивный |
В геометрии мозаика тетракис -квадрат — это мозаика евклидовой плоскости . Это квадратная мозаика , в которой каждый квадрат разделен на четыре равнобедренных прямоугольных треугольника из центральной точки, образуя бесконечное множество линий . Ее также можно сформировать, разделив каждый квадрат сетки на два треугольника диагональю, причем диагонали чередуются по направлению, или наложив две квадратные сетки, одну повернутой на 45 градусов относительно другой и масштабированной с коэффициентом √2 .
Конвей , Бергиль и Гудман-Штраус называют его kisquadrille , [1] представленным операцией kis , которая добавляет центральную точку и треугольники для замены граней квадратной мозаики (кадриль). Его также называют решеткой Union Jack из-за сходства с флагом Великобритании треугольников, окружающих его вершины степени 8. [2]
Он обозначен как V4.8.8, поскольку каждая грань равнобедренного треугольника имеет два типа вершин: одну с 4 треугольниками и две с 8 треугольниками.
Как двойная однородная мозаика
Это двойная мозаика усеченной квадратной мозаики , которая имеет один квадрат и два восьмиугольника в каждой вершине. [3]
Приложения
Часть квадратной мозаики тетракис размером 5 × 9 используется для формирования доски для малагасийской настольной игры Fanorona . В этой игре фигуры размещаются на вершинах мозаики и перемещаются вдоль краев, захватывая фигуры другого цвета до тех пор, пока одна из сторон не захватит все фигуры другой стороны. В этой игре вершины степени 4 и степени 8 мозаики называются соответственно слабыми пересечениями и сильными пересечениями, различие, которое играет важную роль в стратегии игры. [4] Похожая доска также используется для бразильской игры Adugo и для игры Hare and Hounds .
Квадратная мозаика тетракис использовалась для набора памятных почтовых марок, выпущенных Почтовой службой США в 1997 году, с чередующимся рисунком из двух разных марок. По сравнению с более простым рисунком для треугольных марок, в которых все диагональные перфорации параллельны друг другу, рисунок тетракис имеет то преимущество, что при сгибании вдоль любой из его перфораций другие перфорации выстраиваются в линию друг с другом, что делает возможным повторное складывание. [5]
Эта мозаика также является основой для широко используемых в стегании узоров «вертушка», «мельница» и «битая посуда» . [6] [7] [8]
Симметрия
Тип симметрии:
- с раскраской: cmm; примитивная ячейка — 8 треугольников, фундаментальная область — 2 треугольника (по 1/2 каждого цвета)
- с темными треугольниками черного цвета и светлыми треугольниками белого цвета: p4g; примитивная ячейка — это 8 треугольников, фундаментальная область — 1 треугольник (по 1/2 для черного и белого цвета)
- с черными краями и белыми внутренностями: p4m; примитивная ячейка — это 2 треугольника, фундаментальная область — 1/2
Края мозаики тетракис-квадрат образуют симплициальное расположение линий — свойство, которое она разделяет с треугольной мозаикой и мозаикой кисромбилл .
Эти линии образуют оси симметрии группы отражений ( группа обоев [4,4], (*442) или p4m), которая имеет треугольники мозаики в качестве своих фундаментальных областей . Эта группа изоморфна , но не совпадает с группой автоморфизмов мозаики, которая имеет дополнительные оси симметрии, делящие треугольники пополам, и которая имеет полутреугольники в качестве своих фундаментальных областей.
Существует множество небольших индексных подгрупп симметрии p4m, [4,4] (*442 орбифолдная нотация ), которые можно увидеть в отношении диаграммы Коксетера , с узлами, окрашенными в соответствии с линиями отражения, и точками инерции, помеченными численно. Вращательная симметрия показана попеременно белыми и синими областями с одним фундаментальным доменом для каждой подгруппы, заполненным желтым цветом. Скользящие отражения показаны пунктирными линиями.
Подгруппы могут быть выражены в виде диаграмм Кокстера , а также фундаментальных диаграмм доменов.
| Малые индексные подгруппы p4m, [4,4], (*442) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| индекс | 1 | 2 | 4 | ||||||||
| Фундаментальная диаграмма домена |  |  |  |  |  |  | |||||
| Обозначение Коксетера Диаграмма Коксетера | [ 1 ,4, 1 ,4, 1 ] = [4,4]     | [1 + ,4,4]     = =   | [4,4,1 + ]     = =   | [4,1 + ,4]     = =   | [1 + ,4,4,1 + ]     = =     | [4 + ,4 + ] = [(4,4 + ,2 + )]     | |||||
| Орбифолд | *442 | *2222 | 22× | ||||||||
| Полупрямые подгруппы | |||||||||||
| индекс | 2 | 4 | |||||||||
| Диаграмма |  |  |  |  |  | ||||||
| Коксетер | [4,4 + ]     | [4 + ,4]     | [(4,4,2 + )]    | [1 + ,4,1 + ,4]=[(2 + ,4,4)]     = =    = =    | [4,1 + ,4,1 + ]=[(4,4,2 + )]     = =    = =    | ||||||
| Орбифолд | 4*2 | 2*22 | |||||||||
| Прямые подгруппы | |||||||||||
| Индекс | 2 | 4 | 8 | ||||||||
| Диаграмма | 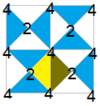 |  |  |  |  | ||||||
| Коксетер | [4,4] +    | [1 + ,4,4 + ] = [4,4 + ] +     = =    | [4 + ,4,1 + ] = [4 + ,4] +     = =    | [(4,1 + ,4,2 + )] = [(4,4,2 + )] +     = =     | [1 + ,4,1 + ,4,1 + ] = [(4 + ,4 + ,2 + )] = [4 + ,4 + ] +     = =      | ||||||
| Орбифолд | 442 | 2222 | |||||||||
Смотрите также
Примечания
- ^ Конвей, Джон ; Берджил, Хайди; Гудман-Штраус, Хаим (2008), «Глава 21: Наименование архимедовых и каталонских многогранников и мозаик», Симметрии вещей , AK Peters, стр. 288, ISBN 978-1-56881-220-5
- ^ Стивенсон, Джон, «Модель Изинга с антиферромагнитной связью следующего ближайшего соседа: спиновые корреляции и точки беспорядка», Phys. Rev. B , 1 (11): 4405– 4409, doi :10.1103/PhysRevB.1.4405.
- ^ Вайсштейн, Эрик В. «Двойная тесселяция». MathWorld .
- ^ Белл, RC (1983), «Фанорона», The Boardgame Book , Exeter Books, стр. 150–151 , ISBN 0-671-06030-9
- ^ Фредериксон, Грег Н. (2006), Piano-Hinged Dissections , AK Peters, стр. 144.
- ^ Библия квилтинга, Creative Publishing International, 1997, стр. 55, ISBN 9780865732001.
- ^ Зиман, Нэнси (2011), Quilt With Confidence, Krause Publications, стр. 66, ISBN 9781440223556.
- ^ Фассетт, Каффе (2007), Калейдоскоп лоскутных одеял Каффе Фассетт: двадцать дизайнов от Роуэна для пэчворка и квилтинга, Taunton Press, стр. 96, ISBN 9781561589388.
Ссылки
- Грюнбаум, Бранко и Шепард, GC (1987). Tilings and Patterns . Нью-Йорк: WH Freeman. ISBN 0-7167-1193-1.(Глава 2.1: Правильные и однородные мозаики , стр. 58-65)
- Уильямс, Роберт (1979). Геометрическая основа естественной структуры: путеводитель по дизайну . Dover Publications, Inc. стр. 40. ISBN 0-486-23729-X.
- Кейт Кричлоу, «Порядок в пространстве: справочник по дизайну» , 1970, стр. 77-76, образец 8

