Икосододекаэдр

Икосододекаэдр
Тип	Архимедово тело Однородный многогранник Квазиправильный многогранник
Лица	32
Края	60
Вершины	30
Группа симметрии	Икосаэдрическая симметрия I h
Двугранный угол ( градусы )	142.62°
Двойной многогранник	Ромбический триаконтаэдр
Характеристики	выпуклый
Вершинная фигура
Сеть

В геометрии икосододекаэдр или пентагональная гиробиротунда — многогранник с двадцатью ( икоси- ) треугольными гранями и двенадцатью ( додека- ) пятиугольными гранями. Икосододекаэдр имеет 30 одинаковых вершин , в каждой из которых сходятся два треугольника и два пятиугольника, и 60 одинаковых рёбер, каждое из которых отделяет треугольник от пятиугольника. Таким образом, он является одним из архимедовых тел и, в частности, квазиправильным многогранником .

Один из способов построить икосододекаэдр — начать с двух пятиугольных ротонд , прикрепив их к своим основаниям. Эти ротонды покрывают свое десятиугольное основание, так что полученный многогранник имеет 32 грани, 30 вершин и 60 ребер. Эта конструкция похожа на одно из тел Джонсона , пятиугольную ортобиротонду . Разница в том, что икосододекаэдр построен путем скручивания его ротонд на 36°, процесс, известный как гирация , в результате чего пятиугольная грань соединяется с треугольной. У икосододекаэдра есть альтернативное название, пятиугольная гиробиротонда . ^{[1] [2]}

Удобные декартовы координаты для вершин икосододекаэдра с единичными ребрами задаются четными перестановками : где φ обозначает золотое сечение . ^[3]$${\displaystyle (0,0,\pm \varphi ),\qquad \left(\pm {\frac {1}{2}},\pm {\frac {\varphi }{2}},\pm {\frac {\varphi ^{2}}{2}}\right),}$$

Площадь поверхности икосододекаэдра A можно определить, вычислив площадь всех пятиугольных граней. Объем икосододекаэдра V можно определить, разрезав его на две пятиугольные ротонды, после чего суммировав их объемы. Таким образом, его площадь поверхности и объем можно сформулировать как: ^[1]$${\displaystyle {\begin{aligned}A&=\left(5{\sqrt {3}}+3{\sqrt {25+10{\sqrt {5}}}}\right)a^{2}&\approx 29.306a^{2}\\V&={\frac {45+17{\sqrt {5}}}{6}}a^{3}&\approx 13.836a^{3}.\end{aligned}}}$$

Двугранный угол икосододекаэдра между пятиугольником и треугольником определяется путем вычисления угла пятиугольной ротонды. ^[4]$${\displaystyle \arccos \left(-{\sqrt {\frac {5+2{\sqrt {5}}}{15}}}\right)\approx 142.62^{\circ },}$$

Икосододекаэдр имеет икосаэдрическую симметрию , а его первая звёздчатая форма представляет собой соединение додекаэдра и его двойственного икосаэдра , причём вершины икосододекаэдра расположены в серединах рёбер каждого из них.

Икосододекаэдр является архимедовым телом , то есть это высокосимметричный и полуправильный многогранник, и две или более различных правильных многоугольных граней сходятся в вершине. ^[5] Многоугольные грани, которые сходятся для каждой вершины, — это два равносторонних треугольника и два правильных пятиугольника, а вершинная фигура икосододекаэдра — это {{nowrap|(3·5) ² = 3 ² ·5 ² }. Его двойственный многогранник — ромбический триаконтаэдр , каталонское тело . ^[4]

Икосододекаэдр имеет 6 центральных декагонов . Спроецированные на сферу, они определяют 6 больших окружностей . Фуллер (1975) использовал эти 6 больших окружностей, а также 15 и 10 других в двух других многогранниках, чтобы определить свои 31 большую окружность сферического икосаэдра . ^[6]

Длинный радиус (от центра до вершины) икосододекаэдра находится в золотом соотношении к длине его ребра; таким образом, его радиус равен φ, если длина его ребра равна 1, а длина его ребра равна ⁠1/φ⁠ если его радиус равен 1. ^[4] Только несколько однородных многогранников обладают этим свойством, включая четырехмерный 600-ячейник , трехмерный икосододекаэдр и двумерный декагон . (Икосододекаэдр является экваториальным сечением 600-ячейника, а декагон является экваториальным сечением икосододекаэдра.) Эти радиально золотые многогранники могут быть построены с их радиусами из золотых треугольников , которые встречаются в центре, каждый из которых вносит два радиуса и ребро.

Икосододекаэдр — это спрямленный додекаэдр , а также спрямленный икосаэдр , существующий как полное усечение между этими правильными телами.

Икосододекаэдр содержит 12 пятиугольников додекаэдра и 20 треугольников икосаэдра :

Семейство однородных икосаэдрических многогранников
Симметрия : [5,3] , (*532)							[5,3] + , (532)
{5,3}	т{5,3}	г{5,3}	т{3,5}	{3,5}	рр{5,3}	тр{5,3}	ср{5,3}
Двойственные к однородным многогранникам
В5.5.5	В3.10.10	В3.5.3.5	В5.6.6	В3.3.3.3.3	В3.4.5.4	В4.6.10	В3.3.3.3.5

Икосододекаэдр существует в последовательности симметрий квазиправильных многогранников и мозаик с конфигурациями вершин (3. n ) ² , прогрессирующих от мозаик сферы до евклидовой плоскости и в гиперболическую плоскость. С симметрией орбифолдной нотации * n 32 все эти мозаики являются wythoff конструкцией в фундаментальной области симметрии с точками генератора в прямоугольном углу области. ^{[7] [8]}

* n 32 орбифолдных симметрий квазирегулярных мозаик : (3. n ) 2
Строительство	Сферический			Евклидов	Гиперболический
	*332	*432	*532	*632	*732	*832...	*∞32
Квазирегулярные фигуры
Вершина	(3.3) 2	(3.4) 2	(3.5)2	(3,6) 2	(3,7) 2	(3,8) 2	(3.∞) 2

*5 n 2 мутаций симметрии квазирегулярных мозаик: (5. n ) 2 в т е
Симметрия *5 n 2 [n,5]	Сферический	Гиперболический					Паракомпактный	Некомпактный
	*352 [3,5]	*452 [4,5]	*552 [5,5]	*652 [6,5]	*752 [7,5]	*852 [8,5]...	*∞52 [∞,5]	[ н я,5]
Цифры
Конфигурация.	(5.3)2	(5.4) 2	(5,5) 2	(5.6) 2	(5.7)2	(5.8)2	(5.∞) 2	(5. н я) 2
Ромбовидные фигуры
Конфигурация.	В(5.3) 2	В(5.4) 2	В(5,5) 2	В(5,6) 2	В(5,7) 2	В(5,8) 2	V(5.∞) 2	V(5.∞) 2

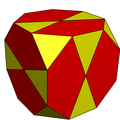
Усеченный куб можно превратить в икосододекаэдр, разделив восьмиугольники на два пятиугольника и два треугольника. Он имеет пиритоэдрическую симметрию .

Восемь однородных звездчатых многогранников имеют одинаковое расположение вершин . Из них два также имеют одинаковое расположение ребер : малый икосигемидодекаэдр (имеющий общие треугольные грани) и малый додекахемидодекаэдр (имеющий общие пятиугольные грани). Расположение вершин также является общим для соединений пяти октаэдров и пяти тетрагемигексаэдров .

Икосододекаэдр	Малый икосигемидодекаэдр	Малый додекагемидодекаэдр
Большой икосододекаэдр	Большой додекагемидодекаэдр	Большой икосигемидодекаэдр
Додекадодекаэдр	Малый додекагемикосаэдр	Большой додекагемикосаэдр
Соединение пяти октаэдров	Соединение пяти тетрагемигексаэдров

В четырехмерной геометрии икосододекаэдр появляется в правильной 600-ячейке как экваториальный срез, который принадлежит вершинно-первому проходу 600-ячейки через трехмерное пространство. Другими словами: 30 вершин 600-ячейки, которые лежат на дуговых расстояниях 90 градусов на ее описанной гиперсфере от пары противоположных вершин, являются вершинами икосододекаэдра. Каркасная фигура 600-ячейки состоит из 72 плоских правильных декагонов. Шесть из них являются экваториальными декагонами к паре противоположных вершин, и эти шесть образуют каркасную фигуру икосододекаэдра.

Если 600-ячейковый многогранник стереографически спроецировать в 3-мерное пространство относительно любой вершины и все точки нормализовать, то геодезические, на которые падают ребра, составят барицентрическое подразделение икосододекаэдра .

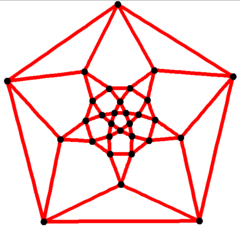
Скелет икосододекаэдра можно представить как граф с 30 вершинами и 60 ребрами, один из архимедовых графов . Он является квартикальным , что означает, что каждая его вершина соединена с четырьмя другими вершинами. ^[9]

Икосододекаэдр может встречаться в таких структурах, как геодезический купол или сфера Хобермана .

Икосододекаэдры можно обнаружить во всех эукариотических клетках, включая клетки человека, в виде образований белков оболочки Sec13/31 COPII . ^[10]

Икосододекаэдр также может встречаться в популярной культуре. Во вселенной Star Trek , вулканская логическая игра Kal-Toh имеет целью создание формы с двумя вложенными голографическими икосододекаэдрами, соединенными в серединах их сегментов.

• Кубооктаэдр
• Большой усеченный икосододекаэдр
• Икосаэдр
• Ромбокосододекаэдр
• Усеченный икосододекаэдр

• Кромвель, П. (1997). Многогранники . Великобритания: Кембридж. стр. 79–86 Архимедовы тела . ISBN 0-521-55432-2.

• Вайсштейн, Эрик В. , «Икосододекаэдр» («Архимедово тело») на MathWorld .
• Клитцинг, Ричард. «Трехмерные выпуклые однородные многогранники o3x5o - id».
• Редактируемая печатная развертка икосододекаэдра с интерактивным 3D-просмотром
• Однородные многогранники
• Виртуальная реальность Многогранники Энциклопедия многогранников