Соединение пяти октаэдров

Соединение пяти октаэдров
(см. здесь 3D-модель)
Тип	Регулярное соединение
Индекс	УК 17 , Ж 23
символ Коксетера	[5{3,4}]2{3,5} [1]
Элементы (в составе)	5 октаэдров : F = 40, E = 60, V = 30
Двойной состав	Соединение пяти кубов
Группа симметрии	икосаэдрический ( I h )
Подгруппа, ограничивающаяся одним компонентом	пиритоэдрический ( T h )

Соединение пяти октаэдров является одним из пяти правильных многогранных соединений , и его также можно рассматривать как звёздчатое образование . Впервые оно было описано Эдмундом Гессом в 1876 году. Оно уникально среди правильных соединений тем, что не имеет правильной выпуклой оболочки.

Это вторая звёздчатая форма икосаэдра , имеющая индекс модели Веннингера 23 .

Его можно построить с помощью ромбического триаконтаэдра с пирамидами на ромбических основаниях , добавленными ко всем граням, как показано на пятицветном изображении модели. (Эта конструкция не создает правильное соединение пяти октаэдров, но имеет ту же топологию и может быть плавно деформирована в правильное соединение.)

Плотность больше 1.

Диаграмма звездчатости	Ядро звездчатой ​​формы	Выпуклая оболочка
	Икосаэдр	Икосододекаэдр

Его также можно рассматривать как полиэдрическое соединение пяти октаэдров, расположенных в икосаэдрической симметрии ( I _h ).

Сферические и стереографические проекции этого соединения выглядят так же , как у дисдьякистриаконтаэдра . Но вершины выпуклого тела на осях симметрии 3-го и 5-го порядка (серые на изображениях ниже) соответствуют только пересечениям ребер в соединении.

Сферический многогранник	Стереографические проекции
	2-кратный	3-кратный	5-кратный
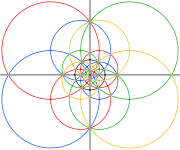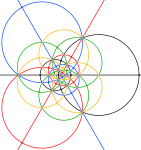Область в черных кругах ниже соответствует фронтальной полусфере сферического многогранника.

Замена октаэдров тетрагемигексаэдрами приводит к соединению пяти тетрагемигексаэдров .

Существует также второе соединение из 5 октаэдров с октаэдрической симметрией. Его можно получить, добавив пятый октаэдр к стандартному соединению из 4 октаэдров .

• Соединение трех октаэдров
• Соединение четырех октаэдров
• Соединение десяти октаэдров
• Соединение двадцати октаэдров

• Питер Р. Кромвель, Многогранники , Кембридж, 1997.
• Веннингер, Магнус (1974). Модели многогранников . Cambridge University Press. ISBN 0-521-09859-9.
• Коксетер, Гарольд Скотт Макдональд ; Дю Валь, П.; Флатер, Х.Т.; Петри, Дж.Ф. (1999). Пятьдесят девять икосаэдров (3-е изд.). Тарквиний. ISBN 978-1-899618-32-3. МР  0676126.(1-й Эдн Университет Торонто (1938))
• HSM Coxeter , Regular Polytopes , (3-е издание, 1973), издание Dover, ISBN 0-486-61480-8 , 3.6 Пять правильных соединений , стр. 47-50, 6.2 Формирование звездчатых форм Платоновых тел , стр. 96-104 
• Э. Гесс 1876 Zugleich Gleicheckigen und Gleichflächigen Polyeder , Schriften der Gesellschaft zur Berörderung der Gasammten Naturwissenschaften zu Marburg 11 (1876), стр. 5–97.

• MathWorld: Октаэдр5-Соединение
• Бумажная модель соединения пяти октаэдров
• Клитцинг, Ричард. «3D-соединение».
• Октаэдр-5-соединение как пентаграмма Гаусса Мирификум

Известные звёздчатые формы икосаэдра
Обычный	Равномерные дуалы			Регулярные соединения			Обычная звезда	Другие
(Выпуклый) икосаэдр	Малый триамбический икосаэдр	Медиальный триамбический икосаэдр	Большой триамбический икосаэдр	Соединение пяти октаэдров	Соединение пяти тетраэдров	Соединение десяти тетраэдров	Большой икосаэдр	Выкопанный додекаэдр	Окончательная звездчатость
Процесс образования звездчатой ​​формы на икосаэдре создает ряд родственных многогранников и соединений с икосаэдрической симметрией .

Эта статья о многогранниках — заглушка . Вы можете помочь Википедии, расширив ее.

• в
• т
• е