Шестнадцатеричный
| Часть серии статей о |
| Системы счисления |
|---|
| Список систем счисления |
Шестнадцатеричная (также известная как base-16 или просто hex ) — это позиционная система счисления , которая представляет числа с использованием основания (основания) шестнадцать. В отличие от десятичной системы, представляющей числа с использованием десяти символов, шестнадцатеричная использует шестнадцать различных символов, чаще всего символы «0»–«9» для представления значений от 0 до 9 и «A»–«F» для представления значений от десяти до пятнадцати.
Разработчики программного обеспечения и проектировщики систем широко используют шестнадцатеричные числа, поскольку они обеспечивают удобное представление двоично-кодированных значений. Каждая шестнадцатеричная цифра представляет четыре бита (двоичные цифры), также известные как полубайт (или ниббл). [1] Например, 6-битный байт может иметь значения в диапазоне от 000000 до 111111 (от 0 до 63 в десятичной системе) в двоичной форме, что может быть записано как от 00 до 3F в шестнадцатеричной системе.
В математике нижний индекс обычно используется для указания основания. Например, десятичное значение711 будет выражено в шестнадцатеричном виде как 2C7 16 . В программировании существует несколько обозначений для обозначения шестнадцатеричных чисел, обычно с использованием префикса. Префикс 0xиспользуется в C , который будет обозначать это значение как 0x2C7.
В кодировке Base 16 используется шестнадцатеричная система счисления , в которой каждый байт открытого текста разбивается на два 4-битных значения и представляется двумя шестнадцатеричными цифрами.
Представление
Письменное представление
В большинстве современных вариантов использования буквы A–F или a–f представляют значения 10–15, тогда как цифры 0–9 используются для представления их десятичных значений.
Не существует универсальной конвенции об использовании нижнего или верхнего регистра, поэтому каждый из них распространен или предпочтителен в определенных средах по стандартам или конвенции сообщества; используется даже смешанный регистр. Некоторые семисегментные дисплеи используют смешанный регистр 'A b C d E F', чтобы отличать цифры A–F друг от друга и от 0–9.
Существует некоторая стандартизация использования пробелов (вместо запятых или других знаков препинания) для разделения шестнадцатеричных значений в длинном списке. Например, в следующем шестнадцатеричном дампе каждый 8-битный байт представляет собой 2-значное шестнадцатеричное число с пробелами между ними, в то время как 32-битное смещение в начале представляет собой 8-значное шестнадцатеричное число.
00000000 57 69 6b 69 70 65 64 69 61 2c 20 74 68 65 20 66 00000010 72 65 65 20 65 6e 63 79 63 6c 6f 70 65 64 69 61 00000020 20 74 68 61 74 20 61 6e 79 6f 6e 65 20 63 61 6e 00000030 20 65 64 69 74 0a Отличие от десятичной дроби
В контекстах, где основание не ясно, шестнадцатеричные числа могут быть неоднозначными и путаться с числами, выраженными в других основаниях. Существует несколько соглашений для однозначного выражения значений. Числовой нижний индекс (сам записанный в десятичной системе) может явно указывать основание: 159 10 — это десятичное 159; 159 16 — это шестнадцатеричное 159, что равно 345 10 . Некоторые авторы предпочитают текстовый нижний индекс, например, 159 decimal и 159 hex или 159 d и 159 h .
Дональд Кнут в своей книге The TeXbook представил использование особого шрифта для представления определенного основания системы счисления . [2] Шестнадцатеричные представления записаны там шрифтом пишущей машинки : 5A3 , C1F27ED
В линейных текстовых системах, которые используются в большинстве сред компьютерного программирования, возникло множество методов:
- Хотя префикс для указания шестнадцатеричной константы наиболее известен из языка программирования C (и многих языков, на которые повлиял C), префикс
0xдля указания шестнадцатеричной константы, возможно, возник в системах IBM Stretch . Он произошел от0префикса, уже использовавшегося для восьмеричных констант. Значения байтов могут быть выражены в шестнадцатеричном формате с префиксом,\xза которым следуют две шестнадцатеричные цифры:'\x1B'представляет управляющий символ Esc ;"\x1B[0m\x1B[25;1H"— строка, содержащая 11 символов с двумя встроенными символами Esc. [3] Для вывода целого числа в шестнадцатеричном формате с помощью семейства функций printf используется код преобразования формата%Xили .%x - В XML и XHTML символы могут быть выражены как шестнадцатеричные числовые ссылки на символы с использованием нотации , например, представляет символ U+0054 (заглавная буква «T»). Если нет, число является десятичным (то есть это тот же символ). [4]
ode;TxT - В языках ассемблера, полученных от Intel , и Modula-2 [5] шестнадцатеричное число обозначается суффиксом H или h : или . Некоторые реализации требуют начального нуля, когда первый символ шестнадцатеричной цифры не является десятичной цифрой, поэтому вместо этого следует писать . Некоторые другие реализации (например, NASM) допускают числа в стиле C ( ).
FFh05A3H0FFhFFh0x42 - Другие языки ассемблера ( 6502 , Motorola ), Pascal , Delphi , некоторые версии BASIC ( Commodore ), GameMaker Language , Godot и Forth используют
$в качестве префикса:$5A3,$C1F27ED. - Некоторые языки ассемблера (Microchip) используют обозначение
H'ABCD'(для ABCD 16 ). Аналогично, Fortran 95 использует Z'ABCD'. - Ada и VHDL заключают шестнадцатеричные числа в «числовые кавычки»:
16#5A3#,16#C1F27ED#. Для констант битового вектора VHDL использует обозначениеx"5A3",x"C1F27ED". [6] - Verilog представляет шестнадцатеричные константы в форме
8'hFF, где 8 — количество бит в значении, а FF — шестнадцатеричная константа. - В языках Icon и Smalltalk используется префикс :
16r16r5A3 - PostScript и оболочка Bourne , а также ее производные обозначают шестнадцатеричное число с префиксом
16#:16#5A3,16#C1F27ED. - Common Lisp использует префиксы
#xи#16r. Установка переменных *read-base* [7] и *print-base* [8] на 16 также может использоваться для переключения считывателя и принтера системы Common Lisp на шестнадцатеричное представление чисел для чтения и печати чисел. Таким образом, шестнадцатеричные числа могут быть представлены без кода префикса #x или #16r, когда входная или выходная база была изменена на 16. - MSX BASIC , [9] QuickBASIC , FreeBASIC и Visual Basic добавляют к шестнадцатеричным числам префикс
&H:&H5A3 - BBC BASIC и Locomotive BASIC используют
&для шестнадцатеричного кода. [10] - В сериях TI-89 и 92 используется
0hпрефикс:0h5A3,0hC1F27ED - В АЛГОЛ 68
16rдля обозначения шестнадцатеричных чисел используется префикс :16r5a3,16rC1F27ED. Двоичные, четверичные (основание 4) и восьмеричные числа могут быть заданы аналогичным образом. - Наиболее распространенным форматом для шестнадцатеричного числа на мэйнфреймах IBM ( zSeries ) и компьютерах среднего уровня ( IBM i ) под управлением традиционных ОС ( zOS , zVSE , zVM , TPF , IBM i ) является
X'5A3'илиX'C1F27ED', и он используется в Assembler, PL/I , COBOL , JCL , скриптах, командах и других местах. Этот формат был распространен и на других (и теперь устаревших) системах IBM. Иногда вместо апострофов использовались кавычки.
Синтаксис, который всегда шестнадцатеричный
Иногда известно, что числа имеют шестнадцатеричную систему счисления.
- В URI (включая URL ) коды символов записываются в виде шестнадцатеричных пар с префиксом
%:http://www.example.com/name%20with%20spacesгде%20— код символа пробела (пустого символа) , код ASCII 20 в шестнадцатеричном формате, 32 в десятичном формате. - В стандарте Unicode значение символа представляется с
U+последующим шестнадцатеричным значением, например,U+00A1перевернутым восклицательным знаком (¡). - Ссылки на цвета в HTML, CSS и X Window могут быть выражены шестью шестнадцатеричными цифрами (по две для красного, зеленого и синего компонентов в указанном порядке) с префиксом
#: например, пурпурный цвет#FF00FFпредставляется как . [11] CSS также допускает аббревиатуры из 3 шестнадцатеричных цифр с одной шестнадцатеричной цифрой на компонент:#FA3аббревиатуры#FFAA33(золотисто-оранжевый: ). - В кодировке MIME (расширения электронной почты) quote-printable коды символов записываются в виде шестнадцатеричных пар с префиксом
=:Espa=F1a— это «España» ( шестнадцатеричный код F1 — это код для ñ в наборе символов ISO/IEC 8859-1). [12] ) - Двоичные данные PostScript (например, пиксели изображения ) могут быть выражены в виде последовательных шестнадцатеричных пар без префиксов:
AA213FD51B3801043FBC... - Любой адрес IPv6 можно записать в виде восьми групп по четыре шестнадцатеричных цифры (иногда называемых гекстетами ), где каждая группа отделена двоеточием (
:). Это, например, допустимый адрес IPv6:2001:0db8:85a3:0000:0000:8a2e:0370:7334или сокращенно путем удаления начальных нулей как2001:db8:85a3::8a2e:370:7334( Адреса IPv4 обычно записываются в десятичном виде). - Глобально уникальные идентификаторы записываются в виде тридцати двух шестнадцатеричных цифр, часто в неравных группах, разделенных дефисом, например
3F2504E0-4F89-41D3-9A0C-0305E82C3301.
Другие символы для 10–15 и в основном другие наборы символов
Использование букв от A до F для обозначения цифр выше 9 не было общепринятым на раннем этапе развития компьютеров.
- В 1950-х годах в некоторых установках, таких как Bendix-14, предпочитали использовать цифры от 0 до 5 с чертой сверху для обозначения значений 10–15 как 0 , 1 , 2 , 3 , 4 и 5 .
- Компьютеры SWAC ( 1950) [13] и Bendix G-15 (1956) [14] [13] использовали строчные буквы u , v , w , x , y и z для значений от 10 до 15.
- Компьютеры ORDVAC и ILLIAC I (1952) (и некоторые производные конструкции, например BRLESC ) использовали заглавные буквы K , S , N , J , F и L для значений от 10 до 15. [15] [13]
- Librascope LGP-30 (1956) использовал буквы F , G , J , K , Q и W для значений от 10 до 15. [16] [13]
- На компьютере PERM (1956) шестнадцатеричные числа записывались буквами O для нуля, A до N и P для чисел от 1 до 15. Многие машинные инструкции имели мнемонические шестнадцатеричные коды ( A = сложение, M = умножение, L = загрузка, F = с фиксированной точкой и т. д.); программы писались без названий инструкций. [17]
- В Honeywell Datamatic D-1000 (1957) использовались строчные буквы b , c , d , e , f и g, тогда как в Elbit 100 (1967) использовались заглавные буквы B , C , D , E , F и G для значений от 10 до 15. [13]
- Monrobot XI (1960) использовал буквы S , T , U , V , W и X для значений от 10 до 15. [13]
- Параметронный компьютер NEC NEAC 1103 (1960) использовал буквы D , G , H , J , K (и, возможно, V ) для значений 10–15. [18]
- В Pacific Data Systems 1020 (1964) для значений от 10 до 15 использовались буквы L , C , A , S , M и D. [13]

- Новые числовые символы и названия были введены в биби-бинарную систему счисления Боби Лапуэнтом в 1968 году.
- Брюс Алан Мартин из Брукхейвенской национальной лаборатории посчитал выбор A–F «смешным». В письме редактору CACM от 1968 года он предложил совершенно новый набор символов, основанный на расположении битов. [19]

- В 1972 году Рональд О. Уитакер из Rowco Engineering Co. предложил треугольный шрифт, который допускает «прямое двоичное чтение», чтобы «разрешить как ввод, так и вывод с компьютеров без учета матриц кодирования». [20] [21]
- Некоторые микросхемы декодера семисегментного дисплея (например, 74LS47) показывают неожиданный вывод из-за логики, разработанной для правильного отображения только цифр от 0 до 9. [22]
Вербальные и цифровые представления
Поскольку не было традиционных цифр для представления количеств от десяти до пятнадцати, в качестве замены были повторно использованы буквы алфавита. В большинстве европейских языков отсутствуют слова, не основанные на десятичной системе, для некоторых цифр от одиннадцати до пятнадцати. Некоторые люди читают шестнадцатеричные числа цифра за цифрой, как номер телефона, или используют фонетический алфавит НАТО , фонетический алфавит армии/флота или подобную специальную систему . После принятия шестнадцатеричной системы среди программистов IBM System/360 , Магнусон (1968) [23] предложил руководство по произношению, которое давало короткие названия буквам шестнадцатеричной системы — например, «A» произносилось как «ann», B — как «bet», C — как «chris» и т. д. [23] Другая система наименований была опубликована в Интернете Роджерсом (2007) [24] , который пытается сделать словесное представление различимым в любом случае, даже если фактическое число не содержит цифр A–F. Примеры приведены в таблицах ниже. Еще одна система именования была разработана Баббом (2015) на основе шутки из Кремниевой долины . [25]
Другие предложили использовать словесные соглашения азбуки Морзе для выражения четырехбитных шестнадцатеричных цифр, где «точка» и «тире» представляют ноль и единицу соответственно, так что «0000» озвучивается как «дит-дит-дит-дит» (....), да-дит-дит-да (-..-) озвучивает цифру со значением девять, а «да-да-да-да» (----) озвучивает шестнадцатеричную цифру для десятичного числа 15.

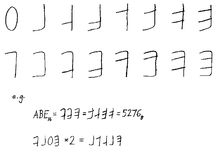
Системы счета по цифрам были разработаны как для двоичной, так и для шестнадцатеричной системы. Артур Кларк предложил использовать каждый палец как бит включения/выключения, что позволило вести счет от нуля до 1023 10 на десяти пальцах. [26] Другая система счета до FF 16 (255 10 ) проиллюстрирована справа.
| Число | Произношение |
|---|---|
| А | энн |
| Б | ставка |
| С | Крис |
| Д | точка |
| Э | Эрнест |
| Ф | мороз |
| 1А | annteen |
| А0 | энти |
| 5Б | пятьдесят-ставка |
| А01С | Энти Кристен |
| 1AD0 | annteen dotty |
| 3А7Д | тридцать-энн семьдесят-точка |
| Число | Произношение |
|---|---|
| А | десять |
| Б | одиннадцать |
| С | двенадцать |
| Д | драже |
| Э | ептин |
| Ф | фильм |
| 10 | текс |
| 11 | одиночек |
| 1 этаж | фимтик |
| 50 | фифтек |
| С0 | твелфтек |
| 100 | хундрек |
| 1000 | тысячасек |
| 3Е | тиртек-ептин |
| Е1 | eptek-один |
| С4А | двенадцать-сто-четыре-десять |
| 1743 | один-двасек-семь- -стосек-четыресек-три |
Знаки
Шестнадцатеричная система может выражать отрицательные числа так же, как и десятичная: −2A для представления −42 10 , −B01D9 для представления −721369 10 и так далее.
Шестнадцатеричное число также может использоваться для выражения точных битовых шаблонов, используемых в процессоре , поэтому последовательность шестнадцатеричных цифр может представлять знаковое или даже плавающее значение. Таким образом, отрицательное число −42 10 может быть записано как FFFF FFD6 в 32-битном регистре ЦП (в дополнительном коде ), как C228 0000 в 32-битном регистре FPU или C045 0000 0000 0000 в 64-битном регистре FPU (в стандарте IEEE с плавающей точкой ).
Шестнадцатеричная экспоненциальная запись
Так же, как десятичные числа могут быть представлены в экспоненциальной нотации , так же могут быть представлены и шестнадцатеричные числа. В нотации P используется буква P (или p , для «степени»), тогда как E (или e ) служит для той же цели в десятичной нотации E . Число после P является десятичным и представляет собой двоичную экспоненту. Увеличение экспоненты на 1 умножает на 2, а не на 16: 20p0 = 10p1 = 8p2 = 4p3 = 2p4 = 1p5 . Обычно число нормализуется таким образом, что шестнадцатеричные цифры начинаются с 1. (ноль обычно равен 0 без P ).
Пример: 1.3DEp42 представляет 1.3DE 16 × 2 42 10 .
Нотация P требуется двоичным стандартом с плавающей точкой IEEE 754-2008 и может использоваться для литералов с плавающей точкой в редакции C99 языка программирования C. [ 27] Используя спецификаторы преобразования %a или %A , эта нотация может быть получена реализациями семейства функций printf , следующих спецификации C99 [28] и стандарту Single Unix Specification (IEEE Std 1003.1) POSIX . [29]
Конверсия
Двоичное преобразование
.jpg/440px-Hewlett-Packard_Model_HP-16C_Programmable_RPN_Calculator,_HP's_First_and_Only_Calculator_esp._for_Programmers,_built_1982-1989_(edited_to_rectangular,_V2).jpg)
Большинство компьютеров оперируют двоичными данными, но людям сложно работать с большим количеством цифр даже для относительно небольшого двоичного числа. Хотя большинство людей знакомы с десятичной системой, гораздо проще преобразовать двоичную систему в шестнадцатеричную, чем в десятичную, поскольку каждая шестнадцатеричная цифра преобразуется в целое число бит (4 10 ). В этом примере число 1111 2 преобразуется в десятичную систему. Поскольку каждая позиция в двоичной системе может содержать либо 1, либо 0, ее значение можно легко определить по ее положению справа:
- 0001 2 = 1 10
- 0010 2 = 2 10
- 0100 2 = 4 10
- 1000 2 = 8 10
Поэтому:
| 1111 2 | = 8 10 + 4 10 + 2 10 + 1 10 |
| = 15 10 |
При небольшой практике преобразование 1111 2 в F 16 за один шаг становится простым (см. таблицу в письменном виде). Преимущество использования шестнадцатеричной системы вместо десятичной быстро увеличивается с размером числа. Когда число становится большим, преобразование в десятичную систему становится очень утомительным. Однако при преобразовании в шестнадцатеричную систему тривиально рассматривать двоичную строку как 4-значные группы и преобразовывать каждую в одну шестнадцатеричную цифру. [30]
В этом примере показано преобразование двоичного числа в десятичное, сопоставление каждой цифры с десятичным значением и сложение результатов.
| (1001011100) 2 | = 512 10 + 64 10 + 16 10 + 8 10 + 4 10 |
| = 604 10 |
Сравните это с преобразованием в шестнадцатеричную систему счисления, где каждая группа из четырех цифр может рассматриваться независимо и преобразовываться напрямую:
| (1001011100) 2 | = | 0010 | 0101 | 1100 2 | ||
| = | 2 | 5 | С 16 | |||
| = | 25С 16 | |||||
Преобразование из шестнадцатеричной системы в двоичную также осуществляется напрямую. [30]
Другие простые преобразования
Хотя четверичная система счисления (основание 4) используется мало, ее можно легко преобразовать в шестнадцатеричную или двоичную систему счисления и обратно. Каждая шестнадцатеричная цифра соответствует паре четверичных цифр, а каждая четверичная цифра соответствует паре двоичных цифр. В приведенном выше примере 2 5 C 16 = 02 11 30 4 .
Восьмеричная (основание 8) система также может быть преобразована относительно легко, хотя и не так тривиально, как с основаниями 2 и 4. Каждая восьмеричная цифра соответствует трем двоичным цифрам, а не четырем. Таким образом, мы можем преобразовывать восьмеричную и шестнадцатеричную системы с помощью промежуточного преобразования в двоичную, а затем перегруппировывать двоичные цифры в группы по три или четыре.
Деление-остаток в исходной базе
Как и для всех оснований, существует простой алгоритм для преобразования представления числа в шестнадцатеричное посредством выполнения операций целочисленного деления и остатка в исходном основании. Теоретически это возможно для любого основания, но для большинства людей только десятичное, а для большинства компьютеров только двоичное (которое можно преобразовать гораздо более эффективными методами) может быть легко обработано этим методом.
Пусть d — число, которое нужно представить в шестнадцатеричной системе счисления, а ряд h i h i−1 ...h 2 h 1 — шестнадцатеричные цифры, представляющие это число.
- я ← 1
- ч я ← д мод 16
- д ← (д − х i ) / 16
- Если d = 0 (возврат ряда h i ), в противном случае увеличиваем i и переходим к шагу 2
«16» можно заменить любой другой базой по желанию.
Ниже представлена реализация JavaScript указанного выше алгоритма для преобразования любого числа в шестнадцатеричное в строковом представлении. Ее цель — проиллюстрировать указанный выше алгоритм. Однако для серьезной работы с данными гораздо целесообразнее работать с побитовыми операторами .
функция toHex ( d ) { var r знак равно d % 16 ; if ( d - r == 0 ) { return toChar ( r ); } return toHex (( d - r ) / 16 ) + toChar ( r ); } function toChar ( n ) { const Alpha = "0123456789ABCDEF" ; вернуть альфу . charAt ( n ); } Преобразование посредством сложения и умножения

Также возможно выполнить преобразование, присвоив каждому месту в исходной базе шестнадцатеричное представление его значения места — перед выполнением умножения и сложения для получения окончательного представления. Например, чтобы преобразовать число B3AD в десятичное, можно разбить шестнадцатеричное число на его цифры: B (11 10 ), 3 (3 10 ), A (10 10 ) и D (13 10 ), а затем получить окончательный результат, умножив каждое десятичное представление на 16 p ( p — соответствующая шестнадцатеричная цифра, считая справа налево, начиная с 0). В этом случае мы имеем следующее:
B3AD = (11 × 16 3 ) + (3 × 16 2 ) + (10 × 16 1 ) + (13 × 16 0 )
что составляет 45997 в десятичной системе счисления.
Инструменты для преобразования
Многие компьютерные системы предоставляют утилиту-калькулятор, способную выполнять преобразования между различными основаниями, часто включая шестнадцатеричные.
В Microsoft Windows утилиту Калькулятор можно установить в режим Программиста, который позволяет выполнять преобразования между основаниями 16 (шестнадцатеричными), 10 (десятичными), 8 ( восьмеричными ) и 2 ( двоичными ), основаниями, наиболее часто используемыми программистами. В режиме Программиста экранная цифровая клавиатура включает шестнадцатеричные цифры от A до F, которые активны при выборе «Hex». Однако в шестнадцатеричном режиме Калькулятор Windows поддерживает только целые числа.
Элементарная арифметика
Элементарные операции, такие как деление, могут быть выполнены косвенно путем преобразования в альтернативную систему счисления , например, в широко используемую десятичную систему или двоичную систему, где каждая шестнадцатеричная цифра соответствует четырем двоичным цифрам.
В качестве альтернативы можно также выполнять элементарные операции непосредственно в самой шестнадцатеричной системе — полагаясь на ее таблицы сложения/умножения и соответствующие стандартные алгоритмы, такие как деление в столбик и традиционный алгоритм вычитания.
Реальные цифры
Рациональные числа
Как и другие системы счисления, шестнадцатеричная система может использоваться для представления рациональных чисел , хотя повторяющиеся разложения являются обычным явлением, поскольку шестнадцать (10 16 ) имеет только один простой делитель: два.
Для любого основания 0,1 (или «1/10») всегда эквивалентно единице, деленной на представление этого базового значения в его собственной системе счисления. Таким образом, будь то деление одного на два для двоичной системы счисления или деление одного на шестнадцать для шестнадцатеричной системы счисления, обе эти дроби записываются как 0.1. Поскольку основание 16 является полным квадратом (4 2 ), дроби, выраженные в шестнадцатеричной системе счисления, имеют нечетный период гораздо чаще, чем десятичные, и нет циклических чисел (кроме тривиальных однозначных цифр). Повторяющиеся цифры отображаются, когда знаменатель в наименьших членах имеет простой множитель, не найденный в основании; таким образом, при использовании шестнадцатеричной записи все дроби со знаменателями, которые не являются степенью двойки, приводят к бесконечной строке повторяющихся цифр (например, терций и квинтов). Это делает шестнадцатеричную (и двоичную) систему счисления менее удобной, чем десятичная, для представления рациональных чисел, поскольку большая часть лежит за пределами ее диапазона конечного представления.
Все рациональные числа, конечно представимые в шестнадцатеричной системе, также конечно представимы в десятичной, двенадцатеричной и шестидесятеричной : то есть любое шестнадцатеричное число с конечным числом цифр также имеет конечное число цифр, когда выражено в этих других основаниях. И наоборот, только часть тех, которые конечно представимы в последних основаниях, конечно представимы в шестнадцатеричной системе. Например, десятичное 0,1 соответствует бесконечно повторяющемуся представлению 0,1 9 в шестнадцатеричной системе. Однако шестнадцатеричная система более эффективна, чем двенадцатеричная и шестидесятеричная, для представления дробей со степенями двойки в знаменателе. Например, 0,0625 10 (одна шестнадцатая) эквивалентно 0,1 16 , 0,09 12 и 0;3,45 60 .
| н | Простые десятичные множители: основания, b = 10: 2 , 5 ; b − 1 = 9: 3 ; b + 1 = 11: 11 | Шестнадцатеричные простые множители: основания, b = 16 10 = 10: 2 ; b − 1 = 15 10 = F: 3, 5 ; b + 1 = 17 10 = 11: 11 | ||||
|---|---|---|---|---|---|---|
| Взаимный | Простые множители | Позиционное представление (десятичное) | Позиционное представление (шестнадцатеричное) | Простые множители | Взаимный | |
| 2 | 1/2 | 2 | 0,5 | 0,8 | 2 | 1/2 |
| 3 | 1/3 | 3 | 0. 3333... = 0. 3 | 0. 5555... = 0. 5 | 3 | 1/3 |
| 4 | 1/4 | 2 | 0,25 | 0,4 | 2 | 1/4 |
| 5 | 1/5 | 5 | 0.2 | 0. 3 | 5 | 1/5 |
| 6 | 1/6 | 2 , 3 | 0,1 6 | 0,2 А | 2 , 3 | 1/6 |
| 7 | 1/7 | 7 | 0. 142857 | 0.249 | 7 | 1/7 |
| 8 | 1/8 | 2 | 0,125 | 0.2 | 2 | 1/8 |
| 9 | 1/9 | 3 | 0. 1 | 0. 1С7 | 3 | 1/9 |
| 10 | 1/10 | 2 , 5 | 0.1 | 0.1 9 | 2 , 5 | 1/А |
| 11 | 1/11 | 11 | 0. 09 | 0. 1745D | Б | 1/Б |
| 12 | 1/12 | 2 , 3 | 0,08 3 | 0.1 5 | 2 , 3 | 1/С |
| 13 | 1/13 | 13 | 0.076923 | 0. 13Б | Д | 1/Д |
| 14 | 1/14 | 2 , 7 | 0.0 714285 | 0,1 249 | 2 , 7 | 1/Э |
| 15 | 1/15 | 3 , 5 | 0.0 6 | 0. 1 | 3 , 5 | 1/Эт |
| 16 | 1/16 | 2 | 0,0625 | 0.1 | 2 | 1/10 |
| 17 | 1/17 | 17 | 0. 0588235294117647 | 0. 0Ф | 11 | 1/11 |
| 18 | 1/18 | 2 , 3 | 0.0 5 | 0.0 Е38 | 2 , 3 | 1/12 |
| 19 | 1/19 | 19 | 0. 052631578947368421 | 0. 0D79435E5 | 13 | 1/13 |
| 20 | 1/20 | 2 , 5 | 0,05 | 0,0 С | 2 , 5 | 1/14 |
| 21 | 1/21 | 3 , 7 | 0.047619 | 0. 0C3 | 3 , 7 | 1/15 |
| 22 | 1/22 | 2 , 11 | 0.0 45 | 0.0 BA2E8 | 2 , Б | 1/16 |
| 23 | 1/23 | 23 | 0. 0434782608695652173913 | 0. 0B21642C859 | 17 | 1/17 |
| 24 | 1/24 | 2 , 3 | 0,041 6 | 0,0 А | 2 , 3 | 1/18 |
| 25 | 1/25 | 5 | 0,04 | 0. 0A3D7 | 5 | 1/19 |
| 26 | 1/26 | 2 , 13 | 0.0 384615 | 0.0 9D8 | 2 , Д | 1/1А |
| 27 | 1/27 | 3 | 0.037 | 0. 097B425ED | 3 | 1/1Б |
| 28 | 1/28 | 2 , 7 | 0.03 571428 | 0.0 924 | 2 , 7 | 1/1С |
| 29 | 1/29 | 29 | 0. 0344827586206896551724137931 | 0. 08D3DCB | 1D | 1/1D |
| 30 | 1/30 | 2 , 3 , 5 | 0.0 3 | 0.0 8 | 2 , 3 , 5 | 1/1E |
| 31 | 1/31 | 31 | 0. 032258064516129 | 0.08421 | 1 этаж | 1/1F |
| 32 | 1/32 | 2 | 0,03125 | 0,08 | 2 | 1/20 |
| 33 | 1/33 | 3 , 11 | 0. 03 | 0. 07C1F | 3 , Б | 1/21 |
| 34 | 1/34 | 2 , 17 | 0.0 2941176470588235 | 0.0 78 | 2 , 11 | 1/22 |
| 35 | 1/35 | 5 , 7 | 0.0 285714 | 0.075 | 5 , 7 | 1/23 |
| 36 | 1/36 | 2 , 3 | 0,02 7 | 0,0 71С | 2 , 3 | 1/24 |
| 37 | 1/37 | 37 | 0.027 | 0.06EB3E453 | 25 | 1/25 |
Иррациональные числа
В таблице ниже приведены разложения некоторых распространенных иррациональных чисел в десятичной и шестнадцатеричной системе счисления.
| Число | Позиционное представительство | |
|---|---|---|
| Десятичная дробь | Шестнадцатеричный | |
| √ 2 (длина диагонали единичного квадрата ) | 1.414 213 562 373 095 048 ... | 1.6A09E667F3BCD... |
| √ 3 (длина диагонали единичного куба ) | 1.732 050 807 568 877 293 ... | 1.BB67AE8584CAA... |
| √ 5 (длина диагонали прямоугольника 1 ×2) | 2.236 067 977 499 789 696 ... | 2.3C6EF372FE95... |
| φ (фи, золотое сечение = (1+ √ 5 )/2 ) | 1.618 033 988 749 894 848 ... | 1.9E3779B97F4A... |
| π (пи, отношение длины окружности к диаметру ) | 3.141 592 653 589 793 238 462 643 383 279 502 884 197 169 399 375 105 ... | 3.243F6A8885A308D313198A2E0 3707344A4093822299F31D008... |
| е (основание натурального логарифма ) | 2.718 281 828 459 045 235 ... | 2.B7E151628AED2A6B... |
| τ ( константа Туэ–Морса ) | 0,412 454 033 640 107 597 ... | 0,6996 9669 9669 6996... |
| γ (предельная разность между гармоническим рядом и натуральным логарифмом) | 0,577 215 664 901 532 860 ... | 0.93C467E37DB0C7A4D1B... |
Полномочия
Степени двойки имеют очень простые расширения в шестнадцатеричной системе. Первые шестнадцать степеней двойки показаны ниже.
| 2 х | Ценить | Значение (десятичное) |
|---|---|---|
| 2 0 | 1 | 1 |
| 2 1 | 2 | 2 |
| 2 2 | 4 | 4 |
| 2 3 | 8 | 8 |
| 2 4 | 10 гекс | 16 дек. |
| 2 5 | 20 гекс | 32 дек. |
| 2 6 | 40 гекс | 64 дек. |
| 2 7 | 80 гекс | 128 дек. |
| 2 8 | 100 гекс | 256 дек. |
| 2 9 | 200 гекс | 512 дек. |
| 2 А (2 10 дек ) | 400 гекс | 1024 дек. |
| 2 Б (2 11 дек .) | 800 гекс | 2048 дек. |
| 2 С (2 12 дек ) | 1000 гекс | 4096 дек. |
| 2 Д (2 13 дек ) | 2000 шестнадцатеричный | 8192 дек. |
| 2 В (2 14 дек .) | 4000 гекс | 16,384 дек. |
| 2 Ф (2 15 дек .) | 8000 шестнадцатеричный | 32,768 дек. |
| 2 10 (2 16 дек ) | 10000 гекс | 65,536 дек. |
Культурная история
Традиционные китайские единицы измерения были шестнадцатеричными. Например, один цзинь (斤) в старой системе равен шестнадцати таэлям . Суаньпань (китайские счеты ) можно использовать для выполнения шестнадцатеричных вычислений, таких как сложение и вычитание. [31]
Как и в случае с двенадцатеричной системой, время от времени предпринимались попытки продвигать шестнадцатеричную систему как предпочтительную систему счисления. Эти попытки часто предлагают определенное произношение и символы для отдельных цифр. [32] Некоторые предложения унифицируют стандартные меры так, чтобы они были кратны 16. [33] [34] Одно из первых таких предложений было выдвинуто Джоном В. Нистромом в «Проекте новой системы арифметики, веса, меры и монет: предложено назвать тональной системой с шестнадцатью в основании» , опубликованном в 1862 году. [35] Нистром среди прочего предложил шестнадцатеричное время , которое подразделяет день на 16, так что в дне 16 «часов» (или «10 тимов », произносится как тонтим ). [36]
Слово hexadecimal впервые зафиксировано в 1952 году. [37] Оно макароническое в том смысле, что сочетает в себе греческое ἕξ (hex) «шесть» с латинским -decimal . Полностью латинская альтернатива sexadecimal (сравните слово sexagesimal для основания 60) старше и, по крайней мере, изредка используется с конца 19 века. [38] Оно все еще используется в 1950-х годах в документации Bendix . Шварцман (1994) утверждает, что использование sexadecimal , возможно, было исключено из-за его предполагаемого сокращения до sex . [39] Многие западные языки с 1960-х годов приняли термины, эквивалентные по построению шестнадцатеричной системе (например, французский hexadécimal , итальянский esadecimale , румынский hexazecimal , сербский хексадецимални и т. д.), но другие ввели термины, которые заменяют родные слова для «шестнадцать» (например, греческий δεκαεξαδικός, исландский sextándakerfi , русский шестнадцатеричной и т. д.)
Терминология и обозначения не были устоявшимися до конца 1960-х годов. В 1969 году Дональд Кнут утверждал, что этимологически правильным термином будет sevenary или, возможно , sedenary , латинский термин, предназначенный для обозначения «сгруппированный по 16» по образцу двоичной , троичной , четверичной и т. д. Согласно аргументу Кнута, правильными терминами для десятичной и восьмеричной арифметики будут денарный и октонарный соответственно. [40] Альфред Б. Тейлор использовал sevenary в своей работе середины 1800-х годов об альтернативных основаниях счисления, хотя он отверг основание 16 из-за его «неудобного количества цифр». [41] [42]
Текущая нотация, использующая буквы от A до F, становится фактическим стандартом с 1966 года, после публикации руководства Fortran IV для IBM System/360 , которое (в отличие от более ранних вариантов Fortran) признает стандарт для ввода шестнадцатеричных констант. [43] Как отмечено выше, альтернативные нотации использовались NEC (1960) и The Pacific Data Systems 1020 (1964). Стандарт, принятый IBM, по-видимому, стал широко распространенным к 1968 году, когда Брюс Алан Мартин в своем письме редактору CACM жалуется , что
С нелепым выбором букв A, B, C, D, E, F в качестве шестнадцатеричных числовых символов, добавляющим и без того неприятные проблемы различения восьмеричных (или шестнадцатеричных) чисел от десятичных чисел (или имен переменных), настало время пересмотреть наши числовые символы. Это следовало сделать до того, как неудачный выбор превратился в фактический стандарт!
Аргумент Мартина состоял в том, что использование цифр от 0 до 9 в недесятеричных числах «подразумевает для нас схему счисления с основанием в десять»: «Почему бы не использовать совершенно новые символы (и названия) для семи или пятнадцати ненулевых цифр, необходимых в восьмеричной или шестнадцатеричной системе. Даже использование букв от A до P было бы улучшением, но совершенно новые символы могли бы отражать двоичную природу системы». [19] Он также утверждал, что «повторное использование букв алфавита для числовых цифр представляет собой гигантский шаг назад по сравнению с изобретением отдельных, неалфавитных глифов для цифр шестнадцать столетий назад» (как цифры брахми , а позднее в индо-арабской системе счисления ), и что последние стандарты ASCII (ASA X3.4-1963 и USAS X3.4-1968) «должны были сохранить шесть позиций кодовой таблицы после десяти десятичных цифр — вместо того, чтобы без необходимости заполнять их знаками пунктуации» (":;<=>?"), которые могли бы быть размещены в другом месте среди 128 доступных позиций.
Base16 (кодирование передачи)
Base16 (как имя собственное без пробела) может также относиться к двоично-текстовой кодировке, принадлежащей к тому же семейству, что и Base32 , Base58 и Base64 .
В этом случае данные разбиваются на 4-битные последовательности, и каждое значение (от 0 до 15 включительно) кодируется с использованием одного из 16 символов из набора символов ASCII . Хотя могут использоваться любые 16 символов из набора символов ASCII, на практике всегда выбираются цифры ASCII "0"–"9" и буквы "A"–"F" (или строчные "a"–"f"), чтобы соответствовать стандартной письменной нотации для шестнадцатеричных чисел.
Кодирование Base16 имеет ряд преимуществ:
- Большинство языков программирования уже имеют средства для анализа шестнадцатеричных чисел в кодировке ASCII.
- Поскольку 4 бита равны ровно половине байта, их легче обрабатывать, чем 5 или 6 бит Base32 и Base64 соответственно.
- Символы 0–9 и A–F являются универсальными в шестнадцатеричной системе счисления, поэтому их легко понять с первого взгляда, не прибегая к помощи таблицы соответствия символов.
- Многие архитектуры ЦП имеют специальные инструкции, которые позволяют получить доступ к полубайту (иначе называемому « полубайтом »), что делает его более эффективным на аппаратном уровне, чем Base32 и Base64.
Основными недостатками кодирования Base16 являются:
- Эффективность использования пространства составляет всего 50%, поскольку каждое 4-битное значение исходных данных будет закодировано как 8-битный байт. Напротив, кодировки Base32 и Base64 имеют эффективность использования пространства 63% и 75% соответственно.
- Возможная дополнительная сложность из-за необходимости принимать как заглавные, так и строчные буквы
Поддержка кодировки Base16 повсеместно распространена в современных вычислениях. Она является основой для стандарта W3C для процентного кодирования URL , где символ заменяется знаком процента "%" и его формой в кодировке Base16. Большинство современных языков программирования напрямую включают поддержку форматирования и анализа чисел в кодировке Base16.
Смотрите также
- Base32 , Base64 (схемы кодирования контента)
- Шестнадцатеричное время
- Шестнадцатеричный формат с плавающей точкой IBM
- Hex-редактор
- Шестнадцатеричный дамп
- Формула Бейли-Борвейна-Плуффа (ББП)
- Hexspeak
- P-обозначение
Ссылки
- ^ "Шестнадцатеричная система". Ionos Digital Guide . Архивировано из оригинала 2022-08-26 . Получено 2022-08-26 .
- ^ Кнут, Дональд Эрвин (1986). TeXbook. Дуэйн Бибби. Рединг, Массачусетс. ISBN 0-201-13447-0. OCLC 12973034. Архивировано из оригинала 2022-01-16 . Получено 2022-03-15 .
{{cite book}}: CS1 maint: location missing publisher (link) - ^ Строка
"\x1B[0m\x1B[25;1H"определяет последовательность символов Esc [ 0 m Esc [ 2 5; 1 H . Это управляющие последовательности, используемые на терминале ANSI , которые сбрасывают набор символов и цвет, а затем перемещают курсор на строку 25. - ^ "Стандарт Unicode, версия 7" (PDF) . Unicode . Архивировано (PDF) из оригинала 2016-03-03 . Получено 2018-10-28 .
- ^ "Modula-2 – Vocabulary and representation". Modula −2 . Архивировано из оригинала 2015-12-13 . Получено 2015-11-01 .
- ^ "Введение в типы данных VHDL". Учебное пособие по FPGA . 2020-05-10. Архивировано из оригинала 2020-08-23 . Получено 2020-08-21 .
- ^ "*read-base* variable in Common Lisp". CLHS . Архивировано из оригинала 2016-02-03 . Получено 2015-01-10 .
- ^ "*print-base* variable in Common Lisp". CLHS . Архивировано из оригинала 2014-12-26 . Получено 2015-01-10 .
- ↑ MSX на подходе — Часть 2: Внутри MSX. Архивировано 24 ноября 2010 г. в Wayback Machine Compute!, выпуск 56, январь 1985 г., стр. 52.
- ^ Программы BBC BASIC не полностью переносимы на Microsoft BASIC (без изменений), поскольку последний требует
&префикса восьмеричных значений. (Microsoft BASIC в основном использует&Oпрефикс восьмеричных чисел и&Hпрефикс шестнадцатеричных чисел, но амперсанд сам по себе даёт интерпретацию по умолчанию как восьмеричного префикса.) - ^ "Объяснение шестнадцатеричных веб-цветов". Архивировано из оригинала 2006-04-22 . Получено 2006-01-11 .
- ^ "ISO-8859-1 (ISO Latin 1) Character Encoding". www.ic.unicamp.br . Архивировано из оригинала 2019-06-29 . Получено 2019-06-26 .
- ^ abcdefg Savard, John JG (2018) [2005]. "Компьютерная арифметика". quadibloc . Ранние дни шестнадцатеричной системы счисления. Архивировано из оригинала 2018-07-16 . Получено 2018-07-16 .
- ^ "2.1.3 Шестнадцатеричная система счисления". Справочное руководство программиста G15D (PDF) . Лос-Анджелес, Калифорния, США: Bendix Computer , Division of Bendix Aviation Corporation . стр. 4. Архивировано (PDF) из оригинала 01.06.2017 . Получено 01.06.2017 .
Эта база используется, поскольку группа из четырех бит может представлять любое из шестнадцати различных чисел (от нуля до пятнадцати). Назначая символ каждой из этих комбинаций, мы приходим к нотации, называемой шестнадцатеричной (обычно "шестнадцатеричной" в разговоре, потому что никто не хочет сокращать "секс"). Символами в шестнадцатеричном языке являются десять десятичных цифр, а на пишущей машинке G-15 — буквы "u", "v", "w", "x", "y" и "z". Это произвольные обозначения; другие компьютеры могут использовать другие символы алфавита для этих последних шести цифр.
- ^ Gill, S.; Neagher, RE; Muller, DE; Nash, JP; Robertson, JE; Shapin, T.; Whesler, DJ (1956-09-01). Nash, JP (ред.). "ILLIAC Programming – A Guide to the Preparation of Problems For Solution by the University of Illinois Digital Computer" (PDF) . bitsavers.org (Четвертое издание. Исправленное и исправленное издание). Urbana, Illinois, US: Digital Computer Laboratory, Graduate College, University of Illinois . стр. 3–2. Архивировано (PDF) из оригинала 2017-05-31 . Получено 2014-12-18 .
- ↑ Royal Precision Electronic Computer LGP – 30 Programming Manual. Порт-Честер, Нью-Йорк: Royal McBee Corporation . Апрель 1957. Архивировано из оригинала 2017-05-31 . Получено 2017-05-31 .(Примечание. Эта несколько странная последовательность была из следующих шести последовательных цифровых кодов клавиатуры в 6-битном коде символов LGP-30 .)
- ^ Манти, Штеффен; Лейбрандт, Клаус (2 июля 2002 г.). «Die PERM und ALGOL» (PDF) (на немецком языке). Архивировано (PDF) из оригинала 3 октября 2018 г. Проверено 19 мая 2018 г.
- ^ NEC Parametron Digital Computer Type NEAC-1103 (PDF) . Токио, Япония: Nippon Electric Company Ltd. 1960. Кат. № 3405-C. Архивировано (PDF) из оригинала 2017-05-31 . Получено 2017-05-31 .
- ^ abc Martin, Bruce Alan (октябрь 1968 г.). «Письма редактору: О двоичной нотации». Сообщения ACM . 11 (10). Associated Universities Inc. : 658. doi : 10.1145/364096.364107 . S2CID 28248410.
- ^ ab Whitaker, Ronald O. (январь 1972 г.). Написано в Индианаполисе, штат Индиана, США. "More on man/machine" (PDF) . Letters. Datamation . Vol. 18, no. 1. Barrington, Illinois, US: Technical Publishing Company . p. 103. Архивировано (PDF) из оригинала 2022-12-05 . Получено 2022-12-24 .(1 страница)
- ^ ab Whitaker, Ronald O. (1976-08-10) [1975-02-24]. "Комбинированный дисплей и селектор диапазона для использования с цифровыми приборами, использующими двоичную систему исчисления" (PDF) . Индианаполис, Индиана, США. Патент США 3974444A. Архивировано (PDF) из оригинала 2022-12-24 . Получено 2022-12-24 .(7 страниц)
- ^ "SN5446A, '47A, '48, SN54LS47, 'LS48, 'LS49, SN7446A, '47A, '48, SN74LS47, 'LS48, 'LS49 Декодеры/драйверы BCD-в-семисегментный". Даллас, Техас, США: Texas Instruments Incorporated . Март 1988 [1974]. SDLS111. Архивировано (PDF) из оригинала 20-10-2021 . Получено 15-09-2021 .(29 страниц)
- ^ abc Magnuson, Robert A. (январь 1968). "Руководство по шестнадцатеричному произношению". Datamation . Т. 14, № 1. С. 45.
- ^ ab Rogers, SR (2007). "Шестнадцатеричные числовые слова". Intuitor . Архивировано из оригинала 2019-09-17 . Получено 2019-08-26 .
- ^ Бабб, Тим (2015). «Как произносить шестнадцатеричное». Bzarg . Архивировано из оригинала 2020-11-11 . Получено 2021-01-01 .
- ^ Кларк, Артур; Поль, Фредерик (2008). Последняя теорема . Баллантайн. стр. 91. ISBN 978-0007289981.
- ^ "ISO/IEC 9899:1999 – Языки программирования – C". ISO . Iso.org. 2011-12-08. Архивировано из оригинала 2016-10-10 . Получено 2014-04-08 .
- ^ "Rationale for International Standard – Programming Languages – C" (PDF) . Open Standards . 5.10. Апрель 2003 г. стр. 52, 153–154, 159. Архивировано (PDF) из оригинала 2016-06-06 . Получено 2010-10-17 .
- ^ IEEE и The Open Group (2013) [2001]. "dprintf, fprintf, printf, snprintf, sprintf – print formatted output". The Open Group Base Specifications (Выпуск 7, IEEE Std 1003.1, 2013 ed.). Архивировано из оригинала 21.06.2016 . Получено 21.06.2016 .
- ^ ab Mano, M. Morris; Ciletti, Michael D. (2013). Digital Design – With an Introduction to the Verilog HDL (Пятое изд.). Pearson Education . С. 6, 8–10. ISBN 978-0-13-277420-8.
- ^ "算盤 Шестнадцатеричное сложение и вычитание на китайских счетах". totton.idirect.com . Архивировано из оригинала 2019-07-06 . Получено 2019-06-26 .
- ^ "Предложение шестнадцатеричного символа с основанием 4^2". Hauptmech . Архивировано из оригинала 2021-10-20 . Получено 04.09.2008 .
- ^ "Intuitor Hex Headquarters". Intuitor . Архивировано из оригинала 2010-09-04 . Получено 2018-10-28 .
- ^ Нимиетц, Рикардо Канчо (21.10.2003). "Предложение о добавлении шести шестнадцатеричных цифр (AF) в Unicode" (PDF) . ISO/IEC JTC1/SC2/WG2 . Получено 25.06.2024 .
- ↑ Нистром, Джон Уильям (1862). Проект новой системы арифметики, веса, меры и монет: предложено назвать ее тональной системой с шестнадцатью основаниями. Филадельфия: Липпинкотт.
- ^ Нистром (1862), стр. 33: «При выражении времени, угла окружности или точек на компасе единицу тим следует обозначать как целое число, а ее части — как тональные дроби , например, 5·86 тим — это пять раз и метонби [*"sutim and metonby" Джон Нистром случайно приводит часть числа в десятичных именах; в схеме произношения Нистрома 5=su, 8=me, 6=by, см. unifoundry.com Архивировано 19 мая 2021 г. на Wayback Machine ].»
- ^ CE Fröberg, Таблицы шестнадцатеричного преобразования , Лунд (1952).
- ^ В словаре Century Dictionary 1895 года термин «шестнадцатеричный» употребляется в более общем смысле «относящийся к шестнадцати». Раннее явное использование термина «шестнадцатеричный» в смысле «использующий основание 16» также встречается в 1895 году в Journal of the American Geographical Society of New York , vols. 27–28, p. 197.
- ^ Шварцман, Стивен (1994). Слова математики: Этимологический словарь математических терминов, используемых в английском языке . Математическая ассоциация Америки. стр. 105. ISBN 0-88385-511-9.sv шестнадцатеричный
- ^ Кнут, Дональд. (1969). Искусство программирования , том 2. ISBN 0-201-03802-1 . (Глава 17.)
- ↑ Альфред Б. Тейлор, Отчет о мерах и весах, Фармацевтическая ассоциация, 8-я ежегодная сессия, Бостон, 15 сентября 1859 г. См. страницы 33 и 41.
- ↑ Альфред Б. Тейлор, «Восьмеричная нумерация и ее применение к системе мер и весов», Proc Amer. Phil. Soc. Vol XXIV Архивировано 24 июня 2016 г. в Wayback Machine , Филадельфия, 1887 г.; страницы 296–366. См. страницы 317 и 322.
- ^ Язык IBM System/360 FORTRAN IV. Архивировано 19 мая 2021 г. в Wayback Machine (1966), стр. 13.
