Функция Эйлера

В теории чисел функция Эйлера тотиент подсчитывает положительные целые числа вплоть до заданного целого числа n, которые взаимно просты с n . Она записывается с использованием греческой буквы фи как или , и может также называться функцией Эйлера фи . Другими словами, это количество целых чисел k в диапазоне 1 ≤ k ≤ n, для которых наибольший общий делитель gcd( n , k ) равен 1. [2] [3] Целые числа k этой формы иногда называют тотативами n .
Например, тотативы числа n = 9 — это шесть чисел 1, 2, 4, 5, 7 и 8. Все они взаимно просты с 9, но три других числа в этом диапазоне, 3, 6 и 9, таковыми не являются, поскольку gcd(9, 3) = gcd(9, 6) = 3 и gcd(9, 9) = 9. Следовательно, φ (9) = 6. В качестве другого примера, φ (1) = 1 , поскольку для n = 1 единственное целое число в диапазоне от 1 до n — это само 1, а gcd(1, 1) = 1 .
Функция Эйлера является мультипликативной функцией , то есть если два числа m и n являются взаимно простыми, то φ ( mn ) = φ ( m ) φ ( n ) . [4] [5] Эта функция определяет порядок мультипликативной группы целых чисел по модулю n ( группы единиц кольца ) . [6] Она также используется для определения системы шифрования RSA .
История, терминология и обозначения
Леонард Эйлер ввел функцию в 1763 году. [7] [8] [9] Однако в то время он не выбрал какой-либо конкретный символ для ее обозначения. В публикации 1784 года Эйлер изучил функцию далее, выбрав греческую букву π для ее обозначения: он написал πD для «множества чисел, меньших D , и которые не имеют с ним общего делителя». [10] Это определение отличается от текущего определения для функции тотиента при D = 1, но в остальном то же самое. Ныне стандартное обозначение [8] [11] φ ( A ) происходит из трактата Гаусса 1801 года Disquisitiones Arithmeticae , [12] [13] хотя Гаусс не использовал скобки вокруг аргумента и писал φA . Таким образом, ее часто называют фи-функцией Эйлера или просто фи-функцией .
В 1879 году Дж. Дж. Сильвестр ввел термин тотиент для этой функции, [14] [15] поэтому ее также называют функцией тотиента Эйлера , тотиентом Эйлера или тотиентом Эйлера . Тотиент Жордана является обобщением тотиента Эйлера.
Коэффициент числа n определяется как n − φ ( n ) . Он подсчитывает количество положительных целых чисел, меньших или равных n , которые имеют хотя бы один общий простой множитель с n .
Вычисление функции Эйлера
Существует несколько формул для вычисления φ ( n ) .
Формула произведения Эйлера
В нем говорится:
где произведение берется по различным простым числам, делящим n . (Обозначения см. в разделе Арифметическая функция .)
Эквивалентная формулировка имеет вид: где — разложение на простые множители (то есть — различные простые числа).
Доказательство этих формул зависит от двух важных фактов.
Фи — мультипликативная функция
Это означает, что если gcd( m , n ) = 1 , то φ ( m ) φ ( n ) = φ ( mn ) . Схема доказательства: Пусть A , B , C — множества положительных целых чисел, которые взаимно просты с m , n , mn и меньше их соответственно, так что | A | = φ ( m ) и т. д. Тогда между A × B и C существует биекция по китайской теореме об остатках .
Значение phi для аргумента простой мощности
Если p — простое число и k ≥ 1 , то
Доказательство : Поскольку p — простое число, единственными возможными значениями gcd( p k , m ) являются 1, p , p 2 , ..., p k , и единственный способ получить gcd( p k , m ) > 1 — это если m кратно p , то есть m ∈ { p , 2 p , 3 p , ..., p k − 1 p = p k } , и существует p k − 1 таких кратных, не больших p k . Следовательно, все остальные числа p k − p k − 1 взаимно просты с p k .
Доказательство формулы произведения Эйлера
Основная теорема арифметики гласит, что если n > 1, то существует единственное выражение , где p 1 < p 2 < ... < p r — простые числа , а каждое k i ≥ 1. (Случай n = 1 соответствует пустому произведению.) Многократное использование мультипликативного свойства φ и формулы для φ ( p k ) дает
Это дает обе версии формулы произведения Эйлера.
Альтернативное доказательство, не требующее мультипликативного свойства, вместо этого использует принцип включения-исключения, примененный к множеству , исключая множества целых чисел, делящихся на простые делители.
Пример
Проще говоря: различными простыми множителями числа 20 являются 2 и 5; половина из двадцати целых чисел от 1 до 20 делятся на 2, что оставляет десять; пятая часть из них делится на 5, что оставляет восемь чисел, взаимно простых с 20; это: 1, 3, 7, 9, 11, 13, 17, 19.
Альтернативная формула использует только целые числа:
преобразование Фурье
Тотиент — это дискретное преобразование Фурье от НОД , оцененное как 1. [16] Пусть
где x k = gcd( k , n ) для k ∈ {1, ..., n } . Тогда
Действительная часть этой формулы равна
Например, используя и : В отличие от произведения Эйлера и формулы суммы делителей, эта не требует знания множителей n . Однако она включает вычисление наибольшего общего делителя n и каждого положительного целого числа, меньшего n , чего в любом случае достаточно для факторизации.
Сумма делителей
Установленное Гауссом свойство [17] заключается в том, что
где сумма берется по всем положительным делителям d числа n , можно доказать несколькими способами. (См. Арифметические функции для ознакомления с соглашениями об обозначениях.)
Одно доказательство состоит в том, чтобы заметить, что φ ( d ) также равно числу возможных генераторов циклической группы C d ; в частности, если C d = ⟨ g ⟩ с g d = 1 , то g k является генератором для каждого k , взаимно простого с d . Поскольку каждый элемент C n порождает циклическую подгруппу , а каждая подгруппа C d ⊆ C n порождается ровно φ ( d ) элементами C n , формула следует. [18] Эквивалентно, формула может быть выведена тем же аргументом, примененным к мультипликативной группе корней n -й степени из единицы и примитивных корней d -й степени из единицы .
Формулу можно также вывести из элементарной арифметики. [19] Например, пусть n = 20 и рассмотрим положительные дроби до 1 со знаменателем 20:
Изложите их в самых простых выражениях:
Все эти двадцать дробей положительные .к/г ≤ 1, знаменатели которых являются делителями d = 1, 2, 4, 5, 10, 20. Дроби со знаменателем 20 — это те, числители которых взаимно просты с 20, а именно 1/20 , 3/20 , 7/20 , 9/20 , 11/20 , 13/20 , 17/20 , 19/20 ; по определению это дроби φ (20) . Аналогично, существуют дроби φ (10) со знаменателем 10 и дроби φ (5) со знаменателем 5 и т. д. Таким образом, набор из двадцати дробей разбивается на подмножества размера φ ( d ) для каждого d, делящего 20. Аналогичный аргумент применим для любого n.
Инверсия Мёбиуса , примененная к формуле суммы делителей, дает
где μ — функция Мёбиуса , мультипликативная функция , определяемая и для каждого простого числа p и k ≥ 2. Эту формулу можно также вывести из формулы произведения, умножив ее, чтобы получить
Пример:
Некоторые ценности
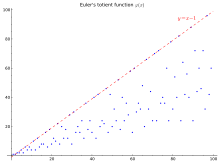
Первые 100 значений (последовательность A000010 в OEIS ) показаны в таблице и графике ниже:
φ ( n ) для 1 ≤ n ≤ 100 + 1 2 3 4 5 6 7 8 9 10 0 1 1 2 2 4 2 6 4 6 4 10 10 4 12 6 8 8 16 6 18 8 20 12 10 22 8 20 12 18 12 28 8 30 30 16 20 16 24 12 36 18 24 16 40 40 12 42 20 24 22 46 16 42 20 50 32 24 52 18 40 24 36 28 58 16 60 60 30 36 32 48 20 66 32 44 24 70 70 24 72 36 40 36 60 24 78 32 80 54 40 82 24 64 42 56 40 88 24 90 72 44 60 46 72 32 96 42 60 40
На графике справа верхняя линия y = n − 1 является верхней границей, действительной для всех n, кроме единицы, и достигается тогда и только тогда, когда n является простым числом. Простая нижняя граница — , которая довольно свободна: на самом деле, нижняя граница графика пропорциональна н/лог лог n . [20]
Теорема Эйлера
Это означает, что если a и n взаимно просты , то
Особый случай, когда n является простым числом, известен как малая теорема Ферма .
Это следует из теоремы Лагранжа и того факта, что φ ( n ) — порядок мультипликативной группы целых чисел по модулю n .
Криптосистема RSA основана на этой теореме: она подразумевает, что обратная функция a ↦ a e mod n , где e — (публичная) экспонента шифрования, есть функция b ↦ b d mod n , где d , (частная) экспонента дешифрования, есть мультипликативная обратная функция e по модулю φ ( n ) . Таким образом, сложность вычисления φ ( n ) без знания факторизации n — это сложность вычисления d : это известно как задача RSA , которая может быть решена путем факторизации n . Владелец закрытого ключа знает факторизацию, поскольку закрытый ключ RSA создается путем выбора n как произведения двух (случайно выбранных) больших простых чисел p и q . Только n публично раскрывается, и, учитывая сложность факторизации больших чисел, у нас есть гарантия, что никто другой не знает факторизацию.
Другие формулы
В частности:
Сравните это с формулой (см. наименьшее общее кратное ).
- φ ( n ) четно для n ≥ 3 .
Более того, если n имеет r различных нечетных простых множителей, 2 r | φ ( n )
- Для любых a > 1 и n > 6 , таких что 4 ∤ n, существует l ≥ 2 n, такое что l | φ ( a n − 1) .
где rad( n ) — радикал числа n (произведение всех различных простых чисел, делящих n ).
- [21]
- ( [22] цитируется в [23] )
- [Лю (2016)]
- [22]
- [24]
- [24]
(где γ — постоянная Эйлера–Маскерони ).
Личность Менона
В 1965 году П. Кесава Менон доказал
где d ( n ) = σ 0 ( n ) — количество делителей числа n .
Делимость на любое фиксированное положительное целое число
Следующее свойство, которое является частью « фольклора » (т.е., по-видимому, не опубликовано как конкретный результат: [25] см. введение к этой статье, в котором оно указано как «давно известное»), имеет важные последствия. Например, оно исключает равномерное распределение значений в арифметических прогрессиях по модулю для любого целого числа .
- Для каждого фиксированного положительного целого числа соотношение справедливо почти для всех , то есть для всех значений, кроме как .
Это является элементарным следствием того факта, что сумма обратных величин простых чисел, сравнимых по модулю 1, расходится, что само по себе является следствием доказательства теоремы Дирихле об арифметических прогрессиях .
Генерация функций
Ряд Дирихле для φ ( n ) можно записать в терминах дзета-функции Римана как: [26]
где левая часть сходится при .
Производящая функция ряда Ламберта [27]
который сходится при | q | < 1 .
Оба они доказываются с помощью элементарных преобразований рядов и формул для φ ( n ) .
Темпы роста
По словам Харди и Райта, порядок φ ( n ) «всегда „почти n “». [28]
Первый [29]
но когда n стремится к бесконечности, [30] для всех δ > 0
Эти две формулы можно доказать, используя немного больше, чем формулы для φ ( n ) и функции суммы делителей σ ( n ) .
На самом деле, при доказательстве второй формулы неравенство
верно для n > 1 , доказано.
У нас также есть [20]
Здесь γ — постоянная Эйлера , γ = 0,577215665... , поэтому e γ = 1,7810724... и e − γ = 0,56145948... .
Доказательство этого не совсем требует теоремы о простых числах . [31] [32] Поскольку log log n стремится к бесконечности, эта формула показывает, что
На самом деле, правда в большем. [33] [34] [35]
и
Второе неравенство было показано Жаном-Луи Николя . Рибенбойм говорит: «Метод доказательства интересен тем, что неравенство показано сначала при предположении, что гипотеза Римана верна, а затем при противоположном предположении». [35] : 173
Для среднего порядка имеем [22] [36]
благодаря Арнольду Вальфису , его доказательство, использующее оценки показательных сумм, принадлежит И. М. Виноградову и Н. М. Коробову . Комбинируя методы ван дер Корпута и Виноградова, Х.-К. Лю (On Euler's function. Proc. Roy. Soc. Edinburgh Sect. A 146 (2016), № 4, 769–775) улучшил ошибку до
(в настоящее время это самая известная оценка такого типа). «Большое О » обозначает величину, ограниченную константой, умноженной на функцию n внутри скобок (которая мала по сравнению с n 2 ).
Этот результат можно использовать для доказательства [37] , что вероятность того, что два случайно выбранных числа окажутся взаимно простыми, равна 6/π 2 .
Соотношение последовательных значений
В 1950 году Сомаяджулу доказал [38] [39]
В 1954 году Шинцель и Серпинский усилили это, доказав [38] [39] , что множество
плотно в положительных действительных числах. Они также доказали [38] , что множество
плотно в интервале (0,1).
Числа тотиентов
Тотиентное число — это значение функции тотиента Эйлера: то есть m , для которого существует по крайней мере одно n, для которого φ ( n ) = m . Валентность или кратность тотиента числа m — это количество решений этого уравнения. [40] Нетотиент — это натуральное число , которое не является тотиентным числом. Каждое нечетное целое число, превышающее 1, тривиально является нетотиентом. Существует также бесконечно много четных нетотиентов, [41] и, действительно, каждое положительное целое число имеет кратное, которое является четным нетотиентом. [42]
Число чисел до заданного предела x равно
для константы C = 0,8178146... . [43]
Если подсчитать по кратности, то число чисел-тотиентов до заданного предела x равно
где ошибка R имеет порядок не более х/(лог x ) k для любого положительного k . [44]
Известно, что кратность m превышает m δ бесконечно часто для любого δ < 0,55655 . [45] [46]
Теорема Форда
Форд (1999) доказал, что для каждого целого числа k ≥ 2 существует тотиентное число m кратности k : то есть, для которого уравнение φ ( n ) = m имеет ровно k решений; этот результат ранее был выдвинут Вацлавом Серпинским [47] и был получен как следствие гипотезы Шинцеля H. [ 43] Действительно, каждая встречающаяся кратность встречается бесконечно часто. [43] [46]
Однако не известно ни одного числа m с кратностью k = 1. Гипотеза Кармайкла о функции тотиента заключается в утверждении, что такого числа m не существует . [48]
Идеальные числа тотиента
Совершенное тотиентное число — это целое число, равное сумме своих итерированных тотиентов. То есть, мы применяем функцию тотиента к числу n , снова применяем ее к полученному тотиенту и так далее, пока не достигнем числа 1, и складываем полученную последовательность чисел; если сумма равна n , то n — совершенное тотиентное число.
Приложения
Циклотомия
В последнем разделе Disquisitiones [ 49] [50] Гаусс доказывает [51] , что правильный n -угольник может быть построен с помощью линейки и циркуля, если φ ( n ) является степенью 2. Если n является степенью нечетного простого числа, формула для тотиента гласит, что его тотиент может быть степенью 2, только если n является первой степенью, а n − 1 является степенью 2. Простые числа, которые на единицу больше степени 2, называются простыми числами Ферма , и известно всего пять из них: 3, 5, 17, 257 и 65537. Ферма и Гаусс знали о них. Никто не смог доказать, существуют ли еще какие-либо числа.
Таким образом, правильный n -угольник имеет конструкцию с помощью циркуля и линейки, если n является произведением различных простых чисел Ферма и любой степени числа 2. Первые несколько таких n равны [52]
- 2, 3, 4, 5, 6, 8, 10, 12, 15, 16, 17, 20, 24, 30, 32, 34, 40,... (последовательность A003401 в OEIS ).
Теорема о простых числах для арифметических прогрессий
Криптосистема RSA
Настройка системы RSA включает выбор больших простых чисел p и q , вычисление n = pq и k = φ ( n ) и нахождение двух чисел e и d таких, что ed ≡ 1 (mod k ) . Числа n и e («ключ шифрования») публикуются, а d («ключ дешифрования») хранится в тайне.
Сообщение, представленное целым числом m , где 0 < m < n , шифруется путем вычисления S = m e (mod n ) .
Он расшифровывается путем вычисления t = S d (mod n ) . Теорему Эйлера можно использовать, чтобы показать, что если 0 < t < n , то t = m .
Безопасность системы RSA была бы скомпрометирована, если бы число n можно было эффективно разложить на множители или если бы φ ( n ) можно было эффективно вычислить без разложения n .
Нерешенные проблемы
Гипотеза Лемера
Если p — простое число, то φ ( p ) = p − 1 . В 1932 году Д. Х. Лемер спросил, существуют ли составные числа n такие, что φ ( n ) делит n − 1 . Ни одно из них не известно. [53]
В 1933 году он доказал, что если существует такое n , то оно должно быть нечетным, свободным от квадратов и делиться по крайней мере на семь простых чисел (т. е. ω ( n ) ≥ 7 ). В 1980 году Коэн и Хагис доказали, что n > 10 20 и что ω ( n ) ≥ 14 . [54] Кроме того, Хагис показал, что если 3 делит n , то n > 10 1937042 и ω ( n ) ≥ 298848 . [55] [56]
Гипотеза Кармайкла
Это утверждает, что не существует числа n со свойством, что для всех других чисел m , m ≠ n , φ ( m ) ≠ φ ( n ) . См. теорему Форда выше.
Как указано в основной статье, если существует хотя бы один контрпример к этой гипотезе, то должно быть бесконечно много контрпримеров, и наименьший из них имеет не менее десяти миллиардов цифр в десятичной системе счисления. [40]
гипотеза Римана
Гипотеза Римана верна тогда и только тогда, когда неравенство
верно для всех n ≥ p 120569 # где γ — постоянная Эйлера , а p 120569 # — произведение первых 120569 простых чисел. [57]
Смотрите также
Примечания
- ^ "Эйлерова функция тотиента". Khan Academy . Получено 2016-02-26 .
- ^ Лонг (1972, стр. 85)
- ^ Петтофреццо и Биркит (1970, стр. 72)
- ^ Лонг (1972, стр. 162)
- ^ Петтофреццо и Биркит (1970, стр. 80)
- ^ См. теорему Эйлера.
- ↑ L. Euler "Theoremata arithmetica nova methodo demonstrata" (Арифметическая теорема, доказанная новым методом), Novi commentarii academiae scientiarum imperialis Petropolitanae (Новые записки Санкт-Петербургской Императорской Академии наук), 8 (1763), 74–104. (Работа была представлена в Санкт-Петербургской Академии 15 октября 1759 года. Работа с тем же названием была представлена в Берлинской Академии 8 июня 1758 года). Доступно в сети в: Ferdinand Rudio , ed. , Leonhardi Euleri Commentationes Arithmeticae , том 1, в: Leonhardi Euleri Opera Omnia , серия 1, том 2 (Лейпциг, Германия, BG Teubner, 1915), страницы 531–555. На странице 531 Эйлер определяет n как количество целых чисел, меньших N и взаимно простых с N (... aequalis sit multitudini numerorum ipso N minorum, qui simul ad eum sint primi, ...), что является фи-функцией φ(N).
- ^ ab Sandifer, стр. 203
- ^ Грэм и др., стр. 133, примечание 111.
- ^ Л. Эйлер, Speculationes circa quasdam insignes proprietates numerorum , Acta Academiae Scientarum Imperialis Petropolitinae, vol. 4, (1784), стр. 18–30, или Opera Omnia, серия 1, том 4, стр. 105–115. (Работа была представлена в Петербургской Академии 9 октября 1775 г.).
- ^ В литературе встречаются как φ ( n ), так и ϕ ( n ) . Это две формы строчной греческой буквы фи .
- ^ Гаусс, Disquisitiones Arithmeticae, статья 38
- ^ Каджори, Флориан (1929). История математических обозначений. Том II . Open Court Publishing Company. §409.
- ^ Дж. Дж. Сильвестр (1879) «О некоторых уравнениях тернарной кубической формы», American Journal of Mathematics , 2 : 357-393; Сильвестр вводит термин «totient» на странице 361.
- ^ "totient". Оксфордский словарь английского языка (2-е изд.). Oxford University Press . 1989.
- ^ Шрамм (2008)
- ^ Гаусс, DA, ст. 39
- ^ Гаусс, Д.А. ст. 39, ст. 52-54
- ^ Грэм и др., стр. 134-135.
- ^ ab Hardy & Wright 1979, том 328
- ^ Динева (во внешних ссылках), предложение 1
- ^ abc Уолфиш, Арнольд (1963). Экспоненциальные суммы Вейля в neueren Zahlentheorie . Mathematische Forschungsberichte (на немецком языке). Том. 16. Берлин: VEB Deutscher Verlag der Wissenschaften . Збл 0146.06003.
- ^ Ломадсе, Г. (1964), «Научная работа Арнольда Вальфиса» (PDF) , Acta Arithmetica , 10 (3): 227– 237, doi :10.4064/aa-10-3-227-237
- ^ ab Sitaramachandrarao, R. (1985). «Об ошибке члена Ландау II». Rocky Mountain J. Math . 15 (2): 579– 588. doi : 10.1216/RMJ-1985-15-2-579 .
- ^ Поллак, П. (2023), «Две проблемы распределения лямбда-функции Кармайкла», Mathematika , 69 (4): 1195– 1220, arXiv : 2303.14043 , doi : 10.1112/mtk.12222
- ↑ Харди и Райт 1979, том 288.
- ↑ Харди и Райт 1979, том 309.
- ↑ Харди и Райт 1979, введение к § 18.4.
- ^ Харди и Райт 1979, том 326
- ↑ Харди и Райт 1979, том 327.
- ^ Фактически, теорема Чебышева (Hardy & Wright 1979, thm.7) и третья теорема Мертенса — это все, что нужно.
- ↑ Харди и Райт 1979, том 436.
- ↑ Теорема 15 Россера, Дж. Баркли; Шенфельда, Лоуэлла (1962). «Приближенные формулы для некоторых функций простых чисел». Illinois J. Math . 6 (1): 64– 94. doi : 10.1215/ijm/1255631807 .
- ^ Бах и Шаллит, том 8.8.7
- ^ ab Ribenboim (1989). «Как распределены простые числа? §IC Распределение значений функции Эйлера». Книга рекордов простых чисел (2-е изд.). Нью-Йорк: Springer-Verlag. С. 172– 175. doi :10.1007/978-1-4684-0507-1_5. ISBN 978-1-4684-0509-5.
- ^ Шандор, Митринович и Крстичи (2006), стр. 24–25.
- ↑ Харди и Райт 1979, том 332.
- ^ abc Рибенбойм, стр.38
- ^ аб Шандор, Митринович и Крстичи (2006), стр.16
- ^ ab Guy (2004) стр.144
- ^ Шандор и Крстичи (2004) стр.230
- ^ Чжан, Минчжи (1993). «О не-тотиентах». Журнал теории чисел . 43 (2): 168– 172. doi : 10.1006/jnth.1993.1014 . ISSN 0022-314X. Zbl 0772.11001.
- ^ abc Ford, Kevin (1998). «Распределение тотиентов». Ramanujan J . 2 ( 1– 2): 67– 151. doi :10.1023/A:1009761909132. ISSN 1382-4090. Zbl 0914.11053.Перепечатано в Analytic and Elementary Number Theory: A Tribute to Mathematical Legend Paul Erdos , Developments in Mathematics, т. 1, 1998, doi :10.1007/978-1-4757-4507-8_8, ISBN 978-1-4419-5058-1 . Обновлено и исправлено в arXiv :1104.3264, 2011.
- ^ Шандор и др. (2006) стр.22
- ^ Шандор и др. (2006) стр.21
- ^ ab Guy (2004) стр.145
- ^ Шандор и Крстичи (2004) стр.229
- ^ Шандор и Крстичи (2004) стр.228
- ^ Гаусс, ДА. 7-й § — это статьи 336–366.
- ^ Гаусс доказал, что если n удовлетворяет определенным условиям, то n -угольник может быть построен. В 1837 году Пьер Ванцель доказал обратное: если n -угольник конструируем, то n должно удовлетворять условиям Гаусса
- ^ Гаусс, DA, ст. 366
- ^ Гаусс, DA, ст. 366. Этот список является последним предложением в Disquisitiones
- ↑ Рибенбойм, стр. 36–37.
- ^ Коэн, Грэм Л.; Хагис, Питер младший (1980). «О количестве простых делителей числа n , если φ ( n ) делит n − 1 ». Нью-Арк. Вискд . III серия. 28 : 177–185 . ISSN 0028-9825. Збл 0436.10002.
- ^ Хагис, Питер младший (1988). «Об уравнении M ·φ( n ) = n − 1 ». Нью-Арк. Вискд . IV серия. 6 (3): 255–261 . ISSN 0028-9825. Збл 0668.10006.
- ^ Гай (2004) стр.142
- ^ Броган, Кевин (2017). Эквиваленты гипотезы Римана, том первый: арифметические эквиваленты (первое издание). Cambridge University Press. ISBN 978-1-107-19704-6.Следствие 5.35
Ссылки
Disquisitiones Arithmeticae переведены с латыни на английский и немецкий языки. Немецкое издание включает все работы Гаусса по теории чисел: все доказательства квадратичной взаимности, определение знака суммы Гаусса, исследования биквадратичной взаимности и неопубликованные заметки.
Ссылки на Disquisitiones имеют форму Gauss, DA, art. nnn .
- Абрамовиц, М.; Стиган , И.А. (1964), Справочник по математическим функциям, Нью-Йорк: Dover Publications , ISBN 0-486-61272-4. См. пункт 24.3.2.
- Бах, Эрик ; Шаллит, Джеффри (1996), Алгоритмическая теория чисел (Том I: Эффективные алгоритмы) , Серия издательства MIT Press по основам вычислений, Кембридж, Массачусетс: Издательство MIT Press , ISBN 0-262-02405-5, ЗБЛ 0873.11070
- Диксон, Леонард Юджин, «История теории чисел», том 1, глава 5 «Функция Эйлера, обобщения; ряды Фарея», Chelsea Publishing 1952
- Форд, Кевин (1999), «Число решений φ( x ) = m », Annals of Mathematics , 150 (1): 283– 311, doi :10.2307/121103, ISSN 0003-486X, JSTOR 121103, MR 1715326, Zbl 0978.11053.
- Гаусс, Карл Фридрих (1986), Disquisitiones Arithmeticae (второе, исправленное издание) , перевод Кларка, Артура А., Нью-Йорк: Springer , ISBN 0-387-96254-9
- Гаусс, Карл Фридрих (1965), «Рассуждения об арифметике и другие работы по теории чисел» (Второе издание) , перевод Мазера, Х., Нью-Йорк: Челси, ISBN 0-8284-0191-8
- Грэм, Рональд ; Кнут, Дональд ; Паташник, Орен (1994), Конкретная математика : основа компьютерной науки (2-е изд.), Рединг, Массачусетс: Addison-Wesley, ISBN 0-201-55802-5, ЗБЛ 0836.00001
- Гай, Ричард К. (2004), Нерешенные проблемы теории чисел , Сборник задач по математике (3-е изд.), Нью-Йорк, штат Нью-Йорк: Springer-Verlag , ISBN 0-387-20860-7, Збл 1058.11001
- Харди, Г. Х.; Райт , Э. М. (1979), Введение в теорию чисел (пятое изд.), Оксфорд: Oxford University Press , ISBN 978-0-19-853171-5
- Лю, Х.-К. (2016), «О функции Эйлера», Proc. Roy. Soc. Edinburgh Sect. A , 146 (4): 769– 775, doi :10.1017/S0308210515000682.
- Лонг, Кэлвин Т. (1972), Элементарное введение в теорию чисел (2-е изд.), Лексингтон: DC Heath and Company , LCCN 77-171950
- Петтофреццо, Энтони Дж.; Биркит, Дональд Р. (1970), Элементы теории чисел , Englewood Cliffs: Prentice Hall , LCCN 77-81766
- Рибенбойм, Пауло (1996), Новая книга рекордов простых чисел (3-е изд.), Нью-Йорк: Springer , ISBN 0-387-94457-5, ЗБЛ 0856.11001
- Сэндифер, Чарльз (2007), Ранняя математика Леонарда Эйлера , MAA, ISBN 978-0-88385-559-1
- Шандор, Йожеф; Митринович, Драгослав С.; Крстичи, Борислав, ред. (2006), Справочник по теории чисел I , Дордрехт: Springer-Verlag , стр. 9–36 , ISBN 1-4020-4215-9, Збл 1151.11300
- Шандор, Йожеф; Крстичи, Борислав (2004). Справочник по теории чисел II . Дордрехт: Клювер Академик. стр. 179–327. ISBN 1-4020-2546-7. Збл 1079.11001.
- Шрамм, Вольфганг (2008), «Преобразование Фурье функций наибольшего общего делителя», Электронный журнал комбинаторной теории чисел , A50 (8(1)).
Внешние ссылки
- "Функция Totient", Энциклопедия математики , EMS Press , 2001 [1994]
- Фи-функция Эйлера и китайская теорема об остатках — доказательство того, что φ(n) мультипликативна. Архивировано 28.02.2021 на Wayback Machine
- Калькулятор функции тотиента Эйлера на JavaScript — до 20 цифр
- Динева, Росица, Эйлеров тотиент, Мёбиус и функции делителей Архивировано 2021-01-16 на Wayback Machine
- Плитадж, Лумис, Полхилл подводят итоги по функции Эйлера Фи










![{\displaystyle {\begin{array}{rcl}\varphi (n)&=&\varphi (p_{1}^{k_{1}})\,\varphi (p_{2}^{k_{2}})\cdots \varphi (p_{r}^{k_{r}})\\[.1em]&=&p_{1}^{k_{1}}\left(1-{\frac {1}{p_{1}}}\right)p_{2}^{k_{2}}\left(1-{\frac {1}{p_{2}}}\right)\cdots p_{r}^{k_{r}}\left(1-{\frac {1}{p_{r}}}\right)\\[.1em]&=&p_{1}^{k_{1}}p_{2}^{k_{2}}\cdots p_{r}^{k_{r}}\left(1-{\frac {1}{p_{1}}}\right)\left(1-{\frac {1}{p_{2}}}\right)\cdots \left(1-{\frac {1}{p_{r}}}\right)\\[.1em]&=&n\left(1-{\frac {1}{p_{1}}}\right)\left(1-{\frac {1}{p_{2}}}\right)\cdots \left(1-{\frac {1}{p_{r}}}\right).\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f7447918f84f4509322dda0b4aa4384ab8072a93)



![{\displaystyle {\mathcal {F}}\{\mathbf {x} \}[m]=\sum \limits _{k=1}^{n}x_{k}\cdot e^{{-2\pi i}{\frac {mk}{n}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/44406da8bf27ff396599d35e91d4328c3f961a81)
![{\displaystyle \varphi (n)={\mathcal {F}}\{\mathbf {x} \}[1]=\sum \limits _{k=1}^{n}\gcd(k,n)e^{-2\pi i{\frac {k}{n}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1a88a09856ce4f73559b80fb01e44bdd70af8309)












![{\displaystyle {\begin{align}\varphi (20)&=\mu (1)\cdot 20+\mu (2)\cdot 10+\mu (4)\cdot 5+\mu (5)\cdot 4+\mu (10)\cdot 2+\mu (20)\cdot 1\\[.5em]&=1\cdot 20-1\cdot 10+0\cdot 5-1\cdot 4+1\cdot 2+0\cdot 1=8.\end{align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5a4ce2d54734e410d4eea1d1a6b0d62ad7fbfed9)




































![{\displaystyle {\begin{align}\lim \inf {\frac {\varphi (n+1)}{\varphi (n)}}&=0\quad {\text{and}}\\[5px]\lim \sup {\frac {\varphi (n+1)}{\varphi (n)}}&=\infty .\end{align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc005e44784aa197220263d20f9a495ee655b528)




