Удлиненная пятиугольная бипирамида
| Удлиненная пятиугольная бипирамида | |
|---|---|
 | |
| Тип | Джонсон Дж 15 – Дж 16 – Дж 17 |
| Лица | 10 треугольников 5 квадратов |
| Края | 25 |
| Вершины | 12 |
| Конфигурация вершины | 10(3 2 .4 2 ) 2(3 5 ) |
| Группа симметрии | Д 5ч , [5,2], (*522) |
| Группа вращения | Д 5 , [5,2] + , (522) |
| Двойной многогранник | Пятиугольный бифрустум |
| Характеристики | выпуклый |
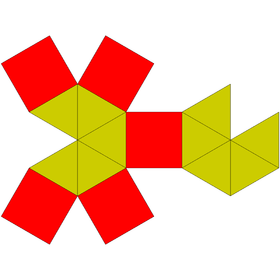
| Сеть | |
 | |
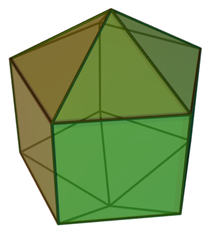
В геометрии вытянутая пентагональная бипирамида — многогранник, образованный присоединением двух пентагональных пирамид к основанию пятиугольной призмы . Это пример тела Джонсона .
Строительство
Вытянутая пятиугольная бипирамида построена из пятиугольной призмы путем присоединения двух пятиугольных пирамид к ее основаниям, процесс называется удлинением . Эти пирамиды покрывают пятиугольные грани так, что полученный многогранник состоит из десяти равносторонних треугольников и пяти квадратов . [1] [2] Выпуклый многогранник, в котором все грани являются правильными многоугольниками, называется телом Джонсона . Вытянутая пятиугольная бипирамида входит в их число и называется шестнадцатым телом Джонсона . [3]
Характеристики
Площадь поверхности вытянутой пятиугольной бипирамиды равна сумме площадей всех многоугольных граней: десяти равносторонних треугольников и пяти квадратов. Ее объем можно определить, разбив ее на две пятиугольные пирамиды и одну правильную пятиугольную призму, а затем сложив ее объем. Для вытянутой пятиугольной бипирамиды с длиной ребра их можно сформулировать как: [2]
Она имеет ту же трехмерную группу симметрии, что и пятиугольная призма, двугранную группу порядка 20. Ее двугранный угол можно вычислить, сложив угол пятиугольной пирамиды и пятиугольной призмы: [4]
- двугранный угол вытянутой пятиугольной бипирамиды между двумя соседними треугольными гранями равен углу пятиугольной пирамиды между ними, т. е. 138,19°.
- двугранный угол вытянутой пятиугольной бипирамиды между двумя соседними квадратными гранями равен углу правильной пятиугольной призмы, внутренний угол правильного пятиугольника — 108°.
- двугранный угол вытянутой пятиугольной бипирамиды между квадратом и треугольником равен сумме двугранного угла пятиугольной пирамиды между треугольником и пятиугольником и двугранного угла пятиугольной призмы между квадратом и пятиугольником, 37,38° + 90° = 127,38°.
Двойственной к вытянутой квадратной бипирамиде является пятиугольный бифрустум .
Ссылки
- ^ Раджваде, AR (2001), Выпуклые многогранники с условиями регулярности и третья проблема Гильберта, Тексты и чтения по математике, Hindustan Book Agency, doi :10.1007/978-93-86279-06-4, ISBN 978-93-86279-06-4.
- ^ ab Берман, Мартин (1971), «Выпуклые многогранники с правильными гранями», Журнал Института Франклина , 291 (5): 329–352 , doi :10.1016/0016-0032(71)90071-8, MR 0290245.
- ^ Фрэнсис, Даррил (август 2013 г.), «Твердые тела Джонсона и их аббревиатуры», Word Ways , 46 (3): 177.
- ^ Джонсон, Норман В. (1966), «Выпуклые многогранники с правильными гранями», Канадский журнал математики , 18 : 169–200 , doi : 10.4153/cjm-1966-021-8 , MR 0185507, S2CID 122006114, Zbl 0132.14603.
Внешние ссылки
- Вайсштейн, Эрик В. , «Удлиненная пентагональная бипирамида» («тело Джонсона») на MathWorld .
 | Эта статья о многогранниках — заглушка . Вы можете помочь Википедии, расширив ее. |
