Оптическое вращение

- Источник света
- Неполяризованный свет
- Линейный поляризатор
- Линейно поляризованный свет
- Пробирка с образцом, содержащая исследуемые молекулы
- Оптическое вращение, вызванное молекулами
- Вращающийся линейный анализатор
- Детектор
Оптическое вращение , также известное как поляризационное вращение или круговое двупреломление , представляет собой вращение ориентации плоскости поляризации вокруг оптической оси линейно поляризованного света при его прохождении через определенные материалы. Круговое двупреломление и круговой дихроизм являются проявлениями оптической активности . Оптическая активность возникает только в хиральных материалах, в которых отсутствует микроскопическая зеркальная симметрия. В отличие от других источников двупреломления , которые изменяют состояние поляризации луча, оптическую активность можно наблюдать в жидкостях . Это может включать газы или растворы хиральных молекул, таких как сахара, молекулы со спиральной вторичной структурой, такие как некоторые белки, а также хиральные жидкие кристаллы . Ее также можно наблюдать в хиральных твердых телах, таких как определенные кристаллы с вращением между соседними кристаллическими плоскостями (например, кварц ) или метаматериалах .
Если смотреть на источник света, вращение плоскости поляризации может быть либо правым ( правовращающим или правовращающим — d -вращательным, обозначенным (+), по часовой стрелке), либо левым ( левовращающим или левовращающим — l -вращательным, обозначенным (−), против часовой стрелки) в зависимости от того, какой стереоизомер доминирует. Например, сахароза и камфара являются d -вращательными, тогда как холестерин является l -вращательным. Для данного вещества угол, на который поворачивается поляризация света определенной длины волны, пропорционален длине пути через материал и (для раствора) пропорционален его концентрации.
Оптическая активность измеряется с помощью поляризованного источника и поляриметра . Это инструмент, который в частности используется в сахарной промышленности для измерения концентрации сахара в сиропе, и в целом в химии для измерения концентрации или энантиомерного отношения хиральных молекул в растворе. Модуляция оптической активности жидкого кристалла, наблюдаемая между двумя листовыми поляризаторами , является принципом работы жидкокристаллических дисплеев (используемых в большинстве современных телевизоров и компьютерных мониторов).
Формы
Правое вращение и левое вращение (также пишется как левовращающее ) [1] [2] в химии и физике — это оптическое вращение плоскополяризованного света . С точки зрения наблюдателя правое вращение относится к вращению по часовой стрелке или вправо, а левое вращение относится к вращению против часовой стрелки или влево. [3] [4]
Химическое соединение , вызывающее правое вращение, называется правовращающим или правовращающим , в то время как соединение, вызывающее левовращающее, называется левовращающим или левовращающим . [5] Соединения с такими свойствами состоят из хиральных молекул и, как говорят, обладают оптической активностью. Если хиральная молекула правовращающая, ее энантиомер (геометрическое зеркальное изображение) будет левовращающим, и наоборот. Энантиомеры вращают плоскополяризованный свет на одинаковое число градусов, но в противоположных направлениях.
Префиксы хиральности
Соединение может быть помечено как правовращающее с помощью префикса "(+)-" или " d- ". Аналогично, левовращающее соединение может быть помечено с помощью префикса "(−)-" или " l- ". Строчные префиксы " d- " и " l- " устарели и отличаются от МАЛЫХ ЗАГЛАВНЫХ префиксов " D- " и " L- ". Префиксы " D- " и " L- " используются для указания энантиомера хиральных органических соединений в биохимии и основаны на абсолютной конфигурации соединения относительно (+)- глицеральдегида , который по определению является D -формой. Префикс, используемый для указания абсолютной конфигурации, не связан напрямую с префиксом (+) или (−), используемым для указания оптического вращения в той же молекуле. Например, девять из девятнадцати L - аминокислот, встречающихся в природе в белках, несмотря на префикс L- , на самом деле являются правовращающими (при длине волны 589 нм), а D - фруктозу иногда называют «левулозой», потому что она левовращающая.
Префиксы D - и L - описывают молекулу в целом, как и префиксы (+) и (−) для оптического вращения. Напротив, префиксы ( R )- и ( S )- из правил приоритета Кана–Ингольда–Прелога характеризуют абсолютную конфигурацию каждого конкретного хирального стереоцентра с молекулой, а не свойство молекулы в целом. Молекула, имеющая ровно один хиральный стереоцентр (обычно асимметричный атом углерода ), может быть обозначена ( R ) или ( S ), но молекула, имеющая несколько стереоцентров, нуждается в более чем одной метке. Например, незаменимая аминокислота L -треонин содержит два хиральных стереоцентра и записывается как (2 S ,3 S )-треонин. Строгой связи между обозначениями R/S, D / L и (+)/(−) нет , хотя некоторые корреляции существуют. Например, из встречающихся в природе аминокислот все являются L , а большинство являются ( S ). Для некоторых молекул ( R )-энантиомер является правовращающим (+) энантиомером, а в других случаях это левовращающий (−) энантиомер. Соотношение должно определяться в каждом конкретном случае экспериментальными измерениями или детальным компьютерным моделированием. [6]
История
.jpg/440px-Sucrose_solution_and_polaroid_(optical_activity).jpg)
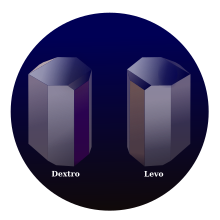
Вращение ориентации линейно поляризованного света было впервые обнаружено в 1811 году в кварце французским физиком Франсуа Араго . [7] В 1820 году английский астроном сэр Джон Ф. У. Гершель обнаружил, что различные отдельные кристаллы кварца, кристаллические структуры которых являются зеркальными отражениями друг друга (см. иллюстрацию), вращают линейную поляризацию на одинаковую величину, но в противоположных направлениях. [8] Жан Батист Био также наблюдал вращение оси поляризации в некоторых жидкостях [9] и парах органических веществ, таких как скипидар . [10] В 1822 году Огюстен Жан Френель обнаружил, что оптическое вращение можно объяснить как разновидность двойного лучепреломления : в то время как ранее известные случаи двойного лучепреломления были обусловлены разными скоростями света, поляризованного в двух перпендикулярных плоскостях, оптическое вращение было обусловлено разными скоростями правого и левого кругово поляризованного света. [11] С тех пор для измерения концентрации простых сахаров, таких как глюкоза , в растворе использовались простые поляриметры . Фактически одно из названий D -глюкозы (биологического изомера) — декстроза , что связано с тем, что она заставляет линейно поляризованный свет вращаться в правую или правую сторону. Аналогичным образом левулоза, более известная как фруктоза , заставляет плоскость поляризации вращаться влево. Фруктоза еще более левовращающая, чем глюкоза правовращающая. Инвертный сахарный сироп , коммерчески получаемый путем гидролиза сахарозного сиропа до смеси компонентов простых сахаров, фруктозы и глюкозы, получил свое название из-за того , что преобразование заставляет направление вращения «инвертироваться» справа налево.
В 1849 году Луи Пастер решил проблему, касающуюся природы винной кислоты . [12] Раствор этого соединения, полученного из живых существ (точнее, винный осадок ), вращает плоскость поляризации проходящего через него света, но винная кислота, полученная путем химического синтеза, не имеет такого эффекта, хотя ее реакции идентичны и ее элементный состав одинаков. Пастер заметил, что кристаллы бывают двух асимметричных форм, которые являются зеркальными отражениями друг друга. Сортировка кристаллов вручную дала две формы соединения: Растворы одной формы вращают поляризованный свет по часовой стрелке, в то время как другая форма вращает свет против часовой стрелки. Равная смесь этих двух не оказывает поляризующего эффекта на свет. Пастер пришел к выводу, что рассматриваемая молекула асимметрична и может существовать в двух различных формах, которые похожи друг на друга, как перчатки для левой и правой руки, и что органическая форма соединения состоит исключительно из одного типа.
В 1874 году Якобус Хенрикус ван 'т Хофф [13] и Жозеф Ахилл Ле Бель [14] независимо друг от друга предположили, что это явление оптической активности в углеродных соединениях можно объяснить, предположив, что 4 насыщенные химические связи между атомами углерода и их соседями направлены к углам правильного тетраэдра. Если все 4 соседа различны, то существует два возможных порядка соседей вокруг тетраэдра, которые будут зеркальными отражениями друг друга. Это привело к лучшему пониманию трехмерной природы молекул.
В 1945 году Чарльз Уильям Банн [15] предсказал оптическую активность ахиральных структур, если направление распространения волны и ахиральная структура образуют экспериментальную установку, отличную от ее зеркального отображения. Такая оптическая активность, обусловленная внешней хиральностью, наблюдалась в 1960-х годах в жидких кристаллах. [16] [17]
В 1950 году Сергей Вавилов [18] предсказал оптическую активность, зависящую от интенсивности света, а эффект нелинейной оптической активности наблюдался в 1979 году в кристаллах иодата лития . [19]
Оптическая активность обычно наблюдается для проходящего света. Однако в 1988 году М. П. Сильверман обнаружил, что вращение поляризации может происходить и для света, отраженного от хиральных веществ. [20] Вскоре после этого было замечено, что хиральные среды могут также отражать лево- и правовращающие круговые поляризованные волны с различной эффективностью. [21] Эти явления зеркального кругового двойного лучепреломления и зеркального кругового дихроизма совместно известны как зеркальная оптическая активность. Зеркальная оптическая активность очень слаба в природных материалах.
В 1898 году Джагадиш Чандра Бозе описал способность скрученных искусственных структур вращать поляризацию микроволн . [22] С начала 21-го века развитие искусственных материалов привело к предсказанию [23] и реализации [24] [25] хиральных метаматериалов с оптической активностью, превышающей на порядки величину естественную среду в оптической части спектра. Было обнаружено, что внешняя хиральность, связанная с косым освещением метаповерхностей, лишенных двукратной вращательной симметрии, приводит к большой линейной оптической активности при пропускании [26] и отражении, [27], а также к нелинейной оптической активности, превышающей активность иодата лития в 30 миллионов раз. [28]
Теория
Оптическая активность возникает из-за молекул, растворенных в жидкости, или из-за самой жидкости, только если молекулы являются одним из двух (или более) стереоизомеров ; это известно как энантиомер . Структура такой молекулы такова, что она не идентична своему зеркальному отображению (которое было бы отражением другого стереоизомера или «противоположного энантиомера»). В математике это свойство также известно как хиральность . Например, металлический стержень не является хиральным, поскольку его вид в зеркале не отличается от него самого. Однако винт или основание лампочки (или любой вид спирали ) являются хиральными; обычная правая резьба винта, рассматриваемая в зеркале, будет выглядеть как левая резьба (очень редко), которая, возможно, не сможет ввинтиться в обычную (правую) гайку. У человека, рассматриваемого в зеркале, сердце будет с правой стороны, явное доказательство хиральности, в то время как зеркальное отражение куклы вполне может быть неотличимо от самой куклы.
Для того чтобы проявить оптическую активность, жидкость должна содержать только один или преобладание одного стереоизомера. Если два энантиомера присутствуют в равных пропорциях, то их эффекты нейтрализуются, и оптическая активность не наблюдается; это называется рацемической смесью. Но когда есть энантиомерный избыток , больше одного энантиомера, чем другого, нейтрализация неполная, и оптическая активность наблюдается. Многие встречающиеся в природе молекулы присутствуют только в виде одного энантиомера (например, многие сахара). Хиральные молекулы, полученные в областях органической химии или неорганической химии, являются рацемическими, если только в той же реакции не использовался хиральный реагент.
На фундаментальном уровне вращение поляризации в оптически активной среде вызвано круговым двупреломлением и может быть лучше всего понято таким образом. В то время как линейное двупреломление в кристалле подразумевает небольшую разницу в фазовой скорости света двух различных линейных поляризаций, круговое двупреломление подразумевает небольшую разницу в скоростях между правой и левой круговыми поляризациями . [11] Представьте себе один энантиомер в растворе как большое количество маленьких спиралей (или винтов), все правосторонние, но в случайных ориентациях. Двупреломление такого рода возможно даже в жидкости, поскольку направленность спиралей не зависит от их ориентации: даже когда направление одной спирали меняется на противоположное, она все равно кажется правосторонней. И сам по себе циркулярно поляризованный свет является хиральным: когда волна движется в одном направлении, электрические (и магнитные) поля, составляющие ее, вращаются по часовой стрелке (или против часовой стрелки для противоположной круговой поляризации), вычерчивая в пространстве правый (или левый) винтовой узор. В дополнение к объемному показателю преломления , который существенно снижает фазовую скорость света в любом диэлектрическом (прозрачном) материале по сравнению со скоростью света (в вакууме), существует дополнительное взаимодействие между хиральностью волны и хиральностью молекул. Там, где их хиральности одинаковы, будет небольшой дополнительный эффект на скорость волны, но противоположная круговая поляризация будет испытывать противоположный небольшой эффект, поскольку ее хиральность противоположна хиральности молекул.
Однако в отличие от линейного двулучепреломления естественное оптическое вращение (при отсутствии магнитного поля) не может быть объяснено в терминах локального тензора диэлектрической проницаемости материала (т. е. зарядового отклика, который зависит только от локального вектора электрического поля), поскольку соображения симметрии запрещают это. Скорее, круговое двулучепреломление появляется только при рассмотрении нелокальности материального отклика, явления, известного как пространственная дисперсия . [29] Нелокальность означает, что электрические поля в одном месте материала управляют токами в другом месте материала. Свет распространяется с конечной скоростью, и хотя он намного быстрее электронов, имеет значение, хочет ли зарядовый отклик естественным образом перемещаться вместе с электромагнитным волновым фронтом или противоположно ему. Пространственная дисперсия означает, что свет, распространяющийся в разных направлениях (разные волновые векторы), видит немного другой тензор диэлектрической проницаемости. Естественное оптическое вращение требует специального материала, но оно также опирается на тот факт, что волновой вектор света не равен нулю, а ненулевой волновой вектор обходит ограничения симметрии локального (нулевого волнового вектора) отклика. Однако все еще существует инверсная симметрия, поэтому направление естественного оптического вращения должно быть «обратным», когда направление света меняется на противоположное, в отличие от магнитного вращения Фарадея . Все оптические явления имеют некоторое влияние нелокальности/волнового вектора, но оно обычно пренебрежимо мало; естественное оптическое вращение, что довольно уникально, абсолютно требует этого. [29]
Фазовая скорость света в среде обычно выражается с помощью показателя преломления n , определяемого как скорость света (в свободном пространстве), деленная на его скорость в среде. Разница в показателях преломления между двумя круговыми поляризациями количественно определяет силу кругового двойного лучепреломления (вращение поляризации),
- .
Хотя в природных материалах он невелик, для хиральных метаматериалов были зарегистрированы примеры гигантского кругового двойного лучепреломления, приводящего к отрицательному показателю преломления для одной круговой поляризации. [30] [31]
Знакомое вращение оси линейной поляризации основано на понимании того, что линейно поляризованная волна может быть описана как суперпозиция ( сложение) левой и правой циркулярно поляризованной волны в равной пропорции. Разность фаз между этими двумя волнами зависит от ориентации линейной поляризации, которую мы будем называть , а их электрические поля имеют относительную разность фаз, которая затем складывается, чтобы создать линейную поляризацию:
где - электрическое поле чистой волны, а и - две циркулярно поляризованные базисные функции (имеющие нулевую разность фаз). Предполагая распространение в направлении +z , мы могли бы записать и в терминах их x- и y -компонент следующим образом:
где и являются единичными векторами, а i является мнимой единицей , в данном случае представляющей сдвиг фазы на 90 градусов между компонентами x и y , на которые мы разложили каждую круговую поляризацию. Как обычно, когда имеешь дело с векторной записью, подразумевается, что такие величины должны быть умножены на , а затем фактическое электрическое поле в любой момент времени задается действительной частью этого произведения.
Подставляя эти выражения для и в уравнение для получаем:
Последнее уравнение показывает, что результирующий вектор имеет компоненты x и y в фазе и ориентирован точно в том направлении, как мы и предполагали, оправдывая представление любого линейно поляризованного состояния под углом как суперпозиции правого и левого кругово поляризованных компонентов с относительной разностью фаз . Теперь предположим передачу через оптически активный материал, который вызывает дополнительную разность фаз между правыми и левыми кругово поляризованными волнами . Назовем результат прохождения исходной волны линейно поляризованной под углом через эту среду. Это применит дополнительные фазовые множители и к правому и левому кругово поляризованным компонентам :
Используя аналогичную математику, как указано выше, находим:
таким образом, описывая волну, линейно поляризованную под углом , и, таким образом, повернутую относительно входящей волны:
Выше мы определили разницу в показателях преломления для право- и левополяризованных круговых волн . Рассматривая распространение на длину L в таком материале, между ними возникнет дополнительная разность фаз (как мы использовали выше), определяемая как:
- ,
где - длина волны света (в вакууме). Это вызовет поворот линейной оси поляризации на величину, как мы показали.
В общем случае показатель преломления зависит от длины волны (см. дисперсия ), а дифференциальный показатель преломления также будет зависеть от длины волны. Результирующее изменение вращения в зависимости от длины волны света называется оптической вращательной дисперсией (ОВД). Спектры ОВД и спектры кругового дихроизма связаны соотношениями Крамерса–Кронига . Полное знание одного спектра позволяет рассчитать другой.
Таким образом, мы обнаруживаем, что степень вращения зависит от цвета света (для измерений обычно используется желтая линия натрия D с длиной волны около 589 нм ) и прямо пропорциональна длине пути через вещество и величине кругового двупреломления материала , которая для раствора может быть вычислена из удельного вращения вещества и его концентрации в растворе.
Хотя оптическая активность обычно считается свойством жидкостей, особенно водных растворов , она также наблюдалась в кристаллах, таких как кварц (SiO 2 ). Хотя кварц имеет существенное линейное двупреломление, этот эффект отменяется, когда распространение происходит вдоль оптической оси . В этом случае вращение плоскости поляризации наблюдается из-за относительного вращения между кристаллическими плоскостями, таким образом делая кристалл формально хиральным, как мы определили его выше. Вращение кристаллических плоскостей может быть правым или левым, снова производя противоположные оптические активности. С другой стороны, аморфные формы кремнезема , такие как плавленый кварц , подобно рацемической смеси хиральных молекул, не имеют чистой оптической активности, поскольку та или иная кристаллическая структура не доминирует над внутренней молекулярной структурой вещества.
Приложения
Для чистого вещества в растворе, если цвет и длина пути фиксированы, а удельное вращение известно, наблюдаемое вращение можно использовать для расчета концентрации. Такое использование делает поляриметр инструментом большой важности для тех, кто торгует или использует сахарные сиропы оптом.
Сравнение с эффектом Фарадея
Вращение плоскости поляризации света может также происходить через эффект Фарадея , который включает статическое магнитное поле . Однако это отдельное явление, которое не классифицируется как «оптическая активность». Оптическая активность является взаимной, т. е. она одинакова для противоположных направлений распространения волны через оптически активную среду, например, вращение поляризации по часовой стрелке с точки зрения наблюдателя. В случае оптически активных изотропных сред вращение одинаково для любого направления распространения волны. Напротив, эффект Фарадея является невзаимным, т. е. противоположные направления распространения волны через среду Фарадея приведут к вращению поляризации по часовой стрелке и против часовой стрелки с точки зрения наблюдателя. Вращение Фарадея зависит от направления распространения относительно направления приложенного магнитного поля. Все соединения могут демонстрировать вращение поляризации в присутствии приложенного магнитного поля, при условии, что (компонент) магнитного поля ориентирован в направлении распространения света. Эффект Фарадея — одно из первых открытий взаимосвязи света и электромагнитных эффектов.
Смотрите также
Ссылки
- ^ Первый компонент слова dextro- происходит от латинского слова dexter , означающего «правый» (в отличие от левого). Laevo- или levo- происходит от латинского laevus , означающего «левая сторона».
- ^ Эквивалентные французские термины — dextrogyre и lévogyre. Они нечасто используются в английском языке, но иногда встречаются, см., например, Patrick Mailliet et al., стр. 12 и 15.
- ^ LibreTexts Химия – Поляриметрия
- ^ «Определение оптического вращения и удельного вращения». Международная фармакопея (11-е изд.). Всемирная организация здравоохранения. 2022.
- ^ Соломонс, TW Graham; Фрайл, Graig B. (2008). Органическая химия (9-е изд.). Хобокен: John Wiley & Sons, Inc. стр. 195. ISBN 9780471684961.
- ^ См., например, Stephens, PJ; Devlin, FJ; Cheeseman, JR; Frisch, MJ; Bortolini, O.; Besse, P. (2003). «Определение абсолютной конфигурации с использованием расчета оптического вращения». Хиральность . 15 : S57–64. doi :10.1002/chir.10270. PMID 12884375.
- ^ Араго (1811) «Mémoire sur unemodification remarquable qu'éprouvent les rayons lumineux dans leur pass à travers somes corpsdiaphanes et sur quelques autres nouveaux phénomènes d'optique» (Мемуары о замечательной модификации, которую световые лучи испытывают во время прохождения через определенные полупрозрачных веществах и о некоторых других новых оптических явлениях), «Mémoires de la класс математических и физических наук Имперского института Франции , 1-я часть: 93–134.
- ↑ Гершель, Дж. Ф. У. (1820) «О вращении, производимом пластинами горного хрусталя на плоскости поляризации лучей света, в связи с некоторыми особенностями его кристаллизации», Труды Кембриджского философского общества , 1 : 43–51.
- ^ Био, Ж.Б. (1815) «Феномен последовательной поляризации, наблюдаемый в однородных жидкостях» (Феномен последовательной поляризации, наблюдаемый в однородных жидкостях), Bulletin des Sciences, par la Société Philomatique de Paris , 190–192.
- ↑ Био (1818 и 1819) «Extrait d'un mémoire sur les вращений, которые некоторые вещества наносят на оси поляризации лучей света» (Отрывок из мемуаров о [оптических] вращениях, которые некоторые вещества оказывают на оси поляризации света лучи), Annales de Chimie et de Physique , 2-я серия, 9 : 372–389; 10 : 63–81; об опытах Био с парами скипидара ( vapeur d'essence de térébenthine ) см. стр. 72–81.
- ^ аб А. Френель, «Mémoire sur la double refraction que les lumineux éprouvent en traversant les aiguilles de cristal de roche suivant les Directions parallèles à l'axe», прочитано 9 декабря 1822 года; напечатано в журналах Х. де Сенармона, Э. Верде и Л. Френеля (ред.), Oeuvres complètes d'Augustin Fresnel , vol. 1 (1866), стр. 731–751; переведено как «Мемуары о двойном преломлении, которому подвергаются лучи света при прохождении игл кварца в направлениях, параллельных оси», Зенодо : 4745976 , 2021 (открытый доступ); особенно §13.
- ^ Пастер, Л. (1850) «Recherches sur les propriétés spécifiques des deux acides qui composent l'acide racémique» (Исследования специфических свойств двух кислот, составляющих рацемовую кислоту), Annales de chimie et de Physique , 3-я серия , 28 : 56–99; см. также приложение, стр. 99–117.
- ^ ван 'т Хофф, Дж. Х. (1874) «Sur les Formulas de Structure dans l'espace» (О структурных формулах в пространстве), Archives Néerlandaises des Sciences Exactes et Naturelles , 9 : 445–454.
- ^ Ле Бель, Ж.-А. (1874) «Sur les Relations qui Existent entre les Formulas Atomiques des Corps Organiques et le pouvoir rotatoire de leurs Dissolutions» (Об отношениях, которые существуют между атомными формулами органических веществ и вращательной силой их растворов), Bulletin de la Société Химик де Пари , 22 : 337–347.
- ^ Банн, CW (1945). Химическая кристаллография . Нью-Йорк: Oxford University Press. стр. 88.
- ^ Р. Уильямс (1968). "Оптический вращательный эффект в нематической жидкой фазе п-азоксианизола". Physical Review Letters . 21 (6): 342. Bibcode : 1968PhRvL..21..342W. doi : 10.1103/PhysRevLett.21.342.
- ^ Р. Уильямс (1969). "Оптически-вращательная сила и линейный электрооптический эффект в нематических жидких кристаллах п-азоксианизола". Журнал химической физики . 50 (3): 1324. Bibcode : 1969JChPh..50.1324W. doi : 10.1063/1.1671194.
- ^ Вавилов, С. И. (1950). Микроструктура света . М.: Изд-во АН СССР.
- ^ Ахманов, С.А.; Жданов Б.В.; Желудев Н.И.; Ковригин А.И.; Кузнецов, В.И. (1979). «Нелинейная оптическая активность в кристаллах». Письма ЖЭТФ . 29 : 264.
- ^ Сильверман, М.; Ритчи, Н.; Кушман, Г.; Фишер, Б. (1988). «Экспериментальные конфигурации, использующие оптическую фазовую модуляцию для измерения хиральных асимметрий в свете, зеркально отраженном от естественно гиротропной среды». Журнал оптического общества Америки A . 5 (11): 1852. Bibcode :1988JOSAA...5.1852S. doi :10.1364/JOSAA.5.001852.
- ^ Silverman, M.; Badoz, J.; Briat, B. (1992). "Хиральное отражение от естественно оптически активной среды". Optics Letters . 17 (12): 886. Bibcode : 1992OptL...17..886S. doi : 10.1364/OL.17.000886. PMID 19794663.
- ^ Бозе, Джагадис Чандер (1898). «О вращении плоскости поляризации электрических волн скрученной структурой». Труды Королевского общества . 63 (389–400): 146–152. doi :10.1098/rspl.1898.0019. JSTOR 115973. S2CID 89292757.
- ^ Свирко, Ю.; Желудев, НИ; Осипов, М. (2001). «Слоистые хиральные металлические микроструктуры с индуктивной связью». Applied Physics Letters . 78 (4): 498. Bibcode :2001ApPhL..78..498S. doi :10.1063/1.1342210.
- ^ Кувата-Гоноками, М.; Сайто, Н.; Ино, Ю.; Кауранен, М.; Ефимовы, К.; Валлиус, Т.; Турунен Дж.; Свирко, Ю. (2005). «Гигантская оптическая активность в квазидвумерных плоских наноструктурах». Письма о физических отзывах . 95 (22): 227401. Бибкод : 2005PhRvL..95v7401K. doi : 10.1103/PhysRevLett.95.227401. ПМИД 16384264.
- ^ Plum, E.; Fedotov, VA; Schwanecke, AS; Zheludev, NI; Chen, Y. (2007). "Гигантская оптическая гиротропия из-за электромагнитной связи". Applied Physics Letters . 90 (22): 223113. Bibcode : 2007ApPhL..90v3113P. doi : 10.1063/1.2745203.
- ^ Plum, E.; Fedotov, VA; Zheludev, NI (2008). "Оптическая активность во внешне хиральном метаматериале" (PDF) . Applied Physics Letters . 93 (19): 191911. arXiv : 0807.0523 . Bibcode :2008ApPhL..93s1911P. doi :10.1063/1.3021082. S2CID 117891131.
- ^ Plum, E.; Fedotov, VA; Zheludev, NI (2016). "Зеркальная оптическая активность ахиральных метаповерхностей" (PDF) . Applied Physics Letters . 108 (14): 141905. Bibcode :2016ApPhL.108n1905P. doi :10.1063/1.4944775. hdl :10220/40854.
- ^ Ren, M.; Plum, E.; Xu, J.; Zheludev, NI (2012). "Гигантская нелинейная оптическая активность в плазмонном метаматериале". Nature Communications . 3 : 833. Bibcode : 2012NatCo...3..833R. doi : 10.1038/ncomms1805 . PMID 22588295.
- ^ ab Л. Д. Ландау ; Е. М. Лифшиц ; Л. П. Питаевский (1984). Электродинамика сплошных сред . Т. 8 (2-е изд.). Баттерворт-Хайнеман . С. 362–365. ISBN 978-0-7506-2634-7.
- ^ Plum, E.; Zhou, J.; Dong, J.; Fedotov, VA; Koschny, T.; Soukoulis, CM; Zheludev, NI (2009). "Метаматериал с отрицательным индексом из-за хиральности" (PDF) . Physical Review B. 79 ( 3): 035407. Bibcode : 2009PhRvB..79c5407P. doi : 10.1103/PhysRevB.79.035407. S2CID 119259753.
- ^ Чжан, С.; Парк, И.-С.; Ли, Дж.; Лу, Х.; Чжан, В.; Чжан, Х. (2009). «Отрицательный показатель преломления в хиральных метаматериалах». Physical Review Letters . 102 (2): 023901. Bibcode : 2009PhRvL.102b3901Z. doi : 10.1103/PhysRevLett.102.023901. PMID 19257274.
Дальнейшее чтение
- Юджин Хехт, Оптика , 3-е изд., Addison-Wesley, 1998, ISBN 0-201-30425-2
- Ахлеш Лахтакия , Поля Бельтрами в хиральных средах, World Scientific, Сингапур, 1994 г.
- Пошаговое руководство по оптическому вращению
- Моррисон, Роберт Т., и Бойд, Роберт Н., Органическая химия (6-е изд.), Prentice-Hall Inc (1992).



























