10-кубовый

This article includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations. Please help improve this article by introducing more precise citations. (September 2022) (Learn how and when to remove this message)

10-кубовый Декеракт
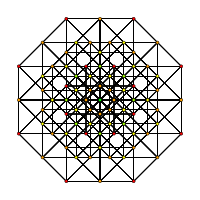
Ортогональная проекция внутри многоугольника Петри. Оранжевые вершины удвоены, а центральная желтая — имеет четыре.
Тип	Правильный 10-мерный многогранник e
Семья	гиперкуб
Символ Шлефли	{4,3 8 }
Диаграмма Коксетера-Дынкина
9-гранный	20 {4,3 7 }
8-гранный	180 {4,3 6 }
7-гранный	960 {4,3 5 }
6-гранный	3360 {4,3 4 }
5-гранный	8064 {4,3 3 }
4-х гранный	13440 {4,3,3}
Клетки	15360 {4,3}
Лица	11520 квадратов
Края	5120 сегментов
Вершины	1024 балла
Вершинная фигура	9-симплекс
Петри полигон	икосагон
Группа Коксетера	С 10 , [3 8 ,4]
Двойной	10-ортоплекс
Характеристики	выпуклый , многогранник Ганнера

В геометрии 10-куб — ​​это десятимерный гиперкуб . Он имеет 1024 вершины , 5120 ребер , 11520 квадратных граней , 15360 кубических ячеек , 13440 4-гранных тессерактов , 8064 5-гранных 5-куба , 3360 6-гранных 6-куба , 960 7-гранных 7-куба , 180 8-гранных 8-куба и 20 9-гранных 9-куба .

Его можно назвать по его символу Шлефли {4,3 ⁸ }, состоящему из 3 9-кубов вокруг каждой 8-грани. Иногда его называют декерактом , что является портманто тессеракта ( 4 - куб ) и дека- для десяти (измерений) по- гречески . Его также можно назвать икосаронноном или икоса-10-топом как 10-мерный многогранник , построенный из 20 правильных граней .

Он является частью бесконечного семейства многогранников , называемых гиперкубами . Двойственный к декеракту многогранник можно назвать 10-ортоплексом или декакросом, и он является частью бесконечного семейства кросс-политопов .

Декартовы координаты для вершин декарта с центром в начале координат и длиной ребра 2 равны

(±1,±1,±1,±1,±1,±1,±1,±1,±1,±1)

в то время как внутренняя часть состоит из всех точек ( x ₀ , x ₁ , x ₂ , x ₃ , x ₄ , x ₅ , x ₆ , x ₇ , x ₈ , x ₉ ) с −1 <  x _i  < 1.

Этот 10-кубовый граф является ортогональной проекцией . Эта ориентация показывает столбцы вершин, расположенных на расстоянии вершина-ребро-вершина от одной вершины слева до одной вершины справа, и ребра, соединяющие соседние столбцы вершин. Количество вершин в каждом столбце представляет строки в треугольнике Паскаля , будучи 1:10:45:120:210:252:210:120:45:10:1.

Ортографические проекции

Б 10	Б 9	Б 8
[20]	[18]	[16]
Б 7	Б 6	Б 5
[14]	[12]	[10]
Б 4	Б 3	Б 2
[8]	[6]	[4]
А 9		А 5
[10]		[6]
А 7		А 3
[8]		[4]

Применение операции чередования , удаляющей чередующиеся вершины декеракта , создает еще один однородный многогранник , называемый 10-демикубом (часть бесконечного семейства, называемого демигиперкубами ), который имеет 20 демиеннерактических и 512 эннеацетонических граней.

• HSM Коксетер :
  • Коксетер, Правильные многогранники , (3-е издание, 1973), издание Дувра, ISBN  0-486-61480-8 , стр.296, Таблица I (iii): Правильные многогранники, три правильных многогранника в n-мерности (n≥5)
  • HSM Coxeter, Regular Polytopes , 3-е издание, Dover New York, 1973, стр. 296, Таблица I (iii): Regular Polytopes, три regular polytopes в n-мерностях (n≥5)
  • Калейдоскопы: избранные труды Х. С. М. Коксетера , под редакцией Ф. Артура Шерка, Питера МакМаллена, Энтони К. Томпсона, Азии Айвик Вайс, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1] 
    • (Документ 22) HSM Coxeter, Правильные и полуправильные многогранники I , [Math. Zeit. 46 (1940) 380–407, MR 2,10]
    • (Документ 23) HSM Coxeter, Правильные и полуправильные многогранники II , [Math. Zeit. 188 (1985) 559-591]
    • (Документ 24) HSM Coxeter, Правильные и полуправильные многогранники III , [Math. Zeit. 200 (1988) 3-45]
• Норман Джонсон Однородные многогранники , Рукопись (1991)
  • Н. В. Джонсон: Теория однородных многогранников и сот , доктор философии (1966)
• Клитцинг, Ричард. «10D однородные многогранники (поликсенна) o3o3o3o3o3o3o3o3o3o4x - декер».

• Вайсштейн, Эрик В. «Гиперкуб». MathWorld .
• Ольшевский, Джордж. "Измерение многогранника". Глоссарий для гиперпространства . Архивировано из оригинала 4 февраля 2007 г.
• Многомерный глоссарий: гиперкуб Гарретт Джонс
• Последовательность OEIS A135289 (Гиперкубы:10-куб)