Гармонический осциллятор

Часть серии статей о
Классическая механика
${\displaystyle {\textbf {F}}={\frac {d\mathbf {p} }{dt}}}$ Second law of motion
History Timeline Textbooks
Branches Applied Celestial Continuum Dynamics Field theory Kinematics Kinetics Statics Statistical mechanics
Fundamentals Acceleration Angular momentum Couple D'Alembert's principle Energy kinetic potential Force Frame of reference Inertial frame of reference Impulse Inertia / Moment of inertia Mass Mechanical power Mechanical work Moment Momentum Space Speed Time Torque Velocity Virtual work
Formulations Newton's laws of motion Analytical mechanics Lagrangian mechanics Hamiltonian mechanics Routhian mechanics Hamilton–Jacobi equation Appell's equation of motion Koopman–von Neumann mechanics
Core topics Damping Displacement Equations of motion Euler's laws of motion Fictitious force Friction Harmonic oscillator Inertial / Non-inertial reference frame Motion (linear) Newton's law of universal gravitation Newton's laws of motion Relative velocity Rigid body dynamics Euler's equations Simple harmonic motion Vibration
Rotation Circular motion Rotating reference frame Centripetal force Centrifugal force reactive Coriolis force Pendulum Tangential speed Rotational frequency Angular acceleration / displacement / frequency / velocity
Scientists Kepler Galileo Huygens Newton Horrocks Halley Maupertuis Daniel Bernoulli Johann Bernoulli Euler d'Alembert Clairaut Lagrange Laplace Poisson Hamilton Jacobi Cauchy Routh Liouville Appell Gibbs Koopman von Neumann
Physics portal  Category
v t e

В классической механике гармонический осциллятор — это система, которая при смещении из положения равновесия испытывает восстанавливающую силу F, пропорциональную смещению x : F → = − k x → , {\displaystyle {\vec {F}}=-k{\vec {x}},} где k — положительная константа .

Если F — единственная сила, действующая на систему, то система называется простым гармоническим осциллятором и совершает простые гармонические колебания : синусоидальные колебания около точки равновесия с постоянной амплитудой и постоянной частотой (которая не зависит от амплитуды).

Если также присутствует сила трения ( затухание ), пропорциональная скорости , гармонический осциллятор описывается как затухающий осциллятор . В зависимости от коэффициента трения система может:

• Колеблются с частотой ниже, чем в случае незатухания , и амплитудой, уменьшающейся со временем ( незатухающий осциллятор).
• Возвращение в положение равновесия без колебаний ( перезатухающий осциллятор).

Граничное решение между недодемпфированным осциллятором и передемпфированным осциллятором возникает при определенном значении коэффициента трения и называется критически затухающим .

Если присутствует внешняя сила, зависящая от времени, гармонический осциллятор описывается как ведомый осциллятор .

Механические примеры включают маятники (с малыми углами смещения ), массы, соединенные с пружинами , и акустические системы . Другие аналогичные системы включают электрические гармонические осцилляторы, такие как RLC-цепи . Модель гармонического осциллятора очень важна в физике, потому что любая масса, подверженная силе в устойчивом равновесии, действует как гармонический осциллятор для малых колебаний. Гармонические осцилляторы широко распространены в природе и используются во многих искусственных устройствах, таких как часы и радиосхемы. Они являются источником практически всех синусоидальных колебаний и волн.

Простой гармонический осциллятор — это осциллятор, который не приводится в движение и не затухает . Он состоит из массы m , которая испытывает одну силу F , которая тянет массу в направлении точки x = 0 и зависит только от положения x массы и константы k . Баланс сил ( второй закон Ньютона ) для системы:$${\displaystyle F=ma=m{\frac {\mathrm {d} ^{2}x}{\mathrm {d} t^{2}}}=m{\ddot {x}}=-kx.}$$

Решая это дифференциальное уравнение , находим, что движение описывается функцией x ( t ) = A sin ⁡ ( ω t + φ ) , {\displaystyle x(t)=A\sin(\omega t+\varphi ),} где ω = k m . {\displaystyle \omega ={\sqrt {\frac {k}{m}}}.}

Движение является периодическим , повторяющимся по синусоидальному закону с постоянной амплитудой A. В дополнение к амплитуде, движение простого гармонического осциллятора характеризуется его периодом , временем одного колебания или его частотой , числом циклов в единицу времени. Положение в данный момент времени t также зависит от фазы φ , которая определяет начальную точку на синусоиде. Период и частота определяются размером массы m и силовой постоянной k , в то время как амплитуда и фаза определяются начальным положением и скоростью .${\displaystyle T=2\pi /\omega }$${\displaystyle f=1/T}$

Скорость и ускорение простого гармонического осциллятора колеблются с той же частотой, что и положение, но со сдвинутыми фазами. Скорость максимальна при нулевом смещении, а ускорение направлено в сторону, противоположную смещению.

Потенциальная энергия, запасенная в простом гармоническом осцилляторе в точке x, равна U = 1 2 k x 2 . {\displaystyle U={\tfrac {1}{2}}kx^{2}.}

В реальных осцилляторах трение или затухание замедляет движение системы. Из-за силы трения скорость уменьшается пропорционально действующей силе трения. В то время как в простом невозбужденном гармоническом осцилляторе единственной силой, действующей на массу, является восстанавливающая сила, в затухающем гармоническом осцилляторе есть еще сила трения, которая всегда направлена ​​в сторону, противоположную движению. Во многих вибрирующих системах сила трения F _f может быть смоделирована как пропорциональная скорости v объекта: F _f = − cv , где c называется коэффициентом вязкого затухания .

Тогда баланс сил ( второй закон Ньютона ) для затухающих гармонических осцилляторов равен ^{[1] [2] [3]} , что можно переписать в виде , где$${\displaystyle F=-kx-c{\frac {\mathrm {d} x}{\mathrm {d} t}}=m{\frac {\mathrm {d} ^{2}x}{\mathrm {d} t^{2}}},}$$$${\displaystyle {\frac {\mathrm {d} ^{2}x}{\mathrm {d} t^{2}}}+2\zeta \omega _{0}{\frac {\mathrm {d} x}{\mathrm {d} t}}+\omega _{0}^{2}x=0,}$$

• ${\textstyle \omega _{0}={\sqrt {\frac {k}{m}}}}$называется «незатухающей угловой частотой осциллятора»,
• ζ = c 2 m k {\textstyle \zeta ={\frac {c}{2{\sqrt {mk}}}}} называется «коэффициентом затухания».

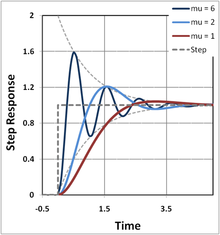
Значение коэффициента затухания ζ критически определяет поведение системы. Затухающий гармонический осциллятор может быть:

• Сверхдемпфированный ( ζ > 1): Система возвращается ( экспоненциально затухает ) в устойчивое состояние без колебаний. Большие значения коэффициента затухания ζ возвращают к равновесию медленнее.
• Критически затухающий ( ζ = 1): Система возвращается в устойчивое состояние как можно быстрее без колебаний (хотя может произойти перерегулирование, если начальная скорость не равна нулю). Это часто желательно для затухания таких систем, как двери.
• Незатухающий ( ζ < 1): Система колеблется (с немного другой частотой, чем в случае незатухающего) с амплитудой, постепенно уменьшающейся до нуля. Угловая частота затухающего гармонического осциллятора определяется экспоненциальным затуханием затухающего гармонического осциллятора, которое определяется как${\textstyle \omega _{1}=\omega _{0}{\sqrt {1-\zeta ^{2}}},}$${\displaystyle \lambda =\omega _{0}\zeta .}$

Добротность затухающего осциллятора определяется как $${\displaystyle Q=2\pi \times {\frac {\text{energy stored}}{\text{energy lost per cycle}}}.}$$

Q связано с коэффициентом затухания соотношением${\textstyle Q={\frac {1}{2\zeta }}.}$

Возбужденные гармонические осцилляторы представляют собой затухающие осцилляторы, на которые дополнительно воздействует внешняя приложенная сила F ( t ).

Второй закон Ньютона принимает форму$${\displaystyle F(t)-kx-c{\frac {\mathrm {d} x}{\mathrm {d} t}}=m{\frac {\mathrm {d} ^{2}x}{\mathrm {d} t^{2}}}.}$$

Обычно его переписывают в форму$${\displaystyle {\frac {\mathrm {d} ^{2}x}{\mathrm {d} t^{2}}}+2\zeta \omega _{0}{\frac {\mathrm {d} x}{\mathrm {d} t}}+\omega _{0}^{2}x={\frac {F(t)}{m}}.}$$

Это уравнение можно решить точно для любой движущей силы, используя решения z ( t ), которые удовлетворяют невынужденному уравнению$${\displaystyle {\frac {\mathrm {d} ^{2}z}{\mathrm {d} t^{2}}}+2\zeta \omega _{0}{\frac {\mathrm {d} z}{\mathrm {d} t}}+\omega _{0}^{2}z=0,}$$

и которые можно выразить как затухающие синусоидальные колебания: в случае, когда ζ ≤ 1. Амплитуда A и фаза φ определяют поведение, необходимое для соответствия начальным условиям.$${\displaystyle z(t)=Ae^{-\zeta \omega _{0}t}\sin \left({\sqrt {1-\zeta ^{2}}}\omega _{0}t+\varphi \right),}$$

В случае ζ < 1 и единичного шага входного сигнала с  x (0) = 0 : решение имеет вид$${\displaystyle {\frac {F(t)}{m}}={\begin{cases}\omega _{0}^{2}&t\geq 0\\0&t<0\end{cases}}}$$$${\displaystyle x(t)=1-e^{-\zeta \omega _{0}t}{\frac {\sin \left({\sqrt {1-\zeta ^{2}}}\omega _{0}t+\varphi \right)}{\sin(\varphi )}},}$$

с фазой φ, заданной формулой

$${\displaystyle \cos \varphi =\zeta .}$$

Время, необходимое осциллятору для адаптации к изменившимся внешним условиям, имеет порядок τ = 1/( ζω ₀ ) . В физике адаптация называется релаксацией , а τ — временем релаксации.

В электротехнике кратное τ называется временем установления , т. е. временем, необходимым для того, чтобы сигнал находился в пределах фиксированного отклонения от конечного значения, обычно в пределах 10%. Термин « перерегулирование» относится к степени, в которой максимум отклика превышает конечное значение, а «недорегулирование» относится к степени, в которой отклик падает ниже конечного значения для времени, следующего за максимумом отклика.

В случае синусоидальной движущей силы: где - амплитуда движения, а - частота движения для синусоидального приводного механизма. Этот тип системы появляется в управляемых переменным током RLC-цепях ( резистор - индуктор - конденсатор ) и управляемых пружинных системах, имеющих внутреннее механическое сопротивление или внешнее сопротивление воздуха .$${\displaystyle {\frac {\mathrm {d} ^{2}x}{\mathrm {d} t^{2}}}+2\zeta \omega _{0}{\frac {\mathrm {d} x}{\mathrm {d} t}}+\omega _{0}^{2}x={\frac {1}{m}}F_{0}\sin(\omega t),}$$${\displaystyle F_{0}}$${\displaystyle \omega }$

Общее решение представляет собой сумму переходного решения, зависящего от начальных условий, и установившегося состояния , которое не зависит от начальных условий и зависит только от амплитуды возбуждения , частоты возбуждения , незатухающей угловой частоты и коэффициента затухания .${\displaystyle F_{0}}$${\displaystyle \omega }$${\displaystyle \omega _{0}}$${\displaystyle \zeta }$

Стационарное решение пропорционально движущей силе с индуцированным изменением фазы : где Z m = ( 2 ω 0 ζ ) 2 + 1 ω 2 ( ω 0 2 − ω 2 ) 2 {\displaystyle Z_{m}={\sqrt {\left(2\omega _{0}\zeta \right)^{2}+{\frac {1}{\omega ^{2}}}(\omega _{0}^{2}-\omega ^{2})^{2}}}} — абсолютное значение импеданса или линейной функции отклика , а${\displaystyle \varphi }$$${\displaystyle x(t)={\frac {F_{0}}{mZ_{m}\omega }}\sin(\omega t+\varphi ),}$$$${\displaystyle \varphi =\arctan \left({\frac {2\omega \omega _{0}\zeta }{\omega ^{2}-\omega _{0}^{2}}}\right)+n\pi }$$

— фаза колебания относительно движущей силы. Значение фазы обычно принимается между −180° и 0 (то есть оно представляет собой фазовую задержку, как для положительных, так и для отрицательных значений аргумента arctan).

Для определенной частоты возбуждения, называемой резонансом , или резонансной частотой , амплитуда (для заданного ) максимальна. Этот резонансный эффект возникает только при , т.е. для значительно недодемпфированных систем. Для сильно недодемпфированных систем значение амплитуды может стать довольно большим вблизи резонансной частоты.${\textstyle \omega _{r}=\omega _{0}{\sqrt {1-2\zeta ^{2}}}}$${\displaystyle F_{0}}$${\displaystyle \zeta <1/{\sqrt {2}}}$

Переходные решения такие же, как и невынужденный ( ) затухающий гармонический осциллятор, и представляют собой реакцию системы на другие события, которые произошли ранее. Переходные решения обычно затухают достаточно быстро, чтобы их можно было игнорировать.${\displaystyle F_{0}=0}$

Параметрический осциллятор — это управляемый гармонический осциллятор, в котором энергия привода обеспечивается изменением параметров осциллятора, таких как демпфирующая или восстанавливающая сила. Известным примером параметрических колебаний является «накачка» на качелях на детской площадке . ^{[4] [5] [6]} Человек на движущихся качелях может увеличить амплитуду колебаний качелей без применения какой-либо внешней движущей силы (толчков), изменяя момент инерции качелей, раскачиваясь вперед и назад («накачка») или попеременно стоя и приседая в ритме с колебаниями качелей. Изменение параметров приводит в движение систему. Примерами параметров, которые могут изменяться, являются ее резонансная частота и затухание .${\displaystyle \omega }$${\displaystyle \beta }$

Параметрические генераторы используются во многих приложениях. Классический параметрический генератор варакторов колеблется, когда емкость диода периодически изменяется. Схема, которая изменяет емкость диода, называется «насосом» или «драйвером». В микроволновой электронике параметрические генераторы на основе волновода / YAG работают таким же образом. Разработчик периодически изменяет параметр, чтобы вызвать колебания.

Параметрические генераторы были разработаны как малошумящие усилители, особенно в диапазоне радиочастот и микроволновых волн. Тепловой шум минимален, поскольку изменяется реактивное сопротивление (а не сопротивление). Другое распространенное применение — преобразование частоты, например, преобразование из аудио в радиочастоты. Например, оптический параметрический генератор преобразует входную лазерную волну в две выходные волны более низкой частоты ( ).${\displaystyle \omega _{s},\omega _{i}}$

Параметрический резонанс возникает в механической системе, когда система параметрически возбуждается и колеблется на одной из своих резонансных частот. Параметрическое возбуждение отличается от принуждения, поскольку действие проявляется как изменяющееся во времени изменение параметра системы. Этот эффект отличается от обычного резонанса, поскольку он демонстрирует явление неустойчивости .

Уравнение известно как уравнение универсального осциллятора , поскольку все линейные колебательные системы второго порядка можно привести к этой форме. ^{[ необходима ссылка ]} Это делается посредством обезразмеривания .$${\displaystyle {\frac {\mathrm {d} ^{2}q}{\mathrm {d} \tau ^{2}}}+2\zeta {\frac {\mathrm {d} q}{\mathrm {d} \tau }}+q=0}$$

Если функция принуждения равна f ( t ) = cos( ωt ) = cos( ωt _c τ ) = cos( ωτ ) , где ω = ωt _c , уравнение принимает вид$${\displaystyle {\frac {\mathrm {d} ^{2}q}{\mathrm {d} \tau ^{2}}}+2\zeta {\frac {\mathrm {d} q}{\mathrm {d} \tau }}+q=\cos(\omega \tau ).}$$

Решение этого дифференциального уравнения содержит две части: «переходную» и «установившуюся».

Решение, основанное на решении обыкновенного дифференциального уравнения , для произвольных констант c ₁ и c ₂

$${\displaystyle q_{t}(\tau )={\begin{cases}e^{-\zeta \tau }\left(c_{1}e^{\tau {\sqrt {\zeta ^{2}-1}}}+c_{2}e^{-\tau {\sqrt {\zeta ^{2}-1}}}\right)&\zeta >1{\text{ (overdamping)}}\\e^{-\zeta \tau }(c_{1}+c_{2}\tau )=e^{-\tau }(c_{1}+c_{2}\tau )&\zeta =1{\text{ (critical damping)}}\\e^{-\zeta \tau }\left[c_{1}\cos \left({\sqrt {1-\zeta ^{2}}}\tau \right)+c_{2}\sin \left({\sqrt {1-\zeta ^{2}}}\tau \right)\right]&\zeta <1{\text{ (underdamping)}}\end{cases}}}$$

Переходное решение не зависит от вынуждающей функции.

Примените « метод комплексных переменных », решив вспомогательное уравнение ниже, а затем найдя действительную часть его решения:$${\displaystyle {\frac {\mathrm {d} ^{2}q}{\mathrm {d} \tau ^{2}}}+2\zeta {\frac {\mathrm {d} q}{\mathrm {d} \tau }}+q=\cos(\omega \tau )+i\sin(\omega \tau )=e^{i\omega \tau }.}$$

Предположим, что решение имеет вид$${\displaystyle q_{s}(\tau )=Ae^{i(\omega \tau +\varphi )}.}$$

Его производные от нулевого до второго порядка равны$${\displaystyle q_{s}=Ae^{i(\omega \tau +\varphi )},\quad {\frac {\mathrm {d} q_{s}}{\mathrm {d} \tau }}=i\omega Ae^{i(\omega \tau +\varphi )},\quad {\frac {\mathrm {d} ^{2}q_{s}}{\mathrm {d} \tau ^{2}}}=-\omega ^{2}Ae^{i(\omega \tau +\varphi )}.}$$

Подстановка этих величин в дифференциальное уравнение дает$${\displaystyle -\omega ^{2}Ae^{i(\omega \tau +\varphi )}+2\zeta i\omega Ae^{i(\omega \tau +\varphi )}+Ae^{i(\omega \tau +\varphi )}=(-\omega ^{2}A+2\zeta i\omega A+A)e^{i(\omega \tau +\varphi )}=e^{i\omega \tau }.}$$

Деление на экспоненциальный член слева дает$${\displaystyle -\omega ^{2}A+2\zeta i\omega A+A=e^{-i\varphi }=\cos \varphi -i\sin \varphi .}$$

Приравнивая действительную и мнимую части, получаем два независимых уравнения$${\displaystyle A(1-\omega ^{2})=\cos \varphi ,\quad 2\zeta \omega A=-\sin \varphi .}$$

Возводя оба уравнения в квадрат и складывая их, получаем$${\displaystyle \left.{\begin{aligned}A^{2}(1-\omega ^{2})^{2}&=\cos ^{2}\varphi \\(2\zeta \omega A)^{2}&=\sin ^{2}\varphi \end{aligned}}\right\}\Rightarrow A^{2}[(1-\omega ^{2})^{2}+(2\zeta \omega )^{2}]=1.}$$

Поэтому,$${\displaystyle A=A(\zeta ,\omega )=\operatorname {sgn} \left({\frac {-\sin \varphi }{2\zeta \omega }}\right){\frac {1}{\sqrt {(1-\omega ^{2})^{2}+(2\zeta \omega )^{2}}}}.}$$

Сравните этот результат с разделом теории о резонансе , а также с «частью амплитуды» цепи RLC . Эта амплитудная функция особенно важна при анализе и понимании частотной характеристики систем второго порядка.

Чтобы решить для φ , разделите оба уравнения, чтобы получить$${\displaystyle \tan \varphi =-{\frac {2\zeta \omega }{1-\omega ^{2}}}={\frac {2\zeta \omega }{\omega ^{2}-1}}~~\implies ~~\varphi \equiv \varphi (\zeta ,\omega )=\arctan \left({\frac {2\zeta \omega }{\omega ^{2}-1}}\right)+n\pi .}$$

Эта фазовая функция особенно важна для анализа и понимания частотной характеристики систем второго порядка.

Объединение амплитудной и фазовой частей приводит к стационарному решению$${\displaystyle q_{s}(\tau )=A(\zeta ,\omega )\cos(\omega \tau +\varphi (\zeta ,\omega ))=A\cos(\omega \tau +\varphi ).}$$

Решение исходного уравнения универсального осциллятора представляет собой суперпозицию (сумму) переходного и стационарного решений:$${\displaystyle q(\tau )=q_{t}(\tau )+q_{s}(\tau ).}$$

Гармонические осцилляторы, встречающиеся в ряде областей техники, эквивалентны в том смысле, что их математические модели идентичны (см. уравнение универсального осциллятора выше). Ниже приведена таблица, показывающая аналогичные величины в четырех системах гармонических осцилляторов в механике и электронике. Если аналогичным параметрам в одной строке таблицы приданы численно равные значения, поведение осцилляторов — их выходная форма волны, резонансная частота, коэффициент затухания и т. д. — будет одинаковым.

Трансляционно-механический	Вращательный механический	Последовательная цепь RLC	Параллельная RLC-цепь
Позиция${\displaystyle x}$	Угол${\displaystyle \theta }$	Заряжать ${\displaystyle q}$	Потокосцепление ${\displaystyle \varphi }$
Скорость ${\displaystyle {\frac {\mathrm {d} x}{\mathrm {d} t}}}$	Угловая скорость ${\displaystyle {\frac {\mathrm {d} \theta }{\mathrm {d} t}}}$	Текущий ${\displaystyle {\frac {\mathrm {d} q}{\mathrm {d} t}}}$	Напряжение ${\displaystyle {\frac {\mathrm {d} \varphi }{\mathrm {d} t}}}$
Масса ${\displaystyle m}$	Момент инерции ${\displaystyle I}$	Индуктивность ${\displaystyle L}$	Емкость ${\displaystyle C}$
Импульс ${\displaystyle p}$	Угловой момент импульса ${\displaystyle L}$	Потокосцепление ${\displaystyle \varphi }$	Заряжать ${\displaystyle q}$
Жесткость пружины ${\displaystyle k}$	Постоянная кручения ${\displaystyle \mu }$	Эластичность ${\displaystyle 1/C}$	Магнитное сопротивление ${\displaystyle 1/L}$
Демпфирование ${\displaystyle c}$	Вращательное трение ${\displaystyle \Gamma }$	Сопротивление ${\displaystyle R}$	Проводимость ${\displaystyle G=1/R}$
Движущая сила ${\displaystyle F(t)}$	Крутящий момент привода ${\displaystyle \tau (t)}$	Напряжение ${\displaystyle v}$	Текущий ${\displaystyle i}$
Незатухающая резонансная частота :${\displaystyle f_{n}}$
${\displaystyle {\frac {1}{2\pi }}{\sqrt {\frac {k}{m}}}}$	${\displaystyle {\frac {1}{2\pi }}{\sqrt {\frac {\mu }{I}}}}$	${\displaystyle {\frac {1}{2\pi }}{\sqrt {\frac {1}{LC}}}}$	${\displaystyle {\frac {1}{2\pi }}{\sqrt {\frac {1}{LC}}}}$
Коэффициент затухания :${\displaystyle \zeta }$
${\displaystyle {\frac {c}{2}}{\sqrt {\frac {1}{km}}}}$	${\displaystyle {\frac {\Gamma }{2}}{\sqrt {\frac {1}{I\mu }}}}$	${\displaystyle {\frac {R}{2}}{\sqrt {\frac {C}{L}}}}$	${\displaystyle {\frac {G}{2}}{\sqrt {\frac {L}{C}}}}$
Дифференциальное уравнение:
${\displaystyle m{\ddot {x}}+c{\dot {x}}+kx=F}$	${\displaystyle I{\ddot {\theta }}+\Gamma {\dot {\theta }}+\mu \theta =\tau }$	${\displaystyle L{\ddot {q}}+R{\dot {q}}+q/C=v}$	${\displaystyle C{\ddot {\varphi }}+G{\dot {\varphi }}+\varphi /L=i}$

Проблема простого гармонического осциллятора часто возникает в физике, поскольку масса, находящаяся в равновесии под действием любой консервативной силы , в пределе малых движений ведет себя как простой гармонический осциллятор.

Консервативная сила — это сила, связанная с потенциальной энергией . Функция потенциальной энергии гармонического осциллятора имеет вид$${\displaystyle V(x)={\tfrac {1}{2}}kx^{2}.}$$

При наличии произвольной функции потенциальной энергии можно выполнить разложение Тейлора относительно минимума энергии ( ), чтобы смоделировать поведение малых возмущений от равновесия.${\displaystyle V(x)}$${\displaystyle x}$${\displaystyle x=x_{0}}$

$${\displaystyle V(x)=V(x_{0})+V'(x_{0})\cdot (x-x_{0})+{\tfrac {1}{2}}V''(x_{0})\cdot (x-x_{0})^{2}+O(x-x_{0})^{3}.}$$

Поскольку является минимумом, первая производная, вычисленная при , должна быть равна нулю, поэтому линейный член отпадает:${\displaystyle V(x_{0})}$${\displaystyle x_{0}}$$${\displaystyle V(x)=V(x_{0})+{\tfrac {1}{2}}V''(x_{0})\cdot (x-x_{0})^{2}+O(x-x_{0})^{3}.}$$

Постоянный член V ( x ₀ ) является произвольным и, таким образом, может быть опущен, а преобразование координат позволяет восстановить форму простого гармонического осциллятора:$${\displaystyle V(x)\approx {\tfrac {1}{2}}V''(0)\cdot x^{2}={\tfrac {1}{2}}kx^{2}.}$$

Таким образом, имея произвольную функцию потенциальной энергии с ненулевой второй производной, можно использовать решение простого гармонического осциллятора, чтобы получить приближенное решение для малых возмущений вокруг точки равновесия.${\displaystyle V(x)}$

Предполагая отсутствие затухания, дифференциальное уравнение, управляющее простым маятником длиной , где — локальное ускорение силы тяжести , имеет вид d 2 θ d t 2 + g l sin ⁡ θ = 0. {\displaystyle {\frac {d^{2}\theta }{dt^{2}}}+{\frac {g}{l}}\sin \theta =0.} ${\displaystyle l}$${\displaystyle g}$

Если максимальное смещение маятника мало, мы можем воспользоваться приближением и вместо этого рассмотреть уравнение${\displaystyle \sin \theta \approx \theta }$$${\displaystyle {\frac {d^{2}\theta }{dt^{2}}}+{\frac {g}{l}}\theta =0.}$$

Общее решение этого дифференциального уравнения имеет вид , где и — константы, зависящие от начальных условий. Используя в качестве начальных условий и , решение задается выражением , где — наибольший угол, достигаемый маятником (то есть — амплитуда маятника). Период , время одного полного колебания, задается выражением τ = 2 π l g = 2 π ω , {\displaystyle \tau =2\pi {\sqrt {\frac {l}{g}}}={\frac {2\pi }{\omega }},} что является хорошим приближением фактического периода, когда мало. Обратите внимание, что в этом приближении период не зависит от амплитуды . В приведенном выше уравнении представляет угловую частоту.$${\displaystyle \theta (t)=A\cos \left({\sqrt {\frac {g}{l}}}t+\varphi \right),}$$${\displaystyle A}$${\displaystyle \varphi }$${\displaystyle \theta (0)=\theta _{0}}$${\displaystyle {\dot {\theta }}(0)=0}$$${\displaystyle \theta (t)=\theta _{0}\cos \left({\sqrt {\frac {g}{l}}}t\right),}$$${\displaystyle \theta _{0}}$${\displaystyle \theta _{0}}$${\displaystyle \theta _{0}}$${\displaystyle \tau }$${\displaystyle \theta _{0}}$${\displaystyle \omega }$

Когда пружина растягивается или сжимается массой, пружина развивает восстанавливающую силу. Закон Гука дает соотношение силы, оказываемой пружиной, когда пружина сжимается или растягивается на определенную длину: где F — сила, k — константа пружины, а x — смещение массы относительно положения равновесия. Знак минус в уравнении указывает на то, что сила, оказываемая пружиной, всегда действует в направлении, противоположном смещению (т. е. сила всегда действует по направлению к нулевому положению), и таким образом не дает массе улететь в бесконечность.$${\displaystyle F(t)=-kx(t),}$$

Используя метод баланса сил или энергии, можно легко показать, что движение этой системы задается следующим дифференциальным уравнением: последнее представляет собой второй закон движения Ньютона .$${\displaystyle F(t)=-kx(t)=m{\frac {\mathrm {d} ^{2}}{\mathrm {d} t^{2}}}x(t)=ma,}$$

Если начальное смещение равно A и начальная скорость отсутствует, решение этого уравнения имеет вид$${\displaystyle x(t)=A\cos \left({\sqrt {\frac {k}{m}}}t\right).}$$

При наличии идеальной безмассовой пружины, это масса на конце пружины. Если сама пружина имеет массу, ее эффективная масса должна быть включена в .${\displaystyle m}$${\displaystyle m}$

С точки зрения энергии, все системы имеют два типа энергии: потенциальную энергию и кинетическую энергию . Когда пружина растягивается или сжимается, она сохраняет упругую потенциальную энергию, которая затем преобразуется в кинетическую энергию. Потенциальная энергия внутри пружины определяется уравнением${\textstyle U={\frac {1}{2}}kx^{2}.}$

Когда пружина растягивается или сжимается, кинетическая энергия массы преобразуется в потенциальную энергию пружины. По закону сохранения энергии, предполагая, что точка отсчета определена в положении равновесия, когда пружина достигает своей максимальной потенциальной энергии, кинетическая энергия массы равна нулю. Когда пружина отпускается, она пытается вернуться в состояние равновесия, и вся ее потенциальная энергия преобразуется в кинетическую энергию массы.

Символ	Определение	Размеры	Единицы СИ
${\displaystyle a}$	Ускорение массы	${\displaystyle {\mathsf {LT^{-2}}}}$	м/с 2
${\displaystyle A}$	Пиковая амплитуда колебаний	${\displaystyle {\mathsf {L}}}$	м
${\displaystyle c}$	Коэффициент вязкого демпфирования	${\displaystyle {\mathsf {MT^{-1}}}}$	Н·с/м
${\displaystyle f}$	Частота	${\displaystyle {\mathsf {T^{-1}}}}$	Гц
${\displaystyle F}$	Движущая сила	${\displaystyle {\mathsf {MLT^{-2}}}}$	Н
${\displaystyle g}$	Ускорение силы тяжести на поверхности Земли	${\displaystyle {\mathsf {LT^{-2}}}}$	м/с 2
${\displaystyle i}$	Мнимая единица,${\displaystyle i^{2}=-1}$	—	—
${\displaystyle k}$	Жесткость пружины	${\displaystyle {\mathsf {MT^{-2}}}}$	Н/м
${\displaystyle \mu }$	Постоянная крутящего момента пружины	${\displaystyle {\mathsf {ML^{2}T^{-2}}}}$	Нм/рад
${\displaystyle m,M}$	Масса	${\displaystyle {\mathsf {M}}}$	кг
${\displaystyle Q}$	Фактор качества	—	—
${\displaystyle T}$	Период колебания	${\displaystyle {\mathsf {T}}}$	с
${\displaystyle t}$	Время	${\displaystyle {\mathsf {T}}}$	с
${\displaystyle U}$	Потенциальная энергия, запасенная в осцилляторе	${\displaystyle {\mathsf {ML^{2}T^{-2}}}}$	Дж.
${\displaystyle x}$	Положение массы	${\displaystyle {\mathsf {L}}}$	м
${\displaystyle \zeta }$	Коэффициент затухания	—	—
${\displaystyle \varphi }$	Фазовый сдвиг	—	рад
${\displaystyle \omega }$	Угловая частота	${\displaystyle {\mathsf {T^{-1}}}}$	рад/с
${\displaystyle \omega _{0}}$	Естественная резонансная угловая частота	${\displaystyle {\mathsf {T^{-1}}}}$	рад/с

• Фаулз, Грант Р.; Кэссидей, Джордж Л. (1986), Аналитическая механика (5-е изд.), Форт-Уэрт: Saunders College Publishing , ISBN 0-03-089725-4, LCCN  93085193
• Hayek, Sabih I. (15 апреля 2003 г.). "Механические колебания и демпфирование". Энциклопедия прикладной физики . WILEY-VCH Verlag GmbH & Co KGaA. doi :10.1002/3527600434.eap231. ISBN 9783527600434.
• Крейциг, Эрвин (1972), Высшая инженерная математика (3-е изд.), Нью-Йорк: Wiley , ISBN 0-471-50728-8
• Serway, Raymond A.; Jewett, John W. (2003). Физика для ученых и инженеров. Brooks/Cole. ISBN 0-534-40842-7.
• Типлер, Пол (1998). Физика для ученых и инженеров: Том 1 (4-е изд.). WH Freeman. ISBN 1-57259-492-6.
• Wylie, CR (1975). Advanced Engineering Mathematics (4-е изд.). McGraw-Hill. ISBN 0-07-072180-7.

На Викискладе есть медиафайлы по теме Гармонические осцилляторы .

В Викицитатнике есть цитаты, связанные с гармоническим осциллятором .

• Гармонический осциллятор из Фейнмановских лекций по физике