Бруннианская ссылка

В теории узлов , ветви топологии , брунновское зацепление — это нетривиальное зацепление , которое становится набором тривиальных несвязанных окружностей, если удалить любой компонент. Другими словами, разрезание любой петли освобождает все остальные петли (так что никакие две петли не могут быть напрямую связаны ).

Название Брунниан происходит в честь Германа Брунна . Статья Брунна « Über Verkettung» 1892 года включала примеры таких ссылок.

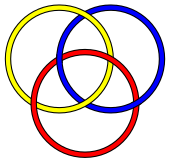
Наиболее известным и простым возможным зацеплением Брунна является кольцо Борромео , зацепление из трех узлов . Однако для каждого числа три или выше существует бесконечное число зацеплений с свойством Брунна, содержащих это число петель. Вот несколько относительно простых трехкомпонентных зацеплений Брунна, которые не являются тем же самым, что и кольца Борромео:

• 
  12-переходное звено.
• 
  18-переходное звено.
• 
  24-переходная ссылка.

Простейшим зацеплением Брунна, помимо 6-пересекающихся колец Борромео, предположительно является 10-пересекающееся зацепление L10a140 . ^[1]

Примером n- компонентной связи Брунна являются связи Брунна типа «резиновая лента», где каждый компонент закольцовывается вокруг следующего как aba ⁻¹ b ⁻¹ , причем последний закольцовывается вокруг первого, образуя круг. ^[2]

^{В 2020 году в [3]} были обнаружены новые и гораздо более сложные связи Брунна с использованием очень гибких методов геометрической топологии. См. раздел 6. ^[3]

Невозможно построить зацепление Брунна из геометрических окружностей. В более общем смысле, если зацепление обладает свойством, что каждый компонент является окружностью, и никакие два компонента не связаны, то оно тривиально. Доказательство Майкла Фридмана и Ричарда Скоры встраивает трехмерное пространство, содержащее зацепление, как границу модели шара Пуанкаре четырехмерного гиперболического пространства и рассматривает гиперболические выпуклые оболочки окружностей. Это двумерные подпространства гиперболического пространства, и их паттерны пересечения отражают попарное связывание окружностей: если две окружности связаны, то их оболочки имеют точку пересечения, но при условии, что пары окружностей не связаны, оболочки не пересекаются. Если взять сечения шара Пуанкаре концентрическими трехмерными сферами, то пересечение каждой сферы с оболочками окружностей снова будет связью, состоящей из окружностей, и это семейство сечений обеспечивает непрерывное движение всех окружностей, которое сжимает каждую из них в точку, не пересекая ни одну из других. ^[4]

Брунновские зацепления были классифицированы с точностью до гомотопии зацеплений Джоном Милнором в (Milnor 1954), а введенные им инварианты теперь называются инвариантами Милнора.

( n  + 1)-компонентное брунновское зацепление можно рассматривать как элемент группы зацеплений – которая в этом случае (но не в общем случае) является фундаментальной группой дополнения зацепления – n - компонентного несвязанного зацепления, поскольку по брунновости удаление последнего зацепления расцепляет остальные. Группа зацеплений n -компонентного несвязанного зацепления является свободной группой на n образующих, F _n , поскольку группа зацеплений одного зацепления является группой узлов неразвязанного зацепления , которая является целыми числами, а группа зацеплений несвязанного объединения является свободным произведением групп зацеплений компонентов.

Не каждый элемент группы связей даёт связь Брунна, поскольку удаление любого другого компонента должно также разорвать связь оставшихся n элементов. Милнор показал, что элементы группы, которые соответствуют связям Брунна, связаны с градуированной алгеброй Ли нижнего центрального ряда свободной группы, что можно интерпретировать как «отношения» в свободной алгебре Ли .

В 2021 году были исследованы две специальные операции сателлита для брунновских связей в 3-сфере, называемые «спутниковая сумма» и «спутниковая связь», обе из которых могут быть использованы для построения бесконечного числа различных брунновских связей из почти каждой брунновской связи. ^[5] Была дана теорема геометрической классификации для брунновских связей. ^[5] Что еще интереснее, было разработано каноническое геометрическое разложение в терминах спутниковой суммы и спутниковой связи, которое проще, чем JSJ-разложение, для брунновских связей. Строительными блоками брунновских связей в нем оказываются связи Хопфа, гиперболические брунновские связи и гиперболические брунновские связи в не связанных дополнениях, последняя из которых может быть дополнительно сведена к брунновской связи в 3-сфере. ^[5]

Брунновские связи можно понять в алгебраической топологии через произведения Масси : произведение Масси является n -кратным произведением, которое определено только в том случае, если все ( n  − 1)-кратные произведения его членов равны нулю. Это соответствует брунновскому свойству всех ( n  − 1)-компонентных подсвязей, которые не связаны, но общая n -компонентная связь нетривиально связана.

Брунновская коса — это коса, которая становится тривиальной при удалении любой из ее нитей. Брунновские косы образуют подгруппу группы кос . Брунновские косы над 2- сферой , которые не являются брунновскими над 2- диском, приводят к нетривиальным элементам в гомотопических группах 2-сферы. Например, «стандартная» коса, соответствующая кольцам Борромео, приводит к расслоению Хопфа S ³  →  S ² , и итерация этого (как в повседневном плетении) также является брунновской.

Многие головоломки на распутывание и некоторые механические головоломки являются вариантами брунновских связей, цель которых — освободить одну часть, лишь частично связанную с остальными, тем самым разобрав структуру.

Цепи Брунни также используются для создания предметов одежды и декора из эластичных лент с помощью таких устройств, как Rainbow Loom или Wonder Loom .

• Беррик, А. Джон; Коэн, Фредерик Р.; Вонг, Ян Лой; У, Цзе (2006), «Конфигурации, косы и гомотопические группы», Журнал Американского математического общества , 19 (2): 265– 326, doi : 10.1090/S0894-0347-05-00507-2 , MR  2188127.
• Герман Брунн, «Über Verkettung», Й. Мюнх. Бер, XXII. 77–99 (1892). JFM  24.0507.01 (на немецком языке)
• Милнор, Джон (март 1954 г.), «Группы связей», Annals of Mathematics , 59 (2), Annals of Mathematics: 177– 195, doi : 10.2307/1969685, JSTOR  1969685
• Рольфсен, Дейл (1976), Узлы и связи, серия лекций по математике, т. 7, Беркли, Калифорния : Publish or Perish, ISBN 0-914098-16-0, МР  0515288

На Викискладе есть медиафайлы по теме «Бруннианские ссылки» .

• «Так ли редки связи Борромео?», Славик Яблан (также доступно в оригинальной форме, опубликованной в журнале Forma здесь (файл PDF) Архивировано 28.02.2021 на Wayback Machine ).
• «Brunnian_link», Атлас узлов .