ссылка L10a140
Связка из трех петель с десятью перекрестками
Л10а140
Длина косы10
Номер косы3
Пересечение №10
Гиперболический объем12.27627758
нотация Конвея[.3:30]
ТистлтуэйтЛ10а140
Другой
чередование


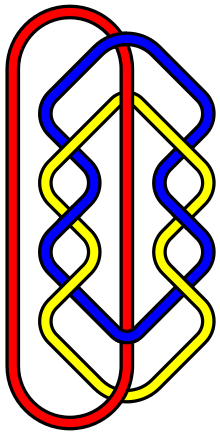
В математической теории узлов L10a140 — это название в таблице связей Тистлтуэйта связи из трех петель, которая имеет десять пересечений между петлями, если представлена ​​в ее простейшей визуальной форме. [1] Она представляет интерес, поскольку , по-видимому, является простейшей связью, обладающей свойством Брунна — связью связанных компонентов, которая при удалении одного компонента становится полностью несвязанной [2] — за исключением колец Борромео с шестью пересечениями . [3]

Другими словами, никакие две петли не связаны друг с другом напрямую , но все три связаны между собой, поэтому удаление любой петли освобождает две другие. На изображении в информационном поле справа красная петля не связана ни с синей, ни с желтой петлей, и если красная петля удалена, то синюю и желтую петли также можно распутать друг с другом, не разрезая ни одну из них.

Согласно работе Славика В. Яблана , связь L10a140 можно рассматривать как вторую в бесконечной серии связей Брунна, начинающихся с колец Борромео. Таким образом, если синяя и желтая петли имеют только один поворот вдоль каждой стороны, результирующая конфигурация — это кольца Борромео; если синяя и желтая петли имеют три поворота вдоль каждой стороны, результирующая конфигурация — это связь L10a140; если синяя и желтая петли имеют пять поворотов вдоль каждой стороны, результирующая конфигурация — это связь из трех петель с 14 общими пересечениями и т. д. и т. п. [4]

Инварианты

Многомерный полином Александера для связи L10a140 равен

Δ ( ты , в , ж ) = ( ты − 1 ) ( в − 1 ) ( ж − 1 ) ( в ж + 1 ) 2 в ж ты в ж , {\displaystyle \Delta (u,v,w)={\frac {(u-1)(v-1)(w-1)(vw+1)^{2}}{vw{\sqrt {uvw}}}},\,}

полином Конвея — это

∇ ( з ) = 4 з 4 + 4 з 6 + з 8 , {\displaystyle \nabla (z)=4z^{4}+4z^{6}+z^{8},\,}

многочлен Джонса хорошо разлагается на такие факторы, как

В ( т ) = − т 5 + 3 т 4 − 5 т 3 + 8 т 2 − 9 т + 12 − 9 т − 1 + 8 т − 2 − 5 т − 3 + 3 т − 4 − т − 5 = − 1 т 5 ( т 5 − 2 т 4 + т 3 − 2 т 2 + т − 1 ) ( т 5 − т 4 + 2 т 3 − т 2 + 2 т − 1 ) = ж ( т ) ж ( 1 / т ) , {\displaystyle {\begin{aligned}V(t)&=-t^{5}+3t^{4}-5t^{3}+8t^{2}-9t+12-9t^{-1}+8t^{-2}-5t^{-3}+3t^{-4}-t^{-5}\\[8pt]&=-{\frac {1}{t^{5}}}\left(t^{5}-2t^{4}+t^{3}-2t^{2}+t-1\right)\left(t^{5}-t^{4}+2t^{3}-t^{2}+2t-1\right)\\[8pt]&=w(t)w(1/t),\,\end{aligned}}}

где (Обратите внимание, что это по сути полином Джонса для связи Уайтхеда .) ж ( т ) = т 5 − 2 т 4 + т 3 − 2 т 2 + т − 1. {\displaystyle w(t)=t^{5}-2t^{4}+t^{3}-2t^{2}+t-1.} ж ( т ) {\displaystyle w(т)}

Полином HOMFLY равен

П ( α , з ) = з − 2 α − 2 − 4 з 2 α − 2 − 4 з 4 α − 2 − з 6 α − 2 − 2 з − 2 + 8 з 2 + 12 з 4 + 6 з 6 + з 8 + з − 2 α 2 − 4 з 2 α 2 − 4 з 4 α 2 − з 6 α 2 , {\displaystyle P(\alpha,z)=z^{-2}\alpha ^{-2}-4z^{2}\alpha ^{-2}-4z^{4}\alpha ^{-2}-z^{6}\alpha ^{-2}-2z^{-2}+8z^{2}+12z^{4}+6z^{6}+z^{8}+z^{-2}\alpha ^{2}-4z^{2}\alpha ^{2}-4z^{4}\alpha ^{2}-z^{6}\alpha ^{2},\,}

и полином Кауфмана равен

Ф ( а , з ) = 1 + 2 з − 2 + а − 2 з − 2 + а 2 з − 2 − 2 а − 1 з − 1 − а з − 1 − 20 з 2 + 2 а − 4 з 2 − 8 а − 2 з 2 − 8 а 2 з 2 + 2 а 4 з 4 + 2 а 4 з 2 − 2 а − 5 з 3 + 4 а − 3 з 3 + 6 а − 1 з 3 + 6 а з 3 + 4 а 3 з 3 − 2 а 5 з 3 + 42 з 4 − 7 а − 4 з 4 + 14 а − 2 з 4 + 14 а 2 з 4 − 7 а 4 з 4 + а − 5 з 5 − 9 а − 3 з 5 − 2 а − 1 з 5 − 2 а з 5 − 9 а 3 з 5 + а 5 з 5 − 28 з 6 + 3 а − 4 з 6 − 11 а − 2 з 6 − 11 а 2 з 6 + 3 а 4 з 6 + 4 а − 3 з 7 − 2 а − 1 з 7 − 2 а з 7 + 4 а 3 з 7 + 8 з 8 + 4 а − 2 з 8 + 4 а 2 з 8 + 2 а − 1 з 9 + 2 а з 9 . {\displaystyle {\begin{aligned}F(a,z)&=1+2z^{-2}+a^{-2}z^{-2}+a^{2}z^{-2}-2a^{-1}z^{-1 }-az^{-1}-20z^{2}+2a^{-4}z^{2}\\[6pt]&{}-8a^{-2}z^{2}-8a^{2}z^{2}+2a^{4} z^{4}+2a^{4}z^{2}-2a^{-5}z^{3}+4a^{-3}z^{3}+6a^{-1}z^{3}\\[6pt]&{}+6az^{ 3}+4a^{3}z^{3}-2a^{5}z^{3}+42z^{4}-7a^{-4}z^{4}+14a^{-2}z^{4}\\[6pt]&{}+ 14a^{2}z^{4}-7a^{4}z^{4}+a^{-5}z^{5}-9a^{-3}z^{5}-2a^{-1}z^{5}-2az^{5}-9 a^{3}z^{5}\\[6pt]&{}+a^{5}z^{5}-28z^{6}+3a^{-4}z^{6}-11a^{-2}z^{6}-11a^{ 2}z^{6}+3a^{4}z^{6}+4a^{-3}z^{7}\\[6pt]&{}-2a^{-1}z^{7}-2az^{7}+4a^{3}z^ {7}+8z^{8}+4a^{-2}z^{8}+4a^{2}z^{8}+2a^{-1}z^{9}+2az^{9}.\end{aligned}}}

Псевдосимметричные визуальные варианты

Дэвид Сварт [5] и независимо Рик Мабри и Лора МакКормик [6] обнаружили альтернативные 12-пересекающиеся визуальные представления связи L10a140. В этих изображениях связь больше не имеет строго чередующихся пересечений (как в ее простейшей 10-пересекающейся форме), но имеет большую поверхностную симметрию.

Итак, самое левое изображение ниже показывает 12-перекрестную связь (отличную как от колец Борромео, так и от связи L10a140) с шестикратной вращательной симметрией. Центральное изображение показывает похожее изображение связи L10a140 (но без истинной вращательной симметрии). Аналогично, самое правое изображение показывает изображение связи L10a140 с поверхностной четырехкратной симметрией.

  • Полностью симметричное 12-пересекающееся брунновское зацепление (L12a1882)
    Полностью симметричное 12-пересекающееся брунновское зацепление (L12a1882)
  • L10a140 в псевдо 6-симметричной форме
    L10a140 в псевдо 6-симметричной форме
  • L10a140 в псевдо 4-симметричной форме
    L10a140 в псевдо 4-симметричной форме

Ссылки

  1. ^ "L10a140", Атлас узлов .
  2. ^ Адамс, Колин С. (1994). Книга об узлах , [ нужная страница ] . Американское математическое общество. ISBN  9780716723936 .
  3. ^ Бар-Натан, Дрор (16 августа 2010 г.). «Все бруннийцы, возможно», Академический Омут Мысли .
  4. ^ Jablan, Slavik V., Are Borromean Links So Rare? , Forma 14 (1999), 269–277. Онлайн в электронном журнале Vismath . L10a140 изображен на среднем рисунке верхнего изображения.
  5. ^ Дрор Бар-Натан (2010-08-14). «Ссылка от Дэвида Сварта», [Академический Омут памяти] .
  6. ^ Сварт, Дэвид (апрель 2011 г.). «Это то, что есть». Math Horizons . 18 (4).
На Wikimedia Commons есть медиафайлы по теме L10a140 .
  • «Это то, что есть», Flickr.com .
Взято с "https://en.wikipedia.org/w/index.php?title=L10a140_link&oldid=1223525220"