3 21 многогранник
 3 21            |  2 31            |  1 32            | |||
 Исправлено 3 21            |  биректифицированный 3 21            | ||||
 Исправлено 2 31            |  Исправлено 1 32            | ||||
| Ортогональные проекции в плоскости Коксетера E 7 | |||||
|---|---|---|---|---|---|
В 7-мерной геометрии многогранник 3 21 является однородным 7-мерным многогранником , построенным в рамках симметрии группы E 7. Он был открыт Торолдом Госсетом и опубликован в его статье 1900 года. Он назвал его 7-мерной полуправильной фигурой . [1]
Его символ Коксетера — 3 21 , описывающий его бифуркационную диаграмму Коксетера-Дынкина с одним кольцом на конце одной из последовательностей из 3 узлов.
Выпрямленный 3 21 строится по точкам в средних ребрах 3 21. Двуспрямленный 3 21 строится по точкам в центрах треугольных граней 3 21. Триспрямленный 3 21 строится по точкам в тетраэдрических центрах 3 21 и совпадает с выпрямленным 1 32 .
Эти многогранники являются частью семейства из 127 (2 7 -1) выпуклых однородных многогранников в 7-мерном пространстве , состоящих из однородных граней и вершинных фигур 6-многогранников , определяемых всеми перестановками колец в этой диаграмме Коксетера-Дынкина :









 .
.
321многогранник
| 3 21 многогранник | |
|---|---|
| Тип | Однородный 7-многогранник |
| Семья | многогранник k 21 |
| Символ Шлефли | {3,3,3,3 2,1 } |
| символ Коксетера | 3 21 |
| Диаграмма Коксетера |            |
| 6-гранный | 702 всего: 126 3 11  576 {3 5 }  |
| 5-гранный | 6048: 4032 {3 4 }  2016 {3 4 }  |
| 4-х гранный | 12096 {3 3 } |
| Клетки | 10080 {3,3} |
| Лица | 4032 {3} |
| Края | 756 |
| Вершины | 56 |
| Вершинная фигура | 2 21 многогранник |
| Петри полигон | октадекагон |
| Группа Коксетера | Е 7 , [3 3,2,1 ], заказ 2903040 |
| Характеристики | выпуклый |
В 7-мерной геометрии многогранник 3 21 является однородным многогранником . Он имеет 56 вершин и 702 грани: 126 3 11 и 576 6-симплексов .
Для визуализации этот 7-мерный многогранник часто отображается в специальном наклонном ортографическом направлении проекции, которое вписывает его 56 вершин в 18-угольный правильный многоугольник (называемый многоугольником Петри ). Его 756 ребер нарисованы между 3 кольцами по 18 вершин и 2 вершинами в центре. Определенные высшие элементы (грани, ячейки и т. д.) также могут быть извлечены и нарисованы на этой проекции.
1- скелет многогранника 3 21 представляет собой граф Госсета .
Этот многогранник, наряду с 7-симплексом , может замостить 7-мерное пространство, представленное 3 31 и диаграммой Коксетера-Дынкина:







 .
.
Альтернативные названия
- Его также называют многогранником Гесса по имени Эдмунда Гесса, который его впервые открыл.
- Он был перечислен Торольдом Госсетом в его статье 1900 года. Он назвал его 7-ic полуправильной фигурой . [1]
- Э. Л. Элте назвал его V 56 (из-за 56 вершин) в своем списке полуправильных многогранников 1912 года. [2]
- HSM Коксетер назвал его 3 21 из-за его бифурцирующей диаграммы Коксетера-Дынкина , имеющей 3 ветви длиной 3, 2 и 1, и имеющую одно кольцо на конечном узле 3 ветви.
- Гекатоникосигекса-пентакосигептаконтигекса-экзон (сокращение Naq) - 126-576 фасетный полиэкзон (Джонатан Бауэрс) [3]
Координаты
56 вершин можно проще всего представить в 8-мерном пространстве, получив 28 перестановок координат и их противоположностей:
- ± (-3, -3, 1, 1, 1, 1, 1, 1)
Строительство
Его конструкция основана на группе E7 . Коксетер назвал его 3 21 по его бифурцирующей диаграмме Коксетера-Дынкина с одним кольцом на конце последовательности из 3 узлов.
Информацию о фасетах можно извлечь из диаграммы Коксетера-Дынкина ,









 .
.
Удаление узла на короткой ветви оставляет 6-симплекс ,









 .
.
Удаление узла на конце ветви длиной 2 оставляет 6-ортоплекс в его измененной форме: 3 11 ,







 .
.
Каждая симплексная грань касается 6-ортоплексной грани, в то время как чередующиеся грани ортоплекса касаются либо симплекса, либо другого ортоплекса.
Вершинная фигура определяется путем удаления окольцованного узла и окольцования соседнего узла. Это дает 2 21 многогранник,







 .
.
Рассматривая матрицу конфигурации , количество элементов можно получить путем удаления зеркал и отношений порядков групп Кокстера . [4]
| Е 7 |            | к -лицо | ф к | ф 0 | ф 1 | ф 2 | ф 3 | ф 4 | ф 5 | ф 6 | k -цифры | примечания | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Е 6 |            | ( ) | ф 0 | 56 | 27 | 216 | 720 | 1080 | 432 | 216 | 72 | 27 | 2 21 | Е 7 /Е 6 = 72x8!/72x6! = 56 |
| Д 5 А 1 |            | { } | ф 1 | 2 | 756 | 16 | 80 | 160 | 80 | 40 | 16 | 10 | 5-демикуб | Э 7 /Д 5 А 1 = 72x8!/16/5!/2 = 756 |
| А 4 А 2 |            | {3} | ф 2 | 3 | 3 | 4032 | 10 | 30 | 20 | 10 | 5 | 5 | выпрямленный 5-элементный | Е 7 /А 4 А 2 = 72x8!/5!/2 = 4032 |
| А 3 А 2 А 1 |            | {3,3} | ф 3 | 4 | 6 | 4 | 10080 | 6 | 6 | 3 | 2 | 3 | треугольная призма | Э 7 /А 3 А 2 А 1 = 72x8!/4!/3!/2 = 10080 |
| А 4 А 1 |            | {3,3,3} | ф 4 | 5 | 10 | 10 | 5 | 12096 | 2 | 1 | 1 | 2 | равнобедренный треугольник | Е 7 /А 4 А 1 = 72x8!/5!/2 = 12096 |
| А 5 А 1 |            | {3,3,3,3} | ф 5 | 6 | 15 | 20 | 15 | 6 | 4032 | * | 1 | 1 | { } | Е 7 /А 5 А 1 = 72x8!/6!/2 = 4032 |
| А 5 |            | 6 | 15 | 20 | 15 | 6 | * | 2016 | 0 | 2 | Э 7 /А 5 = 72x8!/6! = 2016 | |||
| А 6 |            | {3,3,3,3,3} | ф 6 | 7 | 21 | 35 | 35 | 21 | 10 | 0 | 576 | * | ( ) | Э 7 /А 6 = 72x8!/7! = 576 |
| Д 6 |            | {3,3,3,3,4} | 12 | 60 | 160 | 240 | 192 | 32 | 32 | * | 126 | Э 7 /Д 6 = 72x8!/32/6! = 126 | ||
Изображения
| Е7 | Е6 / Ф4 | В7/А6 |
|---|---|---|
 [18] | 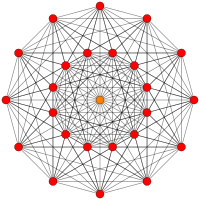 [12] | 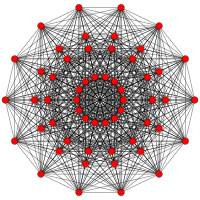 [7x2] |
| А5 | Д7/Б6 | Д6/Б5 |
 [6] |  [12/2] |  [10] |
| Д5 / В4 / А4 | Д4 / В3 / А2 / Г2 | Д3 / В2 / А3 |
 [8] |  [6] |  [4] |
Связанные многогранники
3 21 является пятым в размерной серии полуправильных многогранников . Каждый прогрессивный однородный многогранник строится из вершинной фигуры предыдущего многогранника. Торольд Госсет определил эту серию в 1900 году как содержащую все грани правильного многогранника , содержащую все симплексы и ортоплексы .
| k 21 фигура в n измерениях | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Космос | Конечный | Евклидов | Гиперболический | ||||||||
| Е н | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |||
Группа Коксетера | Э 3 =А 2 А 1 | Э 4 =А 4 | Э 5 =Д 5 | Е 6 | Е 7 | Е 8 | Э 9 = = Э 8 + | Е 10 = = Е 8 ++ | |||
Диаграмма Коксетера |      |      |        |          |            |              |                |                  | |||
| Симметрия | [3 −1,2,1 ] | [3 0,2,1 ] | [3 1,2,1 ] | [3 2,2,1 ] | [3 3,2,1 ] | [3 4,2,1 ] | [3 5,2,1 ] | [3 6,2,1 ] | |||
| Заказ | 12 | 120 | 1,920 | 51,840 | 2,903,040 | 696,729,600 | ∞ | ||||
| График |  |  |  |  |  |  | - | - | |||
| Имя | −1 21 | 0 21 | 1 21 | 2 21 | 321 | 4 21 | 5 21 | 6 21 | |||
Он находится в размерной серии однородных многогранников и сот, выраженной Коксетером как серия 3 k1 . (Вырожденный 4-мерный случай существует как 3-сферная мозаика, тетраэдральный осоэдр .)
| Космос | Конечный | Евклидов | Гиперболический | |||
|---|---|---|---|---|---|---|
| н | 4 | 5 | 6 | 7 | 8 | 9 |
Группа Коксетера | А 3 А 1 | А 5 | Д 6 | Е 7 | =Э 7 + | =Э 7 ++ |
Диаграмма Коксетера |        |        |          |            |              |                |
| Симметрия | [3 −1,3,1 ] | [3 0,3,1 ] | [[3 1,3,1 ]] = [4,3,3,3,3] | [3 2,3,1 ] | [3 3,3,1 ] | [3 4,3,1 ] |
| Заказ | 48 | 720 | 46,080 | 2,903,040 | ∞ | |
| График |  |  |  | - | - | |
| Имя | 3 1,-1 | 3 10 | 3 11 | 321 | 3 31 | 341 |
Исправлено 321многогранник
| Выпрямленный 3 21 многогранник | |
|---|---|
| Тип | Однородный 7-многогранник |
| Символ Шлефли | т 1 {3,3,3,3 2,1 } |
| символ Коксетера | т 1 (3 21 ) |
| Диаграмма Коксетера |            |
| 6-гранный | 758 |
| 5-гранный | 44352 |
| 4-х гранный | 70560 |
| Клетки | 48384 |
| Лица | 11592 |
| Края | 12096 |
| Вершины | 756 |
| Вершинная фигура | 5-демикубовая призма |
| Петри полигон | октадекагон |
| Группа Коксетера | Е 7 , [3 3,2,1 ], заказ 2903040 |
| Характеристики | выпуклый |
Альтернативные названия
- Выпрямленный гекатоникосигекса-пентакосигептаконтигекса-экзон как выпрямленный 126-576 фасетный полиэкзон (аббревиатура ranq) (Джонатан Бауэрс) [5]
Строительство
Его конструкция основана на группе E7 . Коксетер назвал его 3 21 по его бифурцирующей диаграмме Коксетера-Дынкина с одним узлом на конце последовательности из 3 узлов.
Информацию о фасетах можно извлечь из диаграммы Коксетера-Дынкина ,









 .
.
Удаление узла на короткой ветви оставляет 6-симплекс ,









 .
.
Удаление узла на конце ветви длиной 2 оставляет выпрямленный 6-ортоплекс в его измененной форме: t 1 3 11 ,







 .
.
Удаление узла на конце ветви длиной 3 оставляет 2 21 ,







 .
.
Вершинная фигура определяется путем удаления окольцованного узла и окольцования соседнего узла. Это делает призму 5-демикуб ,







 .
.
Изображения
| Е7 | Е6 / Ф4 | В7/А6 |
|---|---|---|
 [18] |  [12] |  [7x2] |
| А5 | Д7/Б6 | Д6/Б5 |
 [6] | 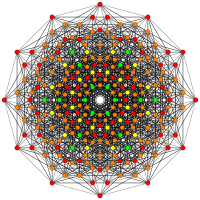 [12/2] | 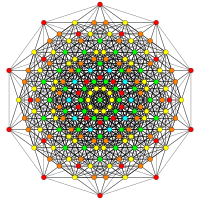 [10] |
| Д5 / В4 / А4 | Д4 / В3 / А2 / Г2 | Д3 / В2 / А3 |
 [8] | 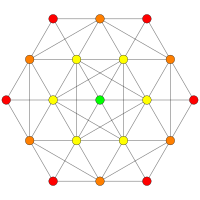 [6] | 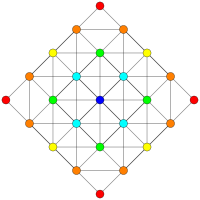 [4] |
Двукратно исправленный 321многогранник
| Двуспрямленный многогранник 3 21 | |
|---|---|
| Тип | Однородный 7-многогранник |
| Символ Шлефли | т 2 {3,3,3,3 2,1 } |
| символ Коксетера | т 2 (3 21 ) |
| Диаграмма Коксетера |            |
| 6-гранный | 758 |
| 5-гранный | 12348 |
| 4-х гранный | 68040 |
| Клетки | 161280 |
| Лица | 161280 |
| Края | 60480 |
| Вершины | 4032 |
| Вершинная фигура | 5-клеточная треугольная дуопризма |
| Петри полигон | октадекагон |
| Группа Коксетера | Е 7 , [3 3,2,1 ], заказ 2903040 |
| Характеристики | выпуклый |
Альтернативные названия
- Двукратно ректифицированный гекатоникосигекса-пентакосигептаконтигекса-экзон как двукратно ректифицированный 126-576 фасетный полиэкзон (аббревиатура branq) (Джонатан Бауэрс) [6]
Строительство
Его конструкция основана на группе E7 . Коксетер назвал его 3 21 по его бифурцирующей диаграмме Коксетера-Дынкина с одним узлом на конце последовательности из 3 узлов.
Информацию о фасетах можно извлечь из диаграммы Коксетера-Дынкина ,









 .
.
Удаление узла на короткой ветви оставляет биректифицированный 6-симплекс ,









 .
.
Удаление узла на конце ветви длиной 2 оставляет биректифицированный 6-ортоплекс в его измененной форме: t 2 (3 11 ) ,







 .
.
Удаление узла на конце ветви длиной 3 оставляет выпрямленный многогранник 2 21 в его альтернативной форме: t 1 (2 21 ) ,







 .
.
Вершинная фигура определяется путем удаления окольцованного узла и окольцования соседнего узла. Это дает выпрямленную 5-клеточную -треугольную дуопризму,







 .
.
Изображения
| Е7 | Е6 / Ф4 | В7/А6 |
|---|---|---|
 [18] |  [12] |  [7x2] |
| А5 | Д7/Б6 | Д6/Б5 |
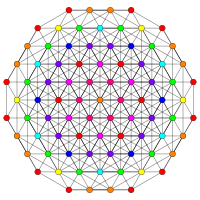 [6] |  [12/2] |  [10] |
| Д5 / В4 / А4 | Д4 / В3 / А2 / Г2 | Д3 / В2 / А3 |
 [8] |  [6] | 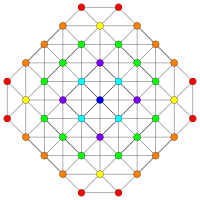 [4] |
Смотрите также
Примечания
- ^ ab Госсет, 1900
- ^ Элте, 1912
- ^ Клитцинг, (o3o3o3o *c3o3o3x - naq)
- ^ Коксетер, Регулярные многогранники, 11.8 Фигуры Госсета в шести, семи и восьми измерениях, стр. 202-203
- ^ Клитцинг. (o3o3o3o *c3o3x3o - ранк)
- ^ Клитцинг, (o3o3o3o *c3x3o3o - branq)
Ссылки
- Т. Госсет : О правильных и полуправильных фигурах в пространстве n измерений , Вестник математики, Макмиллан, 1900
- Элте, Э.Л. (1912), Полуправильные многогранники гиперпространств , Гронинген: Университет Гронингена
- HSM Coxeter, Правильные многогранники , 3-е издание, Довер, Нью-Йорк, 1973
- Калейдоскопы: избранные труды Х. С. М. Коксетера , под редакцией Ф. Артура Шерка, Питера МакМаллена, Энтони К. Томпсона, Азии Айвик Вайс, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
- (Документ 24) HSM Coxeter, Regular and Semi-Regular Polytopes III , [Math. Zeit. 200 (1988) 3-45] См. стр. 342 (рисунок 3.7c) Питера МакМаллена: (18-угольный граф узлов и ребер 3 21 )
- Клитцинг, Ричард. «7D однородные многогранники (полиексы)».o3o3o3o *c3o3o3x - naq, o3o3o3o *c3o3x3o - ranq, o3o3o3o *c3x3o3o - branq
Внешние ссылки
- Многогранники Госсета в vZome


