Химическое равновесие
| Часть серии статей о |
| Химия |
|---|
 |
|
В химической реакции химическое равновесие — это состояние, в котором как реагенты , так и продукты присутствуют в концентрациях , которые не имеют дальнейшей тенденции к изменению со временем, так что нет никаких наблюдаемых изменений в свойствах системы . [ 1] Это состояние возникает, когда прямая реакция протекает с той же скоростью, что и обратная реакция . Скорости реакции прямой и обратной реакции, как правило, не равны нулю, но они равны. Таким образом, нет чистых изменений в концентрациях реагентов и продуктов. Такое состояние известно как динамическое равновесие . [2] [3]
Историческое введение
Концепция химического равновесия была разработана в 1803 году после того, как Бертолле обнаружил , что некоторые химические реакции обратимы . [4] Для того чтобы любая реакционная смесь существовала в равновесии, скорости прямой и обратной (обратной) реакции должны быть равны. В следующем химическом уравнении стрелки указывают в обоих направлениях, чтобы обозначить равновесие. [5] A и B — это химические виды реагентов , S и T — это виды продуктов, а α , β , σ и τ — стехиометрические коэффициенты соответствующих реагентов и продуктов:
- α А + β В ⇌ σ S + τ Т
Говорят, что равновесное положение концентрации реакции лежит «далеко справа», если при равновесии почти все реагенты израсходованы. И наоборот, говорят, что равновесное положение находится «далеко слева», если из реагентов почти не образуется никаких продуктов.
Гульдберг и Вааге (1865), развивая идеи Бертолле, предложили закон действия масс :
где A, B, S и T — активные массы , а k + и k − — константы скорости . Поскольку в равновесии скорости вперед и назад равны:
и отношение констант скорости также является константой, теперь известной как константа равновесия .
По соглашению, продукты образуют числитель . Однако закон действующих масс действителен только для согласованных одностадийных реакций, которые протекают через одно переходное состояние , и недействителен в общем случае, поскольку уравнения скорости в общем случае не следуют стехиометрии реакции, как предполагали Гульдберг и Вааге (см., например, нуклеофильное алифатическое замещение S N 1 или реакцию водорода и брома с образованием бромистого водорода ). Однако равенство скоростей прямой и обратной реакции является необходимым условием химического равновесия, хотя его недостаточно для объяснения того, почему равновесие происходит.
Несмотря на ограничения этого вывода, константа равновесия для реакции действительно является константой, независимой от активности различных участвующих видов, хотя она зависит от температуры, как это наблюдается в уравнении Вант-Гоффа . Добавление катализатора повлияет как на прямую, так и на обратную реакцию одинаково и не повлияет на константу равновесия. Катализатор ускорит обе реакции, тем самым увеличивая скорость достижения равновесия. [2] [6]
Хотя макроскопические равновесные концентрации постоянны во времени, реакции происходят на молекулярном уровне. Например, в случае уксусной кислоты, растворенной в воде и образующей ацетат и гидроксоний ионы,
- СН 3 СО 2 Н + Н 2 О ⇌ СН 3 СО−2+ Н 3 О +
протон может перепрыгнуть с одной молекулы уксусной кислоты на молекулу воды, а затем на ацетат-анион, образуя другую молекулу уксусной кислоты и оставляя число молекул уксусной кислоты неизменным. Это пример динамического равновесия . Равновесия, как и остальная часть термодинамики, являются статистическими явлениями, средними значениями микроскопического поведения.
Принцип Ле Шателье (1884) предсказывает поведение равновесной системы, когда происходят изменения условий ее реакции. Если динамическое равновесие нарушается изменением условий, положение равновесия перемещается, частично обращая изменение . Например, добавление большего количества S (к химической реакции выше) извне вызовет избыток продуктов, и система попытается противодействовать этому, увеличивая обратную реакцию и отодвигая точку равновесия назад (хотя константа равновесия останется прежней).
Если к смеси уксусной кислоты добавить минеральную кислоту , увеличивая концентрацию иона гидроксония, то количество диссоциации должно уменьшаться, поскольку реакция движется влево в соответствии с этим принципом. Это также можно вывести из выражения константы равновесия для реакции:
Если {H 3 O + } увеличивается, {CH 3 CO 2 H} должен увеличиваться и CH 3 CO−2должна уменьшаться. H 2 O исключается, так как она является растворителем и ее концентрация остается высокой и почти постоянной.
Дж. У. Гиббс предположил в 1873 году, что равновесие достигается, когда «доступная энергия» (теперь известная как свободная энергия Гиббса или энергия Гиббса) системы достигает своего минимального значения, предполагая, что реакция проводится при постоянной температуре и давлении. Это означает, что производная энергии Гиббса по координате реакции (мера степени произошедшей реакции , варьирующаяся от нуля для всех реагентов до максимума для всех продуктов) исчезает (потому что dG = 0), сигнализируя о стационарной точке . Эта производная называется энергией Гиббса реакции (или изменением энергии) и соответствует разнице между химическими потенциалами реагентов и продуктов в составе реакционной смеси. [1] Этот критерий является как необходимым, так и достаточным. Если смесь не находится в равновесии, высвобождение избыточной энергии Гиббса (или энергии Гельмгольца при реакциях с постоянным объемом) является «движущей силой» для изменения состава смеси до достижения равновесия. Константу равновесия можно связать со стандартным изменением свободной энергии Гиббса для реакции с помощью уравнения
где R — универсальная газовая постоянная , а T — температура .
Когда реагенты растворяются в среде с высокой ионной силой, отношение коэффициентов активности можно считать постоянным. В этом случае отношение концентрации , K c ,
где [A] — концентрация A и т. д., не зависит от аналитической концентрации реагентов. По этой причине константы равновесия для растворов обычно определяются в средах с высокой ионной силой. K c изменяется в зависимости от ионной силы , температуры и давления (или объема). Аналогично K p для газов зависит от парциального давления . Эти константы легче измерить, и они встречаются в курсах химии средней школы.
Термодинамика
При постоянной температуре и давлении необходимо учитывать свободную энергию Гиббса , G , тогда как при постоянной температуре и объеме необходимо учитывать свободную энергию Гельмгольца , A , для реакции; а при постоянной внутренней энергии и объеме необходимо учитывать энтропию, S , для реакции.
Случай постоянного объема важен в геохимии и атмосферной химии , где изменения давления значительны. Обратите внимание, что если бы реагенты и продукты находились в стандартном состоянии (полностью чистые), то не было бы обратимости и равновесия. Действительно, они обязательно занимали бы непересекающиеся объемы пространства. Смешение продуктов и реагентов вносит большой рост энтропии (известный как энтропия смешивания ) в состояния, содержащие равную смесь продуктов и реагентов, и приводит к отличительному минимуму в энергии Гиббса как функции степени реакции. [7] Стандартное изменение энергии Гиббса вместе с энергией Гиббса смешивания определяют состояние равновесия. [8] [9]
В этой статье рассматривается только случай постоянного давления . Связь между свободной энергией Гиббса и константой равновесия можно найти, рассматривая химические потенциалы . [1]
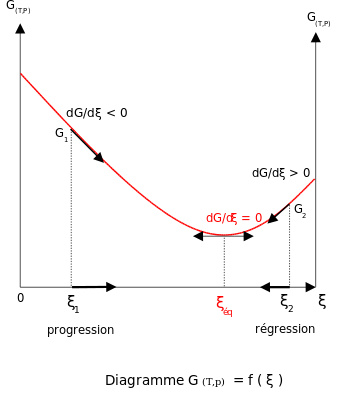
При постоянной температуре и давлении в отсутствие приложенного напряжения свободная энергия Гиббса , G , для реакции зависит только от степени реакции : ξ (греческая буква xi ), и может только уменьшаться согласно второму закону термодинамики . Это означает, что производная G по ξ должна быть отрицательной, если реакция происходит; в равновесии эта производная равна нулю.
- : равновесие
Для того чтобы удовлетворить термодинамическому условию равновесия, энергия Гиббса должна быть стационарной, что означает, что производная G по степени реакции, ξ , должна быть равна нулю. Можно показать, что в этом случае сумма химических потенциалов , умноженная на стехиометрические коэффициенты продуктов, равна сумме тех, которые соответствуют реагентам. [10] Следовательно, сумма энергий Гиббса реагентов должна быть равна сумме энергий Гиббса продуктов.
где μ в данном случае — парциальная молярная энергия Гиббса, химический потенциал . Химический потенциал реагента A является функцией активности , {A} этого реагента.
(где μо
А— стандартный химический потенциал ).
Определение уравнения энергии Гиббса взаимодействует с фундаментальным термодинамическим соотношением, давая
- .
Подстановка dN i = ν i dξ в приведенное выше уравнение дает стехиометрический коэффициент ( ) и дифференциал, который обозначает реакцию, происходящую в бесконечно малой степени ( dξ ). При постоянном давлении и температуре приведенные выше уравнения можно записать как
что является изменением свободной энергии Гиббса для реакции. Это приводит к:
- .
Подставляя химические потенциалы:
- ,
отношение становится:
- :
что является стандартным изменением энергии Гиббса для реакции , которое можно рассчитать с помощью термодинамических таблиц. Коэффициент реакции определяется как:
Поэтому,
В состоянии равновесия:
приводит к:
и
Получение значения стандартного изменения энергии Гиббса позволяет рассчитать константу равновесия.
Добавление реагентов или продуктов
Для реакционной системы в состоянии равновесия: Q r = K eq ; ξ = ξ eq .
- Если активность компонентов изменяется, то значение коэффициента реакции изменяется и становится отличным от константы равновесия: Q r ≠ K eq и тогда
- Если активность реагента i увеличивается, то коэффициент реакции уменьшается. Тогда и Реакция сместится вправо (т.е. в прямом направлении, и, таким образом, будет образовываться больше продуктов).
- Если активность продукта j увеличивается, то и реакция сместится влево (т.е. в обратном направлении, и, следовательно, продуктов будет образовываться меньше).
Обратите внимание, что активность и константы равновесия являются безразмерными числами.
Обработка активности
Выражение для константы равновесия можно переписать как произведение коэффициента концентрации K c и коэффициента активности Γ .
[A] — концентрация реагента A и т. д. В принципе возможно получить значения коэффициентов активности γ. Для растворов могут использоваться уравнения, такие как уравнение Дебая-Хюккеля или расширения, такие как уравнение Дэвиса [11], теория взаимодействия специфических ионов или уравнения Питцера [12] . Однако это не всегда возможно. Обычно принято считать, что Γ — константа, и использовать коэффициент концентрации вместо термодинамической константы равновесия. Также общепринято использовать термин константа равновесия вместо более точного коэффициента концентрации . Эта практика будет соблюдаться здесь.
Для реакций в газовой фазе вместо концентрации используется парциальное давление , а вместо коэффициента активности — коэффициент летучести . В реальном мире, например, при производстве аммиака в промышленности, необходимо учитывать коэффициенты летучести. Летучесть, f , является произведением парциального давления и коэффициента летучести. Химический потенциал вида в реальной газовой фазе определяется как
поэтому общее выражение, определяющее константу равновесия, справедливо как для растворов, так и для газовых фаз. [ необходима ссылка ]
Коэффициенты концентрации
В водном растворе константы равновесия обычно определяются в присутствии «инертного» электролита, такого как нитрат натрия , NaNO 3 или перхлорат калия , KClO 4. Ионная сила раствора определяется как
где c i и z i обозначают концентрацию и ионный заряд иона типа i , а сумма берется по всем N типам заряженных видов в растворе. Когда концентрация растворенной соли намного выше аналитических концентраций реагентов, ионы, происходящие из растворенной соли, определяют ионную силу, и ионная сила фактически постоянна. Поскольку коэффициенты активности зависят от ионной силы, коэффициенты активности видов фактически независимы от концентрации. Таким образом, предположение о том, что Γ является постоянным, оправдано. Концентрационный коэффициент является простым кратным константы равновесия. [13]
Однако K c будет меняться в зависимости от ионной силы. Если измерять его при серии различных ионных сил, значение можно экстраполировать к нулевой ионной силе. [12] Концентрационный коэффициент, полученный таким образом, парадоксальным образом известен как термодинамическая константа равновесия.
Перед использованием опубликованного значения константы равновесия в условиях ионной силы, отличных от условий, использованных при ее определении, это значение следует скорректировать.
Метастабильные смеси
Смесь может казаться не имеющей тенденции к изменению, хотя она не находится в равновесии. Например, смесь SO 2 и O 2 является метастабильной , поскольку существует кинетический барьер для образования продукта SO 3 .
- 2SO2 + O2 ⇌ 2SO3
Барьер можно преодолеть, если в смеси также присутствует катализатор , как в контактном процессе , но катализатор не влияет на равновесные концентрации.
Аналогично, образование бикарбоната из углекислого газа и воды происходит очень медленно при нормальных условиях.
- CO2 + 2H2O ⇌ HCO−3+ Н 3 О +
но почти мгновенно в присутствии каталитического фермента карбоангидразы .
Чистые вещества
Когда в равновесиях участвуют чистые вещества (жидкости или твердые тела), их активность не отображается в константе равновесия [14], поскольку их числовые значения считаются равными единице.
Применяя общую формулу для константы равновесия к частному случаю разбавленного раствора уксусной кислоты в воде, получаем
- CH 3 CO 2 H + H 2 O ⇌ CH 3 CO 2 − + H 3 O +
Для всех растворов, кроме очень концентрированных, вода может считаться «чистой» жидкостью, и поэтому ее активность равна единице. Выражение константы равновесия поэтому обычно записывается как
- .
Частным случаем является самоионизация воды.
- 2 Н 2 О ⇌ Н 3 О + + ОН −
Поскольку вода является растворителем и имеет активность, равную единице, константа самоионизации воды определяется как
Совершенно законно записывать [H + ] для концентрации ионов гидроксония , поскольку состояние сольватации протона постоянно (в разбавленных растворах) и, таким образом, не влияет на равновесные концентрации. K w изменяется с изменением ионной силы и/или температуры.
Концентрации H + и OH − не являются независимыми величинами. Чаще всего [OH − ] заменяется на K w [H + ] −1 в выражениях констант равновесия, которые в противном случае включали бы гидроксид-ион .
Твердые вещества также не появляются в выражении константы равновесия, если они считаются чистыми и, таким образом, их активность принимается равной единице. Примером является реакция Будуара : [14]
- 2 CO ⇌ CO 2 + C
для которого уравнение (без твердого углерода) записывается как:
Множественные равновесия
Рассмотрим случай двухосновной кислоты H 2 A. При растворении в воде смесь будет содержать H 2 A, HA − и A 2− . Это равновесие можно разделить на два этапа, в каждом из которых высвобождается один протон.
K 1 и K 2 являются примерами ступенчатых констант равновесия. Общая константа равновесия, β D , является произведением ступенчатых констант.
Обратите внимание, что эти константы являются константами диссоциации , поскольку продукты в правой части выражения равновесия являются продуктами диссоциации. Во многих системах предпочтительнее использовать константы ассоциации.
β 1 и β 2 являются примерами констант ассоциации. Очевидно, β 1 = 1/К 2 и β 2 = 1/β D ; log β 1 = p K 2 и log β 2 = p K 2 + p K 1 [15] Для систем с множественным равновесием см. также: теория реакций ответа .
Влияние температуры
Влияние изменения температуры на константу равновесия определяется уравнением Вант-Гоффа
Таким образом, для экзотермических реакций (ΔH отрицательно ), K уменьшается с ростом температуры, но для эндотермических реакций (ΔH положительно), K увеличивается с ростом температуры. Альтернативная формулировка:
На первый взгляд это кажется средством получения стандартной молярной энтальпии реакции путем изучения изменения K с температурой. На практике, однако, этот метод ненадежен, поскольку распространение ошибок почти всегда дает очень большие ошибки в значениях, рассчитанных таким образом.
Влияние электрических и магнитных полей
Влияние электрического поля на равновесие изучалось, в частности, Манфредом Эйгеном [16] [17] .
Типы равновесия
- N 2 (г) ⇌ N 2 (адсорбированный)
- N 2 (адсорбированный) ⇌ 2 N (адсорбированный)
- H 2 (г) ⇌ H 2 (адсорбированный)
- H 2 (адсорбированный) ⇌ 2 H (адсорбированный)
- N (адсорбированный) + 3 H(адсорбированный) ⇌ NH 3 (адсорбированный)
- NH 3 (адсорбированный) ⇌ NH 3 (г)
Равновесие можно в целом классифицировать как гетерогенное и гомогенное равновесие. [18] Гомогенное равновесие состоит из реагентов и продуктов, принадлежащих к одной и той же фазе, тогда как гетерогенное равновесие вступает в игру для реагентов и продуктов, находящихся в разных фазах.
- В газовой фазе: ракетные двигатели [19]
- Промышленный синтез, например, аммиака в процессе Габера-Боша (изображен справа), происходит посредством последовательности равновесных стадий, включая процессы адсорбции .
- Химия атмосферы
- Морская вода и другие природные воды: химическая океанография
- Распределение между двумя фазами
- Коэффициент распределения log D : важен для фармацевтических препаратов, где липофильность является существенным свойством препарата.
- Жидкостно-жидкостная экстракция , Ионный обмен , Хроматография
- Продукт растворимости
- Поглощение и выделение кислорода гемоглобином в крови
- Кислотно-щелочное равновесие: константа диссоциации кислоты , гидролиз , буферные растворы , индикаторы , кислотно-щелочной гомеостаз
- Комплексообразование металл-лиганд: секвестрирующие агенты , хелатная терапия , контрастные реагенты для МРТ , равновесие Шленка
- Образование аддукта: химия хозяин–гость , супрамолекулярная химия , молекулярное распознавание , тетраоксид диазота
- В некоторых колебательных реакциях приближение к равновесию происходит не асимптотически, а в форме затухающих колебаний. [14]
- Соответствующее уравнение Нернста в электрохимии определяет разницу в электродном потенциале как функцию окислительно-восстановительных концентраций.
- Когда молекулы по обе стороны равновесия способны далее необратимо реагировать во вторичных реакциях, конечное соотношение продуктов определяется в соответствии с принципом Кертина-Гаммета .
В этих приложениях используются такие термины, как константа стабильности, константа образования, константа связывания, константа сродства, константа ассоциации и константа диссоциации. В биохимии принято указывать единицы для констант связывания, которые служат для определения единиц концентрации, используемых при определении значения константы.
Состав смеси
Когда единственным равновесием является образование аддукта 1:1 в составе смеси, существует много способов расчета состава смеси. Например, см. таблицу ICE для традиционного метода расчета pH раствора слабой кислоты.
Существует три подхода к общему расчету состава смеси в состоянии равновесия.
- Самый простой подход заключается в манипулировании различными константами равновесия до тех пор, пока желаемые концентрации не будут выражены через измеренные константы равновесия (эквивалентно измерению химических потенциалов) и начальные условия.
- Минимизировать энергию Гиббса системы. [20] [21]
- Удовлетворить уравнению баланса масс . Уравнения баланса масс — это просто утверждения, которые показывают, что общая концентрация каждого реагента должна быть постоянной по закону сохранения массы .
Уравнения баланса массы
В общем, вычисления довольно сложны или комплексны. Например, в случае двухосновной кислоты, H 2 A, растворенной в воде, два реагента могут быть указаны как сопряженное основание , A 2− , и протон , H + . Следующие уравнения баланса масс могут быть применены в равной степени к основанию, такому как 1,2-диаминоэтан , в этом случае само основание обозначается как реагент A:
где T A — общая концентрация вида A. Обратите внимание, что при написании и использовании этих уравнений принято опускать ионные заряды.
Когда константы равновесия известны и общие концентрации заданы, то есть два уравнения относительно двух неизвестных «свободных концентраций» [A] и [H]. Это следует из того, что [HA] = β 1 [A][H], [H 2 A] = β 2 [A][H] 2 и [OH] = K w [H] −1
поэтому концентрации "комплексов" рассчитываются из свободных концентраций и констант равновесия. Общие выражения, применимые ко всем системам с двумя реагентами, A и B, будут такими:
Легко увидеть, как это можно распространить на три и более реагентов.
Многоосновные кислоты
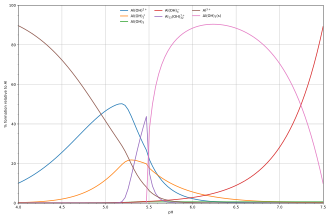
Состав растворов, содержащих реагенты A и H, легко рассчитать как функцию p[H] . Когда [H] известен, свободная концентрация [A] рассчитывается из уравнения баланса масс в A.
Диаграмма рядом показывает пример гидролиза кислоты Льюиса алюминия Al 3+ (aq) [22] показывает концентрации видов для 5 × 10−6 M раствора соли алюминия как функцию pH. Каждая концентрация показана в процентах от общего алюминия.
Растворение и осаждение
Диаграмма выше иллюстрирует момент, когда может образоваться осадок , который не является одним из основных видов в равновесии раствора. При pH чуть ниже 5,5 основными видами, присутствующими в 5 мкМ растворе Al 3+, являются гидроксиды алюминия Al(OH) 2+ , AlOH+2и Al 13 (ОН)7+32, но при повышении pH Al(OH) 3 выпадает в осадок из раствора. Это происходит потому, что Al(OH) 3 имеет очень большую энергию решетки . По мере повышения pH все больше и больше Al(OH) 3 выходит из раствора. Это пример принципа Ле Шателье в действии: увеличение концентрации гидроксид-иона приводит к тому, что больше гидроксида алюминия выпадает в осадок, что удаляет гидроксид из раствора. Когда концентрация гидроксида становится достаточно высокой, растворимый алюминат, Al(OH)−4, формируется.
Другой распространенный случай, когда происходит осаждение, — это когда катион металла взаимодействует с анионным лигандом с образованием электрически нейтрального комплекса. Если комплекс гидрофобный , он выпадет в осадок из воды. Это происходит с ионом никеля Ni 2+ и диметилглиоксимом (dmgH 2 ): в этом случае энергия решетки твердого вещества не особенно велика, но она значительно превышает энергию сольватации молекулы Ni(dmgH) 2 .
Минимизация энергии Гиббса
В состоянии равновесия, при заданной температуре и давлении, а также при отсутствии внешних сил свободная энергия Гиббса G минимальна:
где μ j — химический потенциал молекулярных видов j , а N j — количество молекулярных видов j . Это может быть выражено в терминах термодинамической активности как:
где — химический потенциал в стандартном состоянии, R — газовая постоянная, T — абсолютная температура, A j — активность.
Для закрытой системы никакие частицы не могут войти или выйти, хотя они могут объединяться различными способами. Общее число атомов каждого элемента останется постоянным. Это означает, что минимизация выше должна быть подчинена ограничениям:
где a ij — число атомов элемента i в молекуле j , а b0
я— общее число атомов элемента i , которое является константой, поскольку система замкнута. Если в системе всего k типов атомов, то таких уравнений будет k . Если задействованы ионы, то в матрицу a ij добавляется дополнительная строка , определяющая соответствующий заряд каждой молекулы, который в сумме будет равен нулю.
Это стандартная задача оптимизации , известная как ограниченная минимизация . Наиболее распространенным методом ее решения является использование метода множителей Лагранжа [23] [19] (хотя могут использоваться и другие методы).
Определять:
где λ i — множители Лагранжа, по одному для каждого элемента. Это позволяет рассматривать каждый из N j и λ j независимо, и можно показать с помощью инструментов многомерного исчисления, что условие равновесия задается как
(Для доказательства см. множители Лагранжа .) Это набор ( m + k ) уравнений с ( m + k ) неизвестными ( N j и λ i ) и, следовательно, может быть решен для равновесных концентраций N j , если известны химические активности как функции концентраций при заданной температуре и давлении. (В идеальном случае активности пропорциональны концентрациям.) (См. Термодинамические базы данных для чистых веществ .) Обратите внимание, что второе уравнение является лишь начальными ограничениями для минимизации.
Этот метод расчета равновесных химических концентраций полезен для систем с большим количеством различных молекул. Использование уравнений сохранения k атомных элементов для ограничения массы является простым и заменяет использование уравнений стехиометрических коэффициентов. [19] Результаты согласуются с результатами, указанными химическими уравнениями. Например, если равновесие указано одним химическим уравнением:, [24]
где ν j — стехиометрический коэффициент для j -й молекулы (отрицательный для реагентов, положительный для продуктов), а R j — символ для j -й молекулы, правильно сбалансированное уравнение будет подчиняться:
Умножая первое условие равновесия на ν j и используя приведенное выше уравнение, получаем:
Как и выше, определение ΔG
где K c — константа равновесия , а ΔG будет равна нулю при равновесии.
Аналогичные процедуры существуют для минимизации других термодинамических потенциалов . [19]
Смотрите также
- Ацидоз
- Алкалоз
- Газы артериальной крови
- Метод Бенеши–Хильдебранда
- Определение констант равновесия
- Константа равновесия
- Уравнение Хендерсона – Хассельбаха
- Соотношение массы и действия
- Кинетика Михаэлиса–Ментена
- рСО2
- рН
- п К а
- Окислительно-восстановительные равновесия
- Устойчивое состояние (химия)
- Термодинамические базы данных для чистых веществ
- Неслучайная двухжидкостная модель (модель NRTL) – Расчеты фазового равновесия
- Модель UNIQUAC – расчеты фазового равновесия
Ссылки
- ^ abc Аткинс, Питер; Де Паула, Хулио (2006). Физическая химия Аткинса (8-е изд.). WH Freeman. стр. 200–202. ISBN 0-7167-8759-8.
- ^ ab Atkins, Peter W.; Jones, Loretta (2008). Химические принципы: поиски понимания (2-е изд.). ISBN 978-0-7167-9903-0.
- ^ IUPAC , Compendium of Chemical Terminology , 2nd ed. («Золотая книга») (1997). Онлайн-исправленная версия: (2006–) «химическое равновесие». doi :10.1351/goldbook.C01023
- ^ Бертолле, CL (1803). Essai de statique chimique [ Очерк химической статики ] (на французском языке). Париж, Франция: Фирмен Дидо.На стр. 404–407 Бертелло упоминает, что, когда он сопровождал Наполеона в его экспедиции в Египет, он (Бертелло) посетил озеро Натрон и обнаружил на его берегах карбонат натрия. Он понял, что это продукт обратной обычной реакции Na 2 CO 3 + CaCl 2 → 2NaCl + CaCO 3 ↓ и, следовательно, конечным состоянием реакции является состояние равновесия между двумя противоположными процессами. Из стр. 405 . прибудет время, когда силы уравновесятся». (... разложение хлорида натрия, таким образом, продолжается до тех пор, пока не образуется достаточное количество хлорида кальция, поскольку соляная кислота должна быть разделена между двумя основаниями в соотношении их действия [т.е. способности реагировать]; оно достигает конечной [точки ] при котором их силы уравновешиваются.)
- ↑ Обозначение ⇌ было предложено в 1884 году голландским химиком Якобусом Генрикусом ван 'т Хоффом . См.: van 't Hoff, JH (1884). Études de Dynamique Chemique [ Исследования химической динамики ] (на французском языке). Амстердам, Нидерланды: Frederik Muller & Co. стр. 4– 5.Van 't Hoff назвал реакции, которые не дошли до конца, «ограниченными реакциями». С. 4–5: «Or M. Pfaundler a relieé ces deux phénomênes ... s'accomplit en même temps dans deux sens opposés». (Теперь г-н Пфаундлер объединил эти два явления в единое понятие, рассматривая наблюдаемый предел как результат двух противоположных реакций, приводя одну в приведенном примере к образованию морской соли [т. е. NaCl] и азотной кислоты, [и] другую к соляной кислоте и нитрату натрия. Это соображение, которое подтверждается экспериментом, оправдывает выражение «химическое равновесие», которое используется для характеристики конечного состояния ограниченных реакций. Я бы предложил перевести это выражение следующим символом:
- HCl + NO 3 Na ⇌ NO 3 H + Cl Na.
- ^ Брэди, Джеймс Э. (2004-02-04). Химия: Материя и ее изменения (4-е изд.). Фред Сенезе. ISBN 0-471-21517-1.
- ^ Аткинс, П.; де Паула, Дж.; Фридман, Р. (2014). Физическая химия – Кванты, материя и изменение , 2-е изд., рис. 73.2. Freeman.
- ^ Шульц, Мэри Джейн (1999). «Почему равновесие? Понимание энтропии смешивания». Журнал химического образования . 76 (10): 1391. Bibcode : 1999JChEd..76.1391S. doi : 10.1021/ed076p1391.
- ^ Clugston, Michael J. (1990). «Математическая проверка второго закона термодинамики из энтропии смешения». Journal of Chemical Education . 67 (3): 203. Bibcode : 1990JChEd..67Q.203C. doi : 10.1021/ed067p203.
- ^ Мортимер, Р. Г. Физическая химия , 3-е изд., стр. 305, Academic Press, 2008.
- ^ Дэвис, CW (1962). Ионная ассоциация . Баттервортс.
- ^ ab Grenthe, I.; Wanner, H. "Guidelines for the extrapolation to zero ionic strength" (PDF) . Архивировано из оригинала (PDF) 2008-12-17 . Получено 2007-05-16 .
- ^ Россотти, Ф. Дж. К.; Россотти, Х. (1961). Определение констант устойчивости . McGraw-Hill.
- ^ abc Иглсон, Мэри (1994). "Биохимия (2-е изд.)" . Краткая энциклопедия химии . ISBN 0-89925-457-8.
- ^ Бек, Монтана; Надьпал, И. (1990). Химия комплексных равновесий (2-е изд.). Будапешт: Академия Кайдо.
- ^ "Нобелевская премия по химии 1967 года". NobelPrize.org . Получено 2019-11-02 .
- ^ Эйген, Манфред (11 декабря 1967 г.). «Неизмеримо быстрые реакции» (PDF) . Нобелевская премия . Архивировано (PDF) из оригинала 2022-10-09 . Получено 2 ноября 2019 г.
- ^ «Константы равновесия – Kc».
- ^ abcd Гордон, Сэнфорд; Макбрайд, Бонни Дж. (1994). "Компьютерная программа для расчета сложных химических равновесных составов и приложений" (PDF) . Справочная публикация NASA 1311. NASA. Архивировано из оригинала (PDF) 2006-04-21.
- ^ Смит, В. Р.; Миссен, Р. В. (1991). Анализ равновесия химической реакции: теория и алгоритмы (переизданное издание). Малабар, Флорида: Krieger Publishing.
- ^ «Системы Mathtrek».
- ^ Диаграмма создана с помощью программы HySS
- ^ "Химическое равновесие с приложениями". NASA. Архивировано из оригинала 1 сентября 2000 г. Получено 5 октября 2019 г.
- ^ C. Kittel, H. Kroemer (1980). "9". Тепловая физика (2-е изд.). WH Freeman Company. ISBN 0-7167-1088-9.
Дальнейшее чтение
- Ван Зеггерен, Ф.; Стори, С. Х. (1970). Вычисление химических равновесий . Cambridge University Press.В основном занимается газофазными равновесиями.
- Леггетт, DJ, ред. (1985). Вычислительные методы определения констант формации . Plenum Press.
- Мартелл, А.Е.; Мотекайтис, Р.Дж. (1992). Определение и использование констант устойчивости . Wiley-VCH.






![{\displaystyle K_{\ce {c}}={\frac {[{\ce {S}}]^{\sigma }[{\ce {T}}]^{\tau }}{[{\ce {A}}]^{\alpha }[{\ce {B}}]^{\beta }}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c2ac61ea07e9614e7c3e261d737d856396c1b178)























![{\displaystyle K={\frac {[\mathrm {S} ]^{\sigma }[\mathrm {T} ]^{\tau }...}{[\mathrm {A} ]^{\alpha } [\mathrm {B} ]^{\beta }...}}\times {\frac {{\gamma _{\mathrm {S} }}^{\sigma }{\gamma _{\mathrm {T} }}^{\tau }...}{{\gamma _{\mathrm {A} }}^{\alpha }{\gamma _{\mathrm {B} }}^{\beta }...}}=K_{\mathrm {c} }\Gamma }](https://wikimedia.org/api/rest_v1/media/math/render/svg/160fbc88403a037161d2c9a44d10cd44746215e8)



![{\displaystyle K_{\mathrm {c} }={\frac {\mathrm {[{CH_{3}CO_{2}}^{-}][{H_{3}O}^{+}]} } {\mathrm {[{CH_{3}CO_{2}H}][{H_{2}O}]} }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/53b93bf6dae8354f02ab3e935fca63b9bd4a16c4)
![{\displaystyle K={\frac {\mathrm {[{CH_{3}CO_{2}}^{-}][{H_{3}O}^{+}]} {\mathrm {[{CH_ {3}CO_{2}H}]} }}=K_{\mathrm {c} }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/472d349477dcf83e95cb3c3423e8ba247ff1d23a)
![{\displaystyle K_{\mathrm {w} }=\mathrm {[H^{+}][OH^{-}]} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/02e72380cadad70b38e1a6f42ce8b217618bc11f)
![{\displaystyle K_{\mathrm {c} }={\frac {\mathrm {[CO_{2}]} {\mathrm {[CO]^{2}} }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/df7ff1e7f45707791cfd9dd8e697fe5695e94f60)
![{\displaystyle {\begin{array}{rl}{\ce {H2A <=> HA^- + H+}}:&K_{1}={\frac {{\ce {[HA-][H+]}} }{{\ce {[H2A]}}}}\\{\ce {HA- <=> A^2- + H+}}:&K_{2}={\frac {{\ce {[A^{2-}][H+]}}}{{\ce {[HA-]}}}}\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/964f444d4c5ff73dc96c30e9eca7e742a64c7cbc)
![{\displaystyle \beta _{{\ce {D}}}={\frac {{\ce {[A^{2-}][H^+]^2}}}{{\ce {[H_2A]}}}}=K_{1}K_{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c204101410770f2cc038f6d29c1a7a0da1d363a1)
![{\displaystyle {\begin{array}{ll}{\ce {A^2- + H+ <=> HA-}}:&\beta _{1}={\frac {{\ce {[HA^-]}}}{{\ce {[A^{2-}][H+]}}}}\\{\ce {A^2- + 2H+ <=> H2A}}:&\beta _{2}={\frac {{\ce {[H2A]}}}{{\ce {[A^{2-}][H+]^2}}}}\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/266ddb8f43fb05b0d3a3195274e597a4fd3d6f37)


![{\displaystyle T_{\mathrm {A} }=\mathrm {[A]+[HA]+[H_{2}A]} \,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b4caf4ff0552bd0430f4b305b3b92c05aef15aa2)
![{\displaystyle T_{\mathrm {H} }=\mathrm {[H]+[HA]+2[H_{2}A]-[OH]} \,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/094ecf5d3e87ba5a02d744835486f24086804cfc)
![{\displaystyle T_{\mathrm {A} }=\mathrm {[A]} +\beta _{1}\mathrm {[A][H]} +\beta _{2}\mathrm {[A][ Н]} ^{2}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f6ae376d767bfb698f8d771a8aa374366c647255)
![{\displaystyle T_{\mathrm {H} }=\mathrm {[H]} +\beta _{1}\mathrm {[A][H]} +2\beta _{2}\mathrm {[A] [H]} ^{2}-K_{w}[\mathrm {H} ]^{-1}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/25502da2d24e51d7cb6c53782a5392673c4b0819)
![{\displaystyle T_{\mathrm {A} }=[\mathrm {A} ]+\sum _{i}p_{i}\beta _{i}[\mathrm {A} ]^{p_{i}}[\mathrm {B} ]^{q_{i}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/de4c20306740d1b3f30387f17ac264b500d313b8)
![{\displaystyle T_{\mathrm {B} }=[\mathrm {B} ]+\sum _{i}q_{i}\beta _{i}[\mathrm {A} ]^{p_{i}}[\mathrm {B} ]^{q_{i}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4c9dea321370bf3d5b01364cfed9dbe3c941ce31)











