Динамическое равновесие
Химическое равновесие обратимой реакции

В химии динамическое равновесие существует, когда происходит обратимая реакция . Вещества переходят между реагентами и продуктами с одинаковой скоростью , что означает отсутствие чистого изменения. Реагенты и продукты образуются с такой скоростью, что концентрация ни того, ни другого не меняется. Это частный пример системы в устойчивом состоянии .

В физике , касающейся термодинамики , закрытая система находится в термодинамическом равновесии , когда реакции происходят с такими скоростями, что состав смеси не меняется со временем. Реакции действительно происходят, иногда бурно, но в такой степени, что изменения в составе не могут быть замечены. Константы равновесия могут быть выражены через константы скорости для обратимых реакций.

Примеры

В новой бутылке газировки концентрация углекислого газа в жидкой фазе имеет определенное значение. Если вылить половину жидкости и закрыть бутылку, углекислый газ будет покидать жидкую фазу с постоянно уменьшающейся скоростью, а парциальное давление углекислого газа в газовой фазе будет увеличиваться до тех пор, пока не будет достигнуто равновесие. В этот момент из-за теплового движения молекула CO 2 может покинуть жидкую фазу, но в течение очень короткого времени другая молекула CO 2 перейдет из газа в жидкость, и наоборот. В равновесии скорость перехода CO 2 из газа в жидкую фазу равна скорости из жидкости в газ. В этом случае равновесная концентрация CO 2 в жидкости определяется законом Генри , который гласит, что растворимость газа в жидкости прямо пропорциональна парциальному давлению этого газа над жидкостью. [1] Это соотношение записывается как

с = К П {\displaystyle c=КП}

где K — константа, зависящая от температуры, P — парциальное давление, а c — концентрация растворенного газа в жидкости. Таким образом, парциальное давление CO 2 в газе увеличивается до тех пор, пока не будет соблюдаться закон Генри. Концентрация углекислого газа в жидкости уменьшается, и напиток теряет часть своей шипучести.

Закон Генри может быть получен путем установления химических потенциалов углекислого газа в двух фазах равными друг другу. Равенство химических потенциалов определяет химическое равновесие . Другие константы для динамического равновесия, включающие фазовые переходы, включают коэффициент распределения и произведение растворимости . Закон Рауля определяет равновесное давление пара идеального раствора

Динамическое равновесие может существовать и в однофазной системе. Простой пример — кислотно-щелочное равновесие, такое как диссоциация уксусной кислоты в водном растворе.

Ч. 3 КООН ↽ − − ⇀ Ч. 3 Операционный директор − + ЧАС + {\displaystyle {\ce {CH3COOH <=> CH3COO- + H+}}}

В состоянии равновесия коэффициент концентрации , K , константа диссоциации кислоты , постоянна (при соблюдении некоторых условий)

К с = [ С ЧАС 3 С О 2 − ] [ ЧАС + ] [ С ЧАС 3 С О 2 ЧАС ] {\displaystyle K_{c}=\mathrm {\frac {[CH_{3}CO_{2}^{-}][H^{+}]}{[CH_{3}CO_{2}H]}} }

В этом случае прямая реакция включает в себя освобождение некоторых протонов из молекул уксусной кислоты, а обратная реакция включает в себя образование молекул уксусной кислоты, когда ион ацетата принимает протон. Равновесие достигается, когда сумма химических потенциалов видов в левой части выражения равновесия равна сумме химических потенциалов видов в правой части. В то же время скорости прямой и обратной реакции равны друг другу. Равновесия, включающие образование химических комплексов, также являются динамическими равновесиями, а концентрации регулируются константами устойчивости комплексов .

Динамические равновесия могут возникать и в газовой фазе, например, при димеризации диоксида азота .

2 НЕТ 2 ↽ − − ⇀ Н 2 О 4 {\displaystyle {\ce {2NO2 <=> N2O4}}} ; К п = [ Н 2 О 4 ] [ Н О 2 ] 2 {\displaystyle K_{p}=\mathrm {\frac {[N_{2}O_{4}]}{[NO_{2}]^{2}}} }

В газовой фазе квадратные скобки указывают парциальное давление. Альтернативно, парциальное давление вещества может быть записано как P(substance). [2]

Связь между равновесием и константами скорости

В простой реакции, такой как изомеризация :

А ↽ − − ⇀ Б {\displaystyle {\ce {A <=> B}}}

необходимо рассмотреть две реакции: прямую реакцию, в которой вещество A превращается в вещество B, и обратную реакцию, в которой вещество B превращается в вещество A. Если обе реакции являются элементарными реакциями , то скорость реакции определяется по формуле [3]

г [ А ] г т = − к ф [ А ] т + к б [ Б ] т {\displaystyle {\frac {d[{\ce {A}}]}{dt}}=-k_{f}[{\ce {A}}]_{t}+k_{b}[{\ce {B}}]_{t}}

где k f — константа скорости прямой реакции, а k b — константа скорости обратной реакции, а квадратные скобки, […] , обозначают концентрацию . Если в начале, в момент времени t = 0 , присутствует только A с концентрацией [A] 0 , сумма двух концентраций, [A] t и [B] t , в момент времени t будет равна [A] 0 .

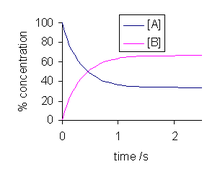
г [ А ] г т = − к ф [ А ] т + к б ( [ А ] 0 − [ А ] т ) {\displaystyle {\frac {d[{\ce {A}}]}{dt}}=-k_{f}[{\ce {A}}]_{t}+k_{b}\left([{\ce {A}}]_{0}-[{\ce {A}}]_{t}\right)}
% концентрации видов в реакции изомеризации. k f = 2 с −1 , k r = 1 с −1

Решение этого дифференциального уравнения:

[ А ] т = к б + к ф е − ( к ф + к б ) т к ф + к б [ А ] 0 {\displaystyle [{\ce {A}}]_{t}={\frac {k_{b}+k_{f}e^{-\left(k_{f}+k_{b}\right)t}}{k_{f}+k_{b}}}[{\ce {A}}]_{0}}

и показано справа. По мере того, как время стремится к бесконечности, концентрации [A] t и [B] t стремятся к постоянным значениям. Пусть t стремится к бесконечности, то есть t → ∞ , в выражении выше:

[ А ] ∞ = к б к ф + к б [ А ] 0 [ Б ] ∞ = к ф к ф + к б [ А ] 0 {\displaystyle [{\ce {A}}]_{\infty }={\frac {k_{b}}{k_{f}+k_{b}}}[{\ce {A}}]_{ 0}\qquad [{\ce {B}}]_{\infty }={\frac {k_{f}}{k_{f}+k_{b}}}[{\ce {A}}]_ {0}}

На практике изменения концентрации не будут измеряться после Поскольку концентрации не меняются после этого, они, по определению , являются равновесными концентрациями. Теперь константа равновесия для реакции определяется как т ⪆ 10 к ф + к б . {\textstyle t\gtrapprox {\frac {10}{k_{f}+k_{b}}}.}

К = [ Б ] экв [ А ] экв {\displaystyle K={\frac {[{\ce {B}}]_{\text{eq}}}{[{\ce {A}}]_{\text{eq}}}}}

Отсюда следует, что константа равновесия численно равна частному констант скорости.

К = к ф к ф + к б [ А ] 0 к б к ф + к б [ А ] 0 = к ф к б {\displaystyle K={\frac {{\frac {k_{f}}{k_{f}+k_{b}}}[{\ce {A}}]_{0}}{{\frac {k_{b}}{k_{f}+k_{b}}}[{\ce {A}}]_{0}}}={\frac {k_{f}}{k_{b}}}}

В общем случае может быть более одной прямой реакции и более одной обратной реакции. Аткинс утверждает [3] , что для общей реакции общая константа равновесия связана с константами скорости элементарных реакций соотношением

К = ( к ф к б ) 1 × ( к ф к б ) 2 × ⋯ {\displaystyle K=\left({\frac {k_{f}}{k_{b}}}\right)_{1}\times \left({\frac {k_{f}}{k_{b}}}\right)_{2}\times \cdots }

Смотрите также

Ссылки

Аткинс, П. В.; де Паула, Дж. (2006). Физическая химия (8-е изд.). Oxford University Press. ISBN 0-19-870072-5.

  1. ^ Аткинс, Раздел 5.3
  2. ^ Денбей, К (1981). Принципы химического равновесия (4-е изд.). Кембридж, Великобритания: Cambridge University Press. ISBN 0-521-28150-4.
  3. ^ ab Аткинс, Раздел 22.4
  • Пример динамического равновесия - проект демонстраций Wolfram
Взято с "https://en.wikipedia.org/w/index.php?title=Динамическое_равновесие&oldid=1249190709"