Вектор (математика и физика)
Элемент векторного пространства

В математике и физике вектор — это термин, который относится к величинам , которые не могут быть выражены одним числом ( скаляром ), или к элементам некоторых векторных пространств . Они должны быть выражены как величиной, так и направлением.

Исторически векторы были введены в геометрии и физике (обычно в механике ) для величин, имеющих как величину, так и направление, таких как перемещения , силы и скорости . Такие величины представлены геометрическими векторами так же, как расстояния , массы и время представлены действительными числами .

Термин вектор также используется в некоторых контекстах для кортежей , которые представляют собой конечные последовательности (чисел или других объектов) фиксированной длины.

Как геометрические векторы, так и кортежи можно складывать и масштабировать, и эти векторные операции привели к концепции векторного пространства, которое представляет собой множество, снабженное векторным сложением и скалярным умножением , которые удовлетворяют некоторым аксиомам, обобщающим основные свойства операций над указанными выше видами векторов. Векторные пространства, образованные геометрическими векторами, называются евклидовыми векторными пространствами , а векторные пространства, образованные кортежами, называются координатными векторными пространствами .

В математике рассматриваются многие векторные пространства, такие как поля расширения , полиномиальные кольца , алгебры и функциональные пространства . Термин вектор обычно не используется для элементов этих векторных пространств и обычно зарезервирован для геометрических векторов, кортежей и элементов неопределенных векторных пространств (например, при обсуждении общих свойств векторных пространств).

Векторы в евклидовой геометрии

Вектор, направленный от А к В

В математике , физике и технике евклидов вектор или просто вектор (иногда называемый геометрическим вектором [1] или пространственным вектором [2] ) — это геометрический объект, имеющий величину (или длину ) и направление . Евклидовы векторы можно складывать и масштабировать для формирования векторного пространства . Векторная величина — это векторнозначная физическая величина , включающая единицы измерения и, возможно, опору , сформулированная как направленный отрезок прямой . Вектор часто изображается графически в виде стрелки, соединяющей начальную точку A с конечной точкой B [3] и обозначается А Б ⟶ . {\textstyle {\stackrel {\longrightarrow }{AB}}.}

Вектор — это то, что нужно для «переноса» точки A в точку B ; латинское слово vector означает «носитель». [4] Впервые он был использован астрономами 18 века, исследовавшими вращение планет вокруг Солнца. [5] Величина вектора — это расстояние между двумя точками, а направление относится к направлению смещения от A к B. Многие алгебраические операции над действительными числами, такие как сложение , вычитание , умножение и отрицание , имеют близкие аналоги для векторов, [6] операций, которые подчиняются знакомым алгебраическим законам коммутативности , ассоциативности и дистрибутивности . Эти операции и связанные с ними законы квалифицируют евклидовы векторы как пример более обобщенной концепции векторов, определяемых просто как элементы векторного пространства .

Векторы играют важную роль в физике : скорость и ускорение движущегося объекта, а также силы, действующие на него, можно описать с помощью векторов. [7] Многие другие физические величины можно с пользой рассматривать как векторы. Хотя большинство из них не представляют расстояния (за исключением, например, положения или смещения ), их величина и направление все равно могут быть представлены длиной и направлением стрелки. Математическое представление физического вектора зависит от системы координат , используемой для его описания. Другие вектороподобные объекты, которые описывают физические величины и преобразуются аналогичным образом при изменении системы координат, включают псевдовекторы и тензоры . [8]

Векторные величины

В естественных науках векторная величина (также известная как векторная физическая величина, физический вектор или просто вектор) — это векторная физическая величина . [9] [10] Обычно она формулируется как произведение единицы измерения и векторного числового значения ( безразмерного ), часто евклидова вектора с величиной и направлением . Например, вектор положения в физическом пространстве может быть выражен тремя декартовыми координатами с единицей СИ — метрами .

В физике и технике , особенно в механике , физический вектор может быть наделен дополнительной структурой по сравнению с геометрическим вектором. [11] Связанный вектор определяется как комбинация обычной векторной величины и точки приложения или точки действия . [9] [12] Связанные векторные величины формулируются как направленный отрезок прямой с определенной начальной точкой помимо величины и направления основного вектора. [9] [11] Например, сила на евклидовой плоскости имеет две декартовы компоненты в единицах СИ ньютонах и сопутствующий двумерный вектор положения в метрах, всего четыре числа на плоскости (и шесть в пространстве). [13] [14] [12] Более простым примером связанного вектора является вектор переноса из начальной точки в конечную точку; в этом случае связанный вектор представляет собой упорядоченную пару точек в одном и том же пространстве положений, причем все координаты имеют одинаковую размерность и единицу измерения (длину и метры). [15] [16] Скользящий вектор — это комбинация обычной векторной величины и линии приложения или линии действия , по которой векторная величина может быть перемещена (без поворотов). Свободный вектор — это векторная величина, имеющая неопределенную опору или область приложения; ее можно свободно перемещать без последствий; вектор смещения — это прототипический пример свободного вектора.

Помимо понятия единиц и поддержки, физические векторные величины могут также отличаться от евклидовых векторов с точки зрения метрики . Например, событие в пространстве-времени может быть представлено как позиционный четырехвектор с когерентной производной единицей метров: оно включает позиционный евклидов вектор и временной компонент, t  ⋅  c 0 (включая скорость света ). В этом случае вместо евклидовой метрики принимается метрика Минковского .

Векторные величины являются обобщением скалярных величин и могут быть далее обобщены как тензорные величины . [16] Отдельные векторы могут быть упорядочены в последовательности во времени ( временной ряд ), например, векторы положения, дискретизирующие траекторию . Вектор может также быть результатом оценки в определенный момент непрерывной векторной функции (например, уравнения маятника ). В естественных науках термин «векторная величина» также охватывает векторные поля, определенные в двух- или трехмерной области пространства, например, скорость ветра над поверхностью Земли.

В качестве физических векторных величин допускаются также псевдовекторы и бивекторы .

Векторные пространства

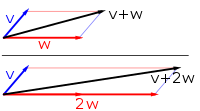
Сложение векторов и скалярное умножение: вектор v (синий) добавляется к другому вектору w (красный, верхняя иллюстрация). Ниже w растягивается в 2 раза, что дает сумму v + 2w .

В математике и физике векторное пространство (также называемое линейным пространством) — это множество , элементы которого, часто называемые векторами , можно складывать и умножать («масштабировать») на числа, называемые скалярами . Операции сложения векторов и умножения скаляров должны удовлетворять определенным требованиям, называемым аксиомами вектора . Действительные векторные пространства и комплексные векторные пространства — это виды векторных пространств, основанные на различных видах скаляров: действительных числах и комплексных числах . Скаляры также могут быть, в более общем смысле, элементами любого поля .

Векторные пространства обобщают евклидовы векторы , которые позволяют моделировать физические величины (такие как силы и скорости ), которые имеют не только величину , но и направление . Концепция векторных пространств является фундаментальной для линейной алгебры , вместе с концепцией матриц , которая позволяет производить вычисления в векторных пространствах. Это обеспечивает краткий и синтетический способ манипулирования и изучения систем линейных уравнений .

Векторные пространства характеризуются своей размерностью , которая, грубо говоря, определяет число независимых направлений в пространстве. Это означает, что для двух векторных пространств над заданным полем и с одинаковой размерностью свойства, зависящие только от структуры векторного пространства, в точности одинаковы (технически векторные пространства изоморфны ) . Векторные пространства являются конечномерными, если их размерность является натуральным числом . В противном случае они являются бесконечномерными , а их размерность является бесконечным кардиналом . Конечномерные векторные пространства естественным образом встречаются в геометрии и смежных областях. Бесконечномерные векторные пространства встречаются во многих областях математики. Например, полиномиальные кольца являются счетно -бесконечномерными векторными пространствами, а многие функциональные пространства имеют мощность континуума в качестве размерности.

Многие векторные пространства, рассматриваемые в математике, также наделены другими структурами . Это случай алгебр , которые включают расширения полей , кольца полиномов, ассоциативные алгебры и алгебры Ли . Это также случай топологических векторных пространств , которые включают функциональные пространства, пространства скалярного произведения , нормированные пространства , гильбертовы пространства и банаховы пространства .

Векторы в алгебре

Каждая алгебра над полем является векторным пространством, но элементы алгебры обычно не называются векторами. Однако в некоторых случаях их называют векторами , в основном по историческим причинам.

Данные представлены векторами

Набор кортежей из n действительных чисел имеет естественную структуру векторного пространства, определяемую покомпонентным сложением и скалярным умножением . Обычно эти кортежи называют векторами , даже в контекстах, где операции векторного пространства не применяются. В более общем смысле, когда некоторые данные могут быть естественным образом представлены векторами, их часто называют векторами, даже когда сложение и скалярное умножение векторов не являются допустимыми операциями для этих данных. [ оспаривается – обсудить ] Вот несколько примеров. Р н {\displaystyle \mathbb {R} ^{n}}

Векторы в исчислении

Исчисление служит основополагающим математическим инструментом в области векторов, предлагая структуру для анализа и манипулирования векторными величинами в различных научных дисциплинах, в частности, физике и инженерии . Векторнозначные функции, где выход является вектором, тщательно изучаются с помощью исчисления для получения существенной информации о движении в трехмерном пространстве. Вектор исчисления расширяет традиционные принципы исчисления на векторные поля, вводя такие операции, как градиент , дивергенция и ротор , которые находят применение в физических и инженерных контекстах. Линейные интегралы , имеющие решающее значение для вычисления работы вдоль пути в силовых полях, и поверхностные интегралы , используемые для определения величин, таких как поток , иллюстрируют практическую полезность исчисления в векторном анализе. Объемные интегралы , имеющие важное значение для вычислений, включающих скалярные или векторные поля в трехмерных областях, способствуют пониманию распределения массы , плотности заряда и скоростей потока жидкости. [ требуется ссылка ]

Смотрите также

Найдите вектор в Викисловаре, бесплатном словаре.

Векторные пространства с большей структурой

Векторные поля

Векторным полем называется векторнозначная функция , которая, как правило, имеет область определения той же размерности (как многообразие ), что и ее область определения,

Смотрите также

  • исчисление Риччи
  • Векторный анализ , учебник по векторному исчислению Уилсона , впервые опубликованный в 1901 году, который внес большой вклад в стандартизацию обозначений и словаря трехмерной линейной алгебры и векторного исчисления.
  • Векторные расслоения — топологическая конструкция, уточняющая идею семейства векторных пространств, параметризованных другим пространством.
  • Вектор исчисления — раздел математики, занимающийся дифференцированием и интегрированием векторных полей.
  • Векторный дифференциал , или del , векторный дифференциальный оператор, представленный символом набла ∇ {\displaystyle \набла}
  • Векторный лапласиан , векторный оператор Лапласа, обозначаемый как , является дифференциальным оператором, определенным над векторным полем ∇ 2 {\displaystyle \набла ^{2}}
  • Векторная нотация , общепринятая нотация, используемая при работе с векторами.
  • Векторный оператор — тип дифференциального оператора, используемый в векторном исчислении.
  • Вектор произведения , или перекрестное произведение, операция над двумя векторами в трехмерном евклидовом пространстве, в результате которой получается третий трехмерный евклидов вектор, перпендикулярный исходным двум.
  • Векторная проекция , также известная как векторная резольюта или векторный компонент , линейное отображение, создающее вектор, параллельный второму вектору.
  • Векторная функция — функция, которая имеет векторное пространство в качестве области значений.
  • Векторизация (математика) , линейное преобразование, преобразующее матрицу в вектор-столбец.
  • Векторная авторегрессия — эконометрическая модель, используемая для отражения эволюции и взаимозависимостей между несколькими временными рядами.
  • Векторный бозон , бозон со спиновым квантовым числом, равным 1
  • Векторная мера — функция, определенная на семействе множеств и принимающая векторные значения, удовлетворяющие определенным свойствам.
  • Векторный мезон , мезон с полным спином 1 и нечетной четностью
  • Векторная квантизация — метод квантования, используемый при обработке сигналов.
  • Векторный солитон , одиночная волна с несколькими компонентами, связанными вместе, которая сохраняет свою форму во время распространения.
  • Векторный синтез , тип аудиосинтеза
  • Фазовый вектор

Примечания

  1. ^ Иванов 2001
  2. ^ Хайнбокель 2001
  3. ^ Ито 1993, с. 1678 г.; Педо 1988 г.
  4. ^ Латинское: vectus, совершенное причастие от vehere, «нести»/ veho = «я несу». Для исторического развития слова vector см. «vector n» . Oxford English Dictionary (Online ed.). Oxford University Press . (Требуется подписка или членство в участвующем учреждении.) и Джефф Миллер. "Самые ранние известные применения некоторых слов математики" . Получено 25.05.2007 .
  5. ↑ Оксфордский словарь английского языка (2-е изд.). Лондон: Clarendon Press. 2001. ISBN 9780195219425.
  6. ^ "вектор | Определение и факты". Encyclopedia Britannica . Получено 2020-08-19 .
  7. ^ "Векторы". www.mathsisfun.com . Получено 2020-08-19 .
  8. ^ Weisstein, Eric W. "Vector". mathworld.wolfram.com . Получено 19 августа 2020 г.
  9. ^ abc "Подробности для номера IEV 102-03-21: "векторная величина"". Международный электротехнический словарь (на японском языке) . Получено 2024-09-07 .
  10. ^ "Подробности для номера IEV 102-03-04: "вектор"". Международный электротехнический словарь (на японском языке) . Получено 2024-09-07 .
  11. ^ ab Rao, A. (2006). Динамика частиц и твердых тел: систематический подход. Cambridge University Press. стр. 3. ISBN 978-0-521-85811-3. Получено 2024-09-08 .
  12. ^ ab Teodorescu, Petre P. (2007-06-06). Механические системы, классические модели: Том 1: Механика частиц. Springer Science & Business Media. ISBN 978-1-4020-5442-6.
  13. ^ Мерчес, И.; Раду, Д. (2014). Аналитическая механика: решения проблем классической физики. CRC Press. стр. 379. ISBN 978-1-4822-3940-9. Получено 2024-09-09 .
  14. ^ Борисенко, А.И.; Тарапов, И.Е.; Сильверман, РА (2012). Векторный и тензорный анализ с приложениями. Dover Books on Mathematics. Dover Publications. стр. 2. ISBN 978-0-486-13190-0. Получено 2024-09-08 .
  15. ^ "Приложение A. Линейная алгебра с геометрической точки зрения". Дифференциальная геометрия: геометрическое введение . Итака, Нью-Йорк: Дэвид В. Хендерсон. 2013. стр.  121– 138. doi :10.3792/euclid/9781429799843-13. ISBN 978-1-4297-9984-3.
  16. ^ ab "ISO 80000-2:2019 - Величины и единицы - Часть 2: Математика". ISO . 2013-08-20 . Получено 2024-09-08 .

Ссылки

Взято с "https://en.wikipedia.org/w/index.php?title=Vector_(mathematics_and_physics)&oldid=1253030865"