Группа комплексного отражения

Понятие в математике

В математике группа комплексных отражений — это конечная группа, действующая в конечномерном комплексном векторном пространстве , которое порождается комплексными отражениями : нетривиальными элементами, которые поточечно фиксируют комплексную гиперплоскость .

Группы комплексных отражений возникают при изучении инвариантной теории многочленных колец . В середине 20-го века они были полностью классифицированы в работах Шепарда и Тодда. Особые случаи включают симметрическую группу перестановок, диэдральные группы и, в более общем смысле, все конечные действительные группы отражений ( группы Кокстера или группы Вейля , включая группы симметрии правильных многогранников ).

Определение

(Комплексное) отражение r (иногда также называемое псевдоотражением или унитарным отражением ) конечномерного комплексного векторного пространства V — это элемент конечного порядка, который фиксирует комплексную гиперплоскость поточечно, то есть фиксированное пространство имеет коразмерность 1. $r\in GL(V)$ $\operatorname {Исправить} (r):=\operatorname {ker} (r-\operatorname {Id} _{V})$

( Конечная ) комплексная группа отражений — это конечная подгруппа, которая порождается отражениями. $W\subseteq GL (V)$ $GL(V)$

Характеристики

Любая действительная группа отражений становится комплексной группой отражений, если мы расширим скаляры от R до C. В частности, все конечные группы Кокстера или группы Вейля дают примеры комплексных групп отражений.

Группа комплексных отражений W неприводима , если единственным W -инвариантным собственным подпространством соответствующего векторного пространства является начало координат. В этом случае размерность векторного пространства называется рангом W .

Число Кокстера неприводимой комплексной группы отражений W ранга определяется как , где обозначает множество отражений, а обозначает множество отражающих гиперплоскостей. В случае действительных групп отражений это определение сводится к обычному определению числа Кокстера для конечных систем Кокстера. $ч$ $n$ $h={\frac {|{\mathcal {R}}|+|{\mathcal {A}}|}{n}}$ ${\mathcal {R}}$ ${\mathcal {A}}$

Классификация

Любая комплексная группа отражений является произведением неприводимых комплексных групп отражений, действующих на сумму соответствующих векторных пространств. ^[1] Поэтому достаточно классифицировать неприводимые комплексные группы отражений.

Неприводимые комплексные группы отражений были классифицированы GC Shephard и JA Todd (1954). Они доказали, что каждая неприводимая группа принадлежит бесконечному семейству G ( m , p , n ) в зависимости от 3 положительных целых параметров (с p , делящим m ) или является одним из 34 исключительных случаев, которые они пронумеровали от 4 до 37. ^[2] Группа G ( m , 1, n ) является обобщенной симметрической группой ; эквивалентно, это сплетение симметрической группы Sym( n ) с циклической группой порядка m . Как матричная группа, ее элементы могут быть реализованы как мономиальные матрицы, ненулевые элементы которых являются корнями m- й степени из единицы .

Группа G ( m , p , n ) является подгруппой индекса p группы G ( m , 1, n ). G ( m , p , n ) имеет порядок m ⁿ n !/ p . Как матрицы, она может быть реализована как подмножество, в котором произведение ненулевых элементов является корнем ( m / p )-й степени из единицы (а не просто корнем m -й степени). Алгебраически, G ( m , p , n ) является полупрямым произведением абелевой группы порядка m ⁿ / p на симметрическую группу Sym( n ); элементы абелевой группы имеют вид ( θ ^{a ₁} , θ ^{a ₂} , ..., θ ^{a _n} ), где θ является примитивным корнем m- й степени из единицы и Σ a _i ≡ 0 mod p , а Sym( n ) действует перестановками координат. ^[3]

Группа G ( m , p , n ) действует неприводимо на C ^{n ,} за исключением случаев m = 1, n > 1 (симметричная группа) и G (2, 2, 2) ( четверная группа Клейна ). В этих случаях C ⁿ распадается как сумма неприводимых представлений размерностей 1 и n − 1.

Особые случаиГ(м,п,н)

Группы Коксетера

При m = 2 представление, описанное в предыдущем разделе, состоит из матриц с действительными элементами, и, следовательно, в этих случаях G ( m , p , n ) является конечной группой Кокстера. В частности: ^[4]

G (1, 1, n ) имеет тип A _{n −1} = [3,3,...,3,3] =...; симметрическая группа порядка n !
G (2, 1, n ) имеет тип B _n = [3,3,...,3,4] =...; гипероктаэдрическая группа порядка 2 ⁿ n !
G (2, 2, n ) имеет тип D _n = [3,3,...,3 ^1,1 ] =..., порядок 2 ⁿ n !/2.

Кроме того, когда m = p и n = 2, группа G ( p , p , 2) является диэдральной группой порядка 2 p ; как группа Кокстера, тип I ₂ ( p ) = [ p ] =(и группа Вейля G ₂ при p = 6).

Другие особые случаи и совпадения

Единственные случаи, когда две группы G ( m , p , n ) изоморфны как комплексные группы отражений ^{[ требуется разъяснение ]} , это когда G ( ma , pa , 1) изоморфна G ( mb , pb , 1) для любых положительных целых чисел a , b (и обе изоморфны циклической группе порядка m / p ). Однако есть и другие случаи, когда две такие группы изоморфны как абстрактные группы.

Группы G (3, 3, 2) и G (1, 1, 3) изоморфны симметрической группе Sym(3). Группы G (2, 2, 3) и G (1, 1, 4) изоморфны симметрической группе Sym(4). Как G (2, 1, 2), так и G (4, 4, 2) изоморфны диэдральной группе порядка 8. А группы G (2 p , p , 1) являются циклическими порядка 2, как и G (1, 1, 2).

Список неприводимых комплексных групп отражений

В первых трех строках этого списка есть несколько дубликатов; подробности см. в предыдущем разделе.

ST — число Шепарда–Тодда группы отражения.
Ранг — это размерность комплексного векторного пространства, в котором действует группа.
Структура описывает структуру группы. Символ * обозначает центральное произведение двух групп. Для ранга 2 частное по (циклическому) центру является группой вращений тетраэдра, октаэдра или икосаэдра ( T = Alt(4), O = Sym(4), I = Alt(5), порядков 12, 24, 60), как указано в таблице. Для обозначения 2 ^{1+4 см} . дополнительную специальную группу .
Порядок — это количество элементов группы.
Reflections описывает количество отражений: 2 ⁶ 4 ¹² означает, что имеется 6 отражений 2-го порядка и 12 отражений 4-го порядка.
Степени дают степени фундаментальных инвариантов кольца полиномиальных инвариантов. Например, инварианты группы номер 4 образуют полиномиальное кольцо с 2 образующими степеней 4 и 6.

СТ	Классифицировать	Структура и названия	Имена Коксетера	Заказ	Размышления	Степени	Кодегреи
1	н −1	Симметрическая группа G (1,1, n ) = Sym( n )		н !	2 ^{n ( n − 1)/2}	2, 3, ..., н	0,1,..., n − 2
2	н	G ( m , p , n ) m > 1, n > 1, p \| m ( G (2,2,2) является приводимым)		м ^н н !/ п	2 ^{мин ( п -1)/2} , d ^{п φ( d )} ( d \| м / п , d > 1)	м ,2 м ,..,( n − 1) м ; mn / п	0, m ,..., ( n − 1) m, если p < m ; 0, m ,...,( n − 2) m , ( n − 1) m − n, если p = m
2	2	Г ( п ,1,2) п > 1,	р[4]2 или	2 п ²	2 ^p , d ^{2φ( d )} ( d \| p , d > 1)	п ; 2п	0, п
2	2	Диэдральная группа G ( p , p ,2) p > 2	[ п ] или	2 стр.	2 ^стр.	2, стр.	0, п-2
3	1	Циклическая группа G ( p ,1,1) = Z _p	р [] или	п	д ^{φ( д )} ( д \| р , д > 1)	п	0
4	2	W(L ₂ ), Z ₂ . T	3[3]3 или, ⟨2,3,3⟩	24	3 ⁸	4,6	0,2
5	2	З ₆ . Т	3[4]3 или	72	3 ¹⁶	6,12	0,6
6	2	З ₄ . Т	3[6]2 или	48	2 ⁶ 3 ⁸	4,12	0,8
7	2	З ₁₂ . Т	‹3,3,3› ₂ или ⟨2,3,3⟩ ₆	144	2 ⁶ 3 ¹⁶	12,12	0,12
8	2	З ₄ . О	4[3]4 или	96	2 ⁶ 4 ¹²	8,12	0,4
9	2	З ₈ . О	4[6]2 илиили ⟨2,3,4⟩ ₄	192	2 ¹⁸ 4 ¹²	8,24	0,16
10	2	Я ₁₂ . О	4[4]3 или	288	2 ⁶ 3 ¹⁶ 4 ¹²	12,24	0,12
11	2	Я ₂₄ . О	⟨2,3,4⟩ ₁₂	576	2 ¹⁸ 3 ¹⁶ 4 ¹²	24,24	0,24
12	2	Z2.O = _ГЛ2 ( Ф3 )	⟨2,3,4⟩	48	2 ¹²	6,8	0,10
13	2	З ₄ . О	⟨2,3,4⟩ ₂	96	2 ¹⁸	8,12	0,16
14	2	З ₆ . О	3[8]2 или	144	2 ¹² 3 ¹⁶	6,24	0,18
15	2	Я ₁₂ . О	⟨2,3,4⟩ ₆	288	2 ¹⁸ 3 ¹⁶	12,24	0,24
16	2	Z ₁₀ . Я , ⟨2,3,5⟩ × Z ₅	5[3]5 или	600	5 ⁴⁸	20,30	0,10
17	2	Я _20. Я	5[6]2 или	1200	2 ³⁰ 5 ⁴⁸	20,60	0,40
18	2	Я _30. Я	5[4]3 или	1800	3 ⁴⁰ 5 ⁴⁸	30,60	0,30
19	2	Z ₆₀ . Я	⟨2,3,5⟩ ₃₀	3600	2 ³⁰ 3 ⁴⁰ 5 ⁴⁸	60,60	0,60
20	2	Я _6. Я	3[5]3 или	360	3 ⁴⁰	12,30	0,18
21	2	Я _12. Я	3[10]2 или	720	2 ³⁰ 3 ⁴⁰	12,60	0,48
22	2	Я _4. Я	⟨2,3,5⟩ ₂	240	2 ³⁰	12,20	0,28
23	3	W(H ₃ ) = Z ₂ × ПСЛ ₂ (5)	[5,3],	120	2 ¹⁵	2,6,10	0,4,8
24	3	W(J ₃ (4)) = Z ₂ × PSL ₂ (7), Клейн	[1 1 1 ⁴ ] ⁴ ,	336	2 ²¹	4,6,14	0,8,10
25	3	W(L ₃ ) = W(P ₃ ) = 3 ¹⁺² .SL ₂ (3) Гессиан	3[3]3[3]3,	648	3 ²⁴	6,9,12	0,3,6
26	3	W(M ₃ ) = Z ₂ ×3 ¹⁺² .SL ₂ (3) Гессиан	2[4]3[3]3,	1296	2 ⁹ 3 ²⁴	6,12,18	0,6,12
27	3	W(J ₃ (5)) = Z ₂ ×( Z ₃ .Alt(6)), Валентинер	[1 1 1 ⁵ ] ⁴ , [1 1 1 ⁴ ] ⁵ ,	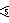2160	2 ⁴⁵	6,12,30	0,18,24
28	4	W(F ₄ ) = (SL ₂ (3)* SL ₂ (3)).( Z ₂ × Z ₂ )	[3,4,3],	1152	2 ¹²⁺¹²	2,6,8,12	0,4,6,10
29	4	W(N ₄ ) = ( Z ₄ *2 ^{1 + 4} ).Симв(5)	[1 1 2] ⁴ ,	7680	2 ⁴⁰	4,8,12,20	0,8,12,16
30	4	W(H ₄ ) = (SL ₂ (5)*SL ₂ (5)). Z ₂	[5,3,3],	14400	2 ⁶⁰	2,12,20,30	0,10,18,28
31	4	W(EN ₄ ) = W(O ₄ ) = ( Z ₄ *2 ^{1 + 4} ).Sp ₄ (2)		46080	2 ⁶⁰	8,12,20,24	0,12,16,28
32	4	W(L ₄ ) = Z ₃ × Sp ₄ (3)	3[3]3[3]3[3]3,	155520	3 ⁸⁰	12,18,24,30	0,6,12,18
33	5	W(K ₅ ) = Z ₂ × Ω ₅ (3) = Z ₂ × PSp ₄ (3) = Z ₂ × PSU ₄ (2)	[1 2 2] ³ ,	51840	2 ⁴⁵	4,6,10,12,18	0,6,8,12,14
34	6	W(K ₆ )= Z ₃ .Ω⁻ ₆(3). Z ₂ , группа Митчелла	[1 2 3] ³ ,	39191040	2 ¹²⁶	6,12,18,24,30,42	0,12,18,24,30,36
35	6	W(E ₆ ) = SO ₅ (3) = O⁻ ₆(2) = ПСп ₄ (3). З ₂ = БП ₄ (2). З ₂	[3 ^2,2,1 ],	51840	2 ³⁶	2,5,6,8,9,12	0,3,4,6,7,10
36	7	W(E7 ₎ = Z2 ×Sp6 ₍ 2 ₎	[3 ^3,2,1 ],	2903040	2 ⁶³	2,6,8,10,12,14,18	0,4,6,8,10,12,16
37	8	W(E ₈ )= Z ₂ .O⁺ ₈(2)	[3 ^4,2,1 ],	696729600	2 ¹²⁰	2,8,12,14,18,20,24,30	0,6,10,12,16,18,22,28

Дополнительную информацию, включая диаграммы, презентации и кодовые степени комплексных рефлексивных групп, см. в таблицах в (Мишель Бруэ, Гюнтер Малле и Рафаэль Рукье, 1998).

Степени

Шепард и Тодд доказали, что конечная группа, действующая на комплексном векторном пространстве, является комплексной группой отражений тогда и только тогда, когда ее кольцо инвариантов является кольцом полиномов ( теорема Шевалле–Шепарда–Тодда ). Поскольку это ранг группы отражений, степени генераторов кольца инвариантов называются степенями W и перечислены в столбце выше под заголовком «степени». Они также показали, что многие другие инварианты группы определяются степенями следующим образом: $\ell$ $d_{1}\leq d_{2}\leq \ldots \leq d_{\ell }$

Центр неприводимой группы отражений является циклической группой порядка, равного наибольшему общему делителю степеней.
Порядок комплексной группы отражений является произведением ее степеней.
Число отражений равно сумме степеней за вычетом ранга.
Неприводимая комплексная группа отражений происходит из действительной группы отражений тогда и только тогда, когда она имеет инвариант степени 2.
Степени d _i удовлетворяют формуле $\prod _{i=1}^{\ell }(q+d_{i}-1)=\sum _{w\in W}q^{\dim(V^{w})}.$

Кодегреи

Для ранга группы отражений кодовые степени W можно определить как $\ell$ $d_{1}^{*}\geq d_{2}^{*}\geq \ldots \geq d_{\ell }^{*}$ $\prod _{i=1}^{\ell }(q-d_{i}^{*}-1)=\sum _{w\in W}\det(w)q^{\dim(V^{w})}.$

Для реальной группы отражений кодепени равны степеням минус 2.
Число гиперплоскостей отражения равно сумме кодовых степеней плюс ранг.

Хорошо сформированные комплексные группы отражения

По определению, каждая комплексная группа отражений порождается своими отражениями. Однако набор отражений не является минимальным порождающим набором, и каждая неприводимая комплексная группа отражений ранга $n$ имеет минимальный порождающий набор, состоящий либо из $n$ , либо из $n + 1$ отражений. В первом случае группа называется хорошо порождаемой .

Свойство быть хорошо порожденным эквивалентно условию для всех . Так, например, из классификации можно вывести, что группа $G$ $($ $m$ $,$ $p$ $,$ $n$ $)$ хорошо порождена тогда и только тогда, когда p = 1 или m . $d_{i}+d_{i}^{*}=d_{\ell }$ $1\leq i\leq \ell$

Для неприводимых хорошо порождённых комплексных групп отражений число Кокстера $h,$ определённое выше, равно наибольшей степени, . Приводимая комплексная группа отражений называется хорошо порождённой, если она является произведением неприводимых хорошо порождённых комплексных групп отражений. Каждая конечная вещественная группа отражений является хорошо порождённой. $h=d_{\ell }$

Группы Шепарда

Хорошо сгенерированные комплексные группы отражений включают подмножество, называемое группами Шепарда . Эти группы являются группами симметрии правильных комплексных многогранников . В частности, они включают группы симметрии правильных вещественных многогранников. Группы Шепарда можно охарактеризовать как комплексные группы отражений, которые допускают представление типа Кокстера с линейной диаграммой. То есть, группа Шепарда имеет ассоциированные положительные целые числа $p 1, ..., p n$ и $q 1, ..., q n - 1$ такие, что существует порождающий набор $s 1, ..., s n ,$ удовлетворяющий соотношениям

(s_{i})^{p_{i}}=1

для

i = 1, ..., n

,

s_{i}s_{j}=s_{j}s_{i}

если ,

|ij|>1

и

s_{i}s_{i+1}s_{i}s_{i+1}\cdots =s_{i+1}s_{i}s_{i+1}s_{i}\cdots

где произведения с обеих сторон имеют

q i

членов, для

i = 1, ..., n - 1

.

Эта информация иногда собирается в символе типа Коксетера $p 1 [q 1] p 2 [q 2] ... [q n - 1] p n$ , как показано в таблице выше.

Среди групп бесконечного семейства $G (m, p, n)$ группы Шепарда — это те, в которых $p = 1.$ Существует также 18 исключительных групп Шепарда, из которых три действительные. ^[5]^[6]

Матрицы Картана

Расширенная матрица Картана определяет унитарную группу. Группы Шепарда ранга n имеют n генераторов. Обычные матрицы Картана имеют диагональные элементы 2, тогда как унитарные отражения не имеют этого ограничения. ^[7] Например, группа ранга 1 порядка p (с символами p[],) определяется матрицей 1 $\times 1$ . $\left[1-e^{2\pi i/p}\right]$

Данный: . $\zeta _{p}=e^{2\pi i/p},\omega =\zeta _{3}=e^{2\pi i/3}={\tfrac {1}{2 }}(-1+i{\sqrt {3}}),\zeta _{4}=e^{2\pi i/4}=i,\zeta _{5}=e^{2\pi i/5}={\tfrac {1}{4}}(\left({\sqrt {5}}-1\right)+i{\sqrt {2(5+{\sqrt {5}})} }),\tau ={\tfrac {1+{\sqrt {5}}}{2}},\lambda ={\tfrac {1+i{\sqrt {7}}}{2}},\omega ={\tfrac {-1+i{\sqrt {3}}}{2}}$

Ранг 1
Группа		Картан	Группа		Картан
2[]		$\left[{\begin{matrix}2\end{matrix}}\right]$	3[]		$\left[{\begin{matrix}1-\omega \end{matrix}}\right]$
4[]		$\left[{\begin{matrix}1-i\end{matrix}}\right]$	5[]		$\left[{\begin{matrix}1-\zeta _{5}\end{matrix}}\right]$

2 место
Группа		Картан	Группа		Картан
Г ₄	3[3]3	$\left[{\begin{smallmatrix}1-\omega &1\\-\omega &1-\omega \end{smallmatrix}}\right]$	Г ₅	3[4]3	$\left[{\begin{smallmatrix}1-\omega &1\\-2\omega &1-\omega \end{smallmatrix}}\right]$
Г ₆	2[6]3	$\left[{\begin{smallmatrix}2&1\\1-\omega +i\omega ^{2}&1-\omega \end{smallmatrix}}\right]$	Г ₈	4[3]4	$\left[{\begin{smallmatrix}1-i&1\\-i&1-i\end{smallmatrix}}\right]$
Г ₉	2[6]4	$\left[{\begin{smallmatrix}2&1\\(1+{\sqrt {2}})\zeta _{8}&1+i\end{smallmatrix}}\right]$	Г ₁₀	3[4]4	$\left[{\begin{smallmatrix}1-\omega &1\\-i-\omega &1-i\end{smallmatrix}}\right]$
Г ₁₄	3[8]2	$\left[{\begin{smallmatrix}1-\omega &1\\1-\omega +\omega ^{2}{\sqrt {2}}&2\end{smallmatrix}}\right]$	Г ₁₆	5[3]5	$\left[{\begin{smallmatrix}1-\zeta _{5}&1\\-\zeta _{5}&1-\zeta _{5}\end{smallmatrix}}\right]$
Г ₁₇	2[6]5	$\left[{\begin{smallmatrix}2&1\\1-\zeta _{5}-i\zeta ^{3}&1-\zeta _{5}\end{smallmatrix}}\right]$	Г ₁₈	3[4]5	$\left[{\begin{smallmatrix}1-\omega &1\\-\omega -\zeta _{5}&1-\zeta _{5}\end{smallmatrix}}\right]$
Г ₂₀	3[5]3	$\left[{\begin{smallmatrix}1-\omega &1\\\omega (\tau -2)&1-\omega \end{smallmatrix}}\right]$	Г ₂₁	2[10]3	$\left[{\begin{smallmatrix}2&1\\1-\omega -i\omega ^{2}\tau &1-\omega \end{smallmatrix}}\right]$

3 место
Группа		Картан	Группа		Картан
Г ₂₂	<5,3,2> ₂	$\left[{\begin{smallmatrix}2&\tau +i-1&-i+1\\-\tau -i-1&2&i\\i-1&-i&2\end{smallmatrix}}\right]$	Г ₂₃	[5,3]	$\left[{\begin{smallmatrix}2&-\tau &0\\-\tau &2&-1\\0&-1&2\end{smallmatrix}}\right]$
Г ₂₄	[1 1 1 ⁴ ] ⁴	$\left[{\begin{smallmatrix}2&-1&-\lambda \\-1&2&-1\\1+\lambda &-1&2\end{smallmatrix}}\right]$	Г ₂₅	3[3]3[3]3	$\left[{\begin{smallmatrix}1-\omega &\omega ^{2}&0\\-\omega ^{2}&1-\omega &-\omega ^{2}\\0&\omega ^{2}&1-\omega \end{smallmatrix}}\right]$
Г ₂₆	3[3]3[4]2	$\left[{\begin{smallmatrix}1-\omega &-\omega ^{2}&0\\\omega ^{2}&1-\omega &-1\\0&-1+\omega &2\end{smallmatrix}}\right]$	Г ₂₇	[1 1 1 ⁵ ] ⁴	$\left[{\begin{smallmatrix}2&-\tau &-\omega \\-\tau &2&-\omega ^{2}\\-\omega ^{2}&\omega &2\end{smallmatrix}}\right]$

4 место
Группа			Картан	Группа			Картан
Г ₂₈	[3,4,3]		$\left[{\begin{smallmatrix}2&-1&0&0\\-1&2&-2&0\\0&-1&2&-1\\0&0&-1&2\end{smallmatrix}}\right]$	Г ₂₉	[1 1 2] ⁴		$\left[{\begin{smallmatrix}2&-1&i+1&0\\-1&2&-i&0\\-i+1&i&2&-1\\0&0&-1&2\end{smallmatrix}}\right]$
Г ₃₀	[5,3,3]		$\left[{\begin{smallmatrix}2&-\tau &0&0\\-\tau &2&-1&0\\0&-1&2&-1\\0&0&-1&2\end{smallmatrix}}\right]$	Г ₃₂	3[3]3[3]3		$\left[{\begin{smallmatrix}1-\omega &\omega ^{2}&0&0\\-\omega ^{2}&1-\omega &-\omega ^{2}&0\\0&\omega ^{2}&1-\omega &\omega ^{2}\\0&0&-\omega ^{2}&1-\omega \end{smallmatrix}}\right]$

5 место
Группа			Картан	Группа			Картан
Г ₃₁	О ₄		$\left[{\begin{smallmatrix}2&-1&i+1&0&-i+1\\-1&2&-i&0&0\\-i+1&i&2&-1&-i+1\\0&0&-1&2&-1\\i+1&0&i+1&-1&2\end{smallmatrix}}\right]$	Г ₃₃	[1 2 2] ³		$\left[{\begin{smallmatrix}2&-1&0&0&0\\-1&2&-1&-1&0\\0&-1&2&-\omega &0\\0&-1&-\omega ^{2}&2&-\omega ^{2}\\0&0&0&-\omega &2\end{smallmatrix}}\right]$

Смотрите также

Параболическая подгруппа группы отражений

Ссылки

^ Лерер и Тейлор, Теорема 1.27.
↑ Лерер и Тейлор, стр. 271.
↑ Лерер и Тейлор, раздел 2.2.
^ Лерер и Тейлор, Пример 2.11.
^ Питер Орлик , Виктор Райнер, Энн В. Шеплер. Знаковое представление для групп Шепарда . Mathematische Annalen . Март 2002, Том 322, Выпуск 3, стр. 477–492. DOI:10.1007/s002080200001 [1]
^ Коксетер, HSM ; Правильные комплексные многогранники , Cambridge University Press, 1974.
^ Унитарные рефлексивные группы, стр.91-93

Broué, Michel ; Malle, Gunter; Rouquier, Raphaël (1995), "О комплексных группах отражений и связанных с ними группах кос" (PDF) , Представления групп (Banff, AB, 1994) , CMS Conf. Proc., т. 16, Providence, RI: American Mathematical Society , стр. 1–13 , MR 1357192
Бруэ, Мишель ; Малле, Гюнтер; Рукье, Рафаэль (1998), «Комплексные группы отражений, группы кос, алгебры Гекке», Journal für die reine und angewandte Mathematik , 1998 (500): 127–190 , CiteSeerX 10.1.1.128.2907 , doi :10.1515/crll.1998.064, ISSN 0075-4102, MR 1637497
Делинь, Пьер (1972), «Les immeubles des groupes de tresses généralisés», Inventiones Mathematicae , 17 (4): 273–302 , Бибкод : 1972InMat..17..273D, doi : 10.1007/BF01406236, ISSN 0020-9910, МР 0422673, S2CID 123680847
Хиллер, Говард Геометрия групп Коксетера. Research Notes in Mathematics, 54. Pitman (Advanced Publishing Program), Бостон, Массачусетс-Лондон, 1982. iv+213 стр. ISBN 0-273-08517-4 *
Лерер, Густав И.; Тейлор, Дональд Э. (2009), Унитарные группы отражения , Серия лекций Австралийского математического общества, т. 20, Cambridge University Press , ISBN 978-0-521-74989-3, г-н 2542964
Шепард, GC; Тодд, JA (1954), "Конечные унитарные группы отражений", Канадский журнал математики , 6 , Канадское математическое общество: 274–304 , doi : 10.4153/CJM-1954-028-3 , ISSN 0008-414X, MR 0059914, S2CID 3342221
Коксетер , Конечные группы, порожденные унитарными отражениями , 1966, 4. Графическая нотация , Таблица n-мерных групп, порожденных n унитарными отражениями. С. 422–423

Внешние ссылки

Страница системы вычислительной алгебры MAGMA

[1] Лерер и Тейлор, Теорема 1.27.

[2] Лерер и Тейлор, стр. 271.

[3] Лерер и Тейлор, раздел 2.2.

[4] Лерер и Тейлор, Пример 2.11.

[5] Питер Орлик , Виктор Райнер, Энн В. Шеплер. Знаковое представление для групп Шепарда . Mathematische Annalen . Март 2002, Том 322, Выпуск 3, стр. 477–492. DOI:10.1007/s002080200001 [1]

[6] Коксетер, HSM ; Правильные комплексные многогранники , Cambridge University Press, 1974.

[7] Унитарные рефлексивные группы, стр.91-93