Евклидовы мозаики выпуклыми правильными многоугольниками
Разбиение плоскости на многоугольники, все из которых правильные
Примеры периодических мозаик

Правильная мозаика имеет один тип правильной грани.
Полуправильная или однородная мозаика имеет один тип вершин , но два или более типов граней.

k-однородная мозаика имеет k типов вершин и два или более типов правильных граней.
Укладка плитки без стыков может иметь правильные грани разного размера.

Разбиение евклидовой плоскости на выпуклые правильные многоугольники широко использовалось со времен античности. Первая систематическая математическая обработка была сделана Кеплером в его Harmonices Mundi ( лат . Гармония мира , 1619).

Обозначение евклидовых мозаик

Евклидовы мозаики обычно называются в честь нотации Канди и Роллетта. [1] Эта нотация представляет (i) количество вершин, (ii) количество многоугольников вокруг каждой вершины (расположенных по часовой стрелке) и (iii) количество сторон каждого из этих многоугольников. Например: 3 6 ; 3 6 ; 3 4 .6, говорит нам, что есть 3 вершины с 2 различными типами вершин, поэтому эта мозаика будет классифицироваться как «3-однородная (2-вершинные типы)» мозаика. Разбитая, 3 6 ; 3 6 (обе разного класса транзитивности), или (3 6 ) 2 , говорит нам, что есть 2 вершины (обозначенные верхним индексом 2), каждая с 6 равносторонними 3-сторонними многоугольниками (треугольниками). С конечной вершиной 3 4 .6, еще 4 смежных равносторонних треугольника и один правильный шестиугольник.

Однако эта нотация имеет две основные проблемы, связанные с неоднозначной конформацией и уникальностью [2] Во-первых, когда дело доходит до k-однородных мозаик, нотация не объясняет отношения между вершинами. Это делает невозможным создание покрытой плоскости, имея только нотацию. И, во-вторых, некоторые мозаики имеют одинаковую номенклатуру, они очень похожи, но можно заметить, что относительное положение шестиугольников различно. Следовательно, вторая проблема заключается в том, что эта номенклатура не является уникальной для каждой мозаики.

Для решения этих проблем нотация Гомджау-Хогга [3] представляет собой слегка измененную версию исследования и нотации, представленных в 2012 году [2] о генерации и номенклатуре тесселяций и двухслойных сеток. Antwerp v3.0 [4] — бесплатное онлайн-приложение, позволяющее бесконечно генерировать правильные многоугольные мозаики с помощью набора этапов размещения фигур и итеративных операций вращения и отражения, полученных непосредственно из нотации Гомджау-Хогга.

Регулярные плитки

Согласно Грюнбауму и Шепарду (раздел 1.3), мозаика называется регулярной , если группа симметрии мозаики действует транзитивно на флаги мозаики, где флаг — это тройка, состоящая из взаимно инцидентной вершины , ребра и плитки мозаики. Это означает, что для каждой пары флагов существует операция симметрии, отображающая первый флаг во второй. Это эквивалентно тому, что мозаика является мозаикой « ребро-к-ребру» из конгруэнтных правильных многоугольников. В вершине должно быть шесть равносторонних треугольников , четыре квадрата или три правильных шестиугольника , что дает три правильных мозаики .

Правильные мозаики (3)
стр6м, *632стр4м, *442

C&R: 3 6
ГДж-H: 3/м30/r(h2)
( t = 1, e = 1)
C&R: 6 3
ГДж-H: 6/м30/r(h1)
( t = 1, e = 1)
C&R: 4 4
GJ-H: 4/m45/r(h1)
( t = 1, e = 1)

C&R: Нотация Канди и Ролле
GJ-H: Нотация Гомджау-Хогга

Архимедовы, равномерные или полуправильные мозаики

Транзитивность вершин означает, что для каждой пары вершин существует операция симметрии, отображающая первую вершину во вторую. [5]

Если требование флаговой транзитивности ослабить до требования вершинной транзитивности, при этом условие, что мозаика является ребро-к-ребру, сохраняется, то возможны восемь дополнительных мозаик, известных как архимедовы , равномерные или полуправильные мозаики. Обратите внимание, что существуют две зеркальные (энантиоморфные или хиральные ) формы мозаики 3 4 .6 (плосконосый шестиугольный), только одна из которых показана в следующей таблице. Все остальные правильные и полуправильные мозаики являются ахиральными.

Равномерные плитки (8)
стр6м, *632



C&R: 3,12 2
ГДж-H: 12-3/м30/r(h3)
( t = 2, e = 2)
t {6,3}


C&R: 3.4.6.4
GJ-H: 6-4-3/m30/r(c2)
( t = 3, e = 2)
rr {3,6}


C&R: 4.6.12
GJ-H: 12-6,4/м30/r(c2)
( t = 3, e = 3)
tr {3,6}


C&R: (3.6) 2
GJ-H: 6-3-6/m30/r(v4)
( t = 2, e = 1)
r {6,3}



C&R: 4.8 2
GJ-H: 8-4/m90/r(h4)
( t = 2, e = 2)
t {4,4}


C&R: 3 2 .4.3.4
GJ-H: 4-3-3,4/r90/r(h2)
( t = 2, e = 2)
s {4,4}


C&R: 3 3 .4 2
GJ-H: 4-3/m90/r(h2)
( t = 2, e = 3)
{3,6}: e


C&R: 3 4 .6
GJ-H: 6-3-3/r60/r(h5)
( t = 3, e = 3)
ср {3,6}

C&R: Нотация Канди и Ролле
GJ-H: Нотация Гомджау-Хогга

Грюнбаум и Шепард различают описание этих мозаик как архимедовых , ссылаясь только на локальное свойство расположения плиток вокруг каждой вершины, которое является одинаковым, и как единообразных , ссылаясь на глобальное свойство транзитивности вершин. Хотя они дают один и тот же набор мозаик на плоскости, в других пространствах есть архимедовы мозаики, которые не являются однородными.

Мозаики с плоскостями и вершинами

Существует 17 комбинаций правильных выпуклых многоугольников, которые образуют 21 тип мозаик с плоской вершиной . [6] [7] Многоугольники в них встречаются в точке без зазора или перекрытия. Перечисляя по их вершинным фигурам , один имеет 6 многоугольников, три имеют 5 многоугольников, семь имеют 4 многоугольника и десять имеют 3 многоугольника. [8]

Три из них могут создавать правильные мозаики (6 3 , 4 4 , 3 6 ), а еще восемь могут создавать полуправильные или архимедовы мозаики (3.12.12, 4.6.12, 4.8.8, (3.6) 2 , 3.4.6.4, 3.3.4.3.4, 3.3.3.4.4, 3.3.3.3.6). Четыре из них могут существовать в более высоких k-однородных мозаиках (3.3.4.12, 3.4.3.12, 3.3.6.6, 3.4.4.6), в то время как шесть из них не могут быть использованы для полного замощения плоскости правильными многоугольниками без зазоров или наложений — они полностью замощают пространство только при включении неправильных многоугольников (3.7.42, 3.8.24, 3.9.18, 3.10.15, 4.5.20, 5.5.10). [9]

Мозаики с плоскостями и вершинами
6
3 6
5
3.3.4.3.4
3.3.3.4.4
3.3.3.3.6
4
3.3.4.12
3.4.3.12
3.3.6.6
(3.6) 2
3.4.4.6
3.4.6.4
4 4
3
3.7.42
3.8.24
3.9.18
3.10.15
3.12.12
4.5.20
4.6.12
4.8.8
5.5.10
6 3

к-равномерная укладка

Такие периодические мозаики можно классифицировать по числу орбит вершин, ребер и плиток. Если имеется k орбит вершин, мозаика известна как k -равномерная или k -изогональная; если имеется t орбит плиток, как t -изоэдральная; если имеется e орбит ребер, как e -изотоксальная.

k -однородные мозаики с одинаковыми вершинными фигурами можно дополнительно идентифицировать по их групповой симметрии.

1-однородные мозаики включают 3 правильные мозаики и 8 полуправильных, с 2 или более типами правильных многоугольных граней. Существует 20 2-однородных мозаик, 61 3-однородная мозаика, 151 4-однородная мозаика, 332 5-однородных мозаики и 673 6-однородных мозаики. Каждая из них может быть сгруппирована по числу m различных вершинных фигур, которые также называются m -архимедовыми мозаиками. [10]

Наконец, если число типов вершин совпадает с однородностью ( m = k ниже), то говорят, что мозаика является Кротенхердтовой . В общем случае однородность больше или равна числу типов вершин ( m ≥ k ), так как разные типы вершин обязательно имеют разные орбиты, но не наоборот. Если положить m = n = k , то получится 11 таких мозаик для n = 1; 20 таких мозаик для n = 2; 39 таких мозаик для n = 3; 33 таких мозаики для n = 4; 15 таких мозаик для n = 5; 10 таких мозаик для n = 6; и 7 таких мозаик для n = 7.

Ниже приведен пример 3-однородной мозаики:

Цветная 3-х кратная мозаика №57 из 61

по сторонам, желтые треугольники, красные квадраты (по многоугольникам)
по 4-х равногранным позициям, 3 закрашенных цвета треугольников (по орбитам)
k -равномерный, m -архимедовы подсчеты мозаики [11] [12] [13]
м -Архимедов
1234567891011121314≥ 15Общий
к -равномерный1110000000000000011
2020000000000000020
30223900000000000061
4033853300000000000151
507414994150000000000332
601002841879210000000000673
70175572426218747000000001472
80298103779553720320000000002850
9042419921608127857080800000005960
100663377229792745146821227000000011866
1101086717157985993371164752100000024459
1201607137621100612309923017361291500000049794
130?????????00000103082
140?????????00000?
≥ 150?????????????0?
Общий11∞∞∞∞∞∞∞∞∞∞∞∞∞0∞

2-однородные мозаики

Существует двадцать (20) 2-однородных мозаик евклидовой плоскости. (также называемых 2- изогональными мозаиками или полуправильными мозаиками ) [5] : 62-67  [14] [15] Типы вершин перечислены для каждой. Если две мозаики имеют одинаковые два типа вершин, им даются индексы 1,2.

2-однородные мозаики (20)
стр6м, *632стр4м, *442

[3 6 ; 3 2 .4.3.4]
3-4-3/m30/r(c3)
( t = 3, e = 3)
[3.4.6.4; 3 2 .4.3.4]
6-4-3,3/м30/r(h1)
( t = 4, e = 4)
[3.4.6.4; 3 3 .4 2 ]
6-4-3-3/м30/р(ч5)
( т = 4, е = 4)
[3.4.6.4; 3,4 2 , 6]
6-4-3,4-6/m30/r(c4)
( t = 5, e = 5)
[4.6.12; 3.4.6.4]
12-4,6-3/м30/р(с3)
( t = 4, e = 4)
[3 6 ; 3 2 .4.12]
12-3,4-3/м30/r(c3)
( t = 4, e = 4)
[3.12.12; 3.4.3.12]
12-0,3,3-0,4/м45/м(h1)
( t = 3, e = 3)
стр6м, *632стр.6, 632стр.6, 632смм, 2*22пмм, *2222смм, 2*22пмм, *2222

[3 6 ; 3 2 .6 2 ]
3-6/м30/r(c2)
( t = 2, e = 3)
[3 6 ; 3 4 .6] 1
6-3,3-3/м30/r(h1)
( t = 3, e = 3)
[3 6 ; 3 4 .6] 2
6-3-3,3-3/r60/r(h8)
( t = 5, e = 7)
[3 2 .6 2 ; 3 4 .6]
6-3/м90/г(h1)
( t = 2, е = 4)
[3.6.3.6; 3 2 .6 2 ]
6-3,6/м90/r(h3)
( t = 2, e = 3)
[3.4 2 .6; 3.6.3.6] 2
6-3,4-6-3,4-6,4/m90/r(c6)
( t = 3, e = 4)
[3.4 2 .6; 3.6.3.6] 1
6-3,4/м90/р(h4)
( t = 4, е = 4)
п4г, 4*2пгг, 22×смм, 2*22смм, 2*22пмм, *2222смм, 2*22

[3 3 .4 2 ; 3 2 .4.3.4] 1
4-3,3-4,3/r90/m(h3)
( t = 4, e = 5)
[3 3 .4 2 ; 3 2 .4.3.4] 2
4-3,3,3-4,3/r(c2)/r(h13)/r(h45)
( t = 3, e = 6)
[4 4 ; 3 3 .4 2 ] 1
4-3/м(h4)/м(h3)/р(h2)
( t = 2, е = 4)
[4 4 ; 3 3 .4 2 ] 2
4-4-3-3/m90/r(h3)
( t = 3, e = 5)
[3 6 ; 3 3 .4 2 ] 1
4-3,4-3,3/m90/r(h3)
( t = 3, e = 4)
[3 6 ; 3 3 .4 2 ] 2
4-3-3-3/м90/р(h7)/р(h5)
( t = 4, e = 5)

Вышек-равномерная укладка

k -однородные мозаики были пронумерованы до 6. Существует 673 6-однородных мозаик евклидовой плоскости. Поиск Брайана Гейлбаха воспроизвел список Кротенхердта из 10 6-однородных мозаик с 6 различными типами вершин, а также нашел 92 из них с 5 типами вершин, 187 из них с 4 типами вершин, 284 из них с 3 типами вершин и 100 с 2 типами вершин.

Фрактализацияк-равномерная укладка

Существует много способов создания новых k -однородных мозаик из старых k -однородных мозаик. Например, обратите внимание, что 2-однородная мозаика [3.12.12; 3.4.3.12] имеет квадратную решетку, 4(3-1)-однородная мозаика [343.12; (3.12 2 )3] имеет плосконосую квадратную решетку, а 5(3-1-1)-однородная мозаика [334.12; 343.12; (3.12.12)3] имеет удлиненную треугольную решетку. Эти однородные мозаики более высокого порядка используют ту же решетку, но обладают большей сложностью. Фрактальная основа для этих мозаик следующая: [16]

ТреугольникКвадратШестиугольникРазрезанный
двенадцатиугольник
Форма
Фрактализация

Длины сторон увеличены в . раз . 2 + 3 {\displaystyle 2+{\sqrt {3}}}

Аналогично это можно сделать, взяв за основу усеченную тригексагональную мозаику, с соответствующим расширением . 3 + 3 {\displaystyle 3+{\sqrt {3}}}

ТреугольникКвадратШестиугольникРазрезанный
двенадцатиугольник
Форма
Фрактализация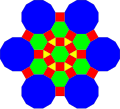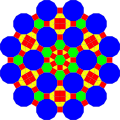

Примеры фрактализации

Усеченная шестиугольная мозаикаУсеченная тригексагональная мозаика
Фрактализация

Плитки, не являющиеся ребром к краю

Выпуклые правильные многоугольники также могут образовывать плоские мозаики, которые не являются ребром к ребру. Такие мозаики можно рассматривать как неправильные многоугольники с соседними коллинеарными ребрами.

Существует семь семейств изогональных фигур , каждое из которых имеет действительный параметр, определяющий перекрытие сторон соседних плиток или соотношение длин сторон разных плиток. Два семейства генерируются из сдвинутых квадратов, либо прогрессивных, либо зигзагообразных положений. Грюнбаум и Шепард называют эти плитки однородными, хотя это противоречит определению Коксетера для однородности, которое требует правильных многоугольников от края до края. [17] Такие изогональные плитки на самом деле топологически идентичны однородным плиткам, с другими геометрическими пропорциями.

Периодические изогональные мозаики из выпуклых правильных многоугольников, не соединенных ребром к ребру
1234567

Ряды квадратов с горизонтальными смещениями
Ряды треугольников с горизонтальными смещениями
Мозаика из квадратов
Три шестиугольника окружают каждый треугольник.
Каждый шестиугольник окружают шесть треугольников.
Треугольники трех размеров
смм (2*22)стр2 (2222)смм (2*22)п4м (*442)стр.6 (632)стр.3 (333)
Шестиугольная мозаикаКвадратная плиткаУсеченная квадратная мозаикаУсеченная шестиугольная мозаикаШестиугольная мозаикаТригексагональная мозаика

Смотрите также

Ссылки

  1. ^ Канди, Х. М.; Роллетт, А. П. (1981). Математические модели; Стрэдброк (Великобритания): Tarquin Publications.
  2. ^ ab Gomez-Jauregui, Valentin al.; Otero, Cesar; et al. (2012). «Создание и номенклатура тесселяций и двухслойных сеток». Журнал структурной инженерии . 138 (7): 843– 852. doi : 10.1061/(ASCE)ST.1943-541X.0000532. hdl : 10902/5869 .
  3. ^ Гомес-Хауреги, Валентин; Хогг, Харрисон; и др. (2021). "Нотация ГомДжау-Хогга для автоматического создания k-однородных мозаик с помощью ANTWERP v3.0". Симметрия . 13 (12): 2376. Bibcode :2021Symm...13.2376G. doi : 10.3390/sym13122376 . hdl : 10902/23907 .
  4. ^ Хогг, Харрисон; Гомес-Хореги, Валентин. < «Антверпен 3.0».
  5. ^ ab Critchlow, K. (1969). Order in Space: A Design Source Book . Лондон: Thames and Hudson. С.  60–61 .
  6. ^ Даллас, Элмсли Уильям (1855), Элементы плоской практической геометрии и т. д., Джон У. Паркер и сын, стр. 134
  7. ^ Мозаики и узоры , Рисунок 2.1.1, стр.60
  8. ^ Мозаика и узоры , стр. 58-69
  9. ^ "Pentagon-Decagon Packing". Американское математическое общество . AMS . Получено 2022-03-07 .
  10. ^ k-однородные мозаики правильными многоугольниками Архивировано 30.06.2015 на Wayback Machine Нильс Леннгрен, 2009
  11. ^ "n-однородные мозаики". probabilitysports.com . Получено 21.06.2019 .
  12. ^ Sloane, N. J. A. (ред.). "Последовательность A068599 (Число n-однородных мозаик.)". Онлайновая энциклопедия целочисленных последовательностей . Фонд OEIS . Получено 07.01.2023 .
  13. ^ "Перечисление n-однородных k-архимедовых мозаик". zenorogue.github.io/tes-catalog/?c= . Получено 2024-08-24 .
  14. ^ Мозаики и узоры , Грюнбаум и Шепард 1986, стр. 65-67
  15. ^ "In Search of Demiregular Tilings" (PDF) . Архивировано из оригинала (PDF) 2016-05-07 . Получено 2015-06-04 .
  16. ^ Чави, Дарра (2014). «МОЗАИРОВКИ ПРАВИЛЬНЫМИ МНОГОУГОЛЬНИКАМИ III: ПЛОТНЫЕ ДОДЕКАГОНАЛЬНЫЕ МОЗАИКИ». Симметрия-Культура и наука . 25 (3): 193– 210. S2CID  33928615.
  17. ^ "Tilings by regular polygons" (PDF) . стр. 236. Архивировано из оригинала (PDF) 2016-03-03.
  • Грюнбаум, Бранко; Шепард, Джеффри К. (1977). «Tilings by regular polygons». Math. Mag . 50 (5): 227– 247. doi :10.2307/2689529. JSTOR  2689529.
  • Грюнбаум, Бранко; Шепард, GC (1978). «Девяносто один тип изогональных мозаик на плоскости». Trans. Am. Math. Soc . 252 : 335– 353. doi : 10.1090/S0002-9947-1978-0496813-3 . MR  0496813.
  • Деброй, И.; Ландуит, Ф. (1981). «Эквитранзитивные реберные мозаики». Геометрии Дедиката . 11 (1): 47–60 . doi : 10.1007/BF00183189. S2CID  122636363.
  • Грюнбаум, Бранко ; Шепард, GC (1987). Tilings and Patterns . WH Freeman and Company. ISBN 0-7167-1193-1.
  • Рен, Динг; Рей, Джон Р. (1987). «Характеристика границы и теорема Пика в архимедовых плоских мозаиках». J. Comb. Theory A. 44 ( 1): 110– 119. doi :10.1016/0097-3165(87)90063-X.
  • Чави, Д. (1989). «Мозаики правильными многоугольниками — II: Каталог мозаик» . Компьютеры и математика с приложениями . 17 : 147– 165. doi :10.1016/0898-1221(89)90156-9.
  • Порядок в пространстве: Справочник по дизайну, Кейт Кричлоу, 1970 ISBN 978-0-670-52830-1 
  • Соммервилл, Дункан Макларен Янг (1958). Введение в геометрию n измерений . Dover Publications.Глава X: Правильные многогранники
  • Преа, П. (1997). «Последовательности расстояний и пороги перколяции в архимедовых мозаиках». Матем. вычисл. моделирование . 26 ( 8– 10): 317– 320. doi :10.1016/S0895-7177(97)00216-1.
  • Кович, Юрий (2011). «Графы типа симметрии платоновых и архимедовых тел». Math. Commun . 16 (2): 491– 507.
  • Пеллисер, Дэниел; Уильямс, Гордон (2012). «Минимальные покрытия архимедовых мозаик, часть 1». Электронный журнал комбинаторики . 19 (3): #P6. doi : 10.37236/2512 .
  • Дейл Сеймур и Джилл Бриттон , Введение в тесселяцию , 1989, ISBN 978-0866514613 , стр. 50–57 

Ссылки на евклидовы и общие мозаики:

Получено с "https://en.wikipedia.org/w/index.php?title=Евклидовы_плитки_выпуклыми_регулярными_полигонами&oldid=1268508825"