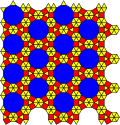
Демирегулярная мозаика

В геометрии полурегулярные мозаики — это набор евклидовых мозаик, сделанных из 2 или более правильных многоугольных граней. Разные авторы перечисляли разные наборы мозаик. Более систематический подход, рассматривающий орбиты симметрии , — это 2-однородные мозаики , которых существует 20. Некоторые из полурегулярных мозаик на самом деле являются 3-однородными мозаиками .

Грюнбаум и Шепард перечислили полный список 20 2-однородных мозаик в книге «Мозаики и узоры» (1987):

2-однородные мозаики

смм, 2*22 (4 4 ; 3 3 .4 2 ) 1	смм, 2*22 (4 4 ; 3 3 .4 2 ) 2	пмм, *2222 (3 6 ; 3 3 .4 2 ) 1	смм, 2*22 (3 6 ; 3 3 .4 2 ) 2	смм, 2*22 (3,4 2 , 6; (3,6) 2 ) 2	пмм, *2222 (3,4 2 , 6; (3,6) 2 ) 1	пмм, *2222 ((3,6) 2 ; 3 2 .6 2 )
стр4м, *442 ( 3.12.12; 3.4.3.12 )	п4г, 4*2 (3 3 .4 2 ; 3 2 .4.3.4) 1	пгг, 2× (3 3 .4 2 ; 3 2 .4.3.4) 2	стр6м, *632 (3 6 ; 3 2 .6 2 )	стр6м, *632 (3 6 ; 3 4 .6) 1	стр.6, 632 (3 6 ; 3 4 .6) 2	смм, 2*22 (3 2 .6 2 ; 3 4 .6)
стр6м, *632 (3 6 ; 3 2 .4.3.4)	стр6м, *632 (3.4.6.4; 3 2 .4.3.4)	стр6м, *632 (3.4.6.4; 3 3 .4 2 )	стр6м, *632 (3.4.6.4; 3.4 2 .6)	стр6м, *632 (4.6.12; 3.4.6.4)	стр6м, *632 (3 6 ; 3 2 .4.12)

Гика перечисляет 10 из них с 2 или 3 типами вершин, называя их полурегулярными полиморфными разбиениями. ^[1]

Пластина XXVII № 12 4.6.12 3.4.6.4	№ 13 3.4.6.4 3.3.3.4.4	№ 13 бис. 3.4.4.6 3.3.4.3.4	№ 13 тер. 3.4.4.6 3.3.3.4.4	Табличка XXIV № 13, кватурор. 3.4.6.4 3.3.4.3.4
№ 14 3 3 .4 2 3 6	Табличка XXVI № 14-бис. 3.3.4.3.4 3.3.3.4.4 3 6	№ 14 тер. 3 3 .4 2 3 6	№ 15 3.3.4.12 3 6	Пластина XXV № 16 3.3.4.12 3.3.4.3.4 3 6

Штейнхауз приводит 5 примеров неоднородных мозаик правильных многоугольников, помимо 11 правильных и полуправильных. ^[2] (Все они имеют 2 типа вершин, а одна из них является 3-однородной.)

2-единообразный				3-единообразный
Изображение 85 3 3 .4 2 3.4.6.4	Изображение 86 3 2 .4.3.4 3.4.6.4	Изображение 87 3.3.4.12 3 6	Изображение 89 3 3 .4 2 3 2 .4.3.4	Изображение 88 3.12.12 3.3.4.12

Кричлоу выделяет 14 полурегулярных мозаик, из которых 7 являются 2-однородными, а 7 — 3-однородными.

Он кодирует буквенные названия типов вершин с верхними индексами для различения порядков граней. Он распознает, что A, B, C, D, F и J не могут быть частью непрерывных покрытий всей плоскости.

А (нет)	Б (нет)	С (нет)	Д (нет)	E (полу)	Ф (нет)	Г (полу)	H (полу)	Дж (нет)	К (2) (рег.)
3.7.42	3.8.24	3.9.18	3.10.15	3.12.12	4.5.20	4.6.12	4.8.8	5.5.10	6 3
L1 (деми)	L2 (деми)	М1 (деми)	М2 (полу)	N1 (деми)	N2 (полу)	П (3) (рег.)	Q1 (полу)	Q2 (полу)	Р (полу)	С (1) (рег.)
3.3.4.12	3.4.3.12	3.3.6.6	3.6.3.6	3.4.4.6	3.4.6.4	4 4	3.3.4.3.4	3.3.3.4.4	3.3.3.3.6	3 6

2-униформы

1	2	4	6	7	10	14
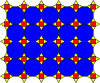( 3.12.12; 3.4.3.12 )	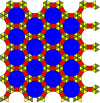(3 6 ; 3 2 .4.12)	(4.6.12; 3.4.6.4)	((3,6) 2 ; 3 2 .6 2 )	(3.4.6.4; 3 2 .4.3.4)	(3 6 ; 3 2 .4.3.4)	(3.4.6.4; 3.4 2 .6)
Э+Л2	Л1+(1)	Н1+Г	М1+М2	Н2+К1	К1+(1)	Н1+К2

3-униформы

3	5	8	9	11	12	13
(3.3.4.3.4; 3.3.4.12, 3.4.3.12)	(3 6 ; 3.3.4.12; 3.3.4.3.4)	(3.3.4.3.4; 3.3.3.4.4, 4.3.4.6)	(3 6 , 3.3.4.3.4)	(3 6 ; 3.3.4.3.4, 3.3.3.4.4)	(3 6 ; 3.3.4.3.4; 3.3.3.4.4)	(3.4.6.4; 3.4 2 .6)
Л1+Л2+К1	Л1+Q1+(1)	Н1+Q1+Q2	К1+(1)	Q1+Q2+(1)	Q1+Q2+(1)	Н1+Н2
Заявленные тайлинги и дуалы

• Гика, М. Геометрия искусства и жизни , (1946), 2-е издание, Нью-Йорк: Довер, 1977.
• Кейт Кричлоу, «Порядок в пространстве: справочник по дизайну» , 1970, стр. 62–67
• Уильямс, Роберт (1979). Геометрическая основа естественной структуры: первоисточник дизайна . Dover Publications, Inc. ISBN 0-486-23729-X.стр. 35–43
• Штейнхаус, Х. Математические снимки, 3-е изд., (1969), Oxford University Press, и (1999) Нью-Йорк: Довер
• Грюнбаум, Бранко ; Шепард, GC (1987). Мозаики и узоры . WH Freeman. ISBN 0-7167-1193-1.стр. 65
• Чави, Д. (1989). «Мозаики правильными многоугольниками — II: Каталог мозаик». Компьютеры и математика с приложениями . 17 : 147–165. doi :10.1016/0898-1221(89)90156-9.
• В поисках полурегулярных мозаик, Хелмер Аслаксен

• Вайсштейн, Эрик В. «Демирегулярная мозаика». MathWorld .
• n-однородные мозаики Брайан Галебах