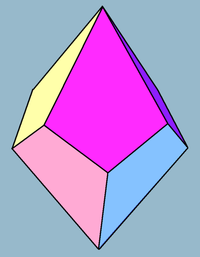
Тетрагональный трапецоэдр
| Тетрагональный трапецоэдр | |
|---|---|
 Нажмите на картинку для увеличения. | |
| Тип | трапецоэдры |
| Конвей | дА4 |
| Диаграмма Коксетера |           |
| Лица | 8 воздушных змеев |
| Края | 16 |
| Вершины | 10 |
| Конфигурация лица | В4.3.3.3 |
| Группа симметрии | Д 4д , [2 + ,8], (2*4), порядок 16 |
| Группа вращения | D 4 , [2,4] + , (224), порядок 8 |
| Двойной многогранник | Квадратная антипризма |
| Характеристики | выпуклый, гранепереходный |
В геометрии тетрагональный трапецоэдр , или дельтоэдр , является вторым в бесконечном ряду трапецоэдров , которые двойственны антипризмам . Он имеет восемь граней, которые являются конгруэнтными кайтами , и двойственен квадратной антипризме .
В генерации сетки
Эта форма использовалась в качестве тестового случая для генерации гексаэдрической сетки , [1] [2] [3] [4] [5] упрощая более ранний тестовый случай, предложенный математиком Робертом Шнайдерсом в виде квадратной пирамиды с границей, разделенной на 16 четырехугольников. В этом контексте тетрагональный трапецоэдр также назывался кубическим октаэдром , [3] четырехсторонним октаэдром , [4] или восьмиугольным шпинделем , [5], поскольку он имеет восемь четырехугольных граней и однозначно определяется как комбинаторный многогранник этим свойством. [3] Добавление четырех кубоидов к сетке для кубического октаэдра также даст сетку для пирамиды Шнайдерса. [2] Как односвязный многогранник с четным числом четырехугольных граней, кубический октаэдр может быть разложен на топологические кубоиды с изогнутыми гранями, которые встречаются лицом к лицу без подразделения граничных четырехугольников, [1] [5] [6] и была построена явная сетка этого типа. [4] Однако неясно, можно ли получить разложение этого типа, в котором все кубоиды являются выпуклыми многогранниками с плоскими гранями. [1] [5]
В искусстве
Четырехугольный трапецоэдр изображен в верхнем левом углу как одна из многогранных «звезд» на гравюре на дереве М. К. Эшера «Звезды » 1948 года .
Сферическая мозаика
Тетрагональный трапецоэдр также существует в виде сферической мозаики с двумя вершинами на полюсах и чередующимися вершинами, равномерно расположенными выше и ниже экватора.
Связанные многогранники
| Имя трапецоэдра | Двуугольный трапецоэдр ( Тетраэдр ) | Треугольный трапецоэдр | Тетрагональный трапецоэдр | Пятиугольный трапецоэдр | Шестиугольный трапецоэдр | ... | Апейрогональный трапецоэдр |
|---|---|---|---|---|---|---|---|
| Изображение многогранника |  |  |  |  |  | ... | |
| Сферическое мозаичное изображение |  |  |  |  |  | Изображение мозаики плоскости |  |
| Конфигурация лица | В2.3.3.3 | В3.3.3.3 | В4.3.3.3 | В5.3.3.3 | В6.3.3.3 | ... | В∞.3.3.3 |
Тетрагональный трапецоэдр является первым в серии двойных плосконосых многогранников и мозаик с конфигурацией граней V3.3.4.3. n .
| 4 n 2 мутации симметрии плосконосых мозаик: 3.3.4.3. n | ||||||||
|---|---|---|---|---|---|---|---|---|
| Симметрия 4 н 2 | Сферический | Евклидов | Компактный гиперболический | Паракомп. | ||||
| 242 | 342 | 442 | 542 | 642 | 742 | 842 | ∞42 | |
| Курносые фигуры |  |  |  |  |  |  |  |  |
| Конфигурация. | 3.3.4.3.2 | 3.3.4.3.3 | 3.3.4.3.4 | 3.3.4.3.5 | 3.3.4.3.6 | 3.3.4.3.7 | 3.3.4.3.8 | 3.3.4.3.∞ |
Фигурки гироскопа |  |  |  |  | ||||
| Конфигурация. | В3.3.4.3.2 | В3.3.4.3.3 | В3.3.4.3.4 | В3.3.4.3.5 | В3.3.4.3.6 | В3.3.4.3.7 | В3.3.4.3.8 | В3.3.4.3.∞ |
Ссылки
- ^ abc Эппштейн, Дэвид (1996), «Генерация гексаэдрической сетки линейной сложности», Труды Двенадцатого ежегодного симпозиума по вычислительной геометрии (SCG '96) , Нью-Йорк, США: ACM, стр. 58–67 , arXiv : cs/9809109 , doi :10.1145/237218.237237, ISBN 0-89791-804-5, MR 1677595, S2CID 3266195.
- ^ ab Mitchell, SA (1999), "Шаблон геоды, состоящий из шестиугольников, для согласования сетки тетраэдра, нарезанной кубиками, с любой сеткой гексаэдра, нарезанной кубиками", Engineering with Computers , 15 (3): 228– 235, doi :10.1007/s003660050018, S2CID 3236051.
- ^ abc Шварц, Александр ; Циглер, Гюнтер М. (2004), «Методы построения кубических комплексов, нечетных кубических 4-многогранников и предписанных дуальных многообразий», Experimental Mathematics , 13 (4): 385–413 , arXiv : math/0310269 , CiteSeerX 10.1.1.408.1550 , doi :10.1080/10586458.2004.10504548, MR 2118264, S2CID 1741871 .
- ^ abc Карбонера, Карлос Д.; Шеперд, Джейсон Ф.; Шеперд, Джейсон Ф. (2006), «Конструктивный подход к построению ограниченной гексаэдральной сетки», Труды 15-го Международного круглого стола по сеткам , Берлин: Springer, стр. 435–452 , doi :10.1007/978-3-540-34958-7_25, ISBN 978-3-540-34957-0.
- ^ abcd Эриксон, Джефф (2013), «Эффективное создание гексагональных сеток с использованием топологии», Труды Двадцать девятого ежегодного симпозиума по вычислительной геометрии (SoCG '13) (PDF) , Нью-Йорк, США: ACM, стр. 37–46 , doi :10.1145/2462356.2462403, ISBN 978-1-4503-2031-3, S2CID 10861924, заархивировано из оригинала (PDF) 2017-08-10 , извлечено 2014-07-21.
- ^ Митчелл, Скотт А. (1996), «Характеристика четырехугольных сеток поверхности, допускающих совместимую гексаэдральную сетку замкнутого объема», STACS 96: 13-й ежегодный симпозиум по теоретическим аспектам компьютерной науки Гренобль, Франция, 22–24 февраля 1996 г., Труды, заметки лекций по компьютерной науке, т. 1046, Берлин: Springer, стр. 465–476 , doi :10.1007/3-540-60922-9_38, ISBN 978-3-540-60922-3, МР 1462118.
Внешние ссылки
- Бумажная модель тетрагонального (квадратного) трапецоэдра
- Вайсштейн, Эрик В. «Трапецоэдр». MathWorld .

