Аксиомы Тарского

Аксиомы Тарского являются системой аксиом для евклидовой геометрии , в частности для той части евклидовой геометрии, которая формулируется в логике первого порядка с тождеством (т.е. формулируется как элементарная теория ). Как таковая, она не требует базовой теории множеств . Единственными примитивными объектами системы являются «точки», а единственными примитивными предикатами являются «промежуточность» (выражающая тот факт, что точка лежит на отрезке прямой между двумя другими точками) и «конгруэнтность» (выражающая тот факт, что расстояние между двумя точками равно расстоянию между двумя другими точками). Система содержит бесконечно много аксиом.

Система аксиом принадлежит Альфреду Тарскому , который впервые представил ее в 1926 году. ^[1] Другими современными аксиомизациями евклидовой геометрии являются аксиомы Гильберта (1899) и аксиомы Биркгофа (1932).

Используя свою систему аксиом, Тарский смог показать, что теория первого порядка евклидовой геометрии является последовательной , полной и разрешимой : каждое предложение в ее языке либо доказуемо, либо опровергаемо с помощью аксиом, и у нас есть алгоритм, который решает для любого данного предложения, доказуемо оно или нет.

В начале своей карьеры Тарский преподавал геометрию и исследовал теорию множеств. Его коллега Стивен Гиван (1999) объяснил отправную точку Тарского:

От Энрикеса Тарский узнал о работе Марио Пьери , итальянского геометра, на которого сильное влияние оказал Пеано. Тарский предпочитал систему Пьери [его мемуаров «Точка и сфера» ], где логическая структура и сложность аксиом были более прозрачными.

Затем Гиван говорит, что Тарский «с присущей ему тщательностью» разработал свою систему:

Чем отличался подход Тарского к геометрии? Прежде всего, система аксиом была намного проще любой из систем аксиом, существовавших до того времени. Фактически, длина всех аксиом Тарского вместе взятых не намного больше, чем длина одной из 24 аксиом Пьери. Это была первая система евклидовой геометрии, которая была достаточно проста для того, чтобы все аксиомы можно было выразить только с помощью примитивных понятий , без помощи определенных понятий. Еще важнее то, что впервые было проведено четкое различие между полной геометрией и ее элементарной — то есть ее первой порядковой — частью.

Как и другие современные аксиоматизации евклидовой геометрии, Тарский использует формальную систему, состоящую из строк символов, называемых предложениями , конструкция которых соблюдает формальные синтаксические правила и правила доказательства, которые определяют допустимые манипуляции предложениями. В отличие от некоторых других современных аксиоматизаций, таких как аксиоматизации Биркгофа и Гильберта , аксиоматизация Тарского не имеет примитивных объектов, кроме точек , поэтому переменная или константа не может ссылаться на линию или угол. Поскольку точки являются единственными примитивными объектами, а система Тарского является теорией первого порядка , невозможно даже определить линии как наборы точек. Единственными примитивными отношениями ( предикатами ) являются «промежуточность» и «конгруэнтность» между точками.

Аксиоматизация Тарского короче, чем у конкурентов, в том смысле, в котором Тарский и Дживант (1999) это ясно выразили. Она более лаконична, чем у Пьери, потому что у Пьери было только два примитивных понятия, в то время как у Тарского было три: точка, промежуточность и конгруэнтность. Такая экономия примитивных и определенных понятий означает, что система Тарского не очень удобна для выполнения евклидовой геометрии. Скорее, Тарский разработал свою систему для облегчения ее анализа с помощью инструментов математической логики , т. е. для облегчения вывода ее метаматематических свойств. Система Тарского обладает необычным свойством, заключающимся в том, что все предложения могут быть записаны в универсально-экзистенциальной форме, частном случае предваренной нормальной формы . В этой форме все универсальные кванторы предшествуют любым экзистенциальным кванторам , так что все предложения могут быть переписаны в форме Этот факт позволил Тарскому доказать, что евклидова геометрия разрешима : существует алгоритм , который может определить истинность или ложность любого предложения. Аксиоматизация Тарского также является полной . Это не противоречит первой теореме Гёделя о неполноте , поскольку теория Тарского не обладает выразительной силой, необходимой для интерпретации арифметики Робинсона (Franzén 2005, стр. 25–26).${\displaystyle \forall u\forall v\ldots \exists a\exists b\dots .}$

Альфред Тарский работал над аксиоматизацией и метаматематикой евклидовой геометрии с перерывами с 1926 года до своей смерти в 1983 году, причем Тарский (1959) возвестил о его зрелом интересе к предмету. Работа Тарского и его учеников по евклидовой геометрии достигла кульминации в монографии Швабхойзер, Шмелев и Тарский (1983), в которой изложены 10 аксиом и одна схема аксиом, показанная ниже, связанная с ними метаматематика и значительная часть предмета. Гупта (1965) внес важный вклад, а Тарский и Гивант (1999) обсуждают историю.

Эти аксиомы являются более элегантной версией множества, разработанного Тарским в 1920-х годах в рамках его исследования метаматематических свойств евклидовой геометрии на плоскости . Эта цель требовала переформулировать эту геометрию как теорию первого порядка . Тарский сделал это , постулируя вселенную точек , где строчные буквы обозначали переменные, ранжирующиеся по этой вселенной. Равенство обеспечивается базовой логикой (см. Логика первого порядка#Равенство и ее аксиомы ). ^[2] Затем Тарский постулировал два примитивных отношения:

• Промежуточность , триадическое отношение . Атомарное предложение Bxyz обозначает, что точка y находится «между» точками x и z , другими словами, что y является точкой на отрезке xz . (Это отношение интерпретируется включительно, так что Bxyz тривиально истинно всякий раз, когда x=y или y=z ).
• Конгруэнтность (или «равноудалённость»), тетрадическое отношение . Атомарное предложение Cwxyz или обычно wx ≡ yz можно интерпретировать как wx конгруэнтно yz ,другими словами , что длина отрезка wx равна длине отрезка yz .

Промежуточность охватывает аффинный аспект (такой как параллельность линий) евклидовой геометрии; конгруэнтность — ее метрический аспект (такой как углы и расстояния). Фоновая логика включает тождество — бинарное отношение , обозначаемое как =.

Аксиомы ниже сгруппированы по типам отношений, которые они вызывают, затем отсортированы, сначала по количеству квантификаторов существования, затем по количеству атомарных предложений. Аксиомы следует читать как универсальные замыкания ; следовательно, любые свободные переменные следует считать неявно универсально квантифицированными .

Рефлексивность Конгруэнтности

${\displaystyle xy\equiv yx\,.}$

Идентичность соответствия

${\displaystyle xy\equiv zz\rightarrow x=y.}$

Транзитивность конгруэнтности

${\displaystyle (xy\equiv zu\land xy\equiv vw)\rightarrow zu\equiv vw.}$

Хотя формально отношение конгруэнтности является 4-сторонним отношением между точками, неформально его можно рассматривать как бинарное отношение между двумя отрезками и . Аксиомы «рефлексивности» и «транзитивности», указанные выше, в совокупности доказывают оба:${\displaystyle xy\equiv zw}$${\displaystyle xy}$${\displaystyle zw}$

• что это бинарное отношение на самом деле является отношением эквивалентности
  • это рефлексивно: .${\displaystyle xy\equiv xy}$
  • он симметричен .${\displaystyle xy\equiv zw\rightarrow zw\equiv xy}$
  • это переходно .${\displaystyle (xy\equiv zu\land zu\equiv vw)\rightarrow xy\equiv vw}$
• и что порядок, в котором указаны точки отрезка линии, не имеет значения.
  • ${\displaystyle xy\equiv zw\rightarrow xy\equiv wz}$.
  • ${\displaystyle xy\equiv zw\rightarrow yx\equiv zw}$.
  • ${\displaystyle xy\equiv zw\rightarrow yx\equiv wz}$.

Аксиома «транзитивности» утверждает, что конгруэнтность является евклидовой , поскольку она соответствует первому из « общих понятий » Евклида .

Аксиома «Идентичность конгруэнтности» интуитивно утверждает, что если xy конгруэнтен отрезку, который начинается и заканчивается в одной и той же точке, то x и y являются одной и той же точкой. Это тесно связано с понятием рефлексивности для бинарных отношений .

Идентичность промежуточности

${\displaystyle Bxyx\rightarrow x=y.}$

Единственная точка на отрезке — это он сам.${\displaystyle xx}$${\displaystyle x}$

Аксиома Пасхи

${\displaystyle (Bxuz\land Byvz)\rightarrow \exists a\,(Buay\land Bvax).}$

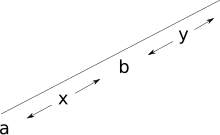
Аксиоматическая схема непрерывности

Пусть φ( x ) и ψ( y ) — формулы первого порядка , не содержащие свободных экземпляров a или b . Пусть также не будет свободных экземпляров x в ψ( y ) или y в φ( x ) . Тогда все экземпляры следующей схемы являются аксиомами:

${\displaystyle \exists a\,\forall x\,\forall y\,[(\phi (x)\land \psi (y))\rightarrow Baxy]\rightarrow \exists b\,\forall x\,\forall y\,[(\phi (x)\land \psi (y))\rightarrow Bxby].}$

Пусть r — луч с конечной точкой a . Пусть формулы первого порядка φ и ψ определяют подмножества X и Y множества r , такие, что каждая точка в Y находится справа от каждой точки X (относительно a ). Тогда существует точка b в r, лежащая между X и Y. По сути, это конструкция разреза Дедекинда , выполненная таким образом, чтобы избежать квантификации по множествам.

Обратите внимание, что формулы φ( x ) и ψ( y ) могут содержать параметры, т.е. свободные переменные, отличные от a , b , x, y . И действительно, каждый пример схемы аксиом, который не содержит параметров, может быть доказан из других аксиом. ^[3]

Нижнее измерение

${\displaystyle \exists a\,\exists b\,\exists c\,[\neg Babc\land \neg Bbca\land \neg Bcab].}$

Существуют три неколлинеарные точки. Без этой аксиомы теория могла бы быть смоделирована одномерной действительной линией , одной точкой или даже пустым множеством.

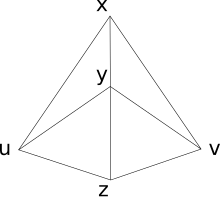
Верхнее измерение

${\displaystyle (xu\equiv xv)\land (yu\equiv yv)\land (zu\equiv zv)\land (u\neq v)\rightarrow (Bxyz\lor Byzx\lor Bzxy).}$

Три точки, равноудалённые от двух различных точек, образуют линию. Без этой аксиомы теория могла бы быть смоделирована трёхмерным или более многомерным пространством.

Аксиома Евклида

Можно привести три варианта этой аксиомы, обозначенные ниже как A, B и C. Они эквивалентны друг другу с учетом остальных аксиом Тарского и, безусловно, эквивалентны постулату параллельности Евклида .

А :${\displaystyle ((Bxyw\land xy\equiv yw)\land (Bxuv\land xu\equiv uv)\land (Byuz\land yu\equiv uz))\rightarrow yz\equiv vw.}$

Пусть отрезок линии соединяет середины двух сторон данного треугольника . Этот отрезок линии будет вдвое короче третьей стороны. Это эквивалентно сумме внутренних углов любого треугольника в два прямых угла .

Б :${\displaystyle Bxyz\lor Byzx\lor Bzxy\lor \exists a\,(xa\equiv ya\land xa\equiv za).}$

Для любого треугольника существует окружность , включающая все его вершины.

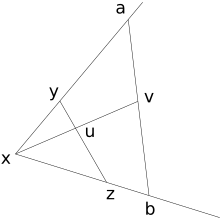
С :${\displaystyle (Bxuv\land Byuz\land x\neq u)\rightarrow \exists a\,\exists b\,(Bxya\land Bxzb\land Bavb).}$

Для любого угла и любой точки v внутри него существует отрезок прямой, включающий v , с конечными точками на каждой стороне угла.

Каждый вариант имеет преимущество перед другими:

• А обходится без экзистенциальных квантификаторов ;
• B имеет наименьшее количество переменных и атомарных предложений ;
• C требует только одного примитивного понятия, промежуточности. Этот вариант является обычным, приведенным в литературе.

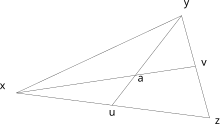
Пять сегментов

${\displaystyle {(x\neq y\land Bxyz\land Bx'y'z'\land xy\equiv x'y'\land yz\equiv y'z'\land xu\equiv x'u'\land yu \equiv y'u')}\rightarrow zu\equiv z'u'.}$

Начните с двух треугольников , xuz и x'u'z'. Нарисуйте отрезки yu и y'u', соединяющие вершину каждого треугольника с точкой на стороне, противоположной вершине. Результатом будут два разделенных треугольника, каждый из которых состоит из пяти отрезков. Если четыре отрезка одного треугольника каждый конгруэнтны отрезку в другом треугольнике, то пятые отрезки в обоих треугольниках должны быть конгруэнтны.

Это эквивалентно правилу «сторона-угол-сторона» для определения того, что два треугольника равны; если углы uxz и u'x'z' равны (существуют равные треугольники xuz и x'u'z' ), и две пары инцидентных сторон равны ( xu ≡ x'u' и xz ≡ x'z' ), то оставшаяся пара сторон также равна ( uz ≡ u'z' ).

Строительство сегмента

${\displaystyle \exists z\,[Bxyz\land yz\equiv ab].}$

Для любой точки y можно провести в любом направлении (определяемом x ) линию, конгруэнтную любому отрезку ab .

Согласно Тарскому и Дживанту (1999: 192-93), ни одна из вышеперечисленных аксиом не является принципиально новой. Первые четыре аксиомы устанавливают некоторые элементарные свойства двух примитивных отношений. Например, рефлексивность и транзитивность конгруэнтности устанавливают, что конгруэнтность является отношением эквивалентности над отрезками прямых. Тождество конгруэнтности и промежуточности управляют тривиальным случаем, когда эти отношения применяются к неразличимым точкам. Теорема xy ≡ zz ↔ x = y ↔ Bxyx расширяет эти аксиомы тождества.

Ряд других свойств промежуточности можно вывести в виде теорем ^[4], включая:

• Рефлексивность : Bxxy  ;
• Симметрия : Bxyz → Bzyx  ;
• Транзитивность : ( Bxyw ∧ Byzw ) → Bxyz  ;
• Связность : ( Bxyw ∧ Bxzw ) → ( Bxyz ∨ Bxzy ).

Последние два свойства полностью упорядочивают точки, составляющие отрезок прямой.

Аксиомы верхнего и нижнего измерений вместе требуют, чтобы любая модель этих аксиом имела размерность 2, т. е. чтобы мы аксиоматизировали евклидову плоскость. Подходящие изменения в этих аксиомах дают наборы аксиом для евклидовой геометрии для размерностей 0, 1 и больше 2 (Tarski and Givant 1999: Axioms 8 ⁽¹⁾ , 8 ⁽ⁿ⁾ , 9 ⁽⁰⁾ , 9 ⁽¹⁾ , 9 ⁽ⁿ⁾ ). Обратите внимание, что стереометрия не требует новых аксиом, в отличие от случая с аксиомами Гильберта . Более того, нижнее измерение для n измерений является просто отрицанием верхнего измерения для n - 1 измерений.

Когда число измерений больше 1, промежуточность может быть определена в терминах конгруэнтности (Tarski and Givant, 1999). Сначала определим отношение "≤" (где интерпретируется как "длина отрезка линии меньше или равна длине отрезка линии "):${\displaystyle ab\leq cd}$${\displaystyle ab}$${\displaystyle компакт-диск}$

${\displaystyle xy\leq zu\leftrightarrow \forall v(zv\equiv uv\rightarrow \exists w(xw\equiv yw\land yw\equiv uv)).}$

В случае двух измерений интуиция такова: для любого отрезка xy рассмотрим возможный диапазон длин xv , где v — любая точка на перпендикуляре к биссектрисе xy . Очевидно, что, хотя верхней границы длины xv не существует , нижняя граница существует, когда v является средней точкой xy . Таким образом, если xy короче или равен zu , то диапазон возможных длин xv будет надмножеством диапазона возможных длин zw , где w — любая точка на перпендикуляре к биссектрисе zu .

Промежуточность можно тогда определить, используя интуитивное представление о том, что кратчайшее расстояние между любыми двумя точками — это прямая линия:

${\displaystyle Bxyz\leftrightarrow \forall u((ux\leq xy\land uz\leq zy)\rightarrow u=y).}$

Схема аксиом непрерывности гарантирует, что упорядочение точек на линии является полным (относительно определяемых свойств первого порядка). Как было отмечено Тарским, эта схема аксиом первого порядка может быть заменена более мощной аксиомой второго порядка непрерывности, если разрешить переменным ссылаться на произвольные наборы точек. Полученная система второго порядка эквивалентна набору аксиом Гильберта. (Тарский и Живант, 1999)

Аксиомы Паша и Евклида хорошо известны. Аксиома построения отрезка делает возможным измерение и декартову систему координат — просто присвойте длину 1 некоторому произвольному непустому отрезку прямой. Действительно, в (Schwabhäuser 1983) показано, что, указав две выделенные точки на прямой, называемые 0 и 1, мы можем определить сложение, умножение и упорядочение, превращая множество точек на этой прямой в действительно замкнутое упорядоченное поле . Затем мы можем ввести координаты из этого поля, показывая, что каждая модель аксиом Тарского изоморфна двумерной плоскости над некоторым действительно замкнутым упорядоченным полем.

Стандартные геометрические понятия параллельности и пересечения прямых (где прямые представлены двумя различными точками на них), прямых углов, равенства углов, подобия треугольников, касания прямых и окружностей (представленных центральной точкой и радиусом) могут быть определены в системе Тарского.

Пусть wff обозначает правильно сформированную формулу (или синтаксически правильную формулу первого порядка) в системе Тарского. Тарский и Живант (1999: 175) доказали, что система Тарского:

• Последовательность : не существует такого wff, что и оно, и его отрицание могут быть доказаны из аксиом;
• Полнота : каждое утверждение или его отрицание является теоремой, доказуемой из аксиом;
• Decidable : Существует алгоритм , который решает для каждого wff, является ли он доказуемым или опровергаемым из аксиом. Это следует из Тарского:
  • Процедура принятия решения для действительного замкнутого поля , которую он нашел методом исключения кванторов ( теорема Тарского–Зейденберга );
  • Аксиомы, допускающие указанное выше представление в виде двумерной плоскости над действительным замкнутым полем .

Это имеет следствие, что каждое утверждение (второго порядка, общее) евклидовой геометрии, которое может быть сформулировано как предложение первого порядка в системе Тарского, является истинным тогда и только тогда, когда оно доказуемо в системе Тарского, и эта доказуемость может быть автоматически проверена с помощью алгоритма Тарского. Это, например, применимо ко всем теоремам в « Началах» Евклида , Книга I. Примером теоремы евклидовой геометрии, которая не может быть сформулирована таким образом, является свойство Архимеда : для любых двух отрезков прямой положительной длины S ₁ и S ₂ существует натуральное число n такое, что nS ₁ длиннее, чем S ₂ . (Это является следствием того факта, что существуют действительно замкнутые поля, содержащие бесконечно малые числа. ^[5] ) Другие понятия, которые не могут быть выражены в системе Тарского, являются конструктивность с помощью линейки и циркуля и утверждения, которые говорят о «всех многоугольниках» и т. д. ^[6]

Гупта (1965) доказал независимость аксиом Тарского, за исключением аксиом Паша и рефлексивности конгруэнтности .

Отрицание Аксиомы Евклида даёт гиперболическую геометрию , а её полное устранение даёт абсолютную геометрию . Полная (в отличие от элементарной) Евклидова геометрия требует отказа от аксиоматизации первого порядка: заменить φ( x ) и ψ( y ) в схеме аксиом Непрерывности на x ∈ A и y ∈ B , где A и B — универсально квантифицированные переменные, пробегающие множества точек.

Аксиомы Гильберта для плоской геометрии номер 16 и включают транзитивность конгруэнтности и вариант аксиомы Паша. Единственное понятие из интуитивной геометрии, упомянутое в замечаниях к аксиомам Тарского, — это треугольник . (Версии B и C аксиомы Евклида ссылаются на «окружность» и «угол» соответственно.) Аксиомы Гильберта также требуют «луча», «угла» и понятия треугольника, «включающего» угол. В дополнение к промежуточности и конгруэнтности аксиомы Гильберта требуют примитивного бинарного отношения «на», связывающего точку и прямую.

Гильберт использует две аксиомы Непрерывности, и они требуют логики второго порядка . Напротив, схема аксиом Непрерывности Тарского состоит из бесконечного числа аксиом первого порядка. Такая схема необходима; Евклидова геометрия на языке Тарского (или эквивалентном) не может быть конечно аксиоматизирована как теория первого порядка .

Система Гильберта, таким образом, значительно сильнее: каждая модель изоморфна реальной плоскости (используя стандартные понятия точек и линий). Напротив, система Тарского имеет много неизоморфных моделей: для каждого действительно замкнутого поля F плоскость F ² предоставляет одну такую ​​модель (где промежуточность и конгруэнтность определяются очевидным образом). ^[7]${\displaystyle \mathbb {R} ^{2}}$

Первые четыре группы аксиом Гильберта для плоской геометрии являются двуинтерпретируемыми с аксиомами Тарского минус непрерывность.

• Евклидова геометрия
• Евклидово пространство

• Францен, Торкель (2005), Теорема Гёделя: неполное руководство по ее использованию и злоупотреблению , AK Peters, ISBN 1-56881-238-8
• Дживант, Стивен (1 декабря 1999 г.). «Объединяющие нити в работах Альфреда Тарского». The Mathematical Intelligencer . 21 (1): 47–58. doi :10.1007/BF03024832. ISSN  1866-7414. S2CID  119716413.
• Гринберг, Марвин Джей (2010). «Старые и новые результаты в основах элементарной плоской евклидовой и неевклидовой геометрии» (PDF) . The American Mathematical Monthly . 117 (3): 198. doi :10.4169/000298910x480063.
• Гупта, Х. Н. (1965). Вклад в аксиоматические основы геометрии (диссертация доктора философии). Калифорнийский университет в Беркли.
• Tarski, Alfred (1959), "Что такое элементарная геометрия?", в Leon Henkin, Patrick Suppes и Alfred Tarski (ред.), Аксиоматический метод. С особым акцентом на геометрию и физику. Труды Международного симпозиума, проведенного в Калифорнийском университете в Беркли, 26 декабря 1957 г. - 4 января 1958 г. , Исследования по логике и основаниям математики, Амстердам: Северная Голландия, стр. 16–29, MR  0106185.
  • Доступно как переиздание 2007 г., Brouwer Press, ISBN 1-4437-2812-8 
• Тарский, Альфред ; Дживант, Стивен (1999), «Система геометрии Тарского», The Bulletin of Symbolic Logic , 5 (2): 175–214, CiteSeerX  10.1.1.27.9012 , doi :10.2307/421089, ISSN  1079-8986, JSTOR  421089, MR  1791303, S2CID  18551419
• Швабхойзер, В.; Шмелев, В. ; Тарский, Альфред (1983). Метаматематические методы в геометрии . Спрингер-Верлаг.
• Щерба, Л. В. (1986). «Тарский и геометрия» (PDF) . Журнал символической логики . 51 (4): 907–12. doi :10.2307/2273904. JSTOR  2273904. S2CID  35275962.