Обсуждение:Сферические гармоники

Эта статья уровня 5 жизненно важна и имеет рейтинг B-класса по шкале оценки контента Википедии . Она представляет интерес для следующих WikiProjects :

Математика Средний приоритет Эта статья находится в рамках WikiProject Mathematics , совместных усилий по улучшению освещения математики в Википедии. Если вы хотите принять участие, посетите страницу проекта, где вы можете присоединиться к обсуждению и увидеть список открытых задач.Математика Википедия:WikiProject Mathematics Шаблон:WikiProject Mathematics математика Середина Данная статья имеет средний уровень приоритетности по шкале приоритетов проекта . Физика средней важности Эта статья находится в рамках WikiProject Physics , совместных усилий по улучшению освещения физики в Википедии. Если вы хотите принять участие, посетите страницу проекта, где вы можете присоединиться к обсуждению и увидеть список открытых задач.PhysicsWikipedia:WikiProject PhysicsTemplate:WikiProject Physicsphysics Mid This article has been rated as Mid-importance on the project's importance scale. Geology Start‑class Mid‑importance This article is within the scope of WikiProject Geology, an attempt at creating a standardized, informative, comprehensive and easy-to-use geology resource. If you would like to participate, you can choose to edit this article, or visit the project page for more information.GeologyWikipedia:WikiProject GeologyTemplate:WikiProject GeologyGeology Start This article has been given a rating which conflicts with the project-independent quality rating in the banner shell. Please resolve this conflict if possible. Mid This article has been rated as Mid-importance on the project's importance scale.

Рисунок вверху справа с 3D-визуализацией функций, по-видимому, неверен. Все отрицательные порядковые (отрицательные m) рисунки просто такие же, как для эквивалентного положительного m, но с изменением знака, если m нечетное. На самом деле их следует повернуть вокруг оси на 90 градусов. То же самое, по-видимому, происходит и на большом цветном рисунке внизу справа.

CWHughes (обс.) 13:51, 4 мая 2012 (UTC) [ ответить ]

Гармоники явно нарисованы неправильно, хотя я не уверен, что согласен насчет точной угловой ошибки. Может быть, кто-то уже пытался это исправить (но не полностью)?

Для очевидной ошибки обратите внимание, что первая и пятая сферические гармоники, показанные в третьей строке, в настоящее время идентичны. Аналогично для четвертой строки.

Далее, все графики кажутся «сплющенными». Должны ли графики быть сферическими полярными графиками? Если так, то все элементы во второй строке должны выглядеть как две соприкасающиеся сферы. — Предыдущий неподписанный комментарий добавлен 92.234.82.157 ( обсуждение ) 16:26, 3 октября 2013 (UTC) [ ответить ]

Я реализовал правильный SH, следуя Википедии, и получил следующий рендер: https://commons.wikimedia.org/wiki/File:Spherical_Harmonics.png

Я думаю, что некоторые функции SH выглядят одинаково из-за перспективной проекции. Вот код для рендерера, если хотите взглянуть: https://www.shadertoy.com/view/lsfXWH

Я думаю, что мой рендер выглядит лучше в целом, он более читаем с точки зрения формы и освещения? Стоит ли заменить текущую картинку на эту? — Предыдущий неподписанный комментарий добавлен Inigo.quilez ( talk • contribs ) 02:36, 15 мая 2014 (UTC) [ ответить ]

Я могу подтвердить, что некоторые из них неверны, и это не проблема проекции (если только вы не хотите сказать, что вы меняете проекцию с m на -m). Я не вижу того, что вы выложили, но l=2, m=+-2 должны быть друг напротив друга (поменяйте местами синюю и желтую области). То же самое касается l=3,m=+-2. Но хорошая цифра. Jazzwhiz101 (обсуждение) 19:27, 29 мая 2014 (UTC) [ ответить ]

Гармоники m=2 и m=-2 на самом деле являются комплексно сопряженными друг другу, и их действительные части идентичны. Поскольку визуализация показывает только действительные компоненты, они верны, но они «вращаются» в противоположных направлениях, если вы продвигаете фазу. То, что вы предлагаете относительно переключения синего и желтого, можно достичь путем отрицания этих гармоник. Таким образом, перевернутая версия синего и желтого не ортогональна неперевернутой версии. Это мнимая составляющая делает их ортогональными. Таким образом, то, что вы предлагаете, не является неверным, но это не обязательно, и визуализации правильно отражают гармоники, как они представлены в статье. Я полагаю, это является результатом выбора представления гармоник в соответствии с соглашением о фазах Кондона-Шортли.

На большом изображении цветного участка внизу есть опечатка. Вторая сфера сверху слева обозначена (5,4), тогда как должна быть обозначена (5,1). Тот, кто создал изображение, пожалуйста, исправьте ее.

Отредактировал это:

«С этим расширением очень тесно связана алгебро-геометрическая интерпретация 2-сферы как действительной коммутативной алгебры, порожденной a, b и c при соблюдении соотношения a ² +b ² +c ² -1=0, или интерпретация C* как алгебры C*, порожденной самосопряженными элементами a, b и c при соблюдении соотношения a ² +b ² +c ² -1=0».

Я не вижу тесной связи. Сферические гармоники имеют элитное объяснение из теории представлений; но это (пока) не оно.

Чарльз Мэтьюз 12:52, 23 октября 2003 (UTC)

Пожалуйста, рассмотрите возможность создания отдельной статьи, возможно, Таблицы сферических гармоник , которая будет содержать список явных выражений для l>4. Хотя такая таблица не слишком полезна, она может пригодиться, если кто-то просто хочет взглянуть на что-то и не хочет писать программное обеспечение для решения какого-то частного случая. linas 22:55, 16 августа 2005 (UTC) [ ответить ]

Я уже создал таблицу, просто закомментировал большую ее часть, поэтому самым сложным было сохранить ее без сообщения об ошибке типа «Что-то не вернуло ответ на ваш запрос». Κσυπ Cyp   06:38, 20 августа 2005 (UTC) [ ответить ]

Да, WP недавно выдал это сообщение об ошибке. Я обнаружил, что довольно часто изменения действительно попадали в базу данных, но веб-страница не отображалась. Таким образом, если вы откроете второй браузер и загрузите страницу, вы (обычно) увидите, что ваши изменения были внесены. Так что вам не придется нажимать кнопку отправки снова и снова. linas 16:54, 20 августа 2005 (UTC) [ ответить ]

Я добавил ссылку на [Варшаловича и др.]. Эта книга содержит сотни страниц таблиц и формул по сферическим гармоникам и может быть очень полезна.

Ален Мишо 16:47, 31 октября 2005 (UTC)

В угловой части уравнения Лапласа указан индекс l. Мне кажется естественным записать вторую формулу, показывающую индекс m, чтобы направлять читателя. В настоящее время индекс m довольно внезапно появился в обозначении общего решения и в неравенстве - l<..< m <..<+l.

Я мог бы предложить заменить название азимутального угла «фи» на «тета» в целях соответствия правилам пространственной ориентации.

Может быть, индексам l и m здесь можно было бы дать интуитивную геометрическую интерпретацию, до квантово-механических интерпретаций волнового уравнения Шредингера l и m, как целым числам, связанным с импульсным моментом и его проекцией в стандартном ('z')-направлении.

Последнее предложение: сравните решения Лапласа с решениями волнового уравнения Шредингера для центрального потенциала (например, кулоновского поля), чтобы обсудить различия и общие аспекты для радиально-угловых частей их решений.

Ганс ван дер Грифт

Я добавил определения для единичной мощности и полунормализованных по Шмидту сферических гармоник. Другие изменения были сделаны для обеспечения согласованности и точности. Я также добавил ссылки на архивы программного обеспечения, которые в настоящее время разрабатываются.

Примечание: Нам нужно упомянуть, используют ли аналитические выражения для первых нескольких сферических гармоник фазу Кондона-Шортли или нет. Действительно, это следует тщательно прояснить в ссылке на связанные функции Лежандра.

Марк Вечорек, 26 октября 2006 г.

«Фаза, необходимая для справедливости этого комплексного отношения сопряжения, — это так называемая фаза Кондона и Шортли».${\displaystyle Y_{\ell }^{m}}$

Я не думаю, что я согласен с этим. Я понимаю, что фаза Кондона-Шортли не имеет ничего общего с комплексным сопряжением — она исходит из тождества для отрицательного порядка, связанного с функциями Лежандра.

Я не согласен, другая фаза, так называемая фаза Рака, может быть распознана по , что согласуется с обычным определением обращения времени. Рака умножил Ylm на . Оба соглашения о фазах дают легко запоминающиеся формулы для операций повышения/понижения. Возможно, мне следовало бы сказать: соглашение CS может быть распознано по этому комплексному соотношению сопряжения. P.wormer${\displaystyle (Y_{\ell }^{m})^{*}=(-1)^{\ell +m}Y_{\ell }^{-m}\,}$${\displaystyle (i)^{\ell }}$

«В текстах, ориентированных на квантовую механику, фаза Кондона и Шортли обычно вводится в сферические гармонические функции. То есть, связанные с ней функции Лежандра определяются без фазы. Статья в Википедии определяет последние функции, включая фазу (-1)^m\, поэтому она правильно отсутствует в определении сферической гармонической функции в настоящей статье». ${\displaystyle (-1)^{m}\,}$

См. Edmonds, Messiah (vol I), Brink and Satchler, Biedenharn and Louck (и я мог бы упомянуть больше ссылок) для Plm без фазы. Мое любимое определение сферической гармоники — это то, которое не нуждается в Plm с отрицательным m, потому что Plm с отрицательным m несколько неестественно и требует нового определения. См. Altmann SL; Herzig P. Point-Group Theory Tables; Clarendon: Oxford, 1994. P.wormer

Я думаю, что нам нужен раздел, посвященный соглашению о фазах Кондона-Шортли, потому что это становится очень запутанным при обсуждении между дисциплинами. Некоторые физики помещают фазу в функцию Лежандра, тогда как некоторые добавляют ее к определению сферических гармонических функций. Некоторые дисциплины (например, геодезия и магнетизм) вообще не используют фазу CS. Честно говоря, я не уверен, зачем людям может понадобиться использовать эту фазу, и причину ее использования следует объяснить здесь. Я думаю, я слышал, что она упрощает операции с участием операторов лестничной логики, но я не уверен.

Да, операции лестницы (=шаг вверх/вниз) становятся проще, они становятся одинаковыми для положительных и отрицательных m. Без фазы CS (или Рака) необходимо различать знак m. P.wormer

Наконец, нам нужно отметить, используют ли аналитические выражения для Ylm фазу CS или нет. Поскольку я предполагаю, что этот раздел был написан физиком, то, вероятно, так и есть, be кто-то должен проверить. Lunokhod 04:18, 6 ноября 2006 (UTC) [ ответить ]

Статья в ее нынешнем виде меня вполне устраивает. P.wormer 13:15, 7 ноября 2006 (UTC) [ ответить ]

Извините, я безнадежный новичок в математике, но (цитата из статьи) «фазовый множитель (−1)m для m > 0, 1 в противном случае»: откуда взялось это условное выражение? У меня нет доступа к соответствующим исходным текстам, но во всех найденных мной случаях (в основном в работах по акустике с использованием сферических гармоник) упоминается простое, безусловное (-1)^m для всех m. Может кто-нибудь прояснить это? Nettings ( обс .) 20:41, 10 января 2014 (UTC) [ ответить ]

Теперь я в замешательстве, почему множитель (-1)^m есть и в определении сферических гармоник в квантовой механике, и в определении связанных с ними полиномов Лежандра? Мне это кажется неправильным. 200.57.50.123 (обсуждение) 21:11, 17 августа 2015 (UTC) [ ответить ]

Я думаю, что в определении квантовой механики нет (-1)^m. Если мы возьмем одну из приведенных ссылок, то они используют то же самое, что и в сейсмологии, я думаю. --Rafaelbernar (обс.) 20:55, 11 октября 2016 (UTC) [ ответить ]

В квантово-механическом определении должна быть фаза (−1) ^m , либо в самой сферической гармонике, либо встроенная в связанные полиномы Лежандра, но не в обоих случаях. В таком виде статья действительно сбивает с толку, поскольку в ней говорится о фазах без указания соглашения о фазах связанных полиномов Лежандра. Статья Википедии об связанных полиномах Лежандра уже включает фазу Кондона–Шортли, но, похоже, эта статья предполагает иное. Я рекомендую сделать эти две статьи согласованными друг с другом. Используйте P _ℓ ^m , если вы хотите встроенную фазу CS, и используйте P _{ℓ m,} если вы не хотите, чтобы фаза CS была включена в полиномы. Я исправил это для версии QM, но я ничего не знаю о соглашениях других полей. -- Fylwind ( обсуждение ) 02:14, 31 декабря 2017 (UTC) [ ответ ]

В статье в настоящее время утверждается, что «все вышеприведенные нормализованные сферические гармонические функции удовлетворяют» . Это строго верно в контексте, поскольку «все вышеприведенные нормализованные сферические гармонические функции» включают фазу CS один раз, либо внутри , либо как . Однако затем ниже кратко утверждается, что «сообщества геодезии и магнетизма никогда не включают фактор фазы Кондона–Шортли в свои определения сферических гармонических функций, ни в определения связанных полиномов Лежандра», что противоречит некоторым из этих «вышенормализованных» примеров. Если утверждение «ниже» верно, то соответствующие «выше» определения следует изменить, чтобы использовать без фазы CS, и эти случаи затем будут удовлетворять уравнению сопряжения также без фазы CS, т. е . .${\displaystyle Y_{\ell }^{m}{}^{*}=(-1)^{m}Y_{\ell }^{-m}}$${\displaystyle P_{\ell }^{m}}$${\displaystyle (-1)^{m}P_{\ell m}}$${\displaystyle P_{\ell m}}$${\displaystyle Y_{\ell }^{m}{}^{*}=Y_{\ell }^{-m}}$

Я удалил эту таблицу изображений. Я нахожу ее очень запутанной, и даже не уверен, какие координаты нанесены. Луноход 18:41, 16 ноября 2006 (UTC) [ ответить ]

Г 10
Г 20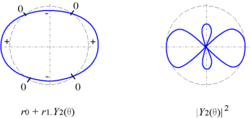
Г 30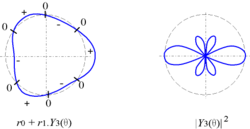

Никаких возражений — между небольшой анимацией вверху и графиком, показывающим разбиение поверхностей сфер по знаку, я думаю, можно получить довольно хорошее представление об этих функциях. Есть один график, показывающий поперечные сечения сферы, которые генерируют изображения, которые вы удалили; если ваши изображения не будут возвращены (чему я бы возражал), я также не вижу смысла в этом изображении. Я предлагаю удалить его тоже. Baccyak4H 18:58, 16 ноября 2006 (UTC) [ ответить ]

Обновление . Я удалил другое изображение. Baccyak4H 19:00, 16 ноября 2006 (UTC) [ ответить ]

Я думаю, что эта страница наконец-то в приличном состоянии. Однако, одна вещь, которая могла бы быть полезной, это список часто используемых тождеств, таких как интеграл трех гармоник, выраженный в коэффициентах Вигнера 3j и т. д. Я начну это, когда у меня будет время, но это низко в моем списке приоритетов. Есть ли еще что-то, чего не хватает? Lunokhod 18:53, 16 ноября 2006 (UTC) [ ответить ]

Преобразование (приведенное в этой статье) из комплексных в реальные сферические гармоники, если его применить к сферическим гармоникам Кондона-Шортли, даст m -зависимую фазу в реальных гармониках. Это неприятно. Если бы эта статья предназначалась только для квантовых механиков, я бы ее изменил. Но в других областях люди имеют разные мнения.-- P.wormer 15:06, 6 июля 2007 (UTC) [ ответить ]

Не будучи экспертом ни в этой области, ни в (фазовых) соглашениях, я думаю, что в определении действительных сферических гармоник есть ошибка: для отрицательных m Abs( m ) следует использовать последовательно, поэтому для отрицательных m Y_{\ell m} = {1\over i\sqrt2}\left(Y_\ell^{-m}-(-1)^{m}\, Y_\ell^{m}\right) = \sqrt{2} N_{(l,-m)} P_\ell^{-m}(\cos \theta) \sin -m\varphi . Я просто отмечаю несоответствие, кто-то с более глубокими знаниями в этой области должен это проверить. 86.61.67.116 (обсуждение) 10:55, 1 ноября 2008 (UTC) [ ответить ]

В определении действительно есть ошибка, как упоминалось выше. Попытался отредактировать его, но мне сказали ссылаться на источники. Я понятия не имею, как ссылаться на собственные вычисления. —Предыдущий неподписанный комментарий, добавленный 96.236.217.254 (обсуждение) 20:44, 10 марта 2009 (UTC) [ ответить ]

Еще один вопрос по части Real Spherical Harmonics. Почему бы нам просто не упростить определения, используя действительную и мнимую части:

${\displaystyle Y_{\ell m}={\begin{cases}{\sqrt {2}}\,\Re (Y_{\ell }^{m})={\sqrt {2}}N_{(\ell ,m)}P_{\ell }^{m}(\cos \theta )\cos m\varphi &{\mbox{if }}m>0\\Y_{\ell }^{0}&{\mbox{if }}m=0\\{\sqrt {2}}\,\Im (Y_{\ell }^{m})={\sqrt {2}}N_{(\ell ,|m|)}P_{\ell }^{|m|}(\cos \theta )\sin |m|\varphi &{\mbox{if }}m<0.\end{cases}}}$

Monsterman222 ( обсуждение ) 03:29, 5 марта 2013 (UTC) [ ответ ]

Кажется, я получил задание по очистке Pierre-Simon Laplace . Раздел Pierre-Simon Laplace#Сферические гармоники и теория потенциала требует внимания эксперта. Мне кажется, есть две проблемы:

1. Нет смысла объяснять, что такое сферические гармоники, лучше сделать это здесь; и
2. Определение (взятое из книги Рауз Болл « Краткий отчет об истории математики» (1908) ) не сразу показалось мне многообещающим.

Есть мысли, как переписать этот раздел? Cutler 00:03, 25 августа 2007 (UTC) [ ответить ]

Рауз Болл дает следующий отчет:

«Это памятно введением в анализ сферических гармоник или коэффициентов Лапласа , ...

«Если координаты двух точек равны ( r ,μ,ω) и ( r ′,μ',ω'), и если r ′ ≥ r , то обратная величина расстояния между ними может быть разложена по степеням r / r ′, а соответствующие коэффициенты являются коэффициентами Лапласа . Их полезность вытекает из того факта, что каждая функция координат точки на сфере может быть разложена в их ряд. Следует отметить, что аналогичные коэффициенты для пространства двух измерений вместе с некоторыми их свойствами были ранее приведены Адриеном-Мари Лежандром в статье, отправленной во Французскую академию в 1783 году . У Лежандра были веские основания жаловаться на то, как с ним обошлись в этом вопросе».

Кто-нибудь признает это как способ определения сферических гармоник? Если да, то это должно быть в статье. Cutler 10:09, 25 августа 2007 (UTC) [ ответить ]

В уравнении (13-17) квантовой теории атомной структуры, т. I , Слейтер определяет коэффициент, нормализованный как

${\displaystyle c^{k}(l,m,l,'m')={\sqrt {\frac {4\pi }{2k+1}}}\int d^{2}\Omega \ Y_{l}^{m}(\Omega )^{*}Y_{l'}^{m'}(\Omega )Y_{k}^{m-m'}(\Omega )}$

Бете и Джекив используют эту нормализацию в уравнении (4-48) из Intermediate Quantum Mechanics (1985), а Кондон и Шортли также используют ее на стр. 175 из The Theory of Atomic Spectra (1959).
-Брайан —Предыдущий неподписанный комментарий добавлен 128.97.23.22 (обсуждение) 16:22, 14 июля 2008 (UTC) [ ответить ]

Я думаю добавить раздел приложений. Пока что я думаю о сферических гармонических представлениях в геофизике, таких как:

• Гравитация
• Топография
• Планетарные магнитные поля

Если у кого-то еще есть что-то, что они могут посчитать приложением, пожалуйста, оставьте здесь заметку, чтобы раздел не стал предвзятым в пользу моей области знаний. Awickert ( обсуждение ) 04:56, 3 мая 2009 (UTC) [ ответ ]

Он активно используется в моделировании глобального освещения и некоторых других областях трехмерной компьютерной графики. Классическая компьютерная графика рассматривает источники света, такие как солнце и уличные фонари, как бесконечно малые точки, но для достижения наилучшего реализма вам необходимо включить «окружающий» свет, рассеянный от неба. Для этого вам необходимо понять, какая область неба видна из каждой точки на поверхности каждого объекта. Эта область уменьшается (например), когда большой объект приближается к рассматриваемой нами точке, поэтому мы не можем просто вычислить полный телесный угол неба, который виден, — нам необходимо знать, какие части — форму неба, видимую из этой точки. Описание этой «формы неба» — это функция на воображаемой сфере, окружающей эту точку. Однако ПОЛНОЕ описание этой формы потребовало бы безумно большого количества данных в каждой точке на поверхности каждого объекта... но сферические гармоники позволяют нам аппроксимировать эту форму, используя гораздо меньше данных. Математика в действии! SteveBaker ( обсуждение ) 02:25, 4 мая 2009 (UTC) [ ответ ]

Это действительно круто! Спасибо. Может быть, у нас будет пара изображений - одно с 3D компьютерной графикой, а может быть, еще одно с магнитным полем Марса или что-то в этом роде. Awickert ( talk ) 06:27, 4 мая 2009 (UTC) [ ответить ]

Я изменился

${\displaystyle \nabla ^{2}Y_{\ell }^{m}(\theta ,\varphi )=-\ell (\ell +1)Y_{\ell }^{m}(\theta ,\varphi )}$

в

${\displaystyle \nabla ^{2}Y_{\ell }^{m}(\theta ,\varphi )=-{\frac {\ell (\ell +1)}{r^{2}}}Y_{\ell }^{m}(\theta ,\varphi )}$, потому что я предполагаю, что : относится к : , в противном случае мы могли бы назвать это : , так что : , что сделало бы это намного менее двусмысленным. В любом случае, я думаю, что уравнение в том виде, в котором оно было, неверно.${\displaystyle \nabla ^{2}}$${\displaystyle \Delta f(r,\vartheta ,\phi )={\frac {1}{r^{2}}}{\frac {\partial }{\partial r}}\left(r^{2}\cdot {\frac {\partial f}{\partial r}}\right)+{\frac {1}{r^{2}\sin \vartheta }}\cdot {\frac {\partial }{\partial \vartheta }}\left(\sin \vartheta \cdot {\frac {\partial f}{\partial \vartheta }}\right)+{\frac {1}{r^{2}\sin ^{2}\vartheta }}\cdot {\frac {\partial ^{2}f}{\partial \phi ^{2}}}}$${\displaystyle \Delta _{\vartheta ,\varphi }}$${\displaystyle \Delta =\Delta _{r}+{\frac {1}{r^{2}}}\Delta _{\vartheta ,\varphi }}$

Кто убрал эту поправку?! Текущая формулировка «на единичной сфере» просто недостаточна. Может случиться, что люди просто найдут уравнение и используют его для расчета без важного множителя . На самом деле, это произошло со мной, и мне потребовалось довольно много времени, чтобы найти ошибку.${\displaystyle {\frac {1}{r^{2}}}}$

Я думаю, что в этой строке есть еще одна проблема (и мне потребовалось довольно много времени, чтобы понять, что было сделано и что пошло не так). Уравнение

${\displaystyle r^{2}\nabla ^{2}Y_{\ell }^{m}(\theta ,\varphi )=-\ell (\ell +1)Y_{\ell }^{m}(\theta ,\varphi ).}$

заставил меня думать, что двойная набла относится к стандартному лапласиану, чего нет. Я думаю, уравнение стало бы правильным, если бы кто-то написал вместо этого, определив его аналогично тому, как определил его человек выше в этом посте.${\displaystyle \Delta _{\theta ,\varphi }}$

Почему «Сферические гармоники» перенаправляют на «Сферические гармоники»? — Предыдущий неподписанный комментарий добавлен 76.185.73.179 ( обсуждение ) 05:38, 12 июля 2009 (UTC) [ ответить ]

Введение утверждает, что сферические гармоники являются набором решений лапласиана. Однако, это не решения, а собственные функции (см. обсуждение выше или см. http://en.wikipedia.org/wiki/Laplace_operator ). Я нахожу это очень вводящим в заблуждение... -- Nbonneel (обсуждение) 12:36, 20 июля 2009 (UTC) [ ответить ]

EDIT: Я понял, что это решение уравнения Лапласа. Утверждение " является угловой частью множества решений уравнения Лапласа" таким образом верно. Однако тот факт, что они являются собственными функциями угловой части лапласиана, кажется еще более интересным для сообщения во введении... -- Nbonneel (обсуждение) 17:23, 24 июля 2009 (UTC) [ ответить ]${\displaystyle r^{l}.Y_{l}^{m}}$${\displaystyle Y_{l}^{m}}$

Ну, они оба, не так ли? "Решения уравнения Лапласа" - это классический (т.е. 19-го века) способ думать о них. Однако я согласен, что подход "собственных функций" немного недооценен во вступительном абзаце. 173.75.156.204 (обсуждение) 01:11, 21 октября 2009 (UTC) [ ответить ]

В

он говорит

Рассмотрим задачу нахождения решений вида ƒ ( r ,θ,φ) =  r ⁿ Θ(θ)Φ(φ), где n — неотрицательное целое число .

далее следует сноска:

В общем случае можно рассматривать решения вида R ( r )Θ(θ)Φ(φ) и выводить вид R из вида Θ, решая впоследствии уравнение Штурма-Лиувилля с соответствующими граничными условиями, но предположение, что R имеет требуемый вид заранее, упрощает изложение.

Решения с n как отрицательным целым числом также присутствуют, и эти функции, которые стремятся к нулю, когда r стремится к бесконечности, очень важны в математической физике. Фактически, в общем случае только эти решения с отрицательным n полезны в физике!

Stamcose ( обсуждение ) 11:33, 24 декабря 2009 (UTC) [ ответить ]

Несколько замечаний. Во-первых, (поверхностные) сферические гармоники, полученные с помощью отрицательной однородности, идентичны тем, которые получены для положительной однородности. Во-вторых, отрицательные однородные решения не получаются из решения той же самой задачи на собственные значения Штурма-Лиувилля, поскольку они, очевидно, нерегулярны при r  = 0. Вместо этого вам нужно решить проблему, которая возникает из предположения о затухании на бесконечности. Очевидно, учитывая, что два подхода в конечном итоге дают идентичные результаты, это дело вкуса, какой из этих подходов вы хотите использовать. Для меня, по крайней мере, более понятно иметь хорошие функции, которые не взрываются. В-третьих, трактовка здесь взята из Методов математической физики Куранта и Гильберта , которые являются очень авторитетным современным источником двух ведущих математических физиков первой половины двадцатого века. Славомир Бялы ( обсуждение ) 12:51, 24 декабря 2009 (UTC) [ ответ ]

Для меня Курант-Гильберт тоже любимый. Тем не менее, в физике я встречаю только те, которые стремятся к нулю в бесконечности!

Но у меня есть еще один комментарий:

Применяя подход в общем случае, приходим к дифференциальному уравнению ${\displaystyle R(r)}$

${\displaystyle {\frac {d}{dr}}\left(r^{2}{\frac {dR}{dr}}\right)=\lambda R}$

с общим решением

${\displaystyle c_{1}r^{l_{1}}+c_{2}r^{l_{2}}}$

где и — константы интегрирования, а и — два решения уравнения${\displaystyle c_{1}}$${\displaystyle c_{1}}$${\displaystyle l_{1}}$${\displaystyle l_{2}}$

${\displaystyle l\,(l+1)=\lambda }$

1) Это не имеет никакого отношения к «Штурму-Лиувиллю», связь с «Штурмом-Лиувиллем» появляется позже в анализе.

2) Здесь ограничиваются целыми значениями , т.е. только теми, которые имеют вид , далее рассматриваются${\displaystyle l}$${\displaystyle \lambda }$${\displaystyle \lambda =l\,(l+1)}$

3) В математической физике обычно интересуют только отрицательные значения целых чисел (т.е. то, о чем уже говорилось).${\displaystyle l}$

Stamcose ( обсуждение ) 13:50, 24 декабря 2009 (UTC) [ ответить ]

(1)-(2) Что ж, вы не получите от меня никаких аргументов, что это общее решение уравнения (кстати, уравнения Штурма-Лиувилля, независимо от того, хотим ли мы притворяться иначе). Однако Штурм-Лиувилль используется для обоснования сосредоточения внимания на решениях рассматриваемой формы (с неотрицательным целым показателем), поскольку это единственные решения, которые являются регулярными в начале координат. _{Вычеркнут, потому что именно регулярность Θ, а не R , дает форму собственного значения.} В тексте мы только что предположили, что решение имеет требуемую форму заранее. Цель сноски - указать, что это предположение обосновано, не вдаваясь в подробности обоснования, но, по-видимому, эта цель неясна, поскольку она привела к вышеуказанному недоразумению. Возможно, лучше включить больше подробностей в сноску. Это удовлетворит ваши возражения? (3) Есть ли у вас какая-либо ссылка, указывающая на то, что интересуют только сферические гармоники для отрицательных значений ? Это, конечно, не согласуется с большинством трактовок сферических гармоник, которые я видел (включая Куранта и Гильберта). Таблицы сферических гармоник всегда имеют . Я также должен сказать, что согласен с тем, что многие физики в первую очередь интересуются нерегулярными сплошными гармониками для таких вещей, как мультипольные разложения, но поверхностные гармоники в обоих случаях совершенно одинаковы. В математике сферическая гармоника — это гармонический однородный многочлен (в любой размерности). Настоящая статья имеет то достоинство, что соглашается с этим соглашением, и, похоже, оно поддерживается большинством доступной литературы. Sławomir Biały ( talk ) 14:24, 24 декабря 2009 (UTC) [ ответить ]${\displaystyle Y_{\ell }^{m}}$${\displaystyle \ell }$${\displaystyle \ell =0,1,2,...}$

Хорошо, я включил почти все детали. Я не считаю, что это сильно улучшает читаемость (особенно для тех, кто еще не знаком с теорией), но, по крайней мере, это должно подкрепить любые возражения против текста. Sławomir Biały ( talk ) 16:00, 24 декабря 2009 (UTC) [ ответить ]

Я все еще не полностью доволен текстом.

1)

${\displaystyle {\frac {1}{\Phi (\varphi )}}{\frac {d^{2}\Phi (\varphi )}{d\varphi ^{2}}}=-m^{2}}$

Почему  ?${\displaystyle \ -m^{2}}$

Необходимо написать общее аналитическое решение линейного дифференциального уравнения второго порядка и четко объяснить, что только при

${\displaystyle {\frac {1}{\Phi (\varphi )}}{\frac {d^{2}\Phi (\varphi )}{d\varphi ^{2}}}=-\mu }$где для целого числа m это уникальная функция в трехмерном пространстве, определенная в сферических координатах.${\displaystyle \mu =m^{2}}$

2) Аргумент, почему параметр λ должен иметь вид λ = ℓ(ℓ+1) для некоторого целого числа ℓ, также не ясен из текста. Аргумент должен исходить из анализа . ${\displaystyle R(r)}$

3) Это не задача Штурма–Лиувилля , которая заставляет параметр λ иметь вид λ = ℓ(ℓ+1) для некоторого целого ℓ. Задача Штурма–Лиувилля является решением дифференциального уравнения для полинома Лежандра (см. эту статью!)

Stamcose ( обсуждение ) 22:57, 24 декабря 2009 (UTC) [ ответить ]

1) См. основную теорему алгебры . 2) Причина в регулярности Θ. Это не имеет ничего общего с R (если только мы не наложим регулярность в начале координат, что мы тогда и сделаем, но не потому, что это даст форму λ). 3) Да, это классическая задача Штурма-Лиувилля на собственные значения: наложение регулярности решений в граничных значениях. Я сейчас не дома, позже смогу дать точные ссылки. Sławomir Biały ( talk ) 23:34, 24 декабря 2009 (UTC) [ ответить ]

Я теперь приложил все усилия, чтобы обеспечить точное соответствие содержания цитируемому источнику (Курант и Гильберт). К сожалению, теперь он также включает в себя довольно много деталей, которых я хотел избежать, но это, казалось, было необходимо, учитывая вышеупомянутые разногласия и путаницу. Я надеюсь, что все это урегулирует некоторые из проблем, на которые вы указали. Спасибо, Славомир Бялы ( talk ) 16:27, 25 декабря 2009 (UTC) [ ответить ]

++++++++++++++++++

Я бы предложил такой текст. Он гораздо более подробный и явный, и поэтому, на мой взгляд, более удобный для пользователя Википедии, чем Курант-Гильберт, который адресован профессиональным математикам.

Уравнение Лапласа в сферических координатах имеет вид:

${\displaystyle \nabla ^{2}f={1 \over r^{2}}{\partial \over \partial r}\left(r^{2}{\partial f \over \partial r}\right)+{1 \over r^{2}\sin \theta }{\partial \over \partial \theta }\left(\sin \theta {\partial f \over \partial \theta }\right)+{1 \over r^{2}\sin ^{2}\theta }{\partial ^{2}f \over \partial \varphi ^{2}}=0}$

(см. также del в цилиндрических и сферических координатах ). Рассмотрим задачу нахождения решений вида ƒ ( r ,θ,φ) =  R ( r )Θ(θ)Φ(φ). Разделением переменных получаются два дифференциальных уравнения, наложенные на уравнение Лапласа:

${\displaystyle {\frac {1}{R}}{\frac {d}{dr}}\left(r^{2}{\frac {dR}{dr}}\right)=\lambda ,\qquad {\frac {1}{\Theta \sin \theta }}{\frac {d}{d\theta }}\left(\sin \theta {\frac {d\Theta }{d\theta }}\right)+{\frac {1}{\Phi \sin ^{2}\theta }}{\frac {d^{2}\Phi }{d\varphi ^{2}}}=-\lambda }$

где λ — константа.

Первое из этих уравнений имеет вид

${\displaystyle {\frac {d}{dr}}\left(r^{2}{\frac {dR}{dr}}\right)=\lambda R}$

т.е. это регулярное дифференциальное уравнение второго порядка. При заданных начальных значениях для функции и для ее производной на некотором радиусе это дифференциальное уравнение однозначно определяет значение для любого${\displaystyle R}$${\displaystyle {\frac {dR}{dr}}}$${\displaystyle r=r_{0}}$${\displaystyle R(r)}$${\displaystyle r}$

Функция

${\displaystyle r^{l}}$

является решением этого дифференциального уравнения тогда и только тогда, когда

${\displaystyle l\,(l+1)=\lambda }$

Для любого это уравнение имеет два решения и функцию${\displaystyle \lambda >-{\frac {1}{4}}}$${\displaystyle l_{1},l_{2}}$

${\displaystyle R(r)=c_{1}r^{l_{1}}+c_{2}r^{l_{2}}}$

то удовлетворяет дифференциальному уравнению для любых констант . При любых значениях функции и ее производной на заданном радиусе константы могут быть выбраны так, чтобы соответствовать этим начальным значениям, т.е. общая форма решения найдена.${\displaystyle c_{1},c_{2}}$${\displaystyle R\,\,}$${\displaystyle {\frac {dR}{dr}}\,\,}$${\displaystyle r=r_{0}\,}$${\displaystyle c_{1},c_{2}}$

Далее мы будем рассматривать только целые значения (положительные и отрицательные!) для в и, следовательно, только для целых значений , т.е. для . Каждому значению соответствует одно отрицательное и одно положительное значение для , например, соответствует как и . При одном имеет , стремящийся к бесконечности, когда r стремится к бесконечности, при одном имеет сингулярность при .${\displaystyle l}$${\displaystyle r^{l}}$${\displaystyle \lambda =l\,(l+1)}$${\displaystyle l}$${\displaystyle \lambda =1,2,6,...}$${\displaystyle \lambda }$${\displaystyle l}$${\displaystyle \lambda =2}$${\displaystyle l=-2}$${\displaystyle l=1}$${\displaystyle l\geq 1}$${\displaystyle R(r)}$${\displaystyle l\leq -1}$${\displaystyle r=0}$

Повторное применение разделения переменных ко второму уравнению приводит к паре дифференциальных уравнений

${\displaystyle {\frac {1}{\Phi (\varphi )}}{\frac {d^{2}\Phi (\varphi )}{d\varphi ^{2}}}=-\mu }$

${\displaystyle l\,(l+1)\sin ^{2}(\theta )+{\frac {\sin(\theta )}{\Theta (\theta )}}{\frac {d}{d\theta }}\left[\sin(\theta ){\frac {d\Theta }{d\theta }}\right]=\mu }$

для некоторого целого числа l . Поскольку мы ищем непрерывную и дифференцируемую функцию, удовлетворяющую уравнению Лапласа в 3-мерном пространстве, априори ясно, что она должна быть периодической с периодом . А если не является постоянной, то должна быть равна нулю для и для , в противном случае на полярной оси сферической системы координат будет сингулярность.${\displaystyle \Phi (\varphi )}$${\displaystyle 2\pi }$${\displaystyle \Phi (\varphi )}$${\displaystyle \Theta (\theta )}$${\displaystyle \theta =0}$${\displaystyle \theta =2\pi }$

Первое из двух уравнений принимает вид

${\displaystyle {\frac {d^{2}\Phi (\varphi )}{d\varphi ^{2}}}=-\mu \Phi (\varphi )}$

Это линейное дифференциальное уравнение второго порядка с постоянными коэффициентами имеет периодическое решение с периодом тогда и только тогда, когда для целого числа , в этом случае общее решение имеет вид${\displaystyle 2\pi }$${\displaystyle \mu =m^{2}}$${\displaystyle m}$

${\displaystyle \Phi (\varphi =A\cos(m\phi )+B\sin(m\phi )}$

где константы.${\displaystyle A,\,B}$

Второе уравнение имеет вид:

${\displaystyle {\frac {1}{\sin(\theta )}}{\frac {d}{d\theta }}\left[\sin(\theta ){\frac {d\Theta }{d\theta }}\right]+\left[l\,(l+1)-{\frac {m^{2}}{\sin ^{2}(\theta )}}\right]\Theta (\theta )=0}$

и после подстановки переменных читается${\displaystyle x=\cos(\theta )}$

${\displaystyle {\frac {d}{dx}}\left[(1-x^{2}){\frac {d}{dx}}\Theta (x)\right]+\left[l(l+1)-{\frac {m^{2}}{1-x^{2}}}\right]\Theta (x)=0}$

Это дифференциальное уравнение Штурма-Лиувилля . Для , т.е. для случая, который является константой, это дифференциальное уравнение, решениями которого являются полиномы Лежандра . Если это дифференциальное уравнение, решениями которого являются ассоциированные функции Лежандра .${\displaystyle m=0}$${\displaystyle \Phi (\phi )}$${\displaystyle m\geq 1}$

Первые несколько полиномов Лежандра:

л	${\displaystyle P_{l}(x)\,}$
0	${\displaystyle 1\,}$
1	${\displaystyle x\,}$
2	${\displaystyle {\begin{matrix}{\frac {1}{2}}\end{matrix}}(3x^{2}-1)\,}$
3	${\displaystyle {\begin{matrix}{\frac {1}{2}}\end{matrix}}(5x^{3}-3x)\,}$
4	${\displaystyle {\begin{matrix}{\frac {1}{8}}\end{matrix}}(35x^{4}-30x^{2}+3)\,}$
5	${\displaystyle {\begin{matrix}{\frac {1}{8}}\end{matrix}}(63x^{5}-70x^{3}+15x)\,}$
6	${\displaystyle {\begin{matrix}{\frac {1}{16}}\end{matrix}}(231x^{6}-315x^{4}+105x^{2}-5)\,}$
7	${\displaystyle {\begin{matrix}{\frac {1}{16}}\end{matrix}}(429x^{7}-693x^{5}+315x^{3}-35x)\,}$
8	${\displaystyle {\begin{matrix}{\frac {1}{128}}\end{matrix}}(6435x^{8}-12012x^{6}+6930x^{4}-1260x^{2}+35)\,}$
9	${\displaystyle {\begin{matrix}{\frac {1}{128}}\end{matrix}}(12155x^{9}-25740x^{7}+18018x^{5}-4620x^{3}+315x)\,}$
10	${\displaystyle {\begin{matrix}{\frac {1}{256}}\end{matrix}}(46189x^{10}-109395x^{8}+90090x^{6}-30030x^{4}+3465x^{2}-63)\,}$

Коэффициент масштабирования по соглашению выбирается таким образом, чтобы абсолютное значение полиномов Лежандра принимало значение 1 при x=-1 и x=1.

Сферические гармоники, соответствующие${\displaystyle l=-3\,,\,\lambda =6\,,\,m=0}$

${\displaystyle {\frac {P_{2}(cos(\theta ))}{r^{3}}}={\frac {1}{r^{3}}}{\frac {1}{2}}(3\cos ^{2}-1)}$

В прямоугольной системе координат эта гармоника принимает вид

${\displaystyle {\frac {1}{r^{5}}}{\frac {1}{2}}(3z^{2}-r^{2})}$

Первые несколько связанных функций Лежандра :${\displaystyle P_{l}^{m}}$

${\displaystyle P_{1}^{1}(x)=-(1-x^{2})^{1/2}}$

${\displaystyle P_{2}^{1}(x)=-3x(1-x^{2})^{1/2}}$

${\displaystyle P_{2}^{2}(x)=3(1-x^{2})}$

${\displaystyle P_{3}^{1}(x)=-{\begin{matrix}{\frac {3}{2}}\end{matrix}}(5x^{2}-1)(1-x^{2})^{1/2}}$

${\displaystyle P_{3}^{2}(x)=15x(1-x^{2})}$

${\displaystyle P_{3}^{3}(x)=-15(1-x^{2})^{3/2}}$

${\displaystyle P_{4}^{1}(x)=-{\begin{matrix}{\frac {5}{2}}\end{matrix}}(7x^{3}-3x)(1-x^{2})^{1/2}}$

${\displaystyle P_{4}^{2}(x)={\begin{matrix}{\frac {15}{2}}\end{matrix}}(7x^{2}-1)(1-x^{2})}$

${\displaystyle P_{4}^{3}(x)=-105x(1-x^{2})^{3/2}}$

${\displaystyle P_{4}^{4}(x)=105(1-x^{2})^{2}}$

Все эти связанные функции Лежандра имеют то, что является предпосылкой для функции ${\displaystyle P_{l}^{m}(-1)=P_{l}^{m}(1)=0}$

${\displaystyle R(r)\Theta (\theta )\Phi (\phi )}$

быть непрерывным и дифференцируемым на полярной оси сферической системы координат

В качестве примера, для и для двух сферических гармоник${\displaystyle l=-3}$${\displaystyle m=1}$

${\displaystyle {\frac {1}{r^{3}}}3\cos(\theta )\sin(\theta )\cos(\phi )}$

${\displaystyle {\frac {1}{r^{3}}}3\cos(\theta )\sin(\theta )\sin(\phi )}$

Используя прямоугольные координаты, они

${\displaystyle {\frac {1}{r^{5}}}3zx}$

${\displaystyle {\frac {1}{r^{5}}}3zy}$

т.е. они непрерывны и дифференцируемы всюду, за исключением сингулярности в точке${\displaystyle r=0}$

Stamcose ( обсуждение ) 20:58, 25 декабря 2009 (UTC) [ ответить ]

Я не согласен с предлагаемой редакцией. Версия в статье согласуется с Курантом и Гильбертом, из которых она в настоящее время взята. Если есть другие источники такого же высокого качества, которые делают вещи похожим образом, то мы можем обсудить достоинства. Однако, как я уже указал, радиальное уравнение имеет лишь периферийное значение. Сферические гармоники являются собственными функциями угловой части Лапласа, что определенно требует решения нетривиальной задачи на собственные значения (см. связанную функцию Лежандра ). Более того, предлагаемая редакция не объясняет, почему l должно быть целым числом, что, по-видимому, является серьезным ограничением, учитывая, что первоначальное возражение состояло в том, что статья не смогла объяснить именно этот момент. Кроме того, здесь не место для длинных таблиц твердых сферических гармоник. У нас есть твердые сферические гармоники и таблица сферических гармоник для таких вещей. Наконец, я также в целом не согласен с тем, что использование сплошных гармоник с отрицательной однородностью улучшает представление, но в любом случае я уже сказал, что радиальная часть является периферийной, и теперь есть сноска к статье, объясняющая различные соглашения. Славомир Бялы ( обсуждение ) 22:26, ​​25 декабря 2009 (UTC) [ ответ ]

Также я заметил, что разделение переменных никогда не оправдано. Поэтому предлагаемая редакция также не дает никаких указаний на то, почему радиальные собственные функции охватываются сферическими гармониками Лапласа . Sławomir Biały ( talk ) 22:36, 25 декабря 2009 (UTC) [ ответить ]${\displaystyle Y_{\ell }^{m}}$

В настоящем тексте говорится:

${\displaystyle {\frac {1}{\Phi (\varphi )}}{\frac {d^{2}\Phi (\varphi )}{d\varphi ^{2}}}=-m^{2}}$

а потом

Априори m является комплексной константой, но поскольку Φ должна быть периодической функцией , период которой нацело делит 2π,

Нет смысла усложнять вещи с комплексными числами. Гармонические функции — это функции в . И общее решение дифференциального уравнения ${\displaystyle R^{3}}$

${\displaystyle {\frac {d^{2}\Phi (\varphi )}{d\varphi ^{2}}}=-\mu \Phi (\varphi )}$

для положительных и отрицательных хорошо известно из школьной математики без использования комплексных чисел${\displaystyle \mu }$

В настоящем тексте говорится:

Наложение этой закономерности на Θ в граничных точках области представляет собой задачу Штурма–Лиувилля , которая заставляет параметр λ иметь вид λ = ℓ(ℓ+1) для некоторого неотрицательного целого числа с ℓ ≥ | m |.

Это просто неверно, как я уже писал несколько раз.

То, что λ имеет вид λ = ℓ(ℓ+1) для некоторого неотрицательного целого числа, должно быть (ℓ ≥  m, поскольку m по определению больше или равно 0) . Вместо этого следует из дифференциального уравнения

${\displaystyle {\frac {d}{dr}}\left(r^{2}{\frac {dR}{dr}}\right)=\lambda R}$

как я пишу в правильной версии! Не имеет ничего общего с проблемой Штурма–Лиувилля !

Вероятно, лучше использовать условное обозначение, что является неотрицательным целым числом, но при этом подчеркнуть, что оба значения и являются одинаково допустимыми.${\displaystyle l}$${\displaystyle R=r^{l}}$${\displaystyle R={\frac {1}{r^{l+1}}}}$

Не вдаваясь в эти подробности, я также не убежден в остальном тексте. Этот материал достаточно сложен для читателя, даже с абсолютно ясным и правильным текстом. И я думаю, важно, чтобы были представлены некоторые конкретные примеры сферических гармоник, чтобы сделать вопрос менее абстрактным.

Stamcose ( обсуждение ) 11:29, 26 декабря 2009 (UTC) [ ответить ]

Извините, но я снова не согласен. Во-первых, «не нужно усложнять вещи с комплексными числами» кажется странным советом, учитывая, что решения в любом случае являются сложными экспоненциальными функциями, и в статье об этом говорится в следующем предложении. В любом случае, я изменил текст на этот в качестве примирительного жеста, потому что вы предположили, что есть некоторая проблема с записью числа m ² ; но мне кажется, что введение новой константы только для того, чтобы сослаться на это и тут же от нее отказаться, сложнее, чем просто написать m ² в самом начале (поскольку это, очевидно, возможно). Во-вторых, я вижу, что вы все еще не убеждены, что этот подход правильный и элегантный. Хороший способ достичь решения — это, согласно моему предложению выше, представить надежные источники , которые столь же высокого качества, как и те, которые уже есть в тексте (Курант–Гильберт), в которых вместо этого радиальное уравнение дает правильное собственное значение. Сравнение вашего источника с тем, который привел я, может помочь разрешить наш спор. В-третьих, далее в тексте уже есть примеры сферических гармоник, включая рисунки, иллюстрации их узловых областей и т. д. Нет необходимости дублировать содержание этого отдельного раздела с остальной частью статьи. В-четвертых, относительно вашего убеждения, что «Это просто неверно, как я уже писал несколько раз», вы написали это, и я также ответил на это, но все мои ответы остались без ответа (обсуждение, кажется, одностороннее, как будто мы оба говорили мимо друг друга). Еще раз, Курант и Гильберт — хорошее введение в проблемы Штурма–Лиувилля; они представляют общее уравнение Лежандра как пример именно такого рода проблем ( §V.10. Проблемы типа Штурма–Лиувилля. Особые граничные точки. ). Наконец, последняя версия (которую я призываю вас прочитать и попытаться понять до самого конца) вообще преуменьшает роль радиального уравнения и, по крайней мере, указывает, что оба и являются действительными. Славомир Бялы ( обсуждение ) 13:11, 26 декабря 2009 г. (UTC) [ ответить ]${\displaystyle r^{\ell }}$${\displaystyle r^{-\ell -1}}$

Кажется, во втором уравнении (во второй строке) отсутствует элемент , полученный путем разделения переменных в разделе «Сферические гармоники Лапласа». Добавляем его к уравнению. —Предыдущий комментарий без знака , добавленный Pocav (обсуждение • вклад ) 19:36, 31 января 2010 (UTC) [ ответить ]${\displaystyle {\frac {1}{Y}}}$

Изображение 'Harmoniki.png', показанное в поле в правом верхнем углу статьи, неверно (или, по крайней мере, вводит в заблуждение) — показанные функции не являются линейно независимыми. Например, во втором ряду функций (L=1, похоже на 2p-орбиталь), слева направо, график показывает p_x, p_z, (-p_x), а не p_x, p_z, p_y. [В тригонометрических формулах: sin(theta)cos(phi), cos(theta), -sin(theta)cos(phi), тогда как последняя должна быть sin(theta)sin(phi)] —Предыдущий комментарий без знака добавлен Gingekerr ( обсуждение • вклад ) 15:20, 16 ноября 2010 (UTC) [ ответить ]

Хороший момент. Кто-нибудь должен это исправить. Похоже, тот, кто создал изображение, использовал неправильный поворот. Sławomir Biały ( talk ) 16:11, 16 ноября 2010 (UTC) [ ответить ]

Более того, это изображение используется как для сферической, так и для кубической гармоники, что, как я предполагаю, не должно быть одним и тем же. — Parsa ( обсуждение ) 01:20, 23 сентября 2011 (UTC) [ ответить ]

Статья кубические гармоники очень плохая. В ней говорится, что кубическая гармоника — это сферическая гармоника, умноженная на «радиальную часть волновой функции», но нигде не говорится, чему равна радиальная часть волновой функции. Я думаю, что это то же самое, что и сплошные сферические гармоники , но, возможно, я ошибаюсь. В любом случае, мне ясно, что эти изображения определенно не являются точными визуальными изображениями кубических гармоник. Кубические гармоники — это функции в пространстве (т. е. функции трех переменных), а не просто функции на сфере. Эти изображения — графики функций на сфере, где цвет обозначает знак. Sławomir Biały ( talk ) 12:45, 23 сентября 2011 (UTC) [ ответить ]

Я добавил несколько комментариев в File_talk:Harmoniki.png . Изображение в начале прекрасное, и его можно легко исправить. Есть ли у кого-нибудь исходный код? 70.116.95.66 ( talk ) 00:40, 15 апреля 2013 (UTC) [ ответить ]

Я удалил шаблон из раздела внешних ссылок, который не был подкреплен никаким обсуждением того, почему внешние ссылки были либо неуместными, либо чрезмерными. Редактору, использующему такой шаблон, настоятельно рекомендуется подкреплять свои возражения соответствующим обсуждением, которое может привести к улучшению статьи. В противном случае он/она просто добавляет шума. Dlw20070716 ( talk ) 18:28, 15 июля 2011 (UTC) [ ответить ]

Хороший момент. Я удалил внешние ссылки из статьи, так как они, похоже, добавляют ненужный шум. Пожалуйста, восстановите их по отдельности, если вы считаете, что ссылка добавляет ценность и соответствует WP:ELNO . Вот список ссылок. Всего наилучшего, Sławomir Biały ( talk ) 19:03, 15 июля 2011 (UTC) [ ответить ]

• Интерактивный калькулятор сферических гармоник на домашней странице исследований Тала Кармона
• Сферические гармоники, применяемые для анализа акустического поля на странице исследований Trinnov Audio
• Сферические гармоники Стивена Вольфрама и узловые области сферических гармоник Майкла Тротта, проект демонстраций Вольфрама
• Доступное введение в сферические гармоники (Дж. Б. Калверт)
• Citizendium:Сферические гармоники
• Демонстрация сферических гармоник OpenGL
• Анимации сферических гармоник Аллена Макнамары
• Анимации сферических гармоник Торстена Беккера

Программное обеспечение

• Генератор сферических гармоник в OpenGL
• SHTOOLS: архив программного обеспечения Fortran 95
• HEALPIX: архив программного обеспечения Fortran 90 и C++
• SpherePack: архив программного обеспечения Fortran 77
• SpharmonicKit: архив программного обеспечения на языке C
• Фредерик Дж. Саймонс: Архив программного обеспечения Matlab
• NFFT: библиотека подпрограмм C (быстрое сферическое преобразование Фурье для произвольных узлов)
• Shansyn: пакет сферических гармоник для файлов GMT/netcdf grd
• SHAPE: Сферический гармонический параметризатор Explorer

Не понимаю, почему вы удалили программное обеспечение и другие ссылки. Они очень полезны для меня и могут быть полезны для других.--Mikeev ( talk ) 12:44, 26 октября 2011 (UTC) [ ответить ]

Wikipedia — это не ферма ссылок. Обычно мы не должны включать ссылки на программное обеспечение, если статья не посвящена конкретно программному пакету. В сети есть и другие опубликованные списки соответствующих программных пакетов, но это не наша работа. Что касается остальных, то это в основном личные веб-сайты людей или сайты, не имеющие какой-либо экспертной оценки, и поэтому также имеющие сомнительную ценность для такой энциклопедии, как эта. Энциклопедические внешние ссылки, конечно, уместны. Sławomir Biały ( talk ) 12:02, 3 ноября 2011 (UTC) [ ответить ]

Я думаю, что в этом уравнении

${\displaystyle {\frac {1}{4\,\pi }}\int _{\Omega }f(\Omega )^{2}\,d\Omega =\sum _{\ell =0}^{\infty }S_{f\!f}(\ell ),}$

фактор

${\displaystyle {\frac {1}{4\,\pi }}}$

следует исключить, учитывая нормализацию, принятую для сферических гармоник, или вместо этого добавить в

${\displaystyle S_{f\!f}(\ell )={\frac {1}{4\,\pi }}\sum _{m=-\ell }^{\ell }f_{\ell m}^{2}}$

для согласованности, но это не мое предпочтительное решение. — Предыдущий неподписанный комментарий добавлен F. Mignard (обсуждение • вклад ) 12:56, 18 апреля 2012 (UTC) [ ответить ]

У меня такое чувство, что эта статья просто непонятна тем, кто еще не имеет представления о материале. По моему мнению, в результате статья не особенно полезна. У меня нет предложений относительно того, как это исправить, но это проблема, которую я наблюдаю практически в каждой статье на Википедии, где много математики, и моя точка зрения не является точкой зрения дилетанта. Snrrub (обсуждение) 18:48, 1 мая 2012 (UTC) [ ответить ]

Это правда, что это не совсем вводная статья, но тема сферических гармоник не совсем подходит для вводного рассмотрения в форме энциклопедии. Существует множество учебников и учебных пособий, которые удовлетворяют эту потребность. Sławomir Biały ( talk ) 21:13, 1 мая 2012 (UTC) [ ответить ]

Разве не должна любая энциклопедия все еще быть в состоянии объяснить, что такое что-то любому, кто на это смотрит? У нее даже нет резюме, которое помогло бы большинству людей. Те люди, которые понимают эту статью, уже знают, что такое SH. Это энциклопедия, а не социальный клуб. — Предыдущий неподписанный комментарий добавлен 205.201.101.153 (обсуждение) 17:57, 8 марта 2015 (UTC)[ отвечать ]

Основная цель этой статьи — включить много информации о сферических гармониках. Это, как правило, цель энциклопедии: содержать много информации, обычно организованной в некоторую полезную форму, чтобы исследователи могли затем использовать эту информацию. Я не знаю ни одного социального клуба, для которого это было бы основной целью. Я бы не стал возражать против более вводного отчета (при условии, что он не будет неправильным), но как мог бы выглядеть такой отчет? Сферические гармоники — это угловые части решений уравнения Лапласа. Эквивалентно, они являются собственными состояниями углового момента. Оба они выводятся более или менее из первых принципов во втором разделе статьи, предполагая только знакомство с векторным исчислением. Поэтому утверждение, что в статье отсутствует вводная информация, здесь кажется ленью со стороны читателя. А сравнение статьи с социальным клубом кажется скорее троллингом. Славомир Бялы ( обсуждение ) 22:56, 8 марта 2015 г. (UTC) [ ответить ]

Я попытался сделать свинец немного ниже в начале; если ничего другого, возможно, неискушенный читатель мог бы почерпнуть, что это полезные функции, определенные на сфере. Посмотрим, что вы думаете. -- Марк Викинг ( обсуждение ) 00:00, 9 марта 2015 (UTC) [ ответить ]

Изображение в статье самое запутанное во всей статье, потому что сферические гармоники определены на сфере фиксированного радиуса и, следовательно, не зависят от радиуса, но это изображение создает впечатление, что они являются функциями радиуса. Я предлагаю поменять местами это первое изображение с изображением ниже, которое показывает сферические гармоники на поверхности сферы. 129.63.129.196 ( talk ) 19:38, 11 октября 2012 (UTC) [ reply ]

Если это имеет значение, первое изображение — это визуализация r=Y(φ,θ). Поскольку эта визуализация, по-видимому, имеет другие проблемы (см. предыдущие комментарии; IIRC Я также пытался решить эту проблему на pl:), у меня нет проблем с перенастройкой изображений на этой странице. Хотя я чувствую, что адекватная подпись и, возможно, исправление исходного первого изображения были бы идеальными. Sławomir Biały ( talk ) 00:09, 12 октября 2012 (UTC) [ ответить ]

129.63.129.196 прав, File:Harmoniki.png введет в заблуждение читателя, который не приложил значительных усилий, чтобы понять используемое представление. Рисунки File:Spherical harmonics.png и File:Harmoniques spheriques positif negatif.png в разделе Визуализация сферических гармоник самые наглядные. Однако радиальный график также может быть понятным, если он показывает отклонения малой амплитуды от в основном сферической поверхности.

Анимация File :Rotatingspheric harmonics.gif неплоха, но было бы лучше, если бы она показывала колеблющиеся стоячие волны, а не волны, бегущие по экватору. Даже самый невнимательный читатель мог бы тогда увидеть, что волны были представлены, и это не тот случай, когда сферы просто вращались. --catslash ( talk ) 12:01, 12 октября 2012 (UTC) [ ответить ]

У меня проблема с этим разделом. Там написано:

${\displaystyle \mathbf {L} ^{2}=L_{x}^{2}+L_{y}^{2}+L_{z}^{2}}$

${\displaystyle {\begin{aligned}L_{+}&=L_{x}+iL_{y}\\L_{-}&=L_{x}-iL_{y}\end{aligned}}}$

и

${\displaystyle L_{-}L_{+}=\mathbf {L} ^{2}-L_{z}^{2}-L_{z}}$

но моя математика говорит:

${\displaystyle L_{-}L_{+}=(L_{x}-iL_{y})(L_{x}+iL_{y})=L_{x}^{2}+L_{y}^{2}=\mathbf {L} ^{2}-L_{z}^{2}}$

Так откуда же взялся этот термин ?${\displaystyle -L_{z}}$

Linkato1 ( обсуждение ) 09:22, 19 октября 2012 (UTC) [ ответ ]

Вы это предположили, но это неверно... вы составляете операторы, что не обязательно коммутативно ... см. Каноническое коммутационное соотношение и т. д. и т. п. :-) -- Стив ( обсуждение ) 12:09, 19 октября 2012 (UTC) [ ответить ]${\displaystyle L_{x}L_{y}-L_{y}L_{x}=0}$

Боже, я чувствую себя глупо, но спасибо.Linkato1 ( обсуждение ) 16:00, 19 октября 2012 (UTC) [ ответить ]

Давайте приведем здесь правильный расчет, чтобы другие увидели, как он получен.${\displaystyle L_{-}L_{+}=\mathbf {L} ^{2}-L_{z}^{2}-L_{z}}$

${\displaystyle 2L_{z}=[L_{+},L_{-}]=L_{+}L_{-}-L_{-}L_{+}=(L_{x}+iL_{y})(L_{x}-iL_{y})-(L_{x}-iL_{y})(L_{x}+iL_{y})=L_{x}^{2}-iL_{x}L_{y}+iL_{y}L_{x}+L_{y}^{2}-L_{x}^{2}-iL_{x}L_{y}+iL_{y}L_{x}-L_{y}^{2}}$

${\displaystyle =-2iL_{x}L_{y}+2iL_{y}L_{x})=-2i(L_{x}L_{y}-L_{y}L_{x})}$

${\displaystyle =>i(L_{x}L_{y}-L_{y}L_{x})=-L_{z}}$

${\displaystyle L_{-}L_{+}=(L_{x}-iL_{y})(L_{x}+iL_{y})=L_{x}^{2}+iL_{x}L_{y}-iL_{y}L_{x}+L_{y}^{2}}$

${\displaystyle =\mathbf {L} ^{2}-L_{z}^{2}+i(L_{x}L_{y}-L_{y}L_{x})=\mathbf {L} ^{2}-L_{z}^{2}-L_{z}}$

Linkato1 ( обсуждение ) 09:47, 20 октября 2012 (UTC) [ ответ ]

Может быть, можно написать «Подробный вывод см. в разделе Оператор лестницы#Угловой момент — Стив ( обсуждение ) 14:00, 20 октября 2012 (UTC) [ ответить ]

Кажется, что-то не так в выражении для действительных сферических гармоник, записанном в терминах полиномов Лежандра: для отрицательных m я получаю другой результат по сравнению с определением, основанным на Y_l^m. Я предполагаю, что порядок полинома Лежандра должен быть m (а не Abs[m]) в определении действительных сферических гармоник для отрицательных m.

Для положительных m результат тот же и согласуется с комплексными сферическими гармониками.

JiriVejrazka (обсуждение) 10:28, 10 июля 2014 (UTC) [ ответить ]

Я не знаю, согласен ли кто-то еще, но лично мне было бы интересно увидеть раздел, перечисляющий конкретные применения сферических гармоник в различных областях. Например: я видел несколько похожих диаграмм, используемых в звукозаписи (для объяснения методов записи XY и mid-side) и в антенных решетках для дальнего радиовещания ( формирование луча ). Это также кажется применимым к проектированию музыкальных инструментов, например, для более высоких, не- резонансных резонансов Гельмгольца гармоник окарины (см. стр. 4 статьи Дэниела А. Рассела "Баскетбольные мячи как сферические акустические полости", чтобы увидеть некоторые знакомые диаграммы, и "Размер отверстия в сферическом резонаторе" Джареда Кернса).

В качестве альтернативы, если кто-то знает хороший обзор этих различных приложений, пожалуйста, оставьте ссылку здесь. Esn ( talk ) 02:55, 31 декабря 2016 (UTC) [ ответить ]

Было бы полезно включить хотя бы один рисунок, показывающий визуализацию сложных (а не реальных) сферических гармоник. Сложную фазу можно визуализировать как на цветовом круге, в то время как амплитуду можно визуализировать как насыщенность или яркость. Тогда можно получить представление о геометрических сходствах/различиях между сложными и реальными сферическими гармониками. Я исхожу из этого как физик, интересующийся атомными орбиталями в настоящее время. Есть небольшое разъяснение, которое можно было бы сделать о сложных и реальных атомных орбиталях на этой странице: Atomic_orbital#Complex_orbitals , которому могло бы помочь большее распознавание/визуализация сложных сферических гармоник здесь.

Jagerber (обсуждение) 05:21, 17 июля 2018 (UTC) [ ответить ]

Я добавил множество визуализаций для действительных и комплексных сферических гармоник в Таблицу сферических гармоник . Twistar48 ( обсуждение ) 09:46, 5 ноября 2021 (UTC) [ ответить ]

Термин Tesseral Harmonics перенаправляет на страницу Spherical Harmonics, тогда как Cubic Harmonics имеет свою собственную дополнительную страницу. Страница на сайте Cubic Harmonics не обсуждает собственные состояния кубической симметрии, но обсуждает Tesseral Harmonics. Я бы предложил создать отдельную страницу для Tesseral Harmonics и Cubic Harmonics и готов заполнить их. (Это приведет к той же структуре, что и на немецком сайте Wiki)

Мауриц В. Хаверкорт (обсуждение) 08:23, 21 мая 2020 г. (UTC) [ ответить ]

На этой странице было довольно много дополнений. VerifyTruth01 (обсуждение) 20:44, 9 августа 2024 (UTC) [ ответить ]

Введение содержит следующее предложение:

« Поскольку сферические гармоники образуют полный набор ортогональных функций и, таким образом, ортонормированный базис, каждая функция, определенная на поверхности сферы, может быть записана в виде суммы этих сферических гармоник » .

Бессмысленно упоминать ортонормированный базис без малейшего намека на то, что это за ортонормированный базис .

Надеюсь, кто-нибудь сможет добавить эту информацию, тем самым значительно улучшив введение.

— Предыдущий неподписанный комментарий добавлен 2601:204:f181:9410:10ad:61e0:72e5:372d ( обсуждение ) 22:45, 9 декабря 2024 (UTC) [ ответ ]

Базис пространства функций, определенных на сфере. – jacobolus  (t) 23:06, 9 декабря 2024 (UTC) [ ответить ]